静态障碍物下的遍历多任务目标机器人路径规划
2018-09-18薛亚冲
杨 帆 ,薛亚冲 ,李 靖
(1.河北工业大学 电子信息工程学院,天津 300400;2.河北工业大学 天津市电子材料与器件重点实验室,天津 300400)
针对移动机器人导航技术的研究是移动机器人研究领域的核心,而路径规划是机器人导航技术中的研究热点[1].机器人路径规划的目的是为机器人规划出一条从起始点至目标点的最优或近似最优的行走路径[2].目前,机器人路径规划的方法有多种,主要可分为全局路径规划和局部路径规划[3],全局路径规划主要包括:栅格法、可视图法和一些神经网络算法[4]等,局部路径规划主要包括:人工势场法、蚁群算法、粒子群算法、遗传算法和A*寻路算法等.而多任务目标点的机器人路径规划相较于单点目标的路径规划要更为复杂.
目前,在机器人路径规划的研究中,大多数是针对单任务目标这一情况,对于多任务目标的研究较少[5].蒲兴成等[2]将反向学习策略思想应用到粒子群算法中,这种改进虽然一定程度上抑制了单个粒子的早熟现象,并且提高了算法收敛速度,但并没有有效解决粒子群算法容易陷入局部最优的弊端,而且算法仿真中没有考虑目标点较多的情况.曹洁等[4]提出了一种改进蚁群算法对捡球机器人进行多目标路径规划,将蚁群算法中信息素强度Q设为动态,这种改进虽然解决了蚁群算法可能出现的停滞现象,且提高了一定的求解精度,但改进后的算法还是容易陷入局部最优,且算法在进行路径规划时没有考虑到障碍物的存在,算法应用范围受到极大限制.针对这些问题,本文提出了一种基于粒子群-遗传-A*算法的静态障碍物下的遍历多任务目标机器人路径规划.在进行路径规划时,首先使用粒子群-遗传算法规划出最优目标点行走顺序,再使用A*算法进行避障行走.该算法将遗传算法中的交叉和变异操作应用到粒子群算法中,显著提高了粒子群算法的稳定性和寻优能力.
1 算法理论基础
1.1 栅格法
采用栅格法构建地图模型,栅格法在构建地图模型时,将障碍物区域即不可行走区域标为1,将自由区域即可行走区域标为0.所构建的地图模型详尽程度取决于划分的栅格大小[5].栅格越小,构建的地图模型越详细,但会占用较大的存储空间,并且会使得路径规划计算量成指数增加,规划速度也会降低[6].栅格过大,会使得地图模型不够详尽,不能准确的描述出障碍区域和自由区域的信息,不利于有效路径的规划.
1.2 A*算法
A*算法是一种启发式搜索算法,在进行路径规划时,A*算法会对将要进行搜索的点预估代价值,代价值预估函数为:

式中:G(n)表示从其实节点到任意节点n的代价;H(n)表示从节点n到目标点的启发式评估代价.
改变G(n)和H(n)的代价值能够调节A*算法的搜索行为,当 G(n)过大,H(n)过小时,A* 算法扩展节点会增多,搜索速度会变慢,但能够规划出一条最优的行走路径;当 G(n)过小,H(n)过大时,A* 算法搜索速度很快,但不能保证规划出的路径为最优.A*算法有2个存储列表:OPEN(开启列表)和CLOSE(关闭列表),OPEN列表中存放等待检查方格,CLOSE列表中存放不需要检查的方格.
A*算法在栅格法构建的地图模型中进行路径规划时,机器人有8个可运动的方向[8],分别为:前方、左方、右方、后方、左前、右前、左后、右后,如图1所示.图1中:A为起始方格;T为目标节点;灰色区域为障碍物区域(在后文的仿真试验中设为蓝色);实线箭头为机器人最佳前进方向.
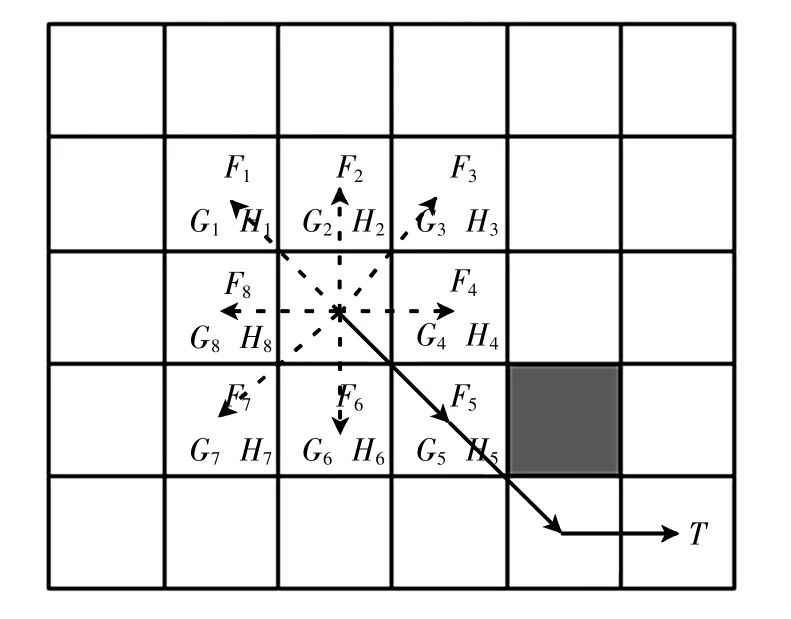
图1 A*算法规划示意图Fig.1 A*algorithm planning diagram
1.3 粒子群算法
粒子群算法(particle swarm optimization,PSO)[7]最早是由Eberhart和Kennedy于1995年提出,它的基本概念源于对鸟群觅食行为的研究.在PSO中,每个优化问题的潜在解都可以想象成N维搜索空间上的一个点,称之为“粒子”(particle)[8],所有的粒子都有一个被目标函数决定的适应值(fitness value),每个粒子还有一个速度决定它们飞翔的方向和距离,然后粒子们就追随当前的最优粒子在解空间中搜索[8].
粒子群算法的速度和位置更新公式为:
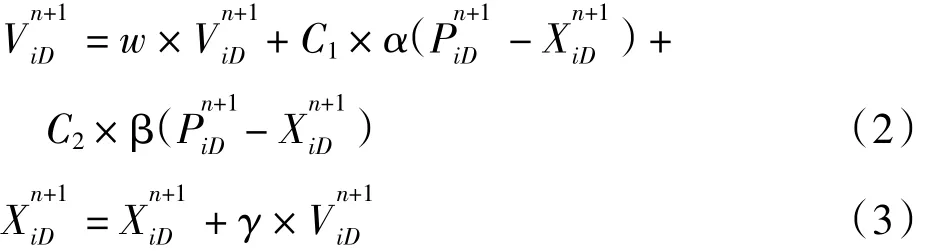
式中:w为保持原来速度的系数,又称为惯性权重;n为迭代次数;D为粒子维度;C1是单个粒子历史最优值的权重系数;C2是所有粒子群体最优值的权重系数;α、β为区间[0,1]之间的随机数;γ为速度系数,设为1.
1.4 分级粒子群-遗传算法
本文对普通粒子群-遗传算法进行了改进,在其基础上对粒子群进行了等级划分,分为:精英粒子、优等粒子群、中等粒子群和劣等粒子群4个类别.其中精英粒子为单个粒子,是适应度值最优的粒子,本文中适应度值为距离总和,因此将适应度值最小的粒子设定为精英粒子;优等粒子群由多个粒子组成,是除精英粒子外,适应度值较小的前几个粒子;劣等粒子群由多个粒子构成,是适应度值较大的最后几个粒子;其余适应度值处于中间位置的粒子全部设为中等粒子.精英粒子作为下次迭代中的父代粒子,不参与交叉和变异;优等粒子群在下次迭代中不参与交叉操作,仅参与变异操作;中等粒子群在下次迭代中既参与交叉操作,又参与变异操作;劣等粒子群采取淘汰操作,即舍弃当前的劣等粒子群,并重新初始化一批粒子加入到总粒子群中,新初始化加入的粒子数目与被淘汰的粒子数目相同.
本文实验中,粒子总数目为50,在对粒子群分级时,精英粒子个数设为1,优等粒子群中粒子个数设为5,劣等粒子群中粒子数设为10,中等粒子群中粒子数设为34.
2 分级粒子群-遗传算法结合A*算法进行路径规划
在大多数情况下粒子群算法相比遗传算法拥有更快的规划速度,但由于粒子的速度和位置更新信息依赖于当前搜索到的最优解,这就导致粒子群算法在规划时容易陷入局部最优[10].而遗传算法具有交叉算子和变异算子[11],能够产生具有新的解集的种群[12],因而在搜索最优解过程中不易陷入局部最优,使得算法能够更好的收敛于最优解.因此,结合两种算法的优点,在粒子群算法中引入遗传算法的交叉和变异操作,以此来扩大粒子的多样性,增强粒子的全局随机搜索能力.
目前,遗传算法中交叉方法有:单点交叉、局部邻域交叉、多点交叉、均匀交叉等[13],本文中采用随机多点交叉的方法,即交叉点的位置随机、数量随机,在对粒子进行变异操作时也采用随机多点变异的方法.这种交叉和变异操作增加了粒子的多样性,实验仿真证明,在处理复杂情况下的问题时,算法在全局搜索最优解能力和稳定性方面有显著提升.
分级粒子群-遗传-A*算法进行机器人多任务目标路径规划主要包括3部分:①构建地图模型;②寻找最优行走路线;③进行避障行走.其具体执行步骤如下:
(1)使用栅格法构建地图模型,如图2所示.栅格标号方式如图2(a)所示,构建障碍物地图时,将障碍物所对应的标号保存在障碍物信息函数map_obstacle中.考虑到机器人的安全和方便路径规划,对障碍物进行扩大处理,如图2(b)所示,其中红色区域为实际障碍物大小,蓝色区域为扩大后的障碍物区域,障碍物扩大值为机器人的半径R.
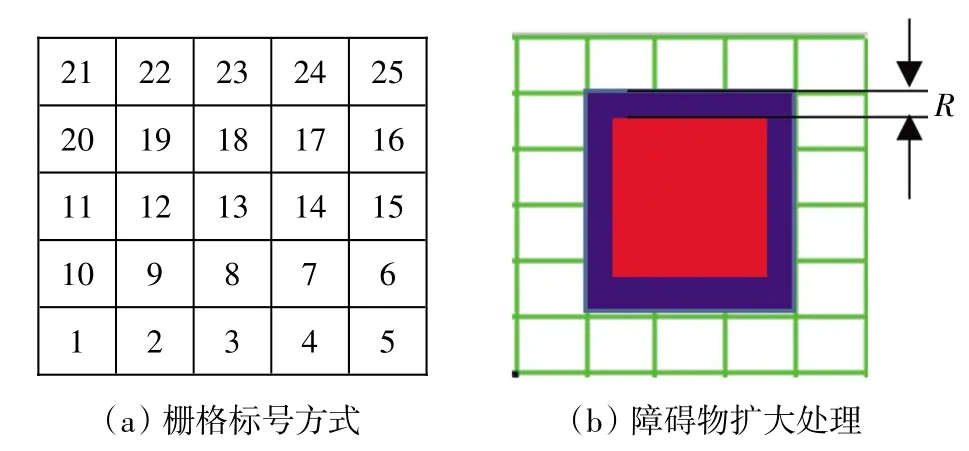
图2 栅格法构建地图Fig.2 Build the map using grid method
(2)将目标点信息导入地图中(起始点也作为目标点),计算任意2个目标点之间的曼哈顿距离,并将所得距离保存在矩阵target_d中,target_d为n行n列方阵,n为目标数.

式中:X_targeti为目标点i的横坐标;Y_targeti为目标点i的纵坐标;X_targetj为目标点j的横坐标;Y_targetj为目标点j的纵坐标.
(3)计算种群适应度值并记录当前全体最优和个体最优,适应度值函数fitness_d表示在不存在障碍物情况下机器人遍历所有目标点后的经过的曼哈顿距离总和,单个粒子的适应度值fitness_dm计算如公式(5):
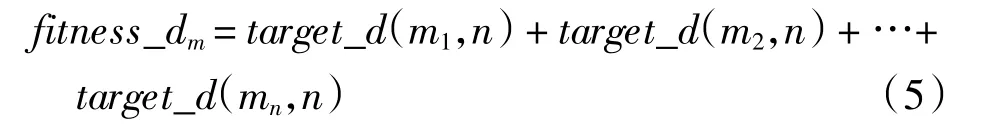
式中:m1,m2,…,mn为 1 ~ n 之间的正整数,且 m1≠m2≠…≠mn.
(4)对个体最优进行交叉和变异操作,记录求得的新适应度值,并将求得的值与历史最优值进行比较,若当前最优小于历史最优,则替换历史最优,并删除交叉和变异操作中产生的相同元素;若当前最优大于历史最优,则保持历史最优不变.
(5)返回步骤(3)重新执行,若求出最优解或者迭代次数达到最大值,终止求解最优行走路线程序,并保存最优行走顺序.
(6)由于步骤(5)中求得的最优行走顺序是将起始点与目标点混合排序的,因此需要将起始点提取到行走路线第一位,且保持行走顺序不变.
(7)调用A*算法,并将map_obstacle中的障碍物信息导入到A*算法的CLOSE列表中,然后以Start点为机器人起始点,Target为各个目标点,按照步骤(6)中行走顺序进行避障行走.进行避障行走时,H(n)的值设为起始节点到当前节点的距离,G(n)的值设为当前节点到目标节点的距离,即:
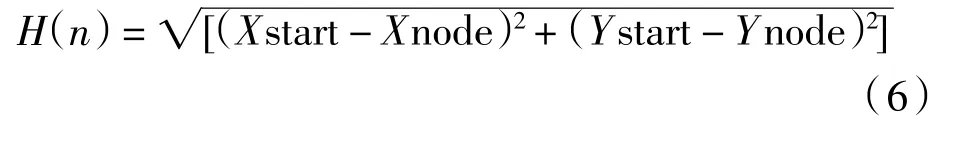
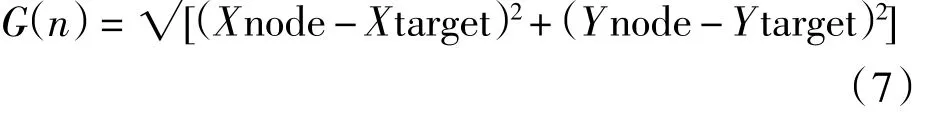
式中:Xstart表示起始节点横坐标;Ystart表示起始节点纵坐标;Xnode表示当前节点横坐标;Ynode表示当前坐标纵坐标;Xtarget表示目标节点横坐标;Ytarget表示目标节点纵坐标.
(8)为机器人规划出行走路程最短、安全无碰的行走路径,程序终止运行.
分级粒子群-遗传-A*算法的路径规划流程图如图3所示.
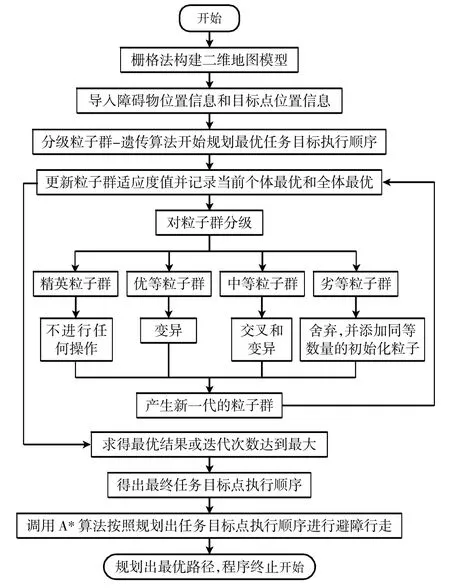
图3 分级粒子群-遗传-A*算法路径规划流程Fig.3 Classification of PSO-GA-A*-algorithm path planning procedure
表1所示为粒子个数都为50,C1=C2=1时,各算法在不同目标数下的求解情况.任务目标点数不同时算法规划对比如图 4 所示.图 4(a)和(b)、(c)和(d)、(e)和(f)分别为任务目标数为5、15和30时的目标点位置分布及规划效果,图 4 中(a)、(c)、(e)为粒子群-遗传算法规划,图 4 中(b)、(d)、(f)为粒子群算法规划.
由图4和表1可以看出,当目标数量较少时,标准粒子群算法和粒子群-遗传算法得出相同的最优解,且标准粒子群算法在规划时间上要优于粒子群-遗传算法;当目标数量较多,目标点位置情况较复杂时,标准粒子群算法进行规划时,在迭代次数和时间上都远远高于粒子群—遗传算法,且规划出的行走顺序不能保证为最优.目标数较少时,粒子群-遗传算法与分级粒子群-遗传算法规划效果差距不大,当目标数量为15时,在迭代次数上,分级粒子群-遗传算法比粒子群-遗传算法降低了25%,在规划时间上,降低了7.5%;当目标数量为30时,在迭代次数上,分级粒子群-遗传算法比粒子群-遗传算法降低了约26.2%,在规划时间上,降低了约11.1%.并且分级粒子群-遗传算法得出的最终结果要优于粒子群-遗传算法的结果.

表1 3种算法规划对比Tab.1 Comparison of three algorithms
分级粒子群-遗传算法和粒子群-遗传算法规划时最小适应度值变化如图5所示.
图5(a)和(b)分别为分级粒子群-遗传算法和粒子群-遗传算法在图4(d)和(f)中目标分布情况下规划时的最小适应度值变化曲线.红色曲线为分级粒子群-遗传算法规划所得,蓝色曲线为普通粒子群-遗传算法规划所得.可以看出,分级粒子群-遗传算法不论是在迭代次数还是规划结果上都优于普通粒子群-遗传算法.
简单和复杂静态障碍物下的路径规划如图6所示.
图6(a)为简单静态障碍物下的遍历多目标机器人路径规划图,图6(b)为复杂静态障碍物下的遍历多目标机器人路径规划图,图中障碍物以蓝色实心栅格表示,各目标点与起始点之间的红色连线为任务目标点的执行顺序,蓝色连线为规划出的机器人行走路径.任务目标点个数为11,以标有Target的绿色方块表示;左下角标有Start的绿色方为起始点,坐标为(3.5,1.5).图 6(c)为在复杂静态障碍物下规划时适应度值随迭代次数的变化曲线,可以看出,当迭代次数约为27时,适应度值达到最小,为69.45,且当迭代次数增加时,适应度值保持不变,表明算法寻找到了最优解.
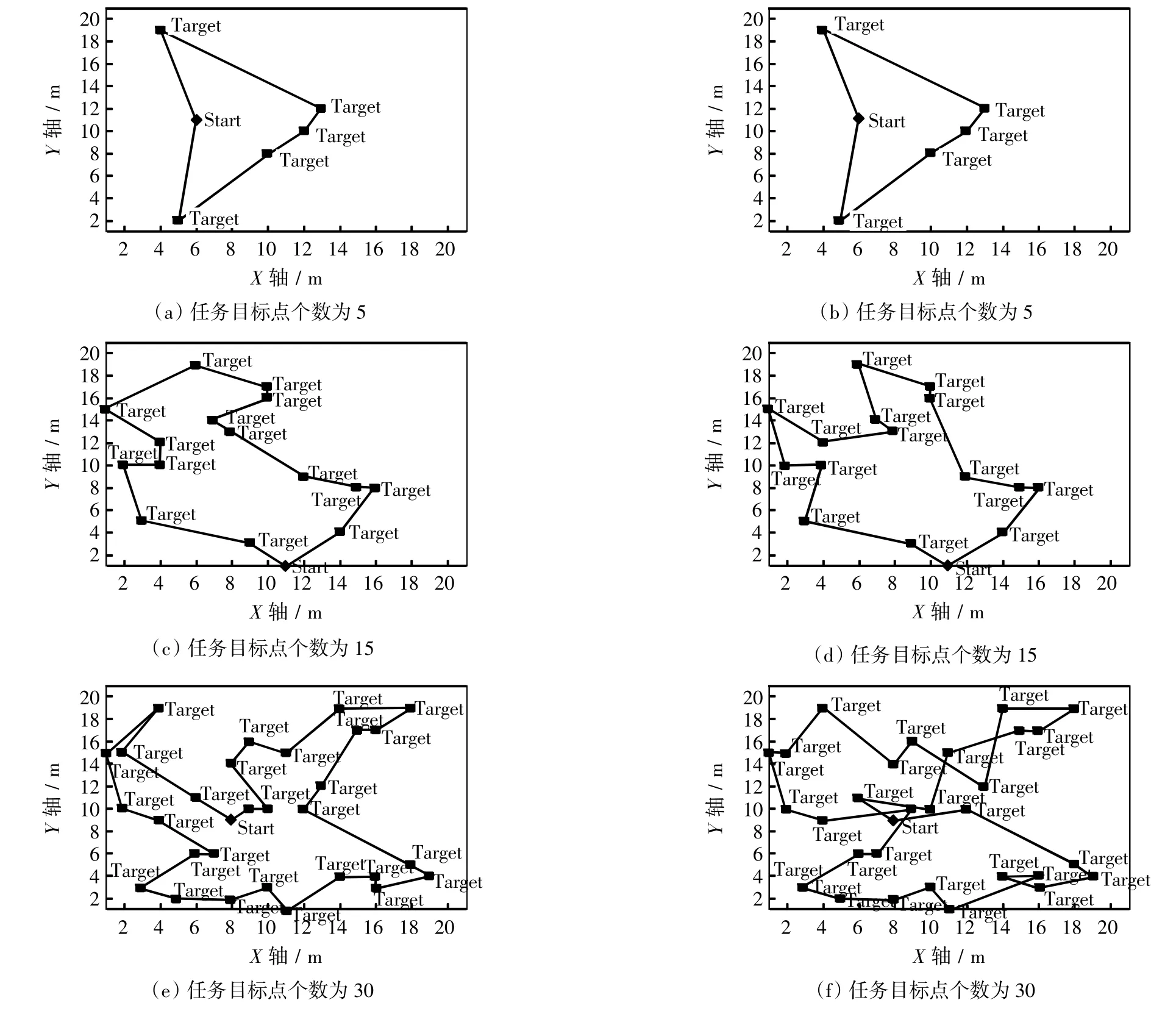
图4 任务目标点数不同时算法规划对比Fig.4 Comparison of algorithm planning in different task target points

图5 分级粒子群-遗传算法和粒子群-遗传算法规划时最小适应度值变化Fig.5 Minimum fitness value that calculated by hierarchical particle swarm genetic algorithm and particle swarm genetic algorithm
图6(b)起始点与目标坐标位置矩阵为ST,矩阵第一行为各目标点的序号,第二行为目标点横坐标,第三行为目标点纵坐标.
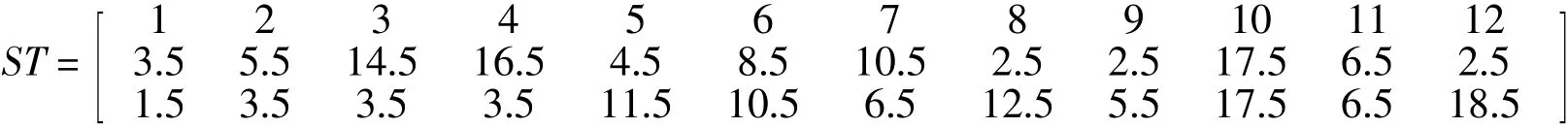
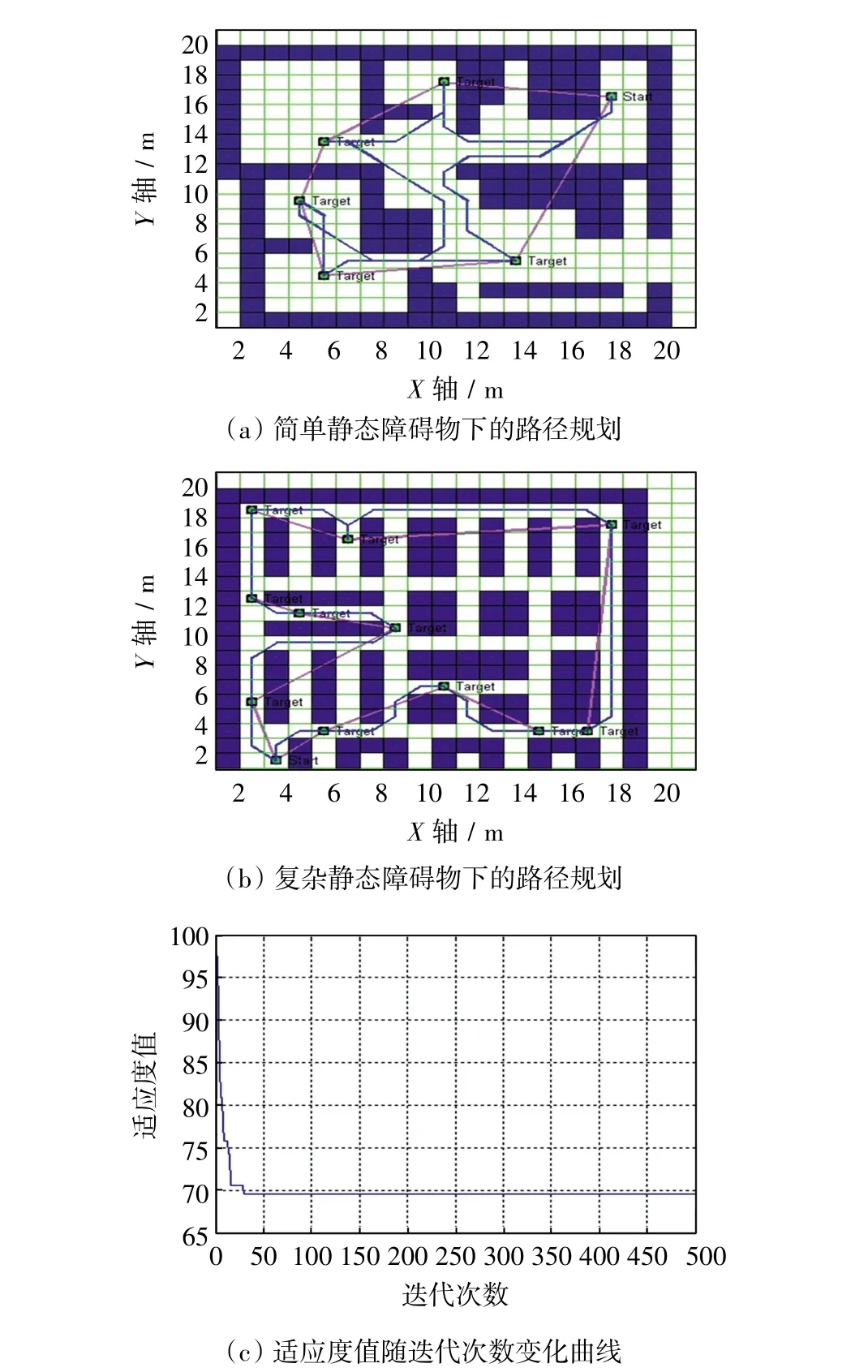
图6 简单和复杂静态障碍物下的路径规划Fig.6 Path planning under simple and complicated static obstacles
经过算法计算后的最佳行走顺序为:1—9—6—5—8—12—11—10—4—3—7—2—1.
由图 6(a)和图 6(b)可知,分级粒子群-遗传-A*算法在障碍物为静态的情况下进行遍历多目标点的机器人路径规划是可行的,并且不论地图障碍物简单或者复杂,任务目标点数量少或者多,算法都能够为机器人规划出一条安全无碰、行走路程短的最优路径.
使用分级粒子群-遗传算法寻找出最优的任务目标点行走顺序,再使用A*算法为机器人规划出一条安全无碰的避障行走路径,最优的目标点行走顺序使得机器人在行走完所有任务目标点后产生最小的移动耗费,而A*寻路算法又为机器人规划出目标点间的最短、无碰行走路径,将这2个最优解结合起来,便组成了机器人多任务目标点的行走最优解,即规划出最优的行走路径.
3 结论
本文提出了一种基于分级粒子群-遗传-A*算法的机器人路径规划新方法,该方法将遗传算法中的交叉和变异操作应用于粒子群算法中,以此来扩大粒子群的多样性,该算法虽然在运行时间上长于粒子群算法,但在处理复杂问题时不易陷入局部最优,且在稳定性方面有了很大提升.仿真实验证明,该算法不论在障碍物简单或者复杂、目标点数量少或者数量多的情况下都能够为机器人规划出最优的行走路径.并且在同等目标点情况下,分级粒子群-遗传算法相比于粒子群-遗传算法,在迭代次数上降低约25%,规划时间上降低约10%.因此,分级粒子群-遗传-A*算法能够成功应用于移动机器人在静态障碍物存在的地图上遍历多个任务目标点的路径规划,并且算法大幅度降低了计算成本,在多任务目标点的路径规划上有着很好的应用前景.
