老龄化背景下储蓄率与经济增长关系研究——基于古典增长模型的分析

贾 非，王士香

(吉林财经大学 统计学院，吉林 长春 130117)

一、引 言

人口老龄化过程将对人类社会产生深刻而持久的影响。我国因老龄化过程中的老龄人口数量多、老龄化速度快、未富先老、城乡失衡等特征，成为世界上应对人口老龄化任务最重的国家之一。人口老龄化是否将对经济增长产生严重的影响以及政府如何做出相应的政策选择，已经成为我国老龄化背景下稳定经济增长以及促进社会发展的重要课题。

关于老龄化过程与经济增长关系的分析，大多集中于考察人口年龄结构变化和养老支出变化对储蓄率的影响，并进而考察其对经济增长的影响。从人口年龄结构角度看，大量文献聚焦于不断上升的抚养比对储蓄率的影响，认为人口总体负担加重将导致经济逐渐丧失第一次人口红利的增长机遇。[1，2]生命周期理论也认为，老龄人口增加将降低社会储蓄率，并对经济增长不利。与之相反，较为乐观的观点是，抚养比不断上升的情况下，人们增加预防性储蓄导致的储蓄率提高，将带来老龄化背景下的二次人口红利。[3]还有观点认为，老龄化对消费与储蓄的影响在不同时间与空间上表现出异质性，这意味着二者关系并非为简单的正向或负向影响关系。[4-6]

从养老支出变化对储蓄率的影响角度看，相关文献将其较为系统地归纳为两种对储蓄率截然相反的影响机制，即养老保险与储蓄相互替代的“资产替代效应”和养老保险对提前退休的吸引力导致退休前增加预防储蓄的“引致退休效应”。[7，8]在实证分析中，相关文献也未取得一致结论。一些文献认为，养老支出对储蓄率的影响取决于养老保险的制度，还有文献得出养老保险对储蓄率影响并不显著的结论。[9-11]综上，关于老龄化背景下储蓄率变化的研究很难取得具有一致性规律的结论，但老龄化过程中储蓄率的变化将对经济增长起到重要影响已成为不争的事实。与以往研究不同，本文的目的是将储蓄率看作老龄化过程的外生影响变量，考察储蓄率对老龄化背景下经济增长的影响。选择这一研究视角的原因如下：其一，老龄化并非仅通过影响储蓄率的路径对经济产生影响，其对经济增长的影响具有多种机制。譬如，老龄化将导致生产要素收益发生显著变化，并对生产能力产生潜在影响[12，13]；人口老龄化催生了消费性服务业的迅速发展，对产业结构优化升级具有明显影响[14]；老龄化过程中增加的养老支出还可能通过挤占政府购买性支出，抑制经济增长。其二，储蓄率是经济、金融、贸易关系中的重要变量，其变化受到多种因素的影响。根据以往文献，除了人口结构和社会保障外，储蓄率还在很大程度上受到实际利率、外部贸易、收入增长、信用发展、房产价格等因素的影响。[15]而我国储蓄率居高不下的主要影响因素是家庭收入和房产价格。[16]这表明，储蓄率的波动绝大部分是外生于老龄化过程的。因此，本文试图简化储蓄率在老龄化进程中发生的复杂变化，将储蓄率看作外生于老龄化过程的经济变量，并考察老龄化过程中，老龄化程度、养老支出对经济增长的影响如何取决于储蓄率的变化。从这一角度看，本文的分析丰富了老龄化背景下储蓄率与经济增长关系的理论，从而扩展了老龄化相关研究的理论边界。

二、理论模型与假设

新古典经济增长模型几乎是所有增长问题研究的出发点。该模型主要包含产出 (Y)、资本 (K)、劳动 (L) 和技术进步 (A) 四个变量，技术进步进入模型的方式主要有三种类型：哈罗德中性、索洛中性和希克斯中性。本文主要考虑哈罗德中性即劳动加强型的经济增长模型，此时生产函数的形式为：

Y=F(K,AL)

假定规模报酬不变，定义k=K/AL，y=Y/AL，分别表示每单位有效劳动的平均资本和每单位有效劳动的平均产出，则生产函数可写成如下集约形式：y=F(k,1)，定义f(k)=F(k,1)，则y=f(k)，该式满足f(0)=0，f′(k)>0，f″(k)<0以及稻田条件。

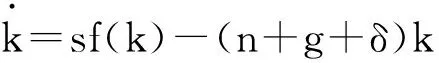
(1)

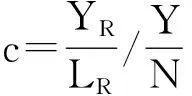
(2)

图1 老龄化背景下经济平衡增长路径

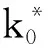
假设1：老龄化程度 (a) 加深对平衡增长路径下人均产出 (y) 的影响取决于储蓄率 (s) 的高低，较高的储蓄率将强化人口老龄化对人均产出的负向影响。

假设2：养老水平增加 (c变大) 对平衡增长路径下的人均产出 (y) 具有负向影响。

假设3：储蓄率(s)越高，养老水平对人均产出(y)的负向影响越强；反之，储蓄率(s)越低，养老水平对人均产出(y)的负向影响越弱。

三、样本、变量与研究方法

(一) 样本与变量

本文选择我国31个省 (市、自治区) 作为样本进行研究，样本区间为2005～2016年，所有数据的来源为wind资讯金融终端宏观数据库。本文的实证分析包含如下变量：

被解释变量：实体经济增长 (y) ，用人均产出表示，由各省生产总值 (GDP) 与总人口之比计算得出，单位为万元/人。

解释变量：老龄化程度(a)，用老年人口比表示，由各省市历年60岁以上人口抽样数与全部人口抽样数做商得到。[注]由于缺失2010年各省市的人口抽样调查数据，因此2010年老年人口比数据无法得到，本文使用平均数公式，运用插值法进行补齐。养老水平(c)，用老年人人均养老保险额度(养老保险支出与60岁以上人口数之比)除以人均收入(生产总值与总人口之比) 得出，该变量表示相对全社会人均收入，老年人口的人均收入水平。储蓄率 (s)，在假设储蓄全部转化为投资的前提下，储蓄率近似与资本形成率相等，因此，文中储蓄率由各省市历年资本形成总额占总产值的比例表示。

控制变量：少儿抚养比 (ccr)，由各省市历年0～14岁人口抽样数与全部人口抽样数做商得到；财政支出 (fex)，由各省地方人均公共财政支出表示，单位为万元/人；净出口 (nex)，由各省出口总额与进口总额的差与该省总人口做商得到，单位为万元/人。

表1中给出上述变量的描述性统计分析与相关系数矩阵。可以看出各个解释变量之间相关系数均处于0.5以下，说明变量之间没有明显的多重共线性问题。尽管如此，我们依然计算了方差膨胀因子，结果显示VIF值处于2.46以下，远低于临界值10，进一步证明了变量之间不存在明显的多重共线性问题。

表1 变量描述性统计与相关系数矩阵

为了保证模型的稳定性，在实证分析之前对各变量进行平稳性检验。为确保检验结果的稳健性，选择IPS方法和LLC进行检验。尽管相对于允许个体单位根过程和异构参数的IPS检验而言，LLC检验假设参数具有同质性可能导致检验结果存在异质性偏差，但LLC检验仍然可以作为补充，验证IPS检验结果的稳健性。检验结果见表2。可以看出，ccr变量的IPS检验结果是非平稳的，但LLC检验的结果是在95%的置信度下平稳的，所有其它变量IPS检验都是平稳的。因此，可以认为所有变量均通过平稳性检验。

表2 变量单位根检验

注： *、**、***分别表示该统计量在10%、5%和1%显著水平上显著。

(二) 研究方法

宏观经济变量之间通常存在理论上的相互因果关系，在本文构建的模型中，经济增长变量可能通过影响人口寿命而影响老龄化程度，同时也能够对养老水平和储蓄率产生影响，因此，解释变量具有理论上的内生性问题。为此，本文使用面板平滑转移模型 (PSTR模型) 进行参数估计，因为该模型能够有效限制因解释变量内生性导致的估计偏差。[17]尽管如此，为控制内生解释变量问题，本文仍在模型中将全部的解释变量和控制变量滞后一期，因为经济增长很难对上一期的老龄化程度、养老水平和储蓄率产生影响。

本文的实证分析中采用的PSTR模型是一个包含外生变量的固定效应面板回归模型，其系数可随时间和个体的变化而发生变化。[18]PSTR模型是平滑转移回归 (STR) 模型的拓展，是为个体和时间上存在异质性的面板数据进行建模使用的。该模型假设参数是一个可观测变量的有界连续函数，并允许回归系数之间存在异质性。包含两个区制和一个转移函数的简单PSTR模型可以被定义为：

(3)

式(3)中xit对yit的影响可以表示为：

(4)

其中，转换函数g(qit;γ,c)是可观测变量qit的连续函数，转换函数经过标准化后介于0和1之间。我们考虑如下逻辑转换方程：

(5)

其中，c=(c1,…,cm)′是一个m维的位置参数向量，式中参数满足γ>0且c1≤ c2≤ …≤cm。

包含多个转移函数的PSTR模型可表示为：

(6)

若对于所有的j=1,…,r，都有γj→∞，转移函数转变为一个示性函数I(A)，式(6)就变成一个包含r + 1个区制的PTR模型。因此，多层次PSTR模型可视为多区制PTR模型的一般化过程。

模型估计过程如下：首先，进行模型的线性和剩余非线性检验，如果拒绝了模型不存在非线性的原假设，则表明样本数据可以使用PSTR模型进行建模，否则应使用传统面板固定效应模型建模。其次，对模型转换方程的个数进行检验，这一步骤将对不断增加转换函数个数进行假设检验，直至模型不再含有剩余的非线性部分，即确定转换函数的个数。最后，对模型的参数进行估计，运用非线性最小二乘法 (NLS) 进行面板参数估计，确定转换参数、位置参数、固定效应影响系数和转换函数影响系数。

四、实证结果

(一) 非线性检验与转换方程的个数确定

非线性检验的原假设与备择假设是H0: r = 0，H1: r = 1，假设检验的统计量为LM统计量和LMF统计量。根据表3的结果可知，无论在m = 1还是m = 2的情况下，模型均能够在5%的显著水平下拒绝r = 0的原假设，这意味着解释变量与被解释变量之间存在非线性关系。剩余非线性检验的原假设与备择假设分别是H0: r = 1，H1: r = 2，根据表3中统计量LM和LMF的计算结果可知，无论在m = 1还是m = 2的情况下，模型均接受了r = 1的原假设，说明模型均存在一个转移函数。进一步，根据AIC和BIC值的比较可知，模型在m = 1时表现最佳。为此可以得出结论：模型均为具有1个转换函数1个位置变量的PSTR模型。

表3 线性和剩余非线性检验结果

(二) PSTR模型估计结果

表4中给出了模型的参数估计结果。模型1的门限变量为储蓄率，其位置参数值为0.501，说明当储蓄率处于0.501两侧时，各变量对人均产出的影响明显不同，但这种变化是平滑转换的，其平滑参数值为8.386，意味着平滑转换的速度较快。根据回归参数可知，在位置参数两侧，老龄化水平和养老水平对人均产出的影响均在1%的显著水平下显著。当储蓄率为0.501时，老龄化水平 (a) 对人均产出 (y) 的影响系数为-0.305；当储蓄率小于0.501时，这一影响系数大于-0.305，随着储蓄率逐渐变小，其影响系数最终稳定于-0.063；当储蓄率大于0.501时，该影响系数小于-0.305，随着储蓄率逐渐变大，其影响系数最终稳定于-0.548。这一结果表明，随着储蓄率增大，老龄化水平 (a) 对人均产出 (y) 的负向影响增强，该结果支持假设1。同理，当储蓄率为0.501时，养老水平 (c) 对人均产出 (y) 的影响系数为-4.324；当储蓄率小于0.501时，这一影响系数变大，并随着储蓄率逐渐变小，其影响系数最终稳定于-1.208；当储蓄率大于0.501时，该影响系数变小，随着储蓄率逐渐变大，其影响系数最终稳定于-7.440。该结果意味着，储蓄率增大过程中，老龄化水平 (a) 对人均产出 (y) 的负向影响增强，该结果支持假设3。养老水平对人均产出的影响始终为负数，这表明养老水平增加始终对人均产出具有负向影响，这一结论支持假设2。因此，PSTR模型的估计结果支持了所有的理论假设。

表4 PSTR模型参数估计结果

注：*、**、***分别表示在10%、5%和1%显著水平上显著。

五、结论与启示

关于老龄化、养老支出与经济增长关系的研究，以往文献通常聚焦于储蓄率的中介作用，即老龄化、养老支出如何影响储蓄率并进而对经济增长产生影响。与以往研究不同，本文假设储蓄率外生于老龄化过程，并以这一假设为前提，在新古典经济增长模型中加入了老龄化的经济要素，推导了老龄化背景下的经济增长模型。根据模型给出的理论启示，本文运用限制了解释变量内生影响的PSTR模型，验证了储蓄率的变化在老龄化和养老支出对经济增长产生影响过程中的作用。实证分析结果显示，老龄化和养老支出对经济增长的影响程度取决于储蓄率的高低。具体而言，储蓄率越高，老龄化和养老支出对经济增长的负向影响越大，这意味着，对于储蓄率较高的地区，宏观政策应格外关注老龄化带来的经济负效应。本文的理论与实证分析，揭示了储蓄率在老龄化背景下对经济增长影响的新机制，从而丰富了以往关于储蓄率与经济增长关系的理论。