基于距离度量学习的棉花品级分类方法研究

张婷 ，高颖 ，王东 ，吕炎 ，董军宇 ，亓琳 *，陈鹏

（1.华中师范大学/国家数字化学习工程技术研究中心，武汉430079；2.中国海洋大学信息科学与工程学院，山东青岛266100；3.山东出入境检验检疫局，山东青岛266001）

棉花是我国的主要农作物和大宗进口商品，也是检验检疫实施批检验的特殊进口商品。近年来，国内棉纺织行业的迅速发展带动棉花的需求量不断增加，国内棉花市场缺口日益增大。但由于国内棉花的播种面积不断下降，导致每年国内均需要进口大量棉花。2010年棉花进口量为267万t，2011年为330万t，2012年则达到了513万t[1]。棉花自实施检验以来，其外观品级一直是反映棉花品质好坏的重要因素之一，也是棉花价格的决定因素之一，在棉花的进出口贸易中扮演着重要的角色。品级多年来一直沿用人工评级的方法，对照实物标准或成交小样，确定进口棉花的品级等级及降级幅度。品级人工检验存在一定的不足之处，如需要人力较多，检验效率低，受光线等检验条件的影响较大，检验时间长时易产生人为误差等。而进口棉花品种多样，变化反复的情况则使得这种弊端更为放大。如何消除这些不利因素，一直是棉花检测行业研究的重点。

图像处理技术的日益成熟和机器学习技术、距离度量学习技术的快速发展，为从图像角度出发研究棉花品级分类的算法奠定了基础。采集棉花的图像，进而从图像中提取相应的特征来表征棉花外观，最后使用距离度量学习、机器学习技术来训练出1个鲁棒性高的分类器，以达到对棉花品级自动分类的目的。

本文从3个方面来介绍基于距离度量学习的棉花品级分类算法：数据采集和图像预处理、特征提取、分类器设计。色泽、杂质和轧工是训练有素的工人在判断棉花的品级时考虑的3大因素。本文根据这3个因素，从棉花的数字图像中提取相应的计算特征来表征棉花的属性。本文使用主成分分析法对数据集进行预处理，降低特征向量的维度。然后使用大边界最近邻算法 （Large margin nearest neighbor，缩写为LMNN）通过半定规划（Semidefinite programming）[2]学习得到1个马氏距离度量矩阵。最后训练1个k近邻（k-nearest neighbor，kNN）分类器，从而实现棉花品级的自动分类。

1 数据采集与图像处理

1.1 数据采集

美国陆地棉的级别共分为5大类[3]，分别为白棉（White）、淡点污棉（Light spotted）、点污棉（Spotted）、淡黄染棉（Tinged）、黄染棉（Yellow stained）。本文着眼于陆地棉中的白棉，共分为7个等级（质量依次递减）， 分别为：Good middling、Strict middling、Middling、Strict low middling、Low middling、Strict good ordinary、Good ordinary[3]。

本文使用Canon EOS 20D数码单反相机，以美国棉花中的作为采集对象，在山东检验检疫局国家进口棉花检测实验室进行图像数据的采集。采集的数据范围为：白棉的7个级别对应的标准盒，以及进出口贸易常见的前4个级别对应的非标准盒样本。为保证每次采集的硬件环境一致，每次采集都位于实验室的同一位置，并使相机视线与棉花放置的平面成垂直关系，从而减少阴影，如图1所示。

图1 数据采集装置简易图

光源为实验室设置的D65光源，是标准光源中最常用到的人工日光，色温为6500K。由于对棉花外观品级的判断很大程度上依赖于其色泽特征，因此拍摄图像质量的好坏严重影响后期的判断。拍摄图像的格式为RAW。RAW格式的图像是传感器记录的原始信息，以尽可能保证数据的准确性。

1.2 图像预处理

本文采用MATLAB 2010进行数据处理。与其他格式相比，RAW格式的优点在于它能够被转化为16位的图像，在保证数据原始性的前提下，精度远远高于8位的图像。本文将RAW格式的图像线性转化为16位的TIFF（Tagged image file format）文件。经过转化后的图像如图2所示。

1.3 特征提取

由于进口棉花的品级等级由色泽、杂质和轧工3个因素决定，本文针对这3个因素拟提取相应的计算特征对其进行数学描述。

1.3.1色泽。所谓色泽，指的是颜色和光泽度。针对这一因素，将在CIELAB颜色空间里提取特征来对其表征。HVI通过测量棉花的反射率和黄度来反映其色泽级别。 反射率（Reflectance degree，Rd）指的是棉花的明暗程度，用百分比表示，数值大表示反射率高，棉花明亮；黄度（+b）指示棉花黄色色调的深浅，数值越大代表棉花越黄[4]。Rd和+b都来源于20世纪三四十年代Nickerson和Hunter的研究[5]。如图3所示，在Hunter系统颜色空间中，颜色由三维的空间点（Rd，a，b）描述。

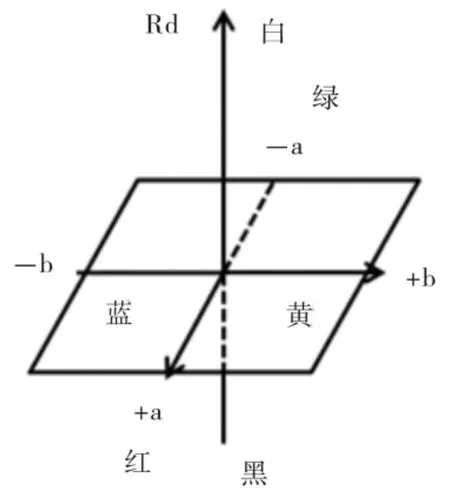
图3 Hunter系统颜色空间示意图

反射率和黄度在棉花色泽的测量中扮演着十分重要的角色，但随着人们对全球棉花贸易的关注，人们希望采用更被普遍接受的测量标准来测量棉花的色泽。CIE L*a*b*是国际公认、十分成熟的颜色模型，由国际照明委员会 （International Commission on Illumination，CIE）在 1976 年提出，是对Hunter Lab颜色空间的改进[6]。目前，CIE L*a*b*在许多行业中得到广泛使用。表1对这2个颜色模型从各个方面进行了比较，其中在敏感度方面，CIE L*a*b*颜色空间对于黄色更为敏感。

此前，很多人尝试采用L*a*b*系统测量棉花的色泽。1988年Aspland等试图将Rd、+b参数变换为CIELAB的坐标，即将美国农业部制定的比色图由（Rd，+b）形式改为（L*，b*）形式[7-8]。 2008 年，Thibodeaux等对HVI颜色标准和CIELAB坐标系的相关性进行了研究，结果表明标准CIE颜色参数（L*，b*）与 HVI的颜色参数（Rd，+b）具有非常好的相关性[9]。本文在已有的研究基础之上，从棉花图像的角度出发，开展了下述工作。

假设棉花图像的像素为M×N。首先提取CIELAB空间每个颜色通道的均值，作为棉花样本的1个特征。公式如下：

表1 Hunter Lab与CIE L*a*b*的比较

其中L*ij代表图像中每个像素点的L*通道的值。其他2个颜色通道与此类似。HVI只是对棉花样本的每个颜色通道的均值进行了测定。而实际上，颜色的均匀性对于棉花等级的判定也是1个很重要的因素。因此，本文提取了不同尺度上的方差作为表示颜色均匀性的特征。首先计算整幅图像每个颜色通道的方差，即选择的基本单位为单个像素，分别表示为，它们是对整体颜色均匀性的测定。然后以n×n（n小于M、N）像素的方块作为基本单位，这个基本单位的颜色值用块内所有像素点的均值来表示。假设一共划分出互不重叠的Q个小块。

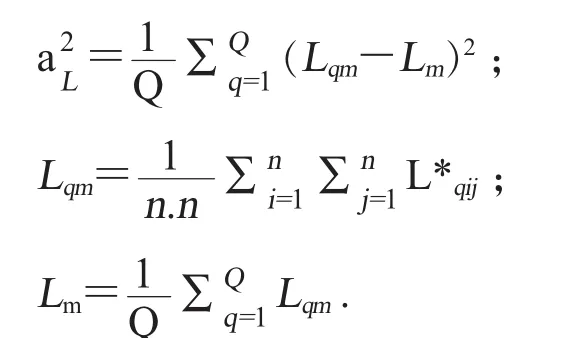
1.3.2杂质。杂质，是指混入皮棉中的一些非棉纤维物质和不孕籽、棉籽、破籽、籽屑和籽棉等。为了能够准确地提取特征来描述杂质这一因素，首先要做的就是有效地识别杂质。因杂质和棉花的亮度差别较大，一黑与一白，所以要对图像的L*通道处理，识别杂质。杂质识别后，可以得到一个二值图像，提取该二值图像上的杂质总面积、块数、平均大小、分布4个特征作为对杂质这一因素的表征。

1.3.3轧工。轧工的好坏表示的是籽棉经过轧花工序后皮棉的光洁、柔顺、粗糙、杂乱的程度。在美国农业部的566号农业手册[13]中，有关于“Preparation”和“Extraneousmatter”的定义。 “Preparation”用来描述皮棉的光滑和粗糙程度。“Extraneousmatter”用来描述棉花中除纤维和叶屑外，所含的另外的物质，例如草根、树皮、籽屑、灰尘、油污等。

综上，轧工包括2个方面的内容：一是它的外观形态，表面平滑或粗糙，棉花表面的纠结程度；二是所含疵点的程度。关于疵点的检验，在杂质提取时能一定程度上识别出来，所以这些内容在针对“杂质”提取的特征中有所体现。对于外观形态的粗糙度，通过提取纹理特征——灰度共生矩阵（Gray level co-occurrence matrix，GLCM）来表示。 Duckett等在文章中也提到，纹理是人眼观测到的1个很重要的特征[8]。纹理分析的方法在纺织品中的应用也在前人的研究中有所体现[14-16]。人类视觉感知对二阶统计量十分敏感，因此，选择图像的灰度共生矩阵的二次统计量对纹理进行描述。

灰度共生矩阵是1种通过分析图像像素灰度值的空间分布相关性来描述纹理的方法。常用的灰度直方图是对图像中每个灰度级出现频率的统计结果，与空间位置无关；而灰度共生矩阵是对图像中相距某个固定距离的2个像素点分别具有某灰度的情况进行统计得到的[17]。假设存在1幅N×N像素的图像，取其中的任意一个像素点（x，y）以及另外1个与它有固定间隔的像素点（x＋m，y＋n），它们对应的灰度值分别为f1和f2，这一像素点对的灰度值表示为（f1，f2）。 令像素点（x，y）在整幅图像上以 1 个像素点为间隔顺序移动，则会得到不同（f1，f2）值。如果该图像是8位图像，即灰度值的级数为256，那么（f1，f2）有2562种不同的组合。遍历整个图像，统计每一对（f1，f2）出现的次数，以矩阵的形式记录下来。最后将统计得到的次数归一化为频率，形成的矩阵就是灰度共生矩阵。间隔（m，n）可以有不同的取值，具体可以依据纹理的特征来设定。针对细的纹理，选择小的间隔值；反之，选择较大的间隔值。当m=1，n=0时，像素点对是水平分布的，此时对应的是0°方向上的灰度共生矩阵；当m=0，n=1时，像素点对是垂直分布的，此时对应的是90°方向上的灰度共生矩阵；与此类似，当m=1，n=1 时，对应的是 45°方向；当m=－1，n=1时，对应的是135°方向。

由于通过灰度共生矩阵计算出的一些标量，可以用来表示纹理的特征。针对棉花图像，本文选定步长为 1，方向为 0°、45°、90°、135°的 4 个灰度共生矩阵进行计算。针对每个灰度共生矩阵，计算其能量、熵、对比度、相关性4个纹理参数。然后，求能量、熵、对比度、相关性的均值和标准差作为最终8维纹理特征。

综上所述，本文一共提取了21个特征来表征棉花图像，包括 9 个色泽特征[均值（L*）、均值（a*）、均值（b*）、方差（L*）、方差（a*）、方差（b*）、方差（L*）（32×32 像素的方块）、 方差 （a*）（32×32 像素的方块）、方差（b*）（32×32 像素的方块）]，4 个杂质特征（区域百分比、平均大小、数量、杂质的分散程度），8个轧工（GLCM）特征[平均值（能量）、标准差（能量）、平均值（熵）、标准差（熵）、平均值（对比度）、标准差（对比度）、平均值（相关性）、标准差（相关性）]，也就是说，每幅图像对应1个21维的向量。

1.4 分类器设计

基于以上得到的特征数据设计、训练合适的分类器，并测试其性能。棉花定级人员的棉花分类能力也是花费大量的时间、精力来学习获取的。因此，本文将机器学习（Machine learning，ML）的技术应用到棉花品级分类算法的研究中，利用大量的已分类的棉花样本来训练分类器，使得分类器具备棉花定级能力，从而将人的眼睛从这项工作中解放出来。具体的机器学习算法包括人工神经网络、决策树、k近邻分类算法（kNN）、支持向量机等[18]。本文主要研究最近邻分类算法及其后续发展的一系列算法在棉花分类中的应用。图4为棉花分类方法的流程。

图4 棉花分类方法的流程

（1）特征数据降维。采用主成分分析（Principal component analysis，PCA）的方法对前面得到的数据降维，减少数据冗余，以便后续的分析。假设选取100个样本，把数据表示成100×21的矩阵形式。降维之前，需要对数据逐列（每列代表的是100个样本的同一个特征）进行归一化处理，使每列的数据减去本列数据的均值，除以标准差。最后得到的是均值为0，标准差为1的数据，方便以下的计算。

设X＝（x1，…，xp）T是 1 个p维随机向量，均值向量EX＝u，协方差矩阵DX＝V≥0。来自某个总体X的样本有p个特征变量，主要的任务是要将这p个特征变量x1，…，xp组合成少数几个综合性变量y1，y2，….，yq（q＜p），同时要求新的综合变量能涵盖原来p个特征变量所包含的信息，并且q个综合变量互不相关。针对本文中使用的样本，p应该为21，q是＜21的正数。 将y1取为x1，x2，…，xp的线性组合，即：

其中，a1=（a11，a12，…，a1p）T为非 0 常向量。选取合适的非零向量a1，使得y1能尽可能多地包含原来p个特征变量所具有的信息，也就是说经过变换后得到的y1具有最大的方差

（2）Multiple-metricsLMNN。最初提出的 LMNN分类框架存在1个明显的局限性：针对输入的所有样本数据，都是使用同一个马氏距离度量来计算样本间的距离。将度量记为M＝LTL，那么可以看到马氏距离[19]本质上就是欧式距离[20]的全局线性变换，即x→→Lx→，这样的变换不适用于训练数据中的非线性变化。Weinberger等[21]对singlemetricLMNN进行了改进，提出了Multiple-metricsLMNN的概念。

假设将数据集划分为P个不相交的子集其中当 α≠β 时那么在kNN分类中，每个Pα都有自己的马氏距离度量Mα。输入1个测试特征向量计算它与训练集中任意向量属于子集 αi）的距离的平方，公式如下：

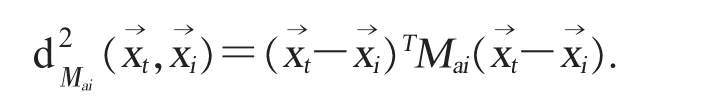
将计算出的距离大小排序，选出的最近邻，从而确定其类别。 在 LMNN 分类中，假设是的1 个目标邻居。 首先，使用Mai计算与间的距离；第二步，使用Mai计算与潜在的冒名目标邻居间的距离；最后，将半正定约束条件改写为多个。综上所述，这些步骤又形成了新的半正定规划问题。如下所示：

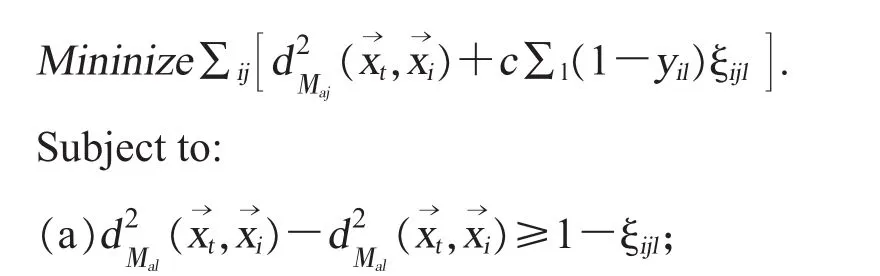
（b） ξijl≥0；

（c）Ma为半正定矩阵。

2 棉花品级分类算法应用试验

2.1 杂质识别试验及结果

为了提高试验的准确性，首先要进行杂质识别。在杂质识别试验中，通过对图像进行归一化处理，并在归一化后的图像基础上寻找边缘以检测灰度变化，从而提高方法的鲁棒性。因此本文利用sobel算子对归一化后的图像进行边缘检测[12]，得到二值图像。如图5（b）所示，每个小杂质块是一个连通域。

对所得图像进行阈值分割，得到另一张二值图像。并对2幅二值图像进行“与”操作，最后通过消除噪声点，将只有1个像素点的杂质去掉。图6为7个级别的杂质识别结果。

图5 杂质识别

对所得图像进行阈值分割，得到另一张二值图像。并对2幅二值图像进行“与”操作，最后通过消除噪声点，将只有1个像素点的杂质去掉。图6为7个级别的杂质识别结果。

2.2 棉花品级分类试验及结果

本试验将大边界k近邻算法应用到棉花分类中。根据特征数据的降维方式，先后设置不同的k值和维度值，根据不同维度值对应的贡献率的大小选取适合的维度值，本试验中选取的维度为10维和15维2种，对应的累积贡献率分别为99.80%和99.99%。

2.2.1基于标准盒的棉花品级分类。每个品级选取了108个标准盒样本，组成了大小为756（108×7=756）的样本集。其中70%用来训练，30%用来测试。不同的参数设置对应的分级效果如图7所示。

从图 7 可以看出，当方法（kNN、LMNN（10）、LMNN（15）等）相同时，k=1对应的试验的错误率最小；当k值相同时，方法 LMNN（10）或 LMNN（15）可取得最好的试验效果。综上所述，当参数k=1时，使用LMNN（15）的方法得到最小的错误率1.32%。

图6 杂质识别结果图

图7 不同参数下基于标准盒的棉花分级效果

2.2.2基于标准盒和非标准盒的棉花品级分类。上述试验的数据仅包含标准盒样本，而在实际应用中，针对非标准盒样本的准确率才是最需要关心的问题，因此后续试验中加入了非标准盒样本（仅常见的前4个级别的非标准盒样本）。本试验数据集包括：（1）标准盒样本共 432 个（108×4）；（2）非标准盒样本349个 （因为非标准盒样本的有限性，每个级别的样本个数没有完全统一，但大致相同）。因此，本试验的样本集大小为 781（432＋349），70%用来训练，30%用来测试。结果如图8所示。

图8 不同参数下基于标准盒和非标准盒的棉花分级效果

2.3 结果分析

由上述试验结果可以看出：（1）是否使用PCA降维，对分级结果影响不大。在基于标准盒的棉花品级分类试验中，使用PCA降维的分级准确率比LMNN的结果稍高；基于标准盒和非标准盒的棉花品级分类试验中，使用PCA降维的分级准确率比LMNN的结果稍低。特征向量的维数是21，本身不属于高维数据，因此是否使用PCA法对计算量的影响也不大。

（2）MM LMNN法的分级结果与LMNN法基本持平，仅在图8b所示的结果中有所提高。因此，可以说马氏距离度量法适用于整个棉花样本集。

（3）加入非标准盒样本后的分级准确率下降。下降的原因分析如下：第一，标准盒样本属于人工制作的样本，从整个样本来看，无论是杂质、色泽，还是轧工技术，分布得都很均匀；因此500×500像素的图像（本文中的样本都是500×500像素的）能很好地代表1个品级的特征。而非标准盒样本的杂质、色泽、轧工技术分布不均匀，用500×500像素的图像不能很好地反映1个品级的特征（这一点也是未来要完善的）。第二，标准盒样本十分平整，而非标准盒样本凹凸不平，由于自身的遮挡会产生阴影，这也是造成分级准确率下降的原因之一。第三，对于非标准盒样本的分类准确率计算，本文是通过将分类器给出的结果与工人给出的级别相比较得出，但是并不能保证工人的判断完全正确。

3 结论

本文从图像的角度出发，提出了一种非常经济高效的棉花品级自动分类方法，解决了人工检测棉花中的效率低、主观性强等缺点。本文首先从图像中提取能反映棉花属性的相关特征，之后再用距离度量学习、机器学习算法对这些数据进行学习训练，得到1个高准确率的分类器。

本文所提出的棉花等级分类方法，完全从图像的角度出发，通过计算棉花样品的L*、a*、b*的均值、方差等值，更全面地反映棉花图像的色泽特征。从视觉感知的角度出发，提取棉花的纹理特征，使其能很好地表征轧工。并通过图像处理对棉花的杂质情况进行了有效表征。同时将评价棉花外观好坏的色泽、杂质和轧工这3个指标都考虑进来，提出了1种完备的棉花品级自动分类方法，并将机器学习和距离度量学习的技术应用到棉花品级分类中。应用试验证明本文提出的方法可以有效实现棉花品级分类。