导航卫星伪码与载波测距观测量偏差机理分析

皇甫松涛 刘彬 刘天雄 谢军

(北京空间飞行器总体设计部，北京 100094)

在轨伪码和载波测距观测量是卫星无线电导航系统定位、导航与授时(PNT)服务的基本观测量。卫星导航系统工作的基本原理是用户同时测得多颗导航卫星的伪码和载波测距观测量，得到与卫星之间的距离，进而计算用户三维坐标。正常情况下，二者之差应为零均值的观测噪声，否则就说明导航卫星在轨伪码或载波测距观测量发生了变化，这样会直接影响导航系统的定位精度。

2015年，针对北斗、GPS、Galileo和GLONASS四大导航系统，文献[1]使用全球多个监测站的数据进行在轨伪码测距观测量分析，发现了北斗区域系统卫星下行信号的伪码测距观测量与载波相位观测量之间存在异常偏差的问题，并且偏差值与仰角相关，最大偏差值约为1.5 m，而GPS、Galileo和GLONASS系统均不存在上述异常现象。该文献虽然描述了北斗系统的异常，并在观测量统计结果的基础上给出了修正模型，但并未分析可能导致该问题的原因。

类似的异常现象曾在GPS系统出现。2009年，文献[2]与文献[3]等对GPS和GLONASS系统进行在轨伪码测距观测量分析，发现GPS的SVN49卫星伪码测距观测量与载波相位观测量之间存在米级的偏差，而GLONASS和GPS早期Block IIA卫星型号均未出现该问题。文献[4-5]将上述问题定位为：由于L5射频信号附加端口存在设计问题，天线阵元外圈射频信号反射，在内圈耦合口处叠加形成了多径。

上述文献均用到了多径(Multipath，MP)分析方法，该方法在消除电离层及对流层延迟的前提下，计算伪码测距观测量与载波相位观测量之间的差值。多径对载波相位观测量的影响比对伪码观测量低两个数量级[6]，即多径信号对接收机伪码相位测量的影响远超过载波相位影响。因此MP分析方法可以将接收机载波相位观测量作为距离参考基准，来评估多径引起的伪码测距观测量偏差。

由上可知，有理由怀疑北斗导航卫星在轨伪码测距观测量发生了变化，并且该变化与空间段自身多径有关。而造成卫星信号多径的因素是多方面的，本文建立多径效应评估数学模型，就作用机理开展仿真分析，根据分析结果，识别伪码测距观测量变化的原因，准确定位导航卫星在轨伪码测距观测量的变化机理，从而指导卫星设计与地面试验验证工作。

1 多径效应数学模型

无论是卫星自身多径还是环境多径，其对伪码测距观测量的影响均类似：使用户段接收机的伪随机码相关峰发生畸变，造成环路跟踪偏离，进而导致伪码测距观测量与实际值偏离。假设接收机主径接收信号为

sd(t)=AP(t)ej(ω0t+θ0)

(1)

式中：A为接收信号幅度；P(t)为基带数据，就导航系统而言，一般为伪随机码和电文调制后的双极性不归零信号；ω0为信号角频率；θ0为主径信号到达载波相位；t为时间。

多径信号较主径而言，传输时延为τd、幅度衰减为Ad、相位变化量为θd。那么多径干扰下，接收机接收信号为

s(t)=AP(t)ej(ω0t+θ0)+Ad·

AP(t-τd)ej(ω0t+θ0+θd)

(2)

卫星多径导致伪码测距观测量偏离的案例中，主要是之前的QPSK调制体制[1-2]，不涉及二进制偏移载波(BOC)调制体制与副载波。若相关延时为τ，那么信号归一化后的自相关函数有

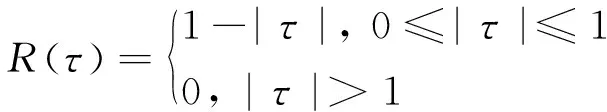
(3)

本处选用经典的码鉴相器(相干鉴相器与非相干鉴相器)[7]开展仿真工作，d为本地超前码和滞后码超前滞后值为相关器间距。经计算，多径导致的相干鉴相器伪码测距偏差为[8]

(4)

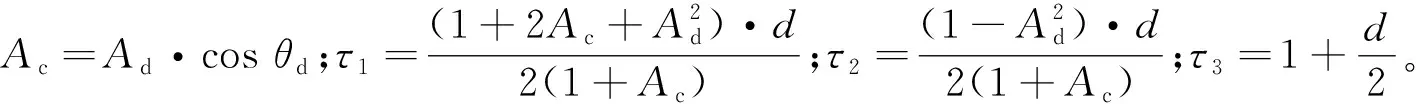
多径导致的非相干鉴相器伪码测距偏差为[8]

(5)

Ae，Af，Ag与Ah的具体描述有

(6)

卫星导航系统基带部分一般采用直接序列扩频(DSSS)调制，即产生一组双极性波形的伪随机噪声码，在波形转换之间的最小时间间隔通常被称为码片(chip)，码片的倒数称为码片速率，简称码速率(chips per second，c/s)。

若导航信号扩频码码速率为2.046 Mc/s，接收带宽20 MHz，本地相关器间距d为0.5码片，那么多径幅度是主径的1/5、3/10与1/2情况下，多径跟踪误差曲线如图1所示。

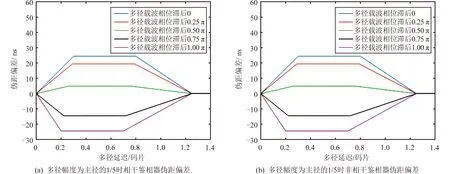
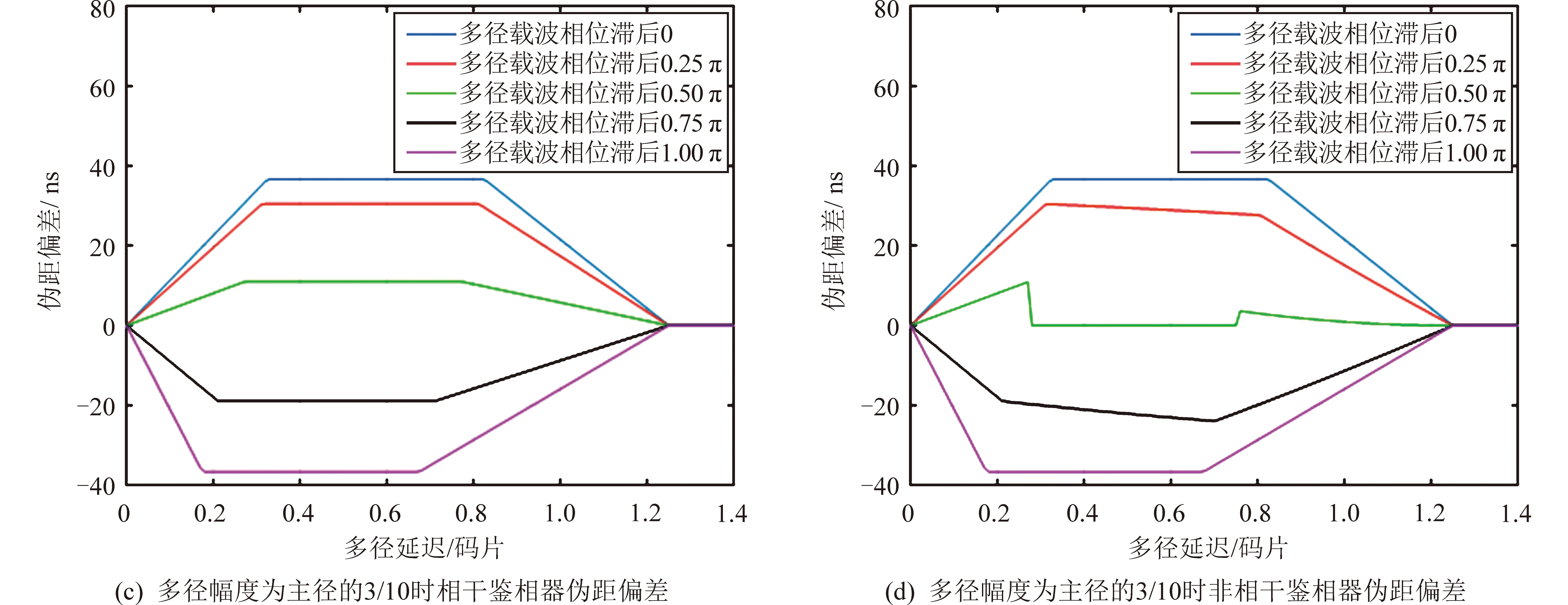
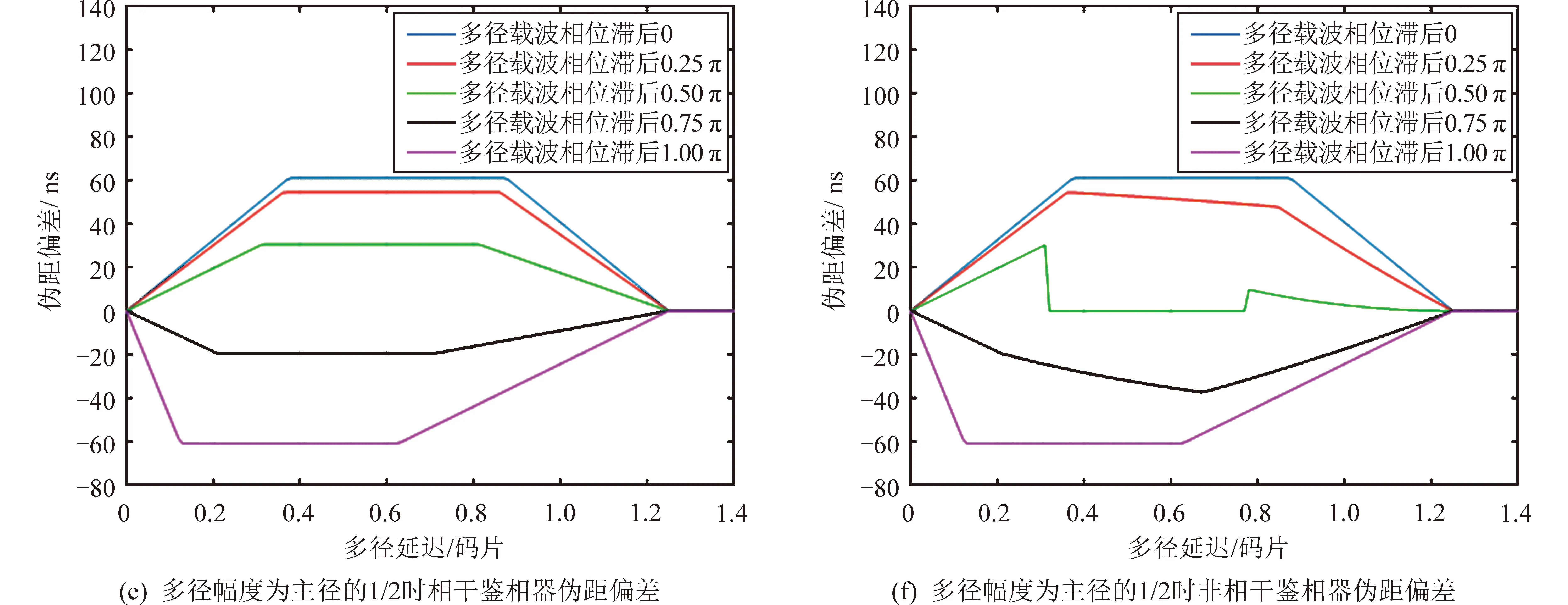
图1 多径效应对伪码测距鉴相误差的影响Fig.1 The pseudorange measurement error curve caused by multipath effect

根据仿真结果可知，多径会导致接收机伪码测距观测量与实际值发生偏离，多径幅度衰减Ad=0.2时，最大可能会存在24.4 ns的伪码测距观测量误差；多径幅度衰减Ad=0.3时，最大可能会存在36.7 ns的伪码测距观测量误差；多径幅度衰减Ad=0.5时，最大可能会存在61.1 ns的伪码测距观测量误差。接下来需分析当多径来源于卫星自身时，如何能够达到文献[1]所描述的北斗卫星伪码测距观测量偏离载波相位观测量1.5 m的异常程度。

2 卫星自身多径作用机理及影响分析

以GPS为例[9]，一种典型的导航卫星有效载荷射频链路框图如图2所示。由功能模块A和功能模块B组成。功能模块A包含导航任务数据单元、L频段发射机，功能模块B包含功率放大器、互扰清除装置与天线耦合器网络。功能模块A中传输的信号具备为基带频率与小功率的特性，其多径效应可以忽略，重点考虑功能模块B。

图2 典型的导航卫星射频链路框图Fig.2 Typical setup of a radio navigation signal generator on satellite

功能模块B中，导航信号合路后按照90.5%和9.5%的比例馈入天线耦合器网络输入端口1和2，1输入端口对应天线阵列内圈阵元信号输出； 2输入端口对应天线阵列外圈阵元信号输出。若多径发生在功能模块B的前两个部分，那么对各路天线阵元而言多径信号传输射频路径相同，即等效为各天线阵元同时叠加相同多径幅度衰减与延迟的干扰信号，不影响天线阵元时延一致性。因此本文重点分析天线耦合器网络，尤其是1与2输入端口连接处存在多径时，对伪码测距观测量的影响。

根据图1仿真结果，多径会使各天线阵元伪码测距观测量与实际值发生偏离，当端口1或端口2处存在多径时，就会使导航天线内圈阵元或外圈阵元时延观测量与实际值不一致，进而导致天线阵面内外圈间时延不一致。

北斗卫星、GPS卫星与GLONASS等卫星的有效载荷天线实现方案基本一致，均采用螺旋单元阵列生成覆球波束。为便于问题说明，本文按照GPS Block IIR导航载荷天线进行建模与仿真工作[10]，天线由12个阵元组成，其几何构型示意如图3(a)所示。其中内圈半径Rin为18.03 cm，功率占比为90.5%，载波相位θin；外圈半径Rout为47.50 cm，功率占比9.5%，载波相位θin+180°。

GPS卫星的轨道高度为20 187 km，地球半径按照6371 km计算，则卫星距波束中心点的距离为25 783 km。星地几何关系见图3(b)。

建立卫星俯角向量α=[α1α2…αN]，其中，N为俯角向量采样点数，根据星地几何关系及天线几何构型，计算得到阵元i与地球表面监测接收机之间的距离向量Ri的函数。

Ri(α)=[ri(α1)ri(α2)…ri(αN)], 1≤i≤12

(7)

将GPS L1信号(1575.42 MHz)作为信号源，监测接收机观察到的内外圈阵元信号如下

(8)

式中：c为电磁波在真空中的传播速度。

将信号进行合路，表达式如下

(9)

分别取ssum(α,t)的幅度及相位，绘制二者与卫星俯角向量的关系曲线，结果如图4所示。图4(a)为波束合成后天线各向卫星俯角下的增益，波束主瓣方向坐标为(13.88,2.10)和(-13.90,2.10)，波束星下点方向坐标为(0.03,0.00)。即波束主瓣方向偏离阵列法向的角度约为13.88°，相对于星下点的信号功率增益高约2.1 dB，与设计值一致；图4(b)为波束合成后天线各向卫星俯角下的载波相位，由图可知，波束主瓣范围内载波相位各向一致，亦与设计值一致[9-10]。

图4 GPS Block IIR天线L1频点方向图Fig.4 GPS Block IIR antenna pattern of L1 signal

之后就导航天线阵元间时延不一致对伪码测距观测影响进行仿真，若多径引起的内外圈时延偏差为τ′，那么地面天线接收信号的表达式为

(10)

波束中心点时，αM=13.88°；波束星下点时，αI=0°。代入式(10)，得到波束中心点接收信号ssum(αM,t,τ′)与波束星下点接收信号ssum(αI,t,τ′)。

利用式(4)所示的相干鉴相器对二者进行接收处理，得到波束中心点伪码测距测量值R(αM,τ′)和波束星下点伪码测距测量值R(αI,τ′)，二者相减即得到波束中心点与星下点之间伪码测距测量值之差：

ΔR(τ′)=R(αM,τ′)-R(αI,τ′)

(11)

仿真τ′与ΔR(τ′)之间的关系，如图5所示。

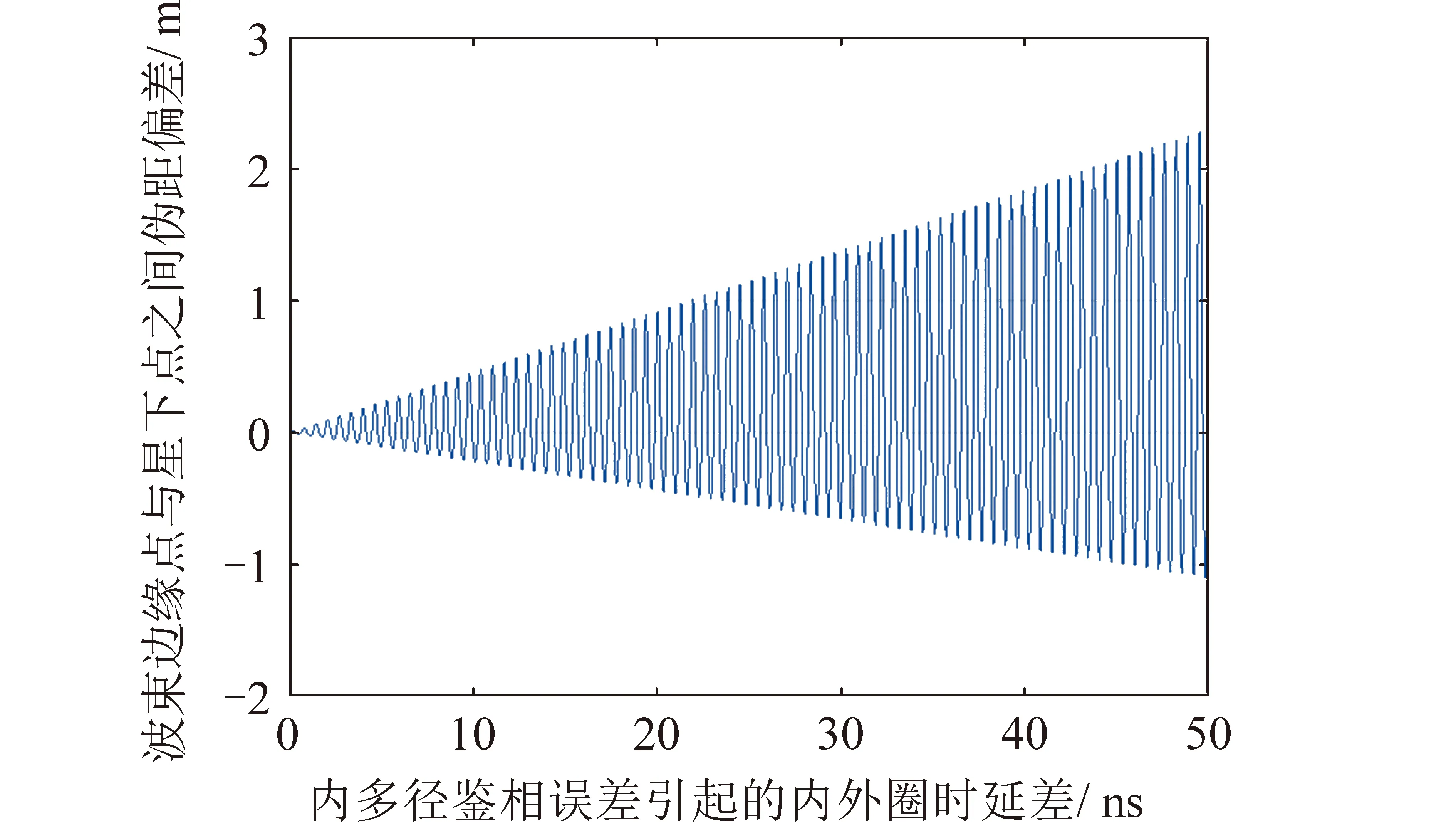
图5 天线阵元内外圈时延偏差和波束中心点星下点间伪码测距偏差之间的关系Fig.5 Relationship between pseudorange measurement divergences and the inner-outer ring delay consistence

图5中，横坐标为天线阵元内圈时延与外圈时延之间的差值(正常应无差值，各阵元时延一致)，纵坐标为导航信号波束中心点与星下点之间伪码测距的偏差。根据图3(b)所示，导航信号波束中心点对应地面测试天线仰角为0的场景，星下点对应地面测试天线仰角为90°的场景，图5主要仿真这两种情况下伪码测距观测量差异。根据仿真结果，当天线阵元时延一致的情况下，两种场景伪码测距观测量差异为0，符合设计状态。而随着天线阵元时延偏差逐渐变大，两种场景伪码测距观测量差异的包络也在逐步扩大，超过30 ns时，偏差会达到1.5 m的量级，与文献[1]描述的现象一致。此时不同仰角伪码测距观测量偏差仿真结果与文献[1]描述结果比对情况如图6所示。图6(a)和(b)为文献描述的GPS、Galileo的伪码测距观测量偏差统计结果，图6(c)为文献描述北斗卫星4种接收机 (型号为：Javad公司 的TRE_G3T SIGMA, Trimble公司的NetR9, Septentrio公司的PolaRx4和 Leica公司的GR25) 伪码测距观测量偏差测量结果，图6(d)为模型伪码测距偏差仿真结果。图6中，横坐标为地面测试天线仰角，纵坐标多径组合观测(MP)值测量或仿真结果。比对结果表明仿真结果与文献对北斗卫星伪码测距测量偏差的描述高度一致。

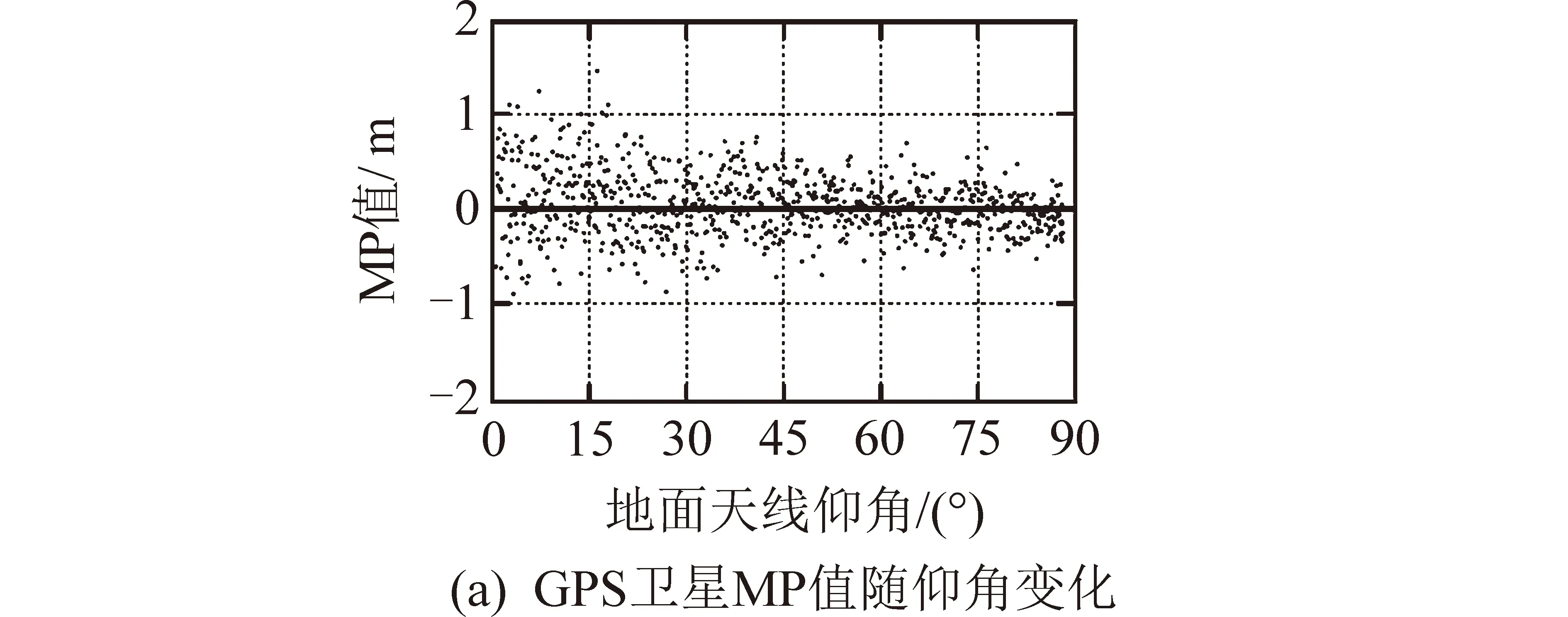
图6 仿真结果与文献观测结果比对情况Fig.6 Comparison of simulation results with literature observations

综上所述，天线内外圈阵元间时延一致性是评估卫星是否存在文献[1]所描述的在轨伪码测距观测量异常变化的关键指标，当天线内外圈阵元之间时延一致性差异超过10 ns的时候，会观察到波束中心点与星下点之间伪码测距观测量存在明显偏差，当天线内外圈阵元之间时延一致性差异超过30 ns的时候，偏差会达到文献[1]描述的1.5 m量级。

由此可见，在导航卫星有效载荷设计阶段，需保证天线各阵元间时延一致性。各单机集成完毕后，应该对射频链路各器件，尤其是天线耦合器网络的散射参数 (S参数)进行确认，确保不会出现由于阻抗失配导致信号反射，引入多径及相位畸变。

同时，在导航有效载荷工厂测试阶段，必须确认天线阵元间伪随机码相位一致性，尤其是内外圈阵元之间的一致性。可以利用数据采集器对天线阵列各阵元耦合口信号进行采集，相干鉴相处理后得到各阵元时延测试结果，测试要求一致性在10 ns以内，这样可以有效规避在轨伪码测距观测量异常变化的问题，提高导航系统的定位精度。

3 结论

本文针对国外文献[1]所描述的北斗卫星在轨伪码测距测量值与载波相位测量值之间异常偏离的问题，开展机理分析及仿真计算，并给出了可能造成该问题的原因。分析结果表明：

(1)就卫星自身而言，若导航载荷天线内外圈阵元之间时延一致性超过10 ns，会引发显著的伪码测距观测量异常偏离载波相位测量值的现象，当天线内外圈阵元之间时延一致性差异超过30 ns的时候，必然会导致文献[1]描述的1.5 m量级的伪码测距观测量偏差。

(2)在导航卫星有效载荷天线设计过程中，除了考虑主瓣波束范围内天线阵元载波相位是否符合设计值，还要考虑伪随机码相位的一致性；

(3)天线内外圈阵元间时延一致性是必须考虑与考核的关键指标，应在卫星出厂前予以确认。