悬挂式单轨最小平面曲线半径及缓和曲线长度研究

谭小波

(西南交通大学土木工程学院，四川成都 610031)

悬挂式单轨，又被称为“空铁”，最早在德国建成，近年来在我国兴起。由于悬挂式单轨具有建设快、占地少、造价低、环境适应能力强、视觉效果好等优势，因此在我国具有很大的发展潜力[1-3]。

在国外，只有德国和日本具有成熟的悬挂式单轨运营经验，国内的悬挂式单轨建设脚步越来越快，但是尚无统一的技术标准和设计规范。因此，研究悬挂式单轨线路设计参数十分重要。本文借鉴传统铁路设计理论和经验，从运行安全性、乘客舒适性的角度，对悬挂式单轨最小平面曲线半径和缓和曲线长度进行研究。

1 悬挂式单轨结构特点

悬挂式单轨铁路是单轨铁路的一种，其轨道在上、车辆在下，车体悬挂在轨道梁下方。悬挂式单轨主要由轨道梁、车辆、车站、道岔、通信系统、供电系统等部分组成，悬挂式单轨车辆可分为转向架、悬挂装置和车体[4-5]。悬挂式单轨基本结构如图1所示。

图1 悬挂式单轨基本结构

悬挂式单轨的主要结构特点有：(1)悬挂式单轨的转向架位于钢制的、开口向下的轨道梁内，一般不存在脱轨可能。(2)车体与转向架之间通过牵引悬挂装置连接，牵引悬挂装置包括中心销、横摆减振器等。列车通过平面曲线时，横摆减振器会在一定程度上限制车体的横向偏转。(3)列车通过平面曲线时，车体会发生偏转，能在一定程度上抵消行驶时产生的离心力，因此不设超高。悬挂式单轨车体的偏转如图2所示。

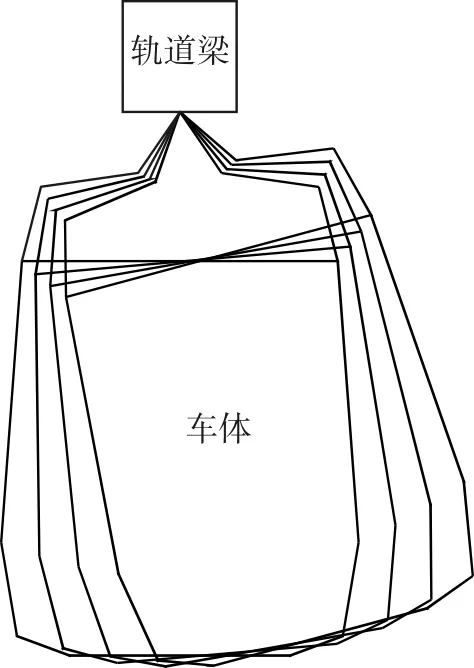
图2 悬挂式单轨车体偏转

2 悬挂式单轨最小平面曲线半径

2.1 最小平面曲线半径设计原则

在传统铁路中，列车通过曲线时，如果平面曲线半径R过小，则速度V产生的离心加速度大于外轨超高产生的向心加速度，由此出现未被平衡的离心加速度。在传统铁路中，未被平衡的离心加速度用欠超高hq来表示。在传统铁路参数设计中，最小平面曲线半径的设计原则是：保证列车以最高速度Vmax通过时，欠超高hq不超过允许值hqy，以保证旅客舒适度[6]。

对悬挂式单轨而言，当悬挂式单轨通过平面曲线时，车体在离心加速度的作用下会发生横向摆动，车体向曲线外侧偏转一定角度。若车体与转向架之间完全无约束，则车体的偏转角度完全由离心力决定，此时车体重力在向心方向的分力正好等于离心力，不存在未被平衡的离心加速度。然而在实际情况中，由于车体与转向架之间存在横向减振器、摩擦阻力等，使得车体的偏转角度达不到平衡离心力所需的角度，此时就产生了未被平衡的离心加速度。悬挂式单轨的参数设计方法参考传统铁路，但由于悬挂式单轨不设超高，在其最小平面曲线半径的设计原则中，应把“欠超高不超过允许最大欠超高”改为“未被平衡的离心加速度不超过允许最大值”。同时，在悬挂式单轨中，若平面曲线半径R过小，则速度V产生的过大离心力会使车体横向偏转角过大，从而影响乘客舒适度。所以在悬挂式单轨最小平曲线半径的设计原则中，还应考虑车体的最大偏转角。

综上所述，悬挂式单轨最小平面曲线半径的设计原则为：(1)保证列车以最高速度Vmax通过时，未被平衡的离心加速度不超过允许最大值。(2)保证列车以最高速度Vmax通过时，车体最大偏转角不超过允许值。

2.2 最小平面曲线半径公式推导

在悬挂式单轨中，未被平衡的离心加速度可以表示为：

式中：aq为未被平衡的离心加速度(m/s2)；V为悬挂式单轨运行速度(km/h)；R为经过的平面曲线半径(m)；g为重力加速度值，取9.8m/s2；θ为车体横向偏转角(rad)。

设未被平衡的离心加速度允许值为aqy，车体横向最大偏角允许值为θy。由于aq≤aqy，θ≤θy，所以若已知aqy和θy的大小，则最小平面曲线半径可以表示为：

式中：Rmin为悬挂式单轨最小平面曲线半径(m)。

由该公式可知，只需得到aqy和θy的取值大小，带入该公式，即可得到悬挂式单轨最小平面曲线半径Rmin与其运行速度V之间的关系。

2.3 最大偏转角允许值

在传统铁路中，为了保证列车不内向倾覆，同时保障乘客舒适，需要限制外轨超高的最大值。外轨超高越大，列车的偏转角越大，乘客越不舒适。对比可知，悬挂式单轨的最大偏转角与传统铁路中的外轨最大超高类似。同时，悬挂式单轨由于对车辆结构和车内设施进行了优化，且运行的速度比较一致，从而提高了舒适性，这两点与传统铁路中的客运专线类似。所以可参考客运专线的外轨超高允许值来计算悬挂式单轨的最大偏角允许值。

查阅相关资料[7]，客运专线实设超高最大允许值取180 mm，可将该值换算为客运专线的最大偏转角，然后用于悬挂式单轨中。在客运专线中，由几何关系：

式中：θy为最大偏转角允许值(rad)；hy为客运专线实设超高最大允许值(mm)；S为两根钢轨轨头中心线之间的距离(mm)。

带入hy=180 mm，S=1 500 mm(标准轨)，算得最大偏转角θy=6.892°=0.12 rad。

2.4 未被平衡的离心加速度允许值

根据我国城市轨道交通设计运营经验，未被平衡的离心加速度允许值取0.4 m/s2比较合适[8]。本文建议在悬挂式单轨中aqy取0.4 m/s2。

2.5 最小平面曲线半径取值

将θy=6.892°=0.12 rad和aqy=0.4 m/s2带入Rmin的计算公式，并取g=9.8 m/s2，得悬挂式单轨最小平面曲线半径：

式中，Rmin为悬挂式单轨最小平面曲线半径(m)；V为悬挂式单轨运行速度(km/h)。

建议悬挂式单轨最小平面曲线半径以该式计算，同时，为了测设、施工和养护的方便，建议把结果进整为10 m的整倍数，得悬挂式单轨不同设计速度下的最小平面曲线半径值，如表1所示。

表1 悬挂式单轨最小平面曲线半径值

实际施工中，如果遇到特殊条件，导致悬挂式单轨平面曲线半径取值困难，可经过技术经济比选后在上表的基础上选择适当较小的值。

3 悬挂式单轨缓和曲线长度

3.1 缓和曲线长度设计原则

在传统铁路中，缓和曲线长度影响行车安全和旅客舒适，在拟定缓和曲线长度标准时，根据下列三个条件各自计算并取其中的较长者[6]。条件一：超高顺坡不致使车轮脱轨；条件二：超高时变率不致使旅客不适；条件三：欠超高时变率不致使旅客不适。

根据传统铁路设计经验，当列车低速运行时，上述条件一算出的缓和曲线最长，起控制作用；当列车中速运行时，上述条件二起控制作用；当列车高速运行时，上述条件三起控制作用。

对悬挂式单轨而言，由于其不设超高，且其走行部分包裹在轨道梁内，不存在脱轨问题，所以拟定其缓和曲线长度时无需考虑上述条件一。悬挂式单轨经过缓和曲线时车体会逐渐发生横向偏转，称其横向偏转的角速度为“倾斜时变率”[9]。悬挂式单轨在直线上横向偏转角为零，在圆曲线上横向偏转角不为零，若缓和曲线长度过短，则经过缓和曲线所用时间(过渡时间)较少，势必导致倾斜时变率过大，影响旅客舒适度。可以发现，这里的倾斜时变率类似于传统铁路中的超高时变率，两者都刻画了车体偏转的速度，两者过大都会造成旅客不舒适。所以在拟定悬挂式单轨缓和曲线长度时，参考上述条件二，并把“超高时变率不致使旅客不适”改为“倾斜时变率不致使旅客不适”。

同时，悬挂式单轨在直线上未被平衡的离心加速度为零，在圆曲上未被平衡的离心加速度不为零。则未被平衡的离心加速度在过渡的缓和曲线上越来越大，称其变化的速度为“未被平衡的离心加速度时变率”。若缓和曲线长度过短，则经过缓和曲线所用时间(过渡时间)较少，势必导致未被平衡的离心加速度时变率过大，影响旅客舒适度。如前文所述，在传统铁路中，未被平衡的离心加速度用欠超高来表示，那么上述条件三中的“欠超高时变率”实际上表示的应该是“未被平衡的离心加速度时变率”。所以在拟定悬挂式单轨缓和曲线长度时，参考上述条件三，并把“欠超高时变率不致使旅客不适”改为“未被平衡的离心加速度时变率不致使旅客不适”。

综上所示，悬挂式单轨最小缓和曲线长度的设计原则为：(1)倾斜时变率不致使旅客不适。(2)未被平衡的离心加速度时变率不致使旅客不适。

由于此处的原则1、2分别继承于传统铁路缓和曲线设计中的条件二、三。所以参考传统铁路设计经验，当速度较低时，应该是原则(1)算出的缓和曲线较长，起控制作用；当速度较高时，应该是原则(2)起控制作用。而悬挂式单轨的设计速度基本在50～70 km/h，相对较低，此时原则(1)起控制作用。于是在计算悬挂式单轨最小缓和曲线长度时，先以原则(1)计算，然后把原则(1)的计算结果带入原则(2)检验，若检验通过，则说明该结果同时满足原则(1)、(2)，以该结果进行悬挂式单轨最小缓和曲线取值是合理的。

3.2 基于倾斜时变率的缓和曲线长度计算

3.2.1 基于倾斜时变率的缓和曲线长度公式推导倾斜时变率可以表示为：

式中：w为悬挂式单轨倾斜时变率(rad/s)；θ为车体横向偏转角(rad)；t为通过缓和曲线所用时间(s)。

其中：

式中：L为悬挂式单轨缓和曲线长度(m)；V为悬挂式单轨运行速度(km/h)。

所以倾斜时变率w可表示为：

设最大倾斜时变率允许值为wy，由于w≤wy，若已知wy的大小，则悬挂式单轨缓和曲线最小长度可以表示为：

式中：Lmin为悬挂式单轨缓和曲线最小长度(m)。

其中，需要对车体横向偏转角θ进行计算。如前文所述，在实际情况中，由于车体与转向架之间存在横向减振器、摩擦阻力等，使得车体的偏转角度达不到平衡离心力所需的角度，即：

由于各厂家生产的悬挂式单轨车辆系统参数不同，且各参数对θ的影响机制复杂，导致难以得到一个普遍适用的、准确的θ的解析表达式。但是从实用性和安全性的角度来看，求Lmin不必先得到θ的准确表达式，可以对θ进行放缩，得到θ的一个适当偏大的值，由此计算出的Lmin也是适当偏大、偏安全的，可满足实际需要。即令：

且车体横向偏转角θ一般很小，所以有：

θ≈tanθ

于是得到θ的近似表达式：

如前文所述，该表达式求出的θ来计算Lmin是偏安全的，所以在本文中用此方法近似求θ是科学的。

将θ的表达式带入Lmin，得：

3.2.2 最大倾斜时变率允许值

如前文所述，悬挂式单轨中的倾斜时变率类似于传统铁路中的超高时变率，那么就可以参考传统铁路中的超高时变率允许值来拟定悬挂式单轨中的最大倾斜时变率允许值。

在传统铁路中，超高时变率表示为:

式中：h为传统铁路中圆曲线上的外轨超高(mm)；t为通过缓和曲线所用时间(s)。

由几何关系：

h=S·sinθ

式中：S为两根钢轨轨头中心线之间的距离(mm)，在标准轨中S=1 500 mm；θ为车体横向偏转角(rad)。

设超高时变率允许值为f，当：

反解出：

将t带入w，得：

式中，wy为最大倾斜时变率允许值(rad/s)。

我国在制定相关标准时，超高时变率允许值f的取值为：城际铁路，一般条件下取28 mm/s，困难条件下取35 mm/s[10]；客运专线铁路，良好条件下取25 mm/s，一般条件下取28 mm/s，困难条件下取31 mm/s[11]；地铁(其最高设计速度为100 km/h)，f取40 mm/s[12]。

可以发现f的变化规律：随着设计速度降低，f逐渐变大，换算出的wy自然也相应变大。对于悬挂式单轨，国内不同厂家生产的悬挂式单轨车辆的设计速度基本在50～70 km/h，比地铁的设计速度还低，所以本文建议以f=45 mm/s进行wy的换算。带入wy的计算公式，得：

3.2.3 基于倾斜时变率的缓和曲线长度取值

将wy=0.03 rad/s带入Lmin的计算公式，并取g=9.8 m/s2，得悬挂式单轨最小缓和曲线长度：

式中：Lmin为悬挂式单轨最小缓和曲线长度(m)；V为悬挂式单轨运行速度(km/h)；R为平面圆曲线半径(m)。

建议悬挂式单轨最小缓和曲线长度以该式计算，同时，为了测设、施工和养护的方便，建议把结果进整为5 m的整倍数，最小取10 m。得悬挂式单轨不同设计速度下常用曲线半径的缓和曲线长度值，如表2所示。

表2 悬挂式单轨缓和曲线长度

实际施工中，如果遇到特殊条件，导致悬挂式单轨缓和曲线取值困难，可经过技术经济比选后在上表的基础上选择适当较小的值。

3.3 基于未被平衡离心加速度时变率的缓和曲线长度检算

设未被平衡离心加速度时变率为β，设未被平衡离心加速度时变率的允许值为βy。悬挂式单轨的乘客乘车环境与地铁的乘车环境类似，所以参考我国地铁设计规范[12]，取βy=0.3 m/s3。由：

式中：β为未被平衡离心加速度时变率(m/s3)；aq为未被平衡的离心加速度(m/s2)；t为经过缓和曲线所用时间(s)；L为缓和曲线长度(m)；V为行车速度(km/h)。

可得：

在满足平面曲线半径取值要求的情况下，将上文基于倾斜时变率的缓和曲线长度值带入β计算公式，若由此算出的β最大值βmax满足：

βmax<βy(βy=0.3m/s3)

则检算通过。

其中，当aq=0.4 m/s2(在满足平面曲线半径取值要求的情况下，取aq的最大值)时，β取得最大值βmax。由前文：

所以，当aq=0.4 m/s2时，必有：

即：V2>5.184R(β取得最大值βmax的必要条件)。

此时，将上文基于倾斜时变率的缓和曲线长度值带入β计算公式，有：

(其中V2>5.184R)<0.3

说明基于倾斜时变率的缓和曲线长度值同时也满足未被平衡的离心加速度时变率不超限，检算通过。实际应用中，可以用基于倾斜时变率的缓和曲线长度计算公式来计算悬挂式单轨缓和曲线长，表2的取值是科学的。

4 结论

(1)根据传统铁路经验，悬挂式单轨车辆最大偏转角不宜大于6.892°，最大未被平衡离心加速度取0.4 m/s2。(2)得到了悬挂式单轨最小平面曲线半径计算公式，不同设计速度下悬挂式单轨的最小平面曲线半径值如表1所示。(3)根据传统铁路经验，悬挂式单轨最大倾斜时变率不宜大于0.03 rad/s，最大未被平衡离心加速度时变率取0.3 m/s3。(4)得到了悬挂式单轨最小缓和曲线长度计算公式，不同设计速度下常用曲线半径的缓和曲线长度值如表2所示。