小电阻接地系统高灵敏性零序电流保护

李海锋，陈嘉权，曾德辉，梁远升，王 钢

华南理工大学 电力学院，广东 广州 510641)

0 引言

随着城市的快速发展，城市用地日益紧张，电缆线路在配电网中所占的比例也日渐增大。相较于消弧线圈接地方式，小电阻接地方式具有能够有效限制弧光接地过电压以及可及时切除故障线路等众多优点[1]，更适用于电缆居多的大中型城市配电网，比如：北京、上海、深圳的配电网均部分采用了小电阻接地方式，广州供电局更是全部采用小电阻接地方式[2]，广东电网也逐步将其10 kV配电网全部改为小电阻接地方式。然而，由于配电网馈线所处的环境复杂，容易发生单相经高阻接地故障，其过渡电阻可达上千欧，如广州配电网发生的一例高阻接地故障中，实测的接地电阻高达1 000 Ω[3]。目前针对馈线单相接地故障主要采用阶段式零序电流保护方案，而高阻接地故障主要依靠零序Ⅱ段动作，但是为了躲开区外故障时流过本线路的对地电容电流值[3]，其对于区内经过渡电阻的接地故障灵敏性较差，可耐受的过渡电阻值一般为100 Ω左右，无法切除高阻接地故障。虽然高阻接地故障的故障电流较小，但若任其长期存在，势必会对设备的绝缘造成很大的威胁，继而引发诸如相间故障等更为严重的故障，扩大故障范围；同时，故障点的过电压以及电弧产生的高温都会造成人身安全问题，所以高阻接地故障的危害不容忽视。

单相高阻接地故障由于故障电流小，且类型复杂多样，接地电阻可能是线性的也可能是非线性的，所以一直以来是配电网难以解决的实际工程问题，吸引了众多学者的关注和研究。然而目前大部分研究都是针对小电流接地系统，其原理主要集中在利用谐波或者暂态能量方面[4-7]。由于接地回路存在本质差异，这些方法是否适用于小电阻接地系统尚不明确，而具体针对小电阻接地系统的研究则较少。

文献[8-9]对高阻接地故障的非线性特征进行研究，并提取其时域故障特征。其中，文献[8]提出了一种利用伏安特性反映故障电阻非线性特征的检测算法，但是无法识别非线性特征不明显的故障。文献[9]通过观察零序电流的波形，提出了一种基于波形凹凸性的检测算法，但其会受各种噪声的影响。由于基于暂态量的算法较为复杂，且可靠性不高，而基于稳态量的算法无疑是一种更具有实际工程意义的方法。目前也有采用零序功率方向保护元件的工程案例，但是其极性校验困难，且效果并不理想[10]。文献[11]根据保护安装处零序电流幅值与零序电压幅值成正比的关系，引入零序电压作为制动量，提出了一种比率制动的算法，但其定值整定较为复杂。另外，目前大部分研究只限于理论分析，其工程实用性还有待检验。

为此，本文同样利用零序电压可以反映过渡电阻大小的思路，在分析过渡电阻对小电阻接地系统各零序分量的影响及其相互关系的基础上，提出了一种基于零序电压幅值修正的高灵敏性零序电流保护方案。通过仿真验证了本文方法的有效性，并利用RTDS对保护装置进行了数字动模仿真测试。

1 单相接地故障特征分析

图1为小电阻接地系统单相接地故障的示意图。图中，接地小电阻Rg接在曲折变压器的中性点上；N表示非故障线路；F表示故障线路；假设故障相为A相，故障点P带有过渡电阻Rf。

图1 小电阻接地系统单相接地故障示意图Fig.1 Schematic diagram of single-phase-to-ground fault in low-resistance grounding system

假设网络中各元件参数均为三相对称，则各序分量具有独立性。利用叠加定理并结合对称分量法可得故障点零序电流为：

(1)

其中，UfA为故障点P正常运行时的A相电压；Z+、Z-、Z0分别为从故障点P端口看进去的正、负、零序等效阻抗。

由于故障点到母线处的线路阻抗对稳态计算影响较大，而非故障线路以及故障点后的线路阻抗主要影响暂态过程，所以可忽略其影响，只保留故障点到母线处的线路阻抗。根据图1可以得到小电阻接地系统零序网络，如图2所示。图中，C1、C2、…、Cn分别为各非故障线路的对地电容；Cf和Cb分别为故障点前、后的线路对地电容；Lg为曲折变压器的零序电感；ZLf0为故障点到母线的线路零序阻抗；Ufa0为故障端口的零序等效电压源，其包含了过渡电阻的压降。由此可得零序等效阻抗为：

Z0=(Zp+ZLf0)∥Zq

(2)

Zp=Zzig∥{1/[jω(CN∑+Cf/2)]}

Zq=1/[jω(Cf/2+Cb)]

Zzig=3Rg+jωLg

其中，Zzig为曲折变压器支路阻抗；CN∑为健全线路对地电容之和。

图2 小电阻接地系统零序网络Fig.2 Zero-sequence network of low-resistance grounding system

1.1 故障线路零序电流分析

由零序网络可得故障线路零序电流IF0与故障点零序电流Ifa0的关系为：

(3)

其中，b为比例系数。

为了简化分析，认为正、负序等效阻抗相等，且由于系统阻抗与主变漏抗之和比负载阻抗小得多，可进一步忽略负载阻抗。考虑到线路对地容抗远大于系统阻抗与主变压器漏抗之和，所以可近似有：Z+=Z-jωL1+ZLf+(L1为换算到10 kV侧的系统等效电感和主变漏感之和，ZLf+为故障点到母线的线路正序阻抗)；而考虑对地容抗也远大于曲折变压器支路阻抗，则有Z0≈3Rg+jωLg+ZLf0。综上可得|b|≈1，即故障线路零序电流与故障点零序电流的大小近似相等。则联立式(1)—(3)可得：

(4)

其中，IF0、Ufa分别为IF0、Ufa的大小。

可见，由于L1、Lg、ZLf+和ZLf 0都较小，而Rg一般为10 Ω或12 Ω，当过渡电阻Rf较小时，单相接地故障下的零序电流IF0将较大，即故障线路具有明显的故障特征，这是小电阻接地系统的优点之一。但是随着过渡电阻Rf的增大，IF0将迅速地减小。不妨进行简单估算：取Rg为10 Ω，忽略L1、Lg、ZLf+和ZLf 0，当过渡电阻为100 Ω时，故障线路零序电流将小于20 A，此时现有的零序电流保护已经无法动作。

1.2 母线零序电压分析

结合零序网络和式(3)可得母线零序电压为：

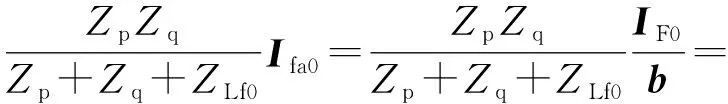
(5)

由式(5)可见，母线零序电压与故障线路零序电流成正比，即U0的大小U0与IF0随过渡电阻的增大会同比例地减少[11]，故可以通过U0来反映过渡电阻的大小。若将母线零序电压作为修正量，对测量所得的零序电流进行修正，即可大幅减弱过渡电阻的影响，具体推导如下。

首先对式(1)两端同时进行如下变换：

(6)

将式(5)代入式(6)可得：

(7)

其中，Z+h、Z-h、Z0h分别为线路首端故障时对应的正序、负序、零序等效阻抗。

显然式(7)的右边为发生金属性接地故障时的零序电流表达式。因此进一步考虑到式(3)的关系，可以构造如下修正系数：

(8)

其中，UpN为母线相电压。利用该修正系数对故障线路和非故障线路的零序电流进行修正，则有：

(9)

(10)

其中，bh为故障线路首端发生故障时对应的比例系数；Ci为第i回非故障线路的对地电容。

由式(9)和(10)可见，对于经过渡电阻接地故障，经过上述修正后，故障线路零序电流以及各非故障线路的零序电流均与故障线路首端发生金属性接地故障时的情况完全相同，即不再受过渡电阻的影响。以此为基础，本文提出一种基于零序电压幅值修正的高灵敏性馈线零序电流保护。

2 高灵敏性零序电流保护

2.1 基本原理

现有的零序电流保护在过渡电阻较小时具有可靠性高的优点，其保护动作整定值的物理意义明确。因此，可以在保持现有的馈线零序电流保护整定值的基础上，对测量所得的零序电流进行如下修正：

(11)

(12)

其中，I0.unb为零序电流互感器可能出现的最大不平衡值，其与零序电流互感器的传变特性以及系统不对称运行时出现的不平衡电流有关；K为修正系数；UlN为母线额定线电压。

由于零序等效阻抗比正序、负序等效阻抗大得多，所以K受系统运行方式的影响较小。在实际计算中，修正系数可以采用近似参数进行计算，即Z+h和Z-h只考虑10 kV侧的系统等效感抗与主变漏抗之和，其中系统等效感抗可考虑最小运行方式下的值，而Z0h只考虑曲折变压器支路阻抗，此时有：

(13)

进一步考虑到正负序等效阻抗远小于零序等效阻抗，则修正系数可简化为：

(14)

(15)

图3 修正系数变化曲线Fig.3 Varying curve of correction coefficient

由前文的分析可得，修正后的故障线路零序电流以及各非故障线路零序电流均与故障线路首端发生金属性接地故障时的情况相同，所以现有的保护动作整定值仍有效，从而提高了保护对高阻接地故障的灵敏性。

2.2 保护算法流程图

图4为本文所提的高灵敏性零序电流保护的算法流程图。图中，为了与实际工程习惯相配合，零序分量均为3倍零序值，后同；3I0.set为高灵敏性馈线零序电流保护动作整定值；3U0.set为设置的零序电压下限值，用于防止测量所得的零序电压过小导致保护误动作，其与电压互感器以及系统不对称程度有关；TL.set为计时设定值。

图4 高灵敏性零序电流保护算法流程图Fig.4 Flowchart of high sensitive zero-sequence current protection algorithm

2.3 整定原则

本文所提的高灵敏性零序电流保护算法中有4个参数需要整定，下面分别对其设置原则进行讨论。

a. 零序电流保护动作整定值3I0.set。

3I0.set按照现有的馈线零序电流保护的整定原则进行整定，其要躲开区外故障时本线路流过的电容电流值，即：

3I0.set=KrelICl

(16)

其中，Krel为可靠系数，一般取1.5～2.0；IC为单位长度对地电容电流，按照工程惯例，一般取为2 A/km；l为线路长度。

b. 零序电压下限值3U0.set。

3U0.set的取值需要考虑系统正常运行状态下的不平衡电压问题。图5为小电阻接地系统正常运行时的简化示意图。由图可得小电阻接地系统正常运行下的中性点电压为：

(17)

(18)

其中，Kc为系统全部出线的不对称度；α为位移因子，α=ej120°。

图5 小电阻接地系统正常运行简化示意图Fig.5 Simplified schematic diagram of low-resistance grounding system under normal operation

架空线路中，Kc的大小通常为0.5%～1.5%，偶尔有大于等于2.5%的情况；电缆线路中，Kc的大小约为 0.2%～0.5%[12]。一般情况下，10 kV线路的供电半径在15 km以内。假设系统线路总长为105 km(带7条15 km馈线)，则ω(CA+CB+CC)为0.036 6 S(CA、CB、CC取值参见附录中表A1的零序电容参数)，考虑到Kc的大小取为2.5%以及Rg=12 Ω，则由式(17)可计算得UN的大小为58 V，即系统在正常运行状态下的最大不平衡电压3U0为174 V。

现场采集母线零序电压一般采用电压互感器的开口三角绕组，而正常运行时开口三角绕组的不平衡电压3U0约为1 V[13]，换算至一次侧即为174 V左右，与上述计算结果相同，所以建议3U0.set取174 V。

c. 零序电流互感器最大不平衡值3I0.unb。

3I0.unb的取值需要考虑系统不对称运行工况下可能出现的不平衡电流、线路参数不平衡以及零序电流互感器传变特性等问题。现场采集零序电流的方式有2种：一种是通过专用的零序电流互感器采集，另一种则是通过采集三相电流然后经信号处理后得到。由于相电流互感器的变比较大，且三相电流互感器间的传变特性难免存在一定的差异，所以由相电流互感器采集得到的零序电流一般误差较大，不太适用于高阻检测这种对零序电流测量精度要求较高的场合，而专用零序电流互感器的测量精度高，且在不对称运行工况下的不平衡值也相对较小，所以建议使用专用零序电流互感器。

由前文的计算可得小电阻接地系统的最大不对称度大小|Pasy|为1%，则由图5可得线路的不平衡电流为：

3Iunb=(Ki+Pasy)jω(CA+CB+CC)EA

(19)

其中，Ki为第i条线路的不对称度。考虑线路最长为30 km，对地电容电流为2 A/km，其不对称度大小|Ki|取为2.5%，且Ki与Pasy同向，则可得最大不平衡电流为2.1 A。考虑到可靠度为2，建议3I0.unb取为4.2 A。

d. 计时设定值TL.set。

TL.set的取值需要考虑保护之间的配合问题，本文所提保护算法用作后备保护时，可与现有的零序过流Ⅰ段相配合，其延时值可与现有的零序过流Ⅱ段相同，无需重新设定。

3 仿真分析

仿真所采用的10 kV小电阻接地系统如图1所示，其中曲折变压器按照其原理结构搭建了相应的PSCAD模型[14]，4条电缆馈线按照其尺寸结构[15]搭建了相对应的频变模型，电气参数见附录中的表A1。

表1 经线性过渡电阻接地故障的仿真结果及保护动作情况Table 1 Simulative results and protection operation of grounding fault with linear transition resistance

电弧接地故障的形式为一线性电阻Rf和非线性电弧电阻Rarc相串联。电弧模型采用控制论电弧模型，其为Mayr电弧模型的改进版，电弧方程如下：

图6 高灵敏性零序电流保护逻辑图Fig.6 Logic diagram of high sensitive zero-sequence current protection

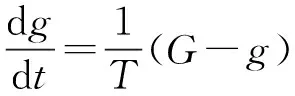
(20)

(21)

其中，g为电弧电导；T为时间常数；G为电弧稳定电导；β为比例系数；im为电弧电流峰值；larc为弧长；iarc为电弧电流；Vp为平均稳态电压梯度。

本文仿真中，控制论电弧模型的参数设置为：β=2.85×10-5；im近似取电弧故障点直接接地时的电流峰值[16]；起始电导g0=1 000 S；弧长larc统一设置为20 cm；平均稳态电压梯度Vp在电弧电流为1.4～24 kA时，一般取为15 V/cm[17]，但由于配电网发生单相接地故障时的电弧电流较小，而发生高阻接地故障时更小，所以本文仿真中Vp=17 V/cm。表2为电弧接地故障仿真结果。

上述仿真结果表明，本文所提保护方案对2种故障均能正确动作，且采用2种不同修正系数K′、K″后的修正效果与前文分析一致。可见，本文所提保护方案通过引入零序电压幅值对零序电流测量值进行修正，修正后的零序电流略小于故障线路首端发生金属性接地故障时的零序电流。与现有的馈线零序电流保护相比，本文所提保护方案大幅提高了保护可耐受的过渡电阻值(如在本算例中可耐受1 000 Ω的过渡电阻)。

表2 电弧接地故障的仿真结果及保护动作情况Table 2 Simulative results and protection operation of arc fault

大量仿真实验结果证明，选取不同的故障时刻、不同的故障点以及改变系统参数的情况下，本文所提保护方案均能正确动作。

4 基于RTDS的保护装置测试

4.1 高灵敏性零序电流保护功能实现

本次测试采用的保护装置是一台由本实验室团队研制的馈线测控保护一体化装置，其采用模块化设计，选用TI公司的OMAP-L138双核(DSP+ARM)处理器，可充分满足工业应用的高能效以及低功耗需求；该装置配置有大容量的RAM和高精度的AD转换芯片(AD7606)；该装置保护程序中的保护逻辑包含各种保护元件，且各元件可独立投退。装置的详细参数可参见文献[18]，本文不再赘述。

在该测试用保护装置的零序电流保护元件中嵌入本文所提出的高灵敏性零序电流保护功能。投入高灵敏性零序电流保护元件后，设定不平衡电流值I0SET_unb、零序电压下限值U0SET，当零序电流大于不平衡电流值且零序电压大于下限值时，对零序电流测量值进行修正，若修正值大于动作整定值，则发出跳闸信号并输出故障报告。图6为高灵敏性零序电流保护逻辑图。

4.2 RTDS装置测试

搭建第3节所述小电阻接地系统相应的RTDS模型，其中电压、电流互感器分别参考实际的10 kV电压、电流互感器的参数进行设置。保护装置设置在馈线3上，故障点设置在线路末端，通过不断增大线性过渡电阻值直至保护不动作，对现有的零序电流保护以及本文提出的高灵敏性零序电流保护进行装置测试。在本次测试中，修正系数只采用了实用型修正系数K″，且由于装置二次侧零序电流准确测量范围的最小值为0.1 A(一次侧为5 A)，所以3I0.unb=5 A， 其他参数设置同第3节，测试结果如图7所示。

图7 基于RTDS的保护装置测试结果Fig.7 Testing results of protection device based on RTDS

由图7可见，现有的零序电流保护若按线长整定，在本算例中可耐受的过渡电阻约为140 Ω，若按工程惯例统一设置为60 A[1-2]时其值更小，而本文提出的高灵敏性零序电流保护在发生经线性过渡电阻接地故障和电弧接地故障时均能正确动作，而且可耐受过渡电阻值可达1 000 Ω左右，极大地提高了保护对单相高阻接地故障的灵敏性，提高了配电网的安全稳定性。

5 结论

针对小电阻接地系统中现有的零序电流保护无法对单相高阻接地故障动作的现象，本文通过分析零序分量间的相互关系，发现母线零序电压与故障线路零序电流成正比，其可反映过渡电阻的大小，由此提出了一种高灵敏性零序电流保护。本文所提的保护方案结合了现有零序电流保护的优点，通过引入零序电压幅值信息对零序电流测量值进行修正，修正后各线路的零序电流与故障线路首端发生金属性接地故障时的情况相似，极大地提高了保护可耐受过渡电阻能力。基于PSCAD/EMTDC的仿真验证和基于RTDS的装置测试表明，本文所提保护方案物理意义明确，保护动作定值可沿用原有的阶段式零序电流保护整定原则，可将保护耐受过渡电阻能力提高到1 000 Ω左右；且算法基于工频量，易于实现，具有很好的工程应用前景。

附录见本刊网络版(http:∥www.epae.cn)。