基于机会约束规划的家庭用电设备负荷优化调度方法

曾 博，蒋雯倩，杨 舟，李 刚

广西电网有限责任公司电力科学研究院，广西 南宁 530023)

0 引言

随着智能电网的发展，电力用户将作为可调度单元参与电网的优化运行和安全供电。其中，基于需求响应的电力市场完全改变了家庭用户的传统用电模式和用电计划[1]。而家庭能量管理系统积极地响应了灵活电价机制，帮助用户管理家用电气设备，优化家庭负荷调度，实现用电经济、环保、舒适的目的。当电力用户的用电设备较多时，需要大量的采集装置，其安装不便且成本高。非侵入负荷监测NILM(Non-Intrusive Load Monitoring)在用户电力入口处对电流、功率等用电信息进行整体采集，可分析得到监测区域各用电设备的用电情况，简化了硬件结构与经济成本。采用非侵入式负荷监测技术，用户在电力供给的入口处安装监测设备就可以对家庭主要用电设备负荷进行监测，获得主要用电设备的负荷时序情况。

家庭能量管理系统依据家庭电气设备不同的工作特性，将其划分为温控型负荷设备、非温控型负荷设备和不可控制型负荷设备[2]，并且制定了相应的调度策略。常见的家庭温控负荷如电热水器、空调等，不仅日耗电量在家庭总耗电量中占比大，而且因为其特有的储热能力在响应动态变化的电价中具有很大的优化调度潜能。

家庭负荷的优化调度可视为一种利用时变电价进行最优化用户用电经济费用的决策优化问题。多种多样的家庭用电设备的用电特性设备模型已经得到了广泛研究，为智能用电运行优化方法奠定了数学基础[3-8]。在智能用电优化方法方面，国内外研究学者围绕用户经济性最优、用户舒适度最优、需求响应最佳、用电环保性最佳等多种优化目标研究了电气设备的优化调度。文献[3]在考虑用户舒适度的基础上建立了一个家庭温控负荷的热力学模型，并提出了两步循环调度策略。文献[4]进一步将家庭温控负荷的优化调度问题总结为混合整数非线性规划问题。不同于一般的求解方法，文献[5]针对家庭温控负荷决策优化问题采用了一种二叉树剪枝的新遍历算法，该算法可以使家庭温控负荷很好地参与电价响应和负荷调控。文献[6]针对家庭各个电气设备提出了负荷优先级的概念，并设计了基于负荷优先级的电气设备运行优化流程。文献[7]在文献[6]的基础上进一步提出了动态优先级的概念，并按照优先级顺序执行负荷控制决策。然而，以上研究都是在确定性环境中进行的，即认为家庭能量管理系统中的各种用户用电环境参数与用户用电行为参数均是恒定不变的，其值等于日前的预测值，这种假设在实际情况中是不合理的。这些输入参数的不确定性可能使日前生成的调度计划失去最优性甚至是破坏其可行性。

因此，考虑不确定参数的家庭用电设备的优化调度方法受到了国内外研究学者的广泛关注。文献[8]提出了基于智能电网环境的空调系统多目标优化算法，算法采用了情景消减技术和蒙特卡洛技术处理环境温度的不确定性。文献[9]针对空调设备将预测的实时电价与预测的室外环境温度不确定参数数学化为模糊集合，运用帕累托最优法求解以电费最低和室温违背最小为目标函数的模糊规划问题。文献[10-11]则在家庭能量管理系统中引入了模型预测控制技术，将模型的预测决策和实时调整相结合，有效地降低了电价预测与环境参数不确定性的影响。然而，模糊集合不仅需要大量的历史数据支持，隶属度函数的计算复杂度往往也超出了家庭能量管理系统的能力。模型预测控制技术则需要小步长地循环重复优化过程，增加了整个家庭负荷优化调度的计算时间。

针对不确定环境下的家庭温控负荷优化调度问题，本文以非侵入负荷监测数据为基础，以电热水器作为研究对象，引入机会约束规划模型解决约束条件中含有的随机变量问题。本文建立的随机变量及机会约束规划模型在描述不确定参数及其优化调度问题上具有简单、无需大量历史数据、计算负担小等优势。考虑到随机变量的概率分布，本文在不确定环境下结合随机模拟与粒子群优化PSO(Particle Swarm Optimization)算法进行优化调度求解，并通过设置不同的置信水平以反映随机变量对约束条件的影响机制。本文设置的置信水平可以很好地刻画用户对舒适度的容忍度。同时时变温度范围限制也被纳入了机会约束规划，从而可以求解得到不同用户模式下的调度策略。仿真结果表明，本文所提机会约束模型能够很好地应对家庭负荷优化调度的不确定性。

1 家庭温控负荷优化调度模型

1.1 电热水器的热力学模型

电热水器是家庭温控负荷的典型代表，其优化调度问题建立在电热水器运行特性的基础上。图1为在没有用户用水的情况下电热水器的热力学温度特性曲线。

图1 电热水器热力学温度特性曲线Fig.1 Thermodynamic temperature characteristic curve of electric water heater

传统的电热水器工作模式是：当热水器水箱中的水温不大于设置温度下限时，电热水器处于加热状态，热水温度上升；当热水器水箱中的水温不小于设置温度上限时，电热水器处于关闭状态，此时由于存在与环境介质热交换产生的热损失，热水温度下降。热水温度下降的另外一个重要原因是用户在使用热水的过程中电热水器有不断的冷水补充。电热水器的热力学动态过程可用以下公式描述[3]。

若电热水器在时段[ti,ti+1]内处于加热状态，则ti+1时刻热水温度θi+1为：

θi+1=θen,i+QR-(θen,i+QR-θi)e-Δt/(RC)

(1)

反之，若电热水器在时段[ti,ti+1]内处于关闭状态，则有：

θi+1=θen,i-(θen,i-θi)e-Δt/(RC)

(2)

若在时段[ti,ti+1]内有热水消耗，则该时段内的水箱将补充对应量的冷水，水温公式应该修正为：

θi=[θcur,i(M-di)+θen,idi]/M

(3)

其中，θen,i为ti时刻的外界环境温度；Δt=ti+1-ti为计算的时间步长；Q为电热水器在额定功率加热状态下的等效热力学参数；R为电热水器的热阻；C为电热水器的热容；di为时段[ti,ti+1]内用户的热水使用量；M为电热水器水箱的总容量；θcur,i为ti时刻电热水器在热水使用之前的热水温度。

式(1)—(3)共同描述了电热水器中热水温度的动态过程。文献[3]将涉及的电热水器热力学参数、热水需求量、环境温度和电热水器开关状态的动态过程归纳为一个统一表达式，如式(4)所示。

θi+1=f(θi,Δt,Q,R,C,di,xi,θen,i)

(4)

其中，xi为时段[ti,ti+1]内电热水器的状态，为1表示工作，为0表示不工作。

在统一表达式中，电热水器热力学参数一般可以认为是恒定不变的，其值可以从生产厂家获取或者通过拟合观测电热水器的性能曲线得到。

1.2 电热水器的优化调度模型

家庭温控负荷的优化调度在数学本质上是一个以用户电费最低为目标函数并且带有舒适度约束的数学规划问题。以电热水器为例，该调度模型的决策变量是未来24 h电热水器的工作状态，舒适度约束条件即为热水温度范围限制约束。电热水器的优化调度模型可以表示为[4]：

(5)

2 基于机会约束规划的不确定环境下家庭温控负荷优化调度

2.1 基于机会约束规划的温控负荷优化调度模型

在电热水器的优化调度模型中，不确定环境下的随机变量主要为预测的室外温度和用户用水量。这些变量的不确定性可能使日前生成的调度计划失去最优性，甚至出现违反运行或舒适约束的情况，因此必须在调度模型中对其进行考虑和处理。同时值得指出的是，这些变量的波动程度及对调度结果的影响因具体的用电环境和用户习惯而异，本文一般性地考虑这些不确定性同时存在时电热水器的优化调度问题。

日前预测的环境温度可以从气象部门的预报数据中获取，但是由于天气变化与预报准确度等因素的影响，其值并不是完全准确的，而是在一定范围内变化。用户使用热水的时间段和用水量均与用户的生活习惯息息相关，而且因为人行为习惯的主观性具有很大的随机性，其值也是在一定区间内波动。考虑这些主观性因素，同时参考文献[12]中算例关于不确定参数的均匀分布的假设，本文认为预测环境温度和热水用量均是均匀分布在一定区间范围内，即满足均匀分布的概率密度函数。

多个随机变量的存在导致原来的数学规划问题变为一种不确定规划问题。作为一种常用的处理不确定规划的方法，机会约束规划CCP(Chance Cons-traint Programming)由Charnes和Cooper提出，用于解决含多种不确定因素的复杂实际环境下应急电源的优化调度问题[13]，主要是针对约束条件中含有的随机变量，考虑其不确定因素，允许所做的决策在一定程度上不满足约束条件。带有随机变量的机会约束规划模型表示如下：

(10)

其中，ξ为一个随机向量；pr{·}为事件{·}成立的概率；αj为事先给定的约束条件的置信水平。在机会约束条件中，决策向量x为可行解的条件是：当且仅当事件{gj(x,ξ)≤0,j=1,2,…,p}的概率值不小于αj。

在本文中，电热水器优化调度模型中具有的随机变量为日前预测的环境温度与用户热水用量，且只出现在约束条件中。因此，本文采用机会约束规划处理带有随机变量的电热水器优化调度模型，形式如下：

(11)

依据机会约束规划理论，上限置信水平α1和下限置信水平α2分别用来限定水温上限与下限机会约束条件的违背程度。从用户角度而言，置信水平α反映了用户对违反温度条件约束的容忍度，其体现了用户对舒适度的考虑。α=1表示用户对温度范围约束要求极其严格，无论随机变量怎样变化均不可以违反其约束条件；α=0表示用户对温度约束范围完全不在意，这种情况和无约束条件情况的相同。

考虑到优化调度模型存在大量的约束条件，为了统一目标函数与约束条件，本文在目标函数中加入罚函数来处理约束条件。本文设计的罚函数如下：

(12)

(13)

本文在设计罚函数时，认为不同置信水平下违反约束条件时罚函数的值均为1。这样设计的目的是单一通过上下限的置信水平值控制上下限违限产生的罚函数值，避免多重罚函数值的影响。通过上述罚函数的设计，带约束的电热水器优化调度问题转化为式(14)所示的无约束的电热水器优化问题。

(14)

其中，ρ为惩罚系数，其值一般很大。从数学本质上看，电热水器的优化调度问题最终被转化为一个易于求解的无约束的非线性整数规划问题。

2.2 优化模型求解

传统的处理机会约束规划的方法是将机会约束条件转化为各自的等价类，但其前提是随机变量比较少，概率分布函数及其逆函数易于求解。但在本文模型中，机会约束条件存在多个随机变量，且随机变量的关系复杂、相互耦合，难以求解得到含独立随机变量的等价函数。而随机模拟技术以概率论为基础，通过多次模拟实验近似得到机会条件的真实值。因此该方法可以用来处理一切复杂的、无法转化为等价条件的问题，在实际工程上具有良好的适应性，故本文采用随机模拟技术处理复杂的机会约束条件。粒子群优化算法具有算法简单、易于实现、无梯度信息、参数少等特点，在求解非线性整数规划问题中表现出良好的效果。所以本文将随机模拟技术嵌入粒子群优化算法中对优化调度模型进行求解。

2.2.1 粒子群优化算法

粒子群优化算法是一种基于模拟鸟类种群搜索的随机演化计算方法，具有良好的全局搜索能力，因此被本文选为优化求解电热水器优化调度模型的主算法。而涉及随机变量的复杂机会约束条件则采用随机模拟算法处理。标准粒子群优化算法的原理如下。

设d维空间中第i个粒子的位置和速度分别为Xi和Vi，第i个粒子的个体最优位置为Pi，所有粒子中的最优位置为Pg，则每个粒子分别通过式(15)、式(16)更新各自的速度和位置。

vi,j(k+1)=wvi,j(k)+c1r1[pi,j(k)-vi,j(k)]+

c2r2[pg,j(k)-vi,j(k)]

(15)

xi,j(k+1)=xi,j(k)+vi,j(k+1)

(16)

其中，w为惯性权重；c1和c2为正学习因子；r1和r2为0～1之间均匀分布的随机数；k为迭代次数。由于上述优化调度模型是一个0-1规划问题，因此采用二进制编码的离散粒子群优化算法进行求解更加适合。其粒子速度会被限制在[-Vmax,Vmax]范围之内，位置更新公式如下[14]：

(17)

(18)

其中，random为一个[0,1]区间内均匀分布的伪随机数。

2.2.2 求解算法流程

根据电热水器优化调度模型，本文将随机模拟技术嵌入粒子群优化算法中进行求解，优化算法流程如图2所示。

图2 基于随机模拟技术的粒子群优化算法流程图Fig.2 Flowchart of PSO algorithm based on stochastic simulation technique

步骤1：读入数据。首先读入不确定环境下预测环境温度和用户热水用量的上、下限范围，计算相应的概率分布函数。然后读入电热水器的热力学参数与粒子群优化算法的算法参数。用户还需根据自身习惯设置热水温度约束限制范围和约束条件的置信水平。

步骤2：随机初始化粒子种群中各粒子的位置和速度。

步骤3：利用随机模拟方法处理机会约束条件。首先，置N′=0；然后，依据随机变量概率分布函数Φ(ξ) 产生N1个独立的随机变量ξ1、ξ2、…、ξN1作为样本，将样本代入约束条件，如果满足约束条件，则N′=N′+1，如此重复N1次。依据大数定理，当N1的值足够大时，可将N′/N1的值视为机会约束条件的实际概率pr{gj(x,ξ)≤0,j=1,2,…,p}。进而计算得到约束条件的罚函数值，并将目标函数值与罚函数值之和作为每个粒子的适应度，将当前各粒子的位置存储在各粒子的Pi(k)中，将所有个体中适应度最优对应的个体位置存储于Pg(k)中。

步骤4：利用粒子群优化算法的迭代公式(15)—(18)更新粒子的速度与位置。

步骤5：利用随机模拟方法重新计算每个粒子的适应度。对于每个粒子，将其适应度与其经历过的最好位置所对应的适应度进行比较，若较好，则将其作为当前的最好位置；比较当前所有粒子Pi(k)所对应的适应度值和Pg(k)所对应的适应度值，更新Pg(k)值。

步骤6：若满足停止条件(通常为预设的运算精度或迭代次数)，则搜索停止，给出最好的粒子作为最优解；否则返回步骤4继续搜索。

3 算例仿真及分析

3.1 算例参数

实时电价可以有效地反映电力供应与需求之间的关系，已经越来越受到电力企业的重视。文献[15]针对家庭用户给出了一种实时电价的预测方法，其预测实时电价如附录中图A1所示。

参考文献[5，16]中的实际历史环境温度与热水用量，满足均匀分布的次日环境温度和热水用水量的区间分布分别见附录中图A2、图A3。

式(1)—(3)中电热水器热力学参数如下：热阻R=0.762 3 ℃/kW，热容C=431.7(kW·h)/℃；电热水器额定功率为4.5 kW，对应的等效热力学参数Q=150 kW；水箱总容量M=189.27 L；电热水器初始水温为60 ℃；对于式(5)中涉及的温度约束上、下限值，本文考虑恒定温度约束区间与时变温度约束区间2种情况，恒定温度约束区间为[50，70]℃。本文综合考虑惩罚系数对解的可行域与算法局部寻优的影响，设惩罚系数值为100。

基于随机模拟技术的粒子群优化算法的参数设置如下：随机模拟的试验次数为1 000次；粒子群优化算法的种群规模为100，进化代数为200，粒子速度范围为[-3，3]，正学习因子c1=1、c2=1，惯性权重w=1。由于启发式算法不可避免地有陷入局部最优解的缺陷，所以本文每次求解过程中重复粒子群优化算法3次，取适应度值最低的一次为最优解。

3.2 算例结果分析

3.2.1 不同置信水平下优化调度结果

传统的电热水器工作模式使真实热水器水温在不确定环境中的多种随机变量作用下产生较大的偏差，不再能满足用户的舒适度要求。通过对不确定环境下随机参数的大量随机模拟实验，可得图3所示的传统工作模式下电热水器实际水温曲线。

卡塔尔的北方气田是世界最大气田，目前该气田已经建成7000万吨/年的液化天然气产能规模，但也只开发了其储量规模的近1/3，未来开发产能扩建潜力巨大。不过，卡塔尔政府近年国有化意识抬头，对国际油气公司的排斥越来越强烈，除非拥有独特的天然气开发处理技术，否则在该地区取得项目的难度越来越大。

图3 传统工作模式下电热水器实际水温曲线Fig.3 Actual water temperature curve of electric water heater under traditional operating mode

可见，室外温度与热水用量的不确定扰动会使得实际热水温度出现很大的波动范围。其中多个时段的水温均已经违背了用户的舒适度约束要求，热水温度最低可至43 ℃，这明显是用户无法接受的。

为了完全消除随机变量带来的不确定影响，本文为用户提供零容忍度方案。零容忍度方案是指用户完全无法容忍不确定参数对上下限温度约束条件的破坏，即置信水平α1和α2均应置为1。此时热水舒适度最符合用户的要求，用户体验最舒适。图4为零容忍度方案下的实际水温曲线。

图4 零容忍度方案下实际水温曲线Fig.4 Actual water temperature curve under zero-tolerance scheme

对比图3、4的实际水温曲线可知，机会约束规划得到的调度方案具有良好的鲁棒性，其决策结果可以在环境温度与用水量随机变化时，使水温始终在用户定义的舒适区间内，有效避免了不确定参数的扰动对用户舒适度的破坏。

上述基于零容忍度(即α1、α2均为1)的情况是一种极端情况。由于环境温度和用水量是均匀分布的随机变量，用户完全可以给予温度约束条件一定的容忍度，以达到减少电费的目的。此时，用户可以通过设置置信水平来达到舒适度与电费之间的平衡。此时，不同置信水平下计算得到用户的用电费如表1所示。

表1 不同置信水平下的用电费Table 1 Electricity expenses under different confidence levels

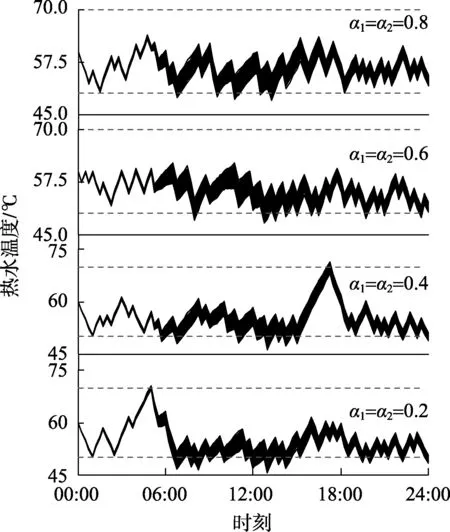
图5 不同置信水平下实际水温曲线Fig.5 Actual water temperature curve under different confidence levels

从表1中可以发现，零容忍度方案是用电费最高的一种方案，这是因为零容忍度方案具有最严格的约束要求，因此不可避免地导致了用户用电费的上升。随着置信水平的下降，用户对约束条件的容忍度变大，用户用电费也会不断地降低，这种经济性的获取是因为用户牺牲了舒适度造成的。用户可以依据容忍度设置不同的使用模式，例如，低容忍度则为舒适模式，高容忍度则为经济模式。当α分别为0.8、0.6、0.4、0.2时的实际水温曲线如图5所示。对比图4、5可以发现，实际水温曲线对约束条件的违背随着置信水平的降低而不断增大。特别需要指出的是，当置信水平为0时，用户完全不考虑约束条件，此时电热水器被安排全天关闭，用户用电费为0。

在以上的算例中，设置水温机会约束条件的置信水平上、下限取值相同，以分析置信水平与用户容忍度及经济性的关系。然而，相同的置信水平上、下限的条件下，实际的违背程度并不相同，从图5可以明显看出，下限的破坏程度要高于上限。模型是以最优化经济性作为目标，所以算法对水温下限机会约束的违背将高于上限。因此，本文新增一个对比算例，设置一种置信水平上限小于置信水平下限的情况(即设置α1=0.2，α2=0.8)，以反映差异化置信水平对用户上下限水温容忍度的不同影响。图6展示了差异化上下限置信水平下的实际水温曲线，从图中可看出水温上限违限程度要明显高于下限，说明置信水平上、下限将直接控制水温违限程度，置信水平较低的一方违限程度较大。因此只需通过差异化置信水平的取值就可以达到用户对于高水温的偏好需求。

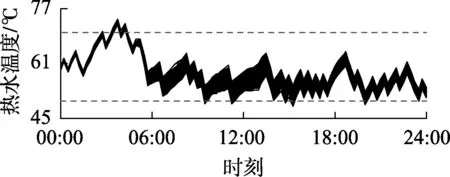
图6 差异化置信水平上、下限下的实际水温曲线Fig.6 Actual water temperature curve under confidence levels with different upper and lower limits

对比表1、2中的数据可以发现，时变温度约束区间下取相应的置信水平时，用户的用电费更低。这是因为时变温度约束区间允许调度方案产生更低的水温，节约了电费。与恒定温度约束区间下的结果一样，置信水平值越小，实际水温曲线对温度约束条件的违背越大。

表2 时变温度约束时不同置信水平下的用户电费值Table 2 Electricity expenses with different confidence levels under time-varying temperature constraints

图7 时变温度区间下实际水温曲线Fig.7 Actual water temperature curve under time-varying temperature constraints

4 结论

本文考虑了家庭温控负荷优化调度中多种随机变量的概率分布情况，建立机会约束规划模型，并结合随机模拟技术与粒子群优化算法对模型进行求解。本文首先给出零容忍度方案，仿真表明在随机变量的扰动下决策结果仍然可以满足用户舒适度要求，求解方案具有良好的鲁棒性，也证明了机会约束规划处理不确定环境下的家庭温控负荷调度问题的可行性与有效性。

本文设置不同置信水平以反映用户不同等级的容忍度，结果证明用户可以容忍损失一定舒适度来换取适当的经济性。而差异化的上下限置信水平的设置可以满足用户对高水温的需求。此外，本文在时变温度约束区间下进行了类似的仿真。时变温度约束区间的设置也使用户依据自身的温度喜好获取不同的用电决策结果。

附录见本刊网络版(http:∥www.epae.cn)。