计及控制设备动作次数约束的三阶段动态无功优化算法

覃 海，姬 源，周川梅，陈 胜，黄锦波，郑杰辉，李志刚

1. 贵州电网有限责任公司 电力调度控制中心，贵州 贵阳 550002；2. 华南理工大学 电力学院，广东 广州 510640)

0 引言

为了保证电网的安全、经济运行和优质供电，可以通过对有载调压变压器抽头、无功补偿装置和发电机无功出力的调度，达到提高电压质量和降低网损的目的，这是电力系统无功优化的意义[1- 6]。传统的静态无功优化是针对某个时刻的负荷，一般以有功损耗最小为目标并考虑电压等约束进行一个时间断面的无功优化。但是，由于一天24 h负荷是不断波动的，简单地进行静态无功优化将可能导致无功补偿设备和变压器抽头的频繁调整和投切，这会大幅缩短这些控制设备的使用寿命，在实际运行中是不允许这种情况出现的[7]。

因此，需要在无功优化模型中考虑控制设备动作次数约束，进行动态无功优化。动态无功优化问题是指在网络结构参数、未来一天各负荷母线的有功和无功变化曲线以及有功电源出力给定的情况下，通过调节发电机和无功补偿设备(主要是并联电容器组)的无功出力以及有载调压变压器的分接头，在满足各种物理和运行约束的条件下，使整个电网的全天电能损耗最小[8]。

在计及控制设备动作次数约束的动态无功优化中，除了各个时段的无功优化调度存在强耦合之外，变压器变比和电容器组的无功出力还是离散的，因此电力系统无功优化调度问题实际上是一个混合整数非线性规划MINLP(Mix-Integer Non-Linear Programming)优化问题。严格而言，这个问题属于一类非确定性多项式NP(Non-deterministic Polynomial)难问题[8-12]，其求解非常困难。虽然动态无功优化问题难以求解，但是针对单个时间断面进行的静态无功优化是无法满足实际运行需要的，所以必须进行动态无功优化，为网络运行方式的调整提供参考。

对于动态无功优化问题而言，快速地求出其全局最优解是非常困难的，目前已经有很多学者对这方面进行了研究。第一类方法是直接将控制设备全天动作次数的约束利用数学不等式表达，直接采用数学优化方法进行求解[13]。文献[14]通过对离散变量构造罚函数并将其嵌入非线性原对偶内点法中，以实现离散变量在优化过程中的逐次归整。第二类方法[15]是简化动态负荷，对日负荷曲线进行合理的分段，令负荷的分段数目等于控制设备动作次数的上限，然后对每个分段进行简单的静态无功优化，使动态优化的结果自动满足动态优化的约束条件。这类方法要求无功控制设备的动作具有同时性，即只能在负荷曲线分段处切换状态，而且需要人为分段时不便于运行人员进行使用。文献[16]则是依据有功网损曲线并人为给出分段数进行时间段的划分，然后对每个时间分段进行静态无功优化，从而将动态无功优化问题解耦成多个静态无功优化问题。而文献[17]认为，变压器可调抽头和无功补偿装置投切开关的允许操作次数表征的是设备的使用寿命，本质上是对经济性的考虑，所以将无功优化设备的动作次数约束转化为经济成本，构成目标函数的一部分，进而消除了每个时段之间的耦合约束。第三类方法是将动态无功优化问题分解成多个阶段进行求解。文献[18]提出了一种启发-校正两阶段动态无功优化算法，该方法没有考虑实际动态无功优化的最优解可能不需要无功控制设备按照其动作次数上限进行调节。文献[19]提出了动态无功优化模型的多阶段求解方法，将复杂的MINLP问题转化为非线性规划和混合整数规划2个子问题，分阶段进行求解。文献[20-21]利用二次锥规划方法将动态无功优化问题简化为凸的二次锥规划模型，从而大幅降低了求解的复杂度。此外，还有学者将调节效果最优、调节费用最低和调节设备最少[22]或调节设备动作次数最少[23]作为动态无功优化的目标函数，对其进行求解从而达到限制设备调节次数的效果。

综上所述，因为离散控制变量和连续控制变量共同存在，单个时段无功优化的求解也是相当复杂的，如果不考虑其中存在的离散变量问题，静态无功优化问题只是一般的非线性规划问题，可以用内点法进行求解。而相较于静态无功优化，动态无功优化还必须考虑控制设备动作次数约束，由于设备动作次数约束破坏了各个时段的独立性，使各个时段的无功调度和电压控制存在强耦合，令动态无功优化问题的求解非常困难。动态无功优化问题的复杂性和难度集中在如何高效处理离散变量和无功控制设备的动作次数约束2个方面，因此迫切需要提出一种快速、有效、实用的方法运用于工程实际中的动态无功优化问题。为此，本文借鉴文献[24]中考虑离散化发电调节约束的在线滚动调度的三阶段算法，并将此算法应用于求解动态无功优化问题，有效地处理离散控制变量和无功控制设备的动作次数约束等问题。

首先，给出静态的无功优化模型和考虑控制设备动作次数约束的动态无功优化模型；然后，详细介绍了三阶段动态无功优化算法，其核心是一种具有多项式计算复杂度的前推-回推式动态无功规划算法；最后，以IEEE 30节点系统和某实际区域电网为例，验证了本文所提算法的实用性和正确性。

1 计及控制设备动作次数约束的动态无功优化模型

1.1 静态无功优化模型

建立数学模型是处理优化问题的基础，对于每个单一的时段而言，可以认为其负荷保持不变，所以单一时段内的无功优化就相当于一般意义上的静态无功优化。选取发电机无功出力、无功补偿设备的无功补偿容量、有载调压变压器变比为无功控制手段，以节点电压和松弛节点的有功出力为状态变量，不等式约束包括发电机所发无功、电容器和电抗器无功补偿容量、变压器变比的上限和下限约束等，以此建立的静态无功优化模型具体如下，其中无功补偿容量和变压器变比都是离散变量。

假设系统有NB个节点、NT台有载调压变压器、NG台可调发电机，有NC个节点装设可投切电容器组，全天总时段数为T。静态无功优化模型如下：以系统全天有功网损最小为目标函数，如式(1)所示；式(2)和式(3)为功率平衡约束，式(4)和式(5)为状态变量的不等式约束，式(6)—(8)为控制变量的不等式约束。

(1)

Bijsinθij,t)=0i=1,2,…,NB

(2)

(3)

(4)

(5)

(6)

(7)

(8)

1.2 动态无功优化模型

(9)

(10)

式(9)和式(10)分别为电容器组和变压器分接头日调节最大次数约束，其中，uCc,t和uTi,t为0-1决策变量，分别描述第c台可投切电容器组和第i台有载调压变压器在时段t的动作状态，为1表示动作，为0表示未动作。

2 三阶段动态无功优化算法

严格而言，动态无功优化问题属于一类NP难问题，其求解非常困难。如何快速地求解动态无功优化问题，获得一个相对满意的次优解，在实际工程应用中则显得更有价值。为此，本文提出一种三阶段算法，将动态无功优化问题分解成3个阶段进行求解。下文将对该算法进行详细的说明。

2.1 阶段1：不考虑调节约束的静态无功优化

在阶段1不考虑可投切电容器组和有载调压变压器的调节次数约束，将可投切电容器组数、有载调压变压器分接头档位等离散变量松弛为连续变量，这样在此阶段的无功优化问题只是一个非线性规划问题，可借助一些成熟的算法进行求解，如内点法。

2.2 阶段2：阶段化理想曲线

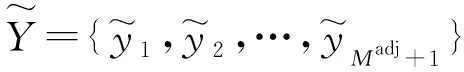
(11)

其中，y0为变量在初始时段(t=0)的值，为一个给定的数值；S为满足变量上下限约束的可行集合。

对于优化问题式(11)，可以采用一种前推-回推式动态规划算法进行求解。

假设阶梯曲线中某个分段的首、末端分别为a、b，定义该分段与理想曲线Y*对应子段的最小欧氏距离为：

(12)

可以得到：

(13)

(14)

式(12)—(14)在变量是连续的情况下才成立，如果考虑可投切电容器组数和有载调压变压器分接头档位是离散变量的情况，需要对上述公式进行修改。

确定指标体系的常用方法包括层次分析法、专家咨询法、主成分分析法、熵值法、非模糊数判定矩阵法、优序图法等[12]．选择熵值法作为本文指标体系权重的计算方法,其基本思路是通过计算指标的信息熵,根据指标的变化程度来决定指标权重．信息量越小,不确定性就越大,熵也就越大;信息量越大,不确定性就越小,熵也就越小[13]．

假设离散变量值为Δdisc的整数倍，那么有：

(15)

(16)

当第m个分段的首端点为im=k时，记第m—Madj个分段与理想曲线Y*的欧氏距离之和的最小值为f(m,k)，即：

(17)

根据贝尔曼最优性原理，有：

(18)

a. 对所有的0≤a≤b≤T，计算d(a,b)。

b. 令f(Madj,k)=d(k,T)(k=1,2,…,T)。

c. 令m=Madj-1。

d. 遍历k=0,1,…,T，计算式(19)。

(19)

e. 若m=1，执行步骤f；否则，令m=m-1，并执行步骤d。

f. 计算式(20)。

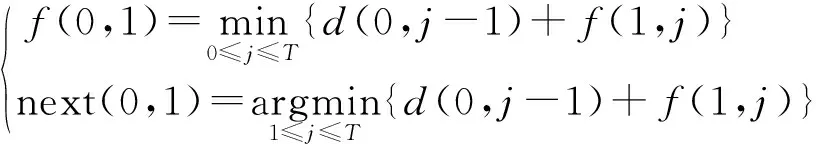
(20)

h. 遍历m=1,2,…,Madj，计算最优分段下第m个分段的最优出力，即：

(21)

上述算法中的步骤d—f属于回推过程，步骤g和h为前推过程。容易得知该算法的计算复杂度为O(MadjT2)，属于多项式复杂度算法。该算法的计算效率高且易于实现，能够快速地实现理想的可投切电容器组无功补偿容量曲线和理想的有载调压变压器变比曲线的阶梯化，具有工程实用性。

2.3 阶段3：分配失配功率

对理想的可投切电容器组无功补偿容量曲线和理想的有载调压变压器变比曲线进行阶梯化，会破坏原有的潮流约束，产生失配功率，所以，需要在已知的可投切电容器组无功补偿容量和有载调压变压器变比的情况下，求解式(22)所示优化模型，得到最终的发电机有功和无功出力值。

(22)

该优化模型是一个非线性规划模型，可以采用阶段1的求解方法进行求解。

本文所提三阶段算法的具体求解流程图如图1所示。

图1 求解动态无功优化的三阶段算法流程Fig.1 Flowchart of three-stage algorithm for solving dynamic reactive power optimization

3 算例分析

利用Visual C++ 9.0编程，在主频为3.1 GHz、内存为4 GB的计算机上对算例进行仿真验证。阶段1和阶段3的模型都是非线性规划模型，可以直接调用IPOPT求解器[25]进行求解。

3.1 IEEE 30节点系统算例

首先以IEEE 30节点测试系统为例，该系统有4条变压器支路、6台发电机和6个无功补偿节点，因此可以采用无功调节设备(投切电容器)、有载调压变压器和调节发电机无功出力3种方式实施无功调节，从而达到降低网损的目的。其中有载调压变压器和电容器的参数分别如表1和表2所示(表2中容量上、下限和分级步长均为标幺值)。

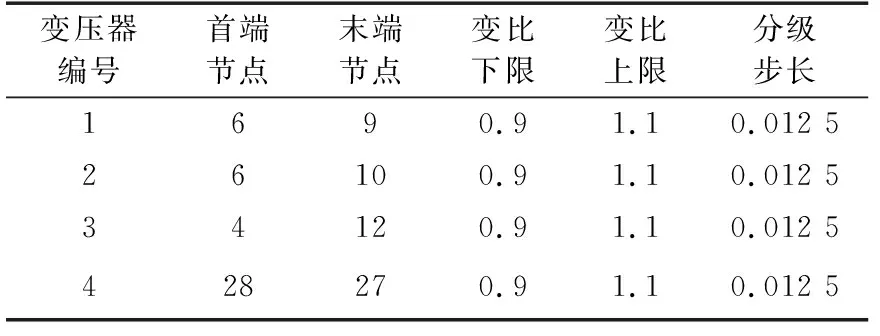
表1 IEEE 30节点系统中有载调压变压器参数Table 1 Parameters of on-load tap changing transformers in IEEE 30-bus system

表2 IEEE 30节点系统中电容器参数Table 2 Parameters of capacitors in IEEE 30-bus system

图2 典型日负荷曲线Fig.2 Typical daily load curve

首先，不考虑无功调节设备，只通过调节发电机无功出力和变压器变比(连续)，计算24个时段的无功优化，系统总的网损为33.54 MW，共耗时2.8 s，结果如表3所示。

表3 不同情景下无功优化结果对比Table 3 Comparison of reactive power optimization results under different scenes

采用本文所提方法，首先在阶段1将离散变量松弛为连续变量，不考虑无功调节设备和变压器分接头调节次数限制，进行24个时段的静态无功优化，得到系统总的网损为28.27 MW，计算时间为2.9 s。在阶段1得到的理想的变压器变比曲线和理想的无功调节设备无功补偿容量曲线分别如图3、图4所示。然后在阶段2进行阶梯化理想曲线。规定无功调节设备和变压器分接头每天的最大调节次数为4次，假设在00∶00时刻，变压器的初始变比值为1，无功调节设备的初始无功补偿容量为0。可以得到离散化后的变压器分接头调节和无功调节设备投切结果，分别如图3、图4所示。固定离散变量的结果后，将其代入动态无功优化模型，进行阶段3的求解，重新校正连续变量(发电机有功和无功出力)的优化量。得到最终发电机无功出力如图5所示。阶段3的动态无功优化计算耗时5.0 s，最终的网损为28.94 MW，而实际的最优值应该介于28.27～28.94 MW，因此，本文所提三阶段算法的最大误差率为2.3%。

3.2 某实际区域电网算例

在本节利用本文所提三阶段动态无功优化算法对某实际区域电网进行仿真验证，其中某实际区域电网的参数如表4所示，发电机总容量为23 647 MW，某时刻总负荷为21 704 MW。该系统典型日的负荷曲线(标幺值)如图6所示。

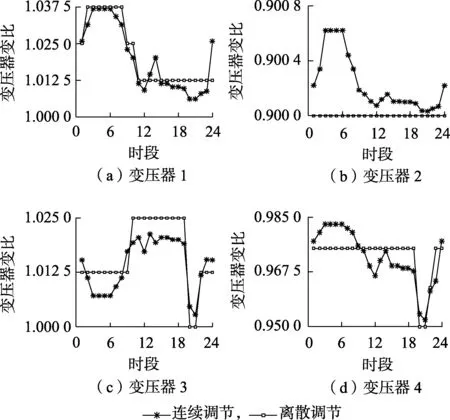
图3 变压器变比的离散化结果Fig.3 Discretization result of ratios of transformers

图4 无功补偿量的离散化结果Fig.4 Discretization result of reactive power compensation capacity

图5 发电机的无功出力Fig.5 Reactive power output of generators

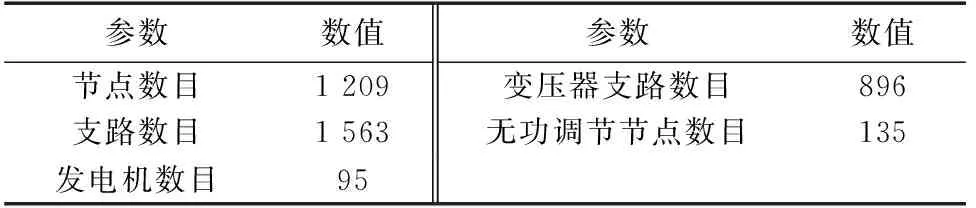
参数数值参数数值节点数目1 209变压器支路数目896支路数目1 563无功调节节点数目135发电机数目95

图6 实际系统日负荷曲线Fig.6 Daily load curve of an actual power grid

综合考虑系统运行的安全性与经济性的要求，将无功调节设备和变压器分接头每天的最大调节次数设为8次。利用本文所提算法计算一天24个时段的动态无功优化，结果如表5所示。可以看出，考虑无功调节设备的无功补偿时，系统有功网损更小。

由表5可以看出，对于实际系统而言，本文所提三阶段动态无功优化算法可以在满足控制设备动作次数约束的情况下，快速地求解无功优化问题。结果显示，某实际区域电网的动态无功优化结果与实际精确解之间的最大误差为5.7%，验证了本文所提算法的正确性和适用性。

表5 某实际区域电网在不同情景下无功优化结果对比Table 5 Comparison of reactive power optimization results under different scenes for an actual regional power grid

4 结论

为了高效地求解动态无功优化这一大规模、多时段、强耦合的非线性混合整数规划问题，本文提出了三阶段动态无功优化求解方法，将计及控制设备动作次数约束的动态无功优化问题的求解分解为多个时间断面的连续无功优化计算、理想的无功调节设备无功补偿容量曲线和变压器变比曲线的阶梯化以及在确定各个时段的无功补偿容量和变压器变比情况下的连续无功优化计算3个阶段。对IEEE 30节点系统和某实际区域电网进行测试分析，测试算例结果表明，本文所提算法能够在短时间内获得满足控制设备动作次数约束的次优解，验证了所提算法具备计算速度快、处理约束有效、优化效果好的特点，具有工程实用性。