基于WNN-GNN-SVM组合算法的变压器油色谱时间序列预测模型

张施令,姚 强

国网重庆市电力公司电力科学研究院，重庆 401123)

0 引言

电力变压器是电力系统中的重要设备，其运行状态直接关系到电网的安全稳定运行，而电力变压器本体内部油中溶解气体的体积分数及其变化规律与变压器的故障模式关系密切，因此油中溶解气体分析DGA(Dissolved Gas Analysis)技术的应用较为广泛[1-5]。而电力变压器油中溶解气体体积分数随时间的变化关系实际上为多维时间序列，该序列以相同时间间隔或不同时间间隔排列，包含了电力变压器所处外界环境、运行状况与油中溶解气体体积分数的内在关系，因此可通过该时间序列的预测揭示电力变压器的运行状况，并以此为基础对电力变压器故障类型进行判定[6]。

文献[7]将一种新的贝叶斯组合神经网络模型应用于短期交通流量的预测，其中贝叶斯组合神经网络由反向传播神经网络和径向基函数(RBF)神经网络构成，该组合模型具有较高预测精度且预测稳定。文献[8]将阶梯遗传算法和BP神经网络联合应用于铁路客运量时间序列预测，预测效果优于单一BP神经网络预测模型。文献[9]提出利用思维进化算法优化BP神经网络、粒子群优化(PSO)算法优化支持向量机(SVM)和基于单隐层前馈网络极限学习机组合进行预测的综合预测体系，其用于微电网的短期负荷预测时具有较高预测精度。以上研究表明时间序列预测应用较为广泛，依据已获取历史时间序列进行数值拟合并在一定时间域内进行预测具有较大实际应用价值。

目前较多文献均应用单一时间序列预测方法，例如BP神经网络和径向基神经网络等[10-11]，这些单一预测方法通过对网络权值与阈值进行修正可得到具有一定精度的预测效果。为进一步提高预测精度，学者提出了组合预测模型，即将各种单一预测模型按照一定规则进行组合[12-13]，综合利用单一预测模型的优势达到提高预测精度的目的。

另一方面，电力变压器是电力系统中最重要的设备之一，若电力变压器发生故障，则可能引起电网大停电。为及时发现电力变压器故障，国际电工委员会推荐将DGA作为油浸式变压器故障诊断方法。目前已有文献将DGA数据与BP神经网络、粗糙集技术以及SVM等结合对变压器故障进行有效诊断[14-16]。本文将小波神经网络(WNN)、灰色神经网络(GNN)和SVM进行结合，并通过粒子群优化算法优化BP神经网络(PSO-BP)算法对以上WNN、GNN、SVM进行优化，对电力变压器DGA历史时间序列进行短期预测。

本文首先介绍了WNN、GNN、SVM的原理，分别选取了其拓扑结构优化变量，并利用PSO算法对这3种单一预测方法进行结构参数优化，提出了基于PSO-BP算法的时间序列组合预测模型，并推导得出了组合预测模型最优权系数的计算方法。本文研究结果对于电力变压器DGA数据预测，并以此为基础对电力变压器故障类型进行判定均具有一定的指导意义。

1 单一时间序列预测方法理论分析

1.1 基于WNN的时间序列预测

小波函数由1个母小波函数经过平移与尺寸伸缩得到，小波分析即把信号分解为一系列小波函数的叠加。小波变换是指把某一基本小波函数φ(t)平移τ后，再在不同尺度γ下与待分析的信号x(t)做内积：

(1)

对式(1)进行等效拉普拉斯变换得：

(2)

WNN是在BP神经网络基础上以小波基函数作为隐含层传递函数，其拓扑结构如图1所示。图1中，X1、X2、…、XM为WNN的输入；Y1、Y2、…、YN为WNN的输出；ωij和ωjl为WNN权值，i=1，2，…，M，j=1，2，…，J(J为小波基函数数量)，l=1，2，…，N。当输入向量[X1，X2，…，XM]输入小波基函数时，其中一小波基函数的输出可表示为：

(3)

其中，h(j)为隐含层第j个节点输出值；γj、τj分别为第j个小波基函数的尺度和平移。

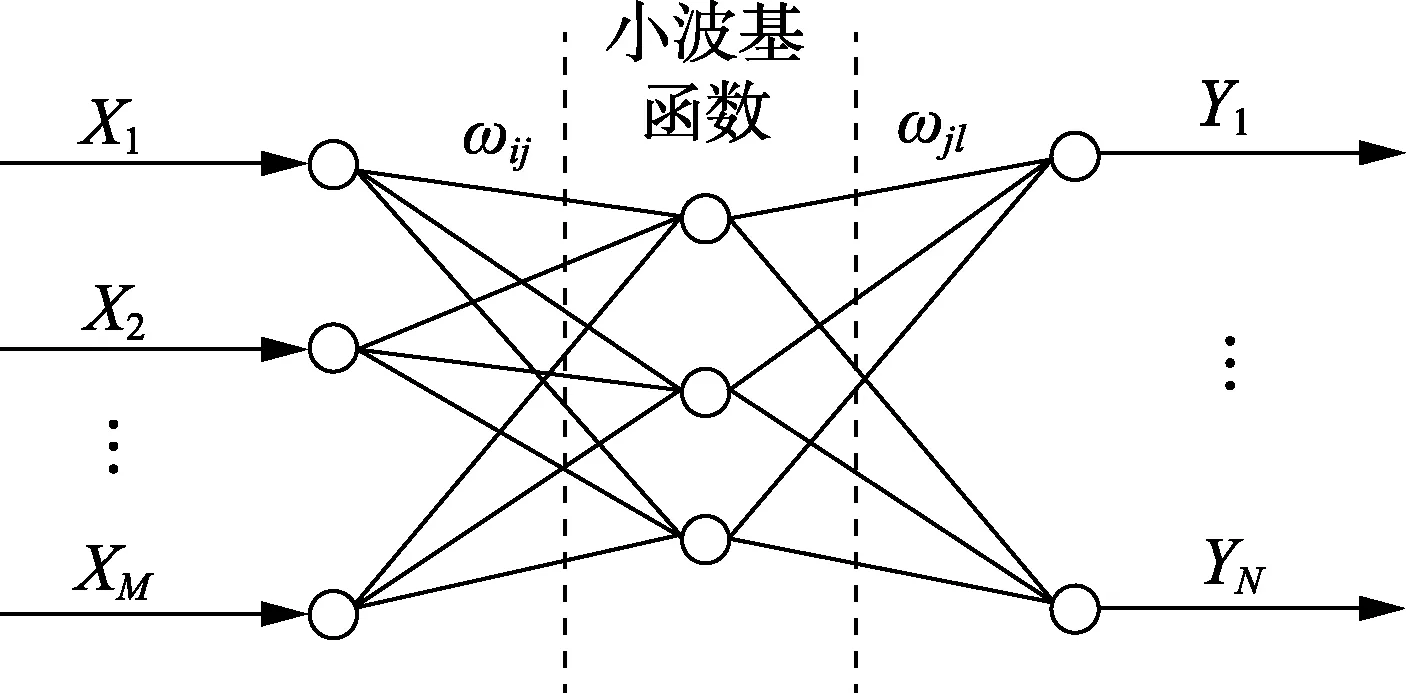
图1 WNN拓扑结构Fig.1 Topology of WNN

1.2 基于GNN的时间序列预测

(4)

其中，y2、…、yn为GNN的输入参数；y1为GNN输出；a1、b1、b2、…、bn-1为微分方程的系数。令b1y2+b2y3+…+bn-1yn=u，则式(4)的通解为：

(5)

其中，k为待定常数。

将式(5)映射到BP神经网络中即为n输入、1输出的GNN，其拓扑结构如图2所示。图中，t为输入参数序号；GNN分为A、B、C、D 4层，网络权值为：ω11=a1，ω21=-y1(0)，ω2i=2bi-1/a1(i=2，3，…，n)，ω3i=1+e-a1t(i=2，3，…，n)。

图2 GNN拓扑结构Fig.2 Topology of GNN

1.3 基于SVM的时间序列预测

SVM与BP神经网络拓扑结构类似，SVM中间节点的线性组合构成输出，其中每个支持向量与中间节点对应，结构如图3所示。SVM用于回归拟合预测的基本思想是寻求一个最优分类面，目标是使训练样本距最优分类面误差最小。设有L个训练样本{(xi，yi)}，其中i=1，2，…，L;yi为对应的输出值。建立线性回归函数如式(6)所示。

f(x)=wΦ(x)+b

(6)

图3 SVM拓扑结构Fig.3 Topology of SVM

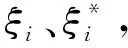
引入Largrange函数，并转换为对偶形式后可得回归函数为：

(7)

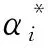
(8)

因此SVM主要涉及的参数包括权重系数C和核函数参数g。

2 WNN-GNN-SVM组合算法的实现

单纯基于一种方法进行时间序列预测具有片面性和不稳定性，假设历史时间序列x1、x2、…、xn，WNN、GNN、SVM对该历史时间序列的预测值为xi1、xi2、…、xin(i取1、2、3时分别对应WNN、GNN、SVM的预测值)，预测误差矩阵E为[1]：

E=[(eit)3×n][(eit)3×n]Ti=1，2，3

(9)

其中，i取1、2、3时分别对应WNN、GNN、SVM；eit=P(t)-Pi(t)，为第t时刻的预测误差，Pi(t)为预测时间序列。传统组合预测模型为：

P′(t)=w1P1(t)+w2P2(t)+w3P3(t)

(10)

其中，w1+w2+w3=1。令W=[w1w2w3]为预测模型线性组合的加权系数。线性组合预测误差平方和为：

(11)

为求得组合预测模型的最优权系数W，可将上式转换为二次规划问题：

(12)

继续引入Largrange算子2λ(RTW-1)，分别对W和λ求导得：

W=λE-1R

(13)

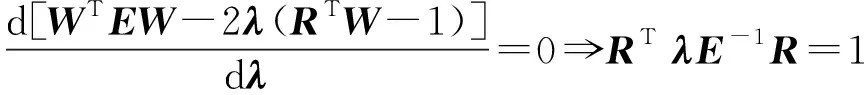
λ=(RTE-1R)-1

(14)

因此最优权系数W=E-1R/(RTE-1R)。

在此基础上，提出一种基于BP神经网络的时间序列组合预测模型，可有效利用各种预测方法的优势，提高时间序列预测的精度和可靠性。组合模型的基本建模思路为：

a. 利用WNN、GNN、SVM分别对时间序列进行预测，并通过PSO算法优化其拓扑结构优化变量；

b. 基于以上3种单一模型的预测结果，结合最优权系数计算方法，获得权系数组合模型预测结果；

c. 将预测得到的4组灰色预测结果作为BP神经网络的输入向量，以原始历史时间序列作为BP神经网络输出向量，建立基于BP神经网络的组合模型并应用PSO算法进行优化，其拓扑结构如图4所示。

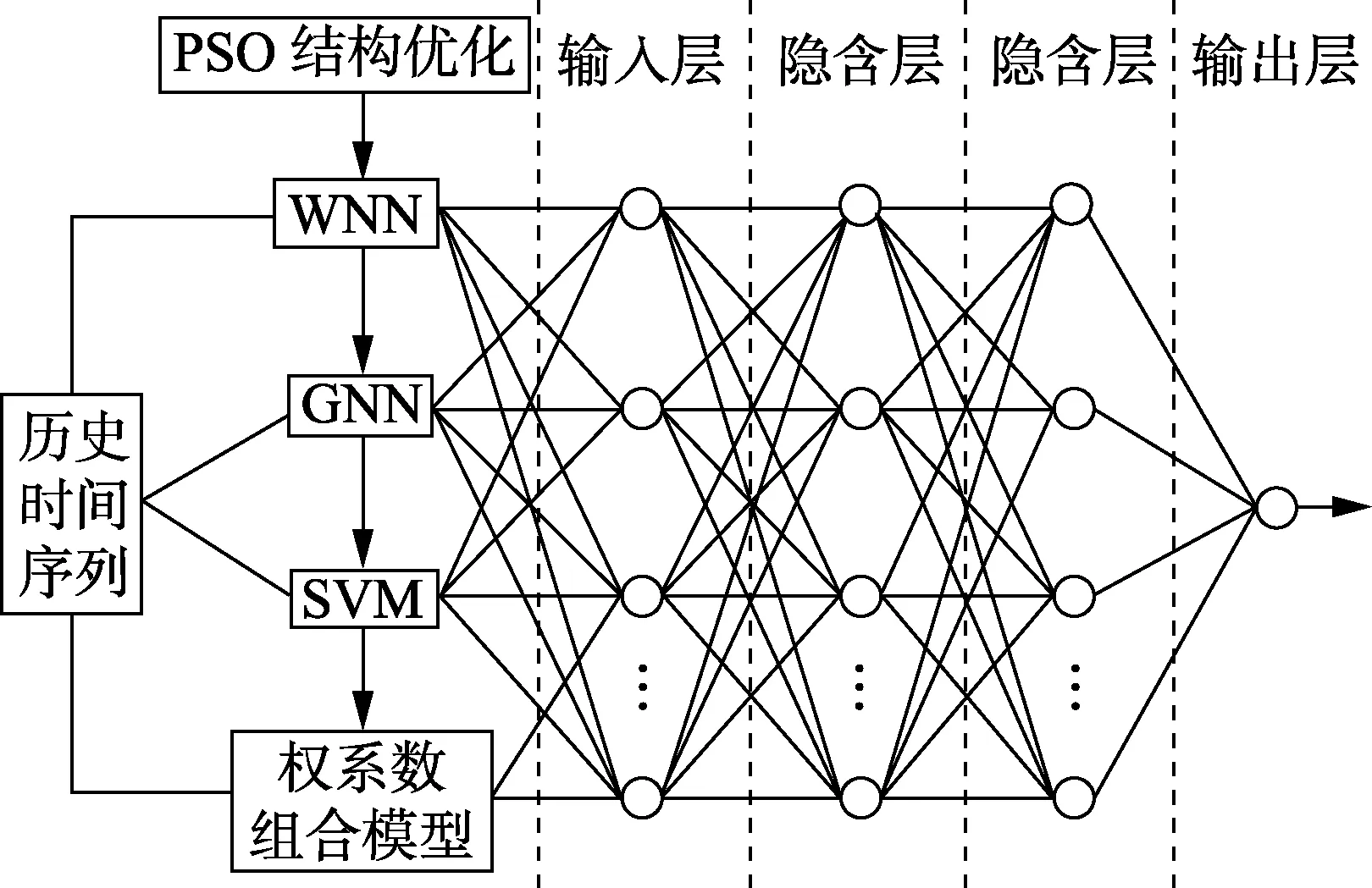
图4 基于PSO-BP算法的时间序列组合预测模型Fig.4 Combined forecasting model of time series based on PSO-BP algorithm

3 预测实例计算与分析

3.1 原始数据的选取与预处理

变压器油在过热或者放电故障条件下将分解生成特征气体，气体主要包括氢气(H2)、二氧化碳(CO2)、甲烷(CH4)、乙烷(C2H6)、乙烯(C2H4)、乙炔(C2H2)6种故障气体，气体含量及比例对于故障类型的判断具有参考价值[17-19]。对某变压器进行周期性变压器DGA时，发现其总烃超过了注意值，随后进行了跟踪试验，发现各种气体的体积分数均快速升高，以氢气、甲烷2种气体的体积分数为例验证本文所提组合预测方法的准确性。

WNN、GNN和SVM的输出向量为氢气或甲烷的含量，输入向量为除输入向量外另外5种气体的含量。组合预测模型期望达到的目标是输入已知的5种气体含量，输出目标是对应时间点处氢气或甲烷的含量。文中仿真建模平台为MATLAB(R2009b)，运行环境为Intel Core i5-3230，4 G内存，500 G硬盘，通过MATLAB自带函数mapminmax，结合apply和reverse命令满足WNN、GNN和SVM的输入需要[20-21]。

3.1.1 SVM预测模型

采用高斯径向基核函数作为SVM核函数，涉及的优化参数包括权重系数C和核函数参数g，基于交叉验证原理，通过PSO算法对SVM模型进行参数寻优，提高SVM模型的预测效果[22]。PSO算法参数设置：学习因子c1=1.5、c2=1.7，算法进化代数为300，粒子种群的最大数量为20。SVM的权重系数C∈[0.1,100]，核函数参数g∈[0.01，1 000],SVM Cross Validation参数的初始值设定为3。对氢气体积分数的时间序列进行预测时，SVM的最佳参数设置为C=5.66、g=0.25；对甲烷体积分数的时间序列进行预测时，SVM的最佳参数设置为C=1.41、g=0.18。

PSO算法对SVM的优化效果见图5，SVM对氢气、甲烷体积分数的时间序列预测结果见图6。

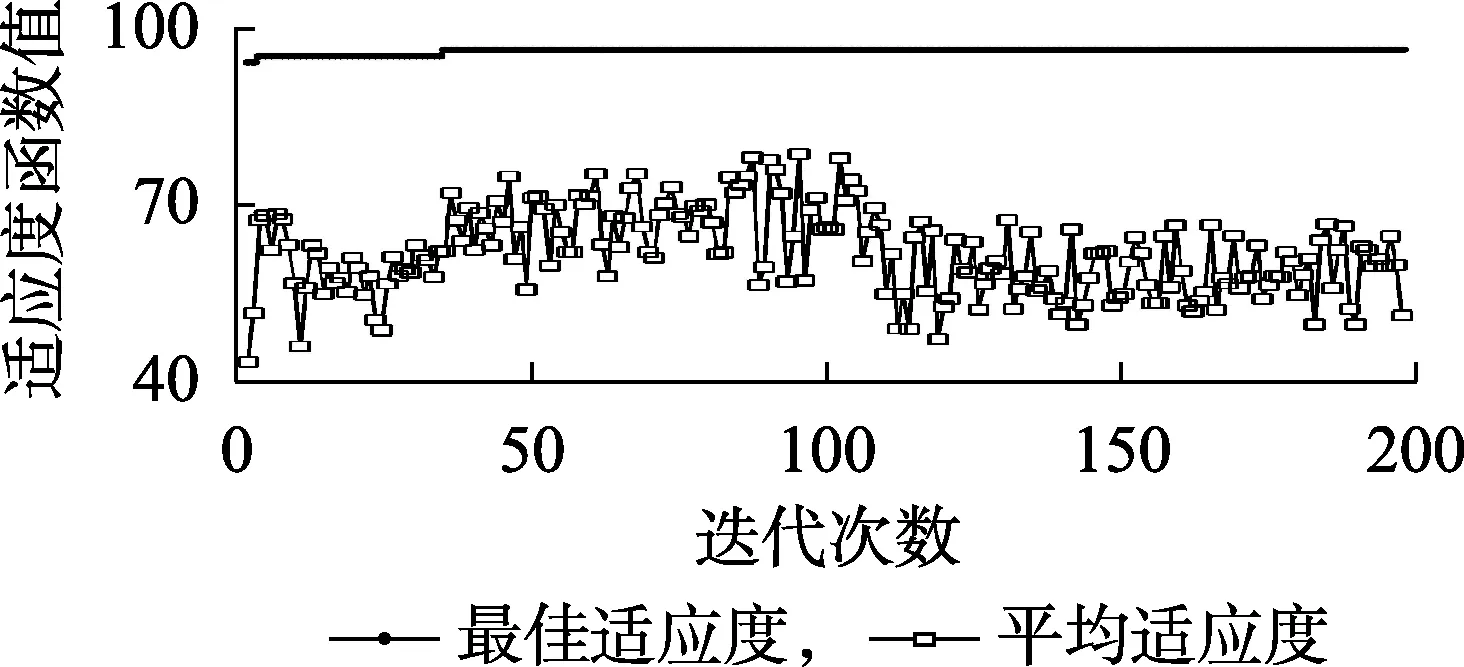
图5 PSO算法优化SVM效果Fig.5 Optimizing effect of PSO algorithm on SVM

图6 SVM对氢气和甲烷的时间序列预测结果Fig.6 Prediction results of time series of H2and CH4 volume fractions by SVM

3.1.2 WNN预测模型

WNN参数设置为：5个输入节点和1个输出节点，10个隐含层节点；参数学习率为0.01，学习迭代次数为200次；网络神经元间权值初始值应用randn函数随机赋值；在学习过程中采用Morlet母小波基函数。应用PSO算法对WNN进行网络权值和神经元阈值的优化过程中，PSO算法的参数设定与SVM一致，WNN在对氢气、甲烷体积分数时间序列预测误差变化趋势如图7所示。由图7可见，在PSO算法优化WNN的过程中，随着迭代次数的增加，适应度函数值在前几次迭代过程中收敛较快，然后趋于平稳，这表明PSO算法对WNN的权值、神经元阈值的优化过程逐渐趋于收敛，优化效果良好。

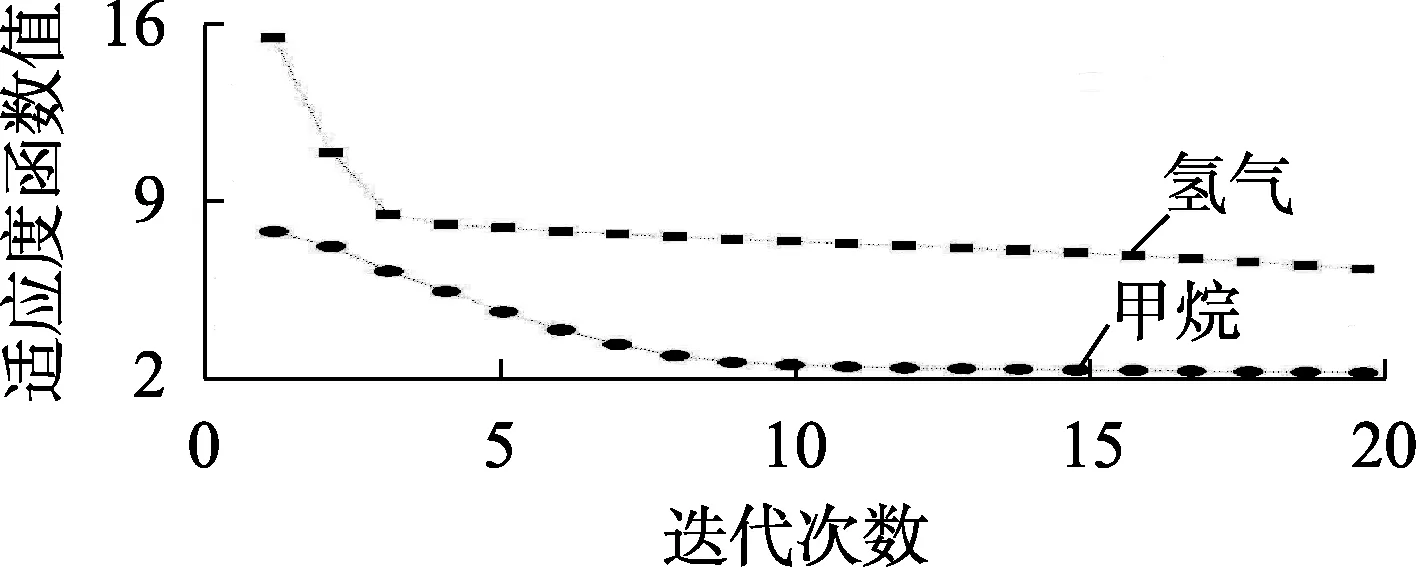
图7 WNN预测误差收敛情况Fig.7 Prediction error convergence of WNN

WNN对氢气、甲烷体积分数时间序列的预测结果如图8所示。由图可见，经过PSO算法优化后，WNN的预测结果更加接近时间序列真实值，且前15个时间序列点预测精度较高，然后预测序列逐渐发散，精度降低趋势。

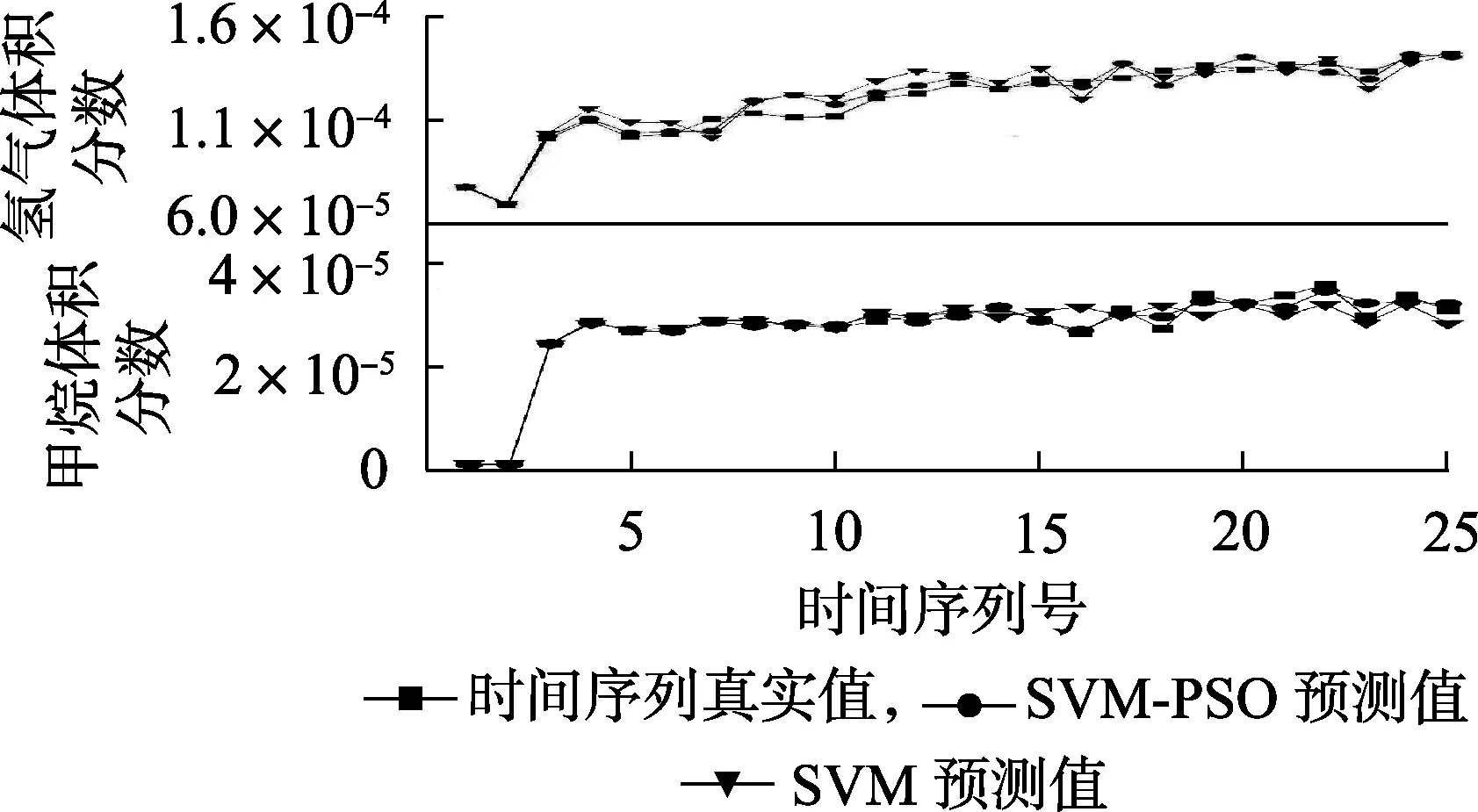
图8 WNN对氢气和甲烷体积分数时间序列的预测结果Fig.8 Prediction results of time series of H2and CH4 volume fractions by WNN

3.1.3 WNN预测模型

GNN需对网络初始化参数a、bn-1进行初始化，通过rand函数随机赋值，其中灰色神经网络的优化参数包括a1、b1、b2、b3、b4、b5、b6，在优化过程中PSO算法的参数设定与4.1.2节中一致。GNN模型首先对特征气体体积分数的原始时间序列进行一次累加，累加后的时间序列呈现准指数变化规律，然后通过一阶微分方程对其进行拟合。经过PSO算法优化后的GNN预测模型适应度函数值随迭代次数的变化如图9所示。由图可见，适应度函数值逐渐减小而趋于稳定，证明了PSO算法优化GNN的稳定性。

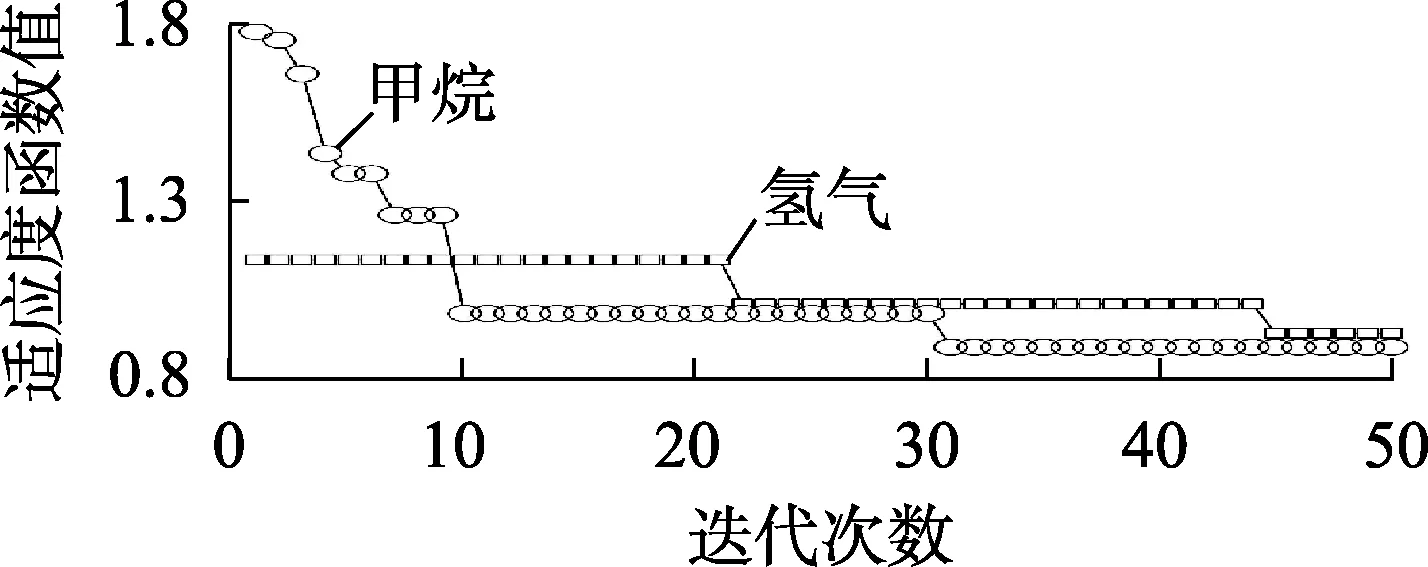
图9 适应度函数值随迭代次数变化关系Fig.9 Relationship between fitness function and iteration number

GNN对氢气、甲烷体积分数时间序列的预测结果如图10所示，由图可见经过PSO算法优化后，GNN的预测精度提高，但GNN对前10个时间序列点的预测精度较低，出现了预测时间序列点跳变的情况。

图10 GNN对氢气、甲烷体积分数时间序列的预测结果Fig.10 Prediction results of time series of H2 and CH4 volume fractions by GNN

3.2 组合模型修正预测时间序列

限于篇幅，后文以甲烷体积分数时间序列为例对组合预测模型进行讨论。依据SVM-PSO预测模型、WNN-PSO预测模型、GNN-PSO预测模型的预测值与真实时间序列得到预测误差矩阵e[1，3]，限于篇幅略去矩阵中部分元素。

(24)

相应的预测误差矩阵E为：

E=[(eit)3×n][(eit)3×n]T=

(25)

将预测误差矩阵E代入W=E-1R/(RTE-1R)中得到组合预测模型的最优权系数W：

(26)

因此传统组合预测模型为：

P′(t)=0.832 8P1(t)+ 0.186 5P2(t)-0.019 3P3(t)

(27)

将传统组合预测模型预测结果与真实时间序列进行对比，结果如图11所示。

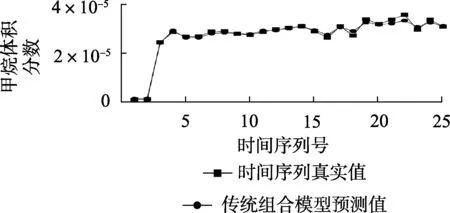
图11 传统组合预测模型预测结果Fig.11 Prediction result of traditional combination model

图11表明应用权系数修正的传统组合预测模型可将甲烷体积分数的时间序列预测精度进一步提升，前15个时间序列点的预测值基本和时间序列真实值一致，在后10个时间点处出现了预测偏差。

3.3 基于PSO-BP算法的组合预测模型

文中提出的组合预测模型基于SVM-PSO、WNN-PSO、GNN-PSO和传统组合预测模型的预测结果，因此将BP神经网络的输入层设置为4个，输出层设置为1个，用于组合预测模型输出的时间序列；中间层神经元个数设定为6个；PSO算法用于优化BP神经网络的权值和神经元阈值。BP神经网络组合预测模型的预测结果如图12所示。

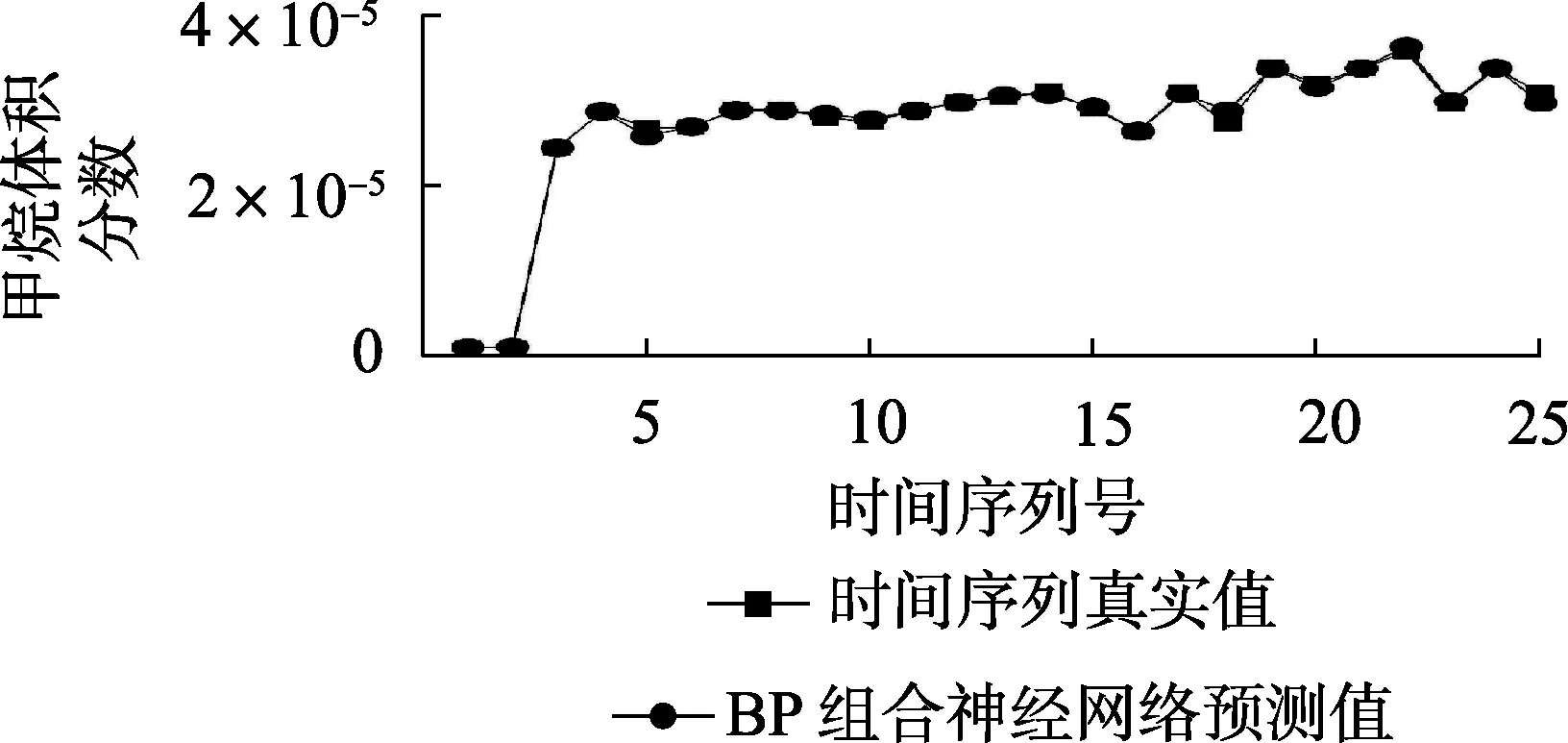
图12 PSO-BP组合预测模型预测效果Fig.12 Prediction result of PSO-BP combination model

图12表明BP神经网络组合预测模型的预测值与时间序列真实值基本吻合，经过PSO算法优化后，BP神经网络组合预测模型表现出较强的非线形拟合能力和预测性能。

4 讨论

利用SVM、WNN、GNN、SVM-PSO、WNN-PSO、GNN-PSO、传统组合模型、基于PSO-BP算法的组合预测模型对甲烷体积分数进行预测，根据甲烷体积分数时间序列真实值与预测值分别计算绝对平均误差E1、均方根误差E2、最大绝对误差E3和序列相关度系数E44个指标来评定各个预测模型的预测精度，如图13所示。图中，预测算法序号1— 8分别对应SVM、PSO-SVM、WNN、PSO-WNN、GNN、PSO-GNN预测模型、传统组合模型、基于PSO-BP算法的组合预测模型。

图13 预测模型预测效果对比Fig.13 Comparison among predicting models

图13表明SVM、WNN、GNN经过PSO算法优化后，平均误差E1、均方根误差E2、最大绝对误差E3均显著降低，序列相关度系数E4增大，这说明时间序列预测精确度提高。传统组合模型和基于PSO-BP算法的组合预测模型的4个评价指标均优于其他6种预测模型，表明了组合预测模型的优势，且基于PSO-BP算法的组合预测模型的E1、E2、E3更低，具有更好的预测精度。

5 结论

本文分析了WNN、GNN、SVM的原理，并应用PSO算法对上述3种基本预测方法进行结构参数优化，提出了基于PSO-BP算法的组合预测模型，PSO算法通过优化WNN、GNN、SVM预测模型的拓扑结构参数可提高其预测精度，将WNN、GNN、SVM预测模型与PSO-BP算法进行组合，并应用PSO算法优化组合预测模型的拓扑结构参数，组合模型较单一模型有更高的预测精度。本文提出的预测方法适用于变压器油色谱的时间序列预测，也可用于电力系统其他时间序列的预测。