自适应陷波理论及其在轴承故障诊断中的应用

万书亭，张 雄，庞 彬，豆龙江

华北电力大学 机械工程系，河北 保定 071003)

0 引言

滚动轴承是机械设备中应用最广泛的零部件之一，其运行状况影响着整个系统的工作状态，滚动轴承的故障识别与诊断对于保证机械设备的安全可靠运行具有重要意义。实际工况下，滚动轴承受运行状态及工作环境影响，其故障冲击信号常常与多种噪源干扰融合，且存在转频调制现象。从调制信号中将故障冲击信号解调出来一直是机械故障领域的难点问题。近年来，故障冲击特征提取方法被广泛研究，从传统的递归式经验模态分解(EMD)，到局部均值分解，再到变分模态分解(VMD)，以及各类分解方法的改进形式[1-5]，信号的分解能力及自适应性逐渐增强，对冲击成分的提取愈加有效。Antoni等系统地定义了谱峭度，先后提出了基于短时傅里叶变换的谱峭度法及谱峭度图的快速算法，并将其应用到旋转机械的监测和故障诊断中。最大相关峭度解卷积[6-10]是一种可以在低信噪比的情况下，通过提升信号峭度值达到降噪目的，从而提取微弱冲击成分的方法。无论是滤波方法、信号分解方法还是解卷积方法，其对信号共振频带的依赖均很大，且其通过抑制噪声干扰增强冲击特征，并未针对性地对工频干扰采取措施，而实际工况中故障冲击特征往往被工频干扰所淹没。

陷波具有快速滤除工频载波信息的能力，与其他滤波器不同，陷波的参数设计取决于工频转速信息，而不依赖于共振频带。但是由于陷波具有窄带滤波特性，其对中心频率及带宽参数变化较为敏感。而人工参数选择的主观性较大，且多参数选取工作量大。因此，本文提出一种粒子群参数优化方案以有效地解决陷波过程中中心频率及带宽的参数选择问题。

1 基本理论

1.1 自适应陷波器

1.1.1 陷波原理

在信号分析中，信号会被工频干扰所淹没，通过窄带滤波可以将这些工频干扰滤除。陷波的目的就是通过构成窄带滤波消除单个的正弦干扰信号，且其他频率成分都能通过。

对于二阶数字陷波，假设要滤除的频率为ω0，滤波器的幅度特性在ω=ω0处为0，在其他频率上接近常数。零点z=e±jω0使陷波器的幅度特性在ω=±ω0处为0。为使离开零点后，幅度迅速上升到某个常数，将2个极点放在非常靠近零点的地方，极点为z=re±jω0，传递函数为：

(1)

其中，r为半径，与陷波器的带宽有关，0≤r≤1；b0为增益系数。设陷波器在 -3 dB处的频带带宽定义为Bw，则Bw和增益系数b0为：

(2)

当使用归一化频率时，Bw=1-r。不同的r和带宽Bw，对应不同的 -3 dB处的频带和陷波器深度，如图1所示。

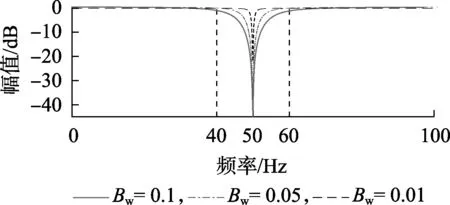
图1 陷波器幅值响应Fig.1 Amplitude response of trap filter

当r较小而Bw较大时，ω=±ω0附近的频率分量会受到显著的影响；而当r→1时，陷波器带宽Bw减小，同时陷波深度也减小。所以设计陷波器时需要根据实际要求选择r值。

1.1.2 粒子群优化陷波器参数

粒子群优化算法[11]具有良好的全局寻优能力，因此采用粒子群优化算法实现陷波中心频率及带宽这2个参数的自适应选取。假设D维空间中，种群X=(X1，X2，…，XM)包含M个粒子，其中第i个粒子Xi=(xi1，xi2，…，xiD)表示1个D维向量，代表第i个粒子在D维搜索空间中的位置。第i个粒子的速度为Vi=(vi1，vi2，…，viD)，Pi=(pi1，pi2，…，piD)为个体局部均值，G=(g1，g2，…，gD)为种群全局极值，各粒子通过Pi和G迭代更新自身速度和位置：

(3)

其中，ω为惯性权重；d=1，2，…，D；i=1，2，…，M；α为当前迭代次数；c1和c2为加速度因子；η为[0，1]范围内的随机数。

利用粒子群优化算法寻优时，需要确定一个适应度函数，粒子每次更新位置时需要计算当前位置对应的函数值，通过对比进行更新。信号中冲击成分的比重影响峭度指标的大小，信号包含的冲击成分越多[12]，峭度值越大，因此本文将进行陷波处理后信号的峭度值K作为适应度函数，表达式如下：

(4)

其中，x为振动信号；μ为信号x的均值；E(·)表示取均值运算；δ为信号x的标准差。

利用粒子群参数寻优的具体步骤如下：

a. 初始化粒子群优化算法的各项参数，参数值如表1所示；

b. 初始化粒子种群，以参数组合[ω0，Bw]作为粒子的位置，随机初始化各粒子的位置与移动速度；

c. 计算每个粒子的位置对应的适应度值;

d. 对比适应度值的大小并更新种群全局极值；

e. 更新粒子的位置和速度；

f. 循环迭代，转至步骤c，直至迭代次数达到最大设定值，输出最佳适应度值及粒子的位置。

表1 粒子群优化算法各项参数Table 1 Parameters of particle swarm optimization algorithm

1.2 自适应陷波流程图

自适应陷波流程图如图2所示。

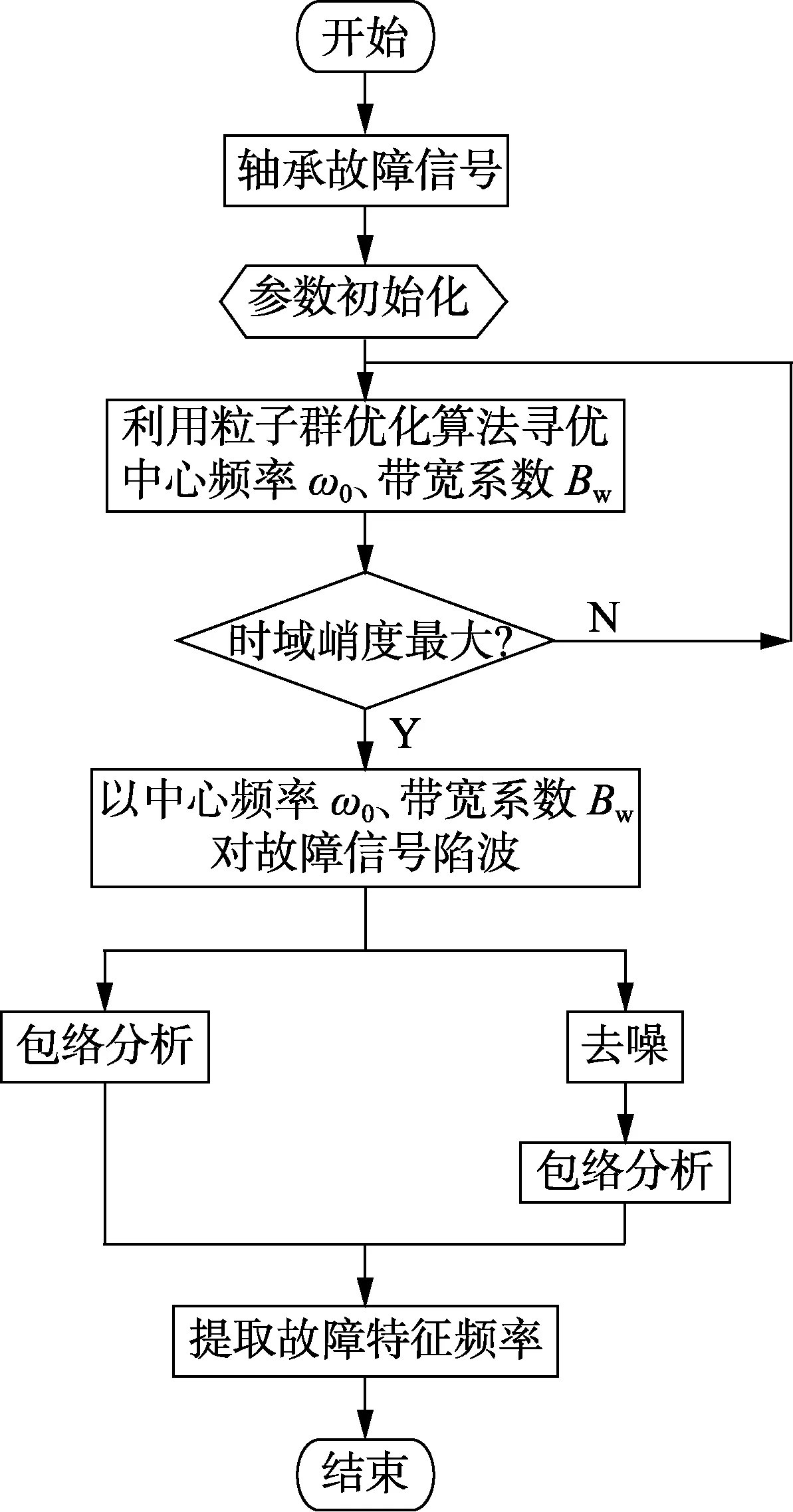
图2 自适应陷波流程图Fig.2 Flowchart of adaptive trap

2 仿真信号分析

为验证自适应陷波方法能够有效从调制信号中滤除工频干扰，还原故障冲击特征，采用文献[13]中的滚动轴承内圈故障模型进行分析，数学模型如式(5)所示。

(5)

其中，τi为第i次冲击相对于平均周期T的微小波动；Ai为以1/fr为周期的幅值调制，fr为轴承所在工作轴的转频，fr=20 Hz；CA=0；A0=2；h(t)为指数衰减脉冲；B为系统的衰减系数；内圈故障通过频率为130 Hz；fn=3 kHz为系统固有频率；φA、φω为初相位。设置采样频率fs=8 192 Hz，取8 192点数据分析。冲击信号的时域波形如图3所示。

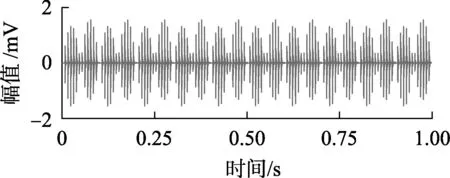
图3 冲击信号时域波形Fig.3 Time-domain waveform of impulse signal

在原始故障仿真模型中混入fc=20 Hz的工频载波信号C(t)=5 sin(2πfct)，调制信号的时域波形如图4所示，信号中原有的冲击特征被工频载波信号淹没。

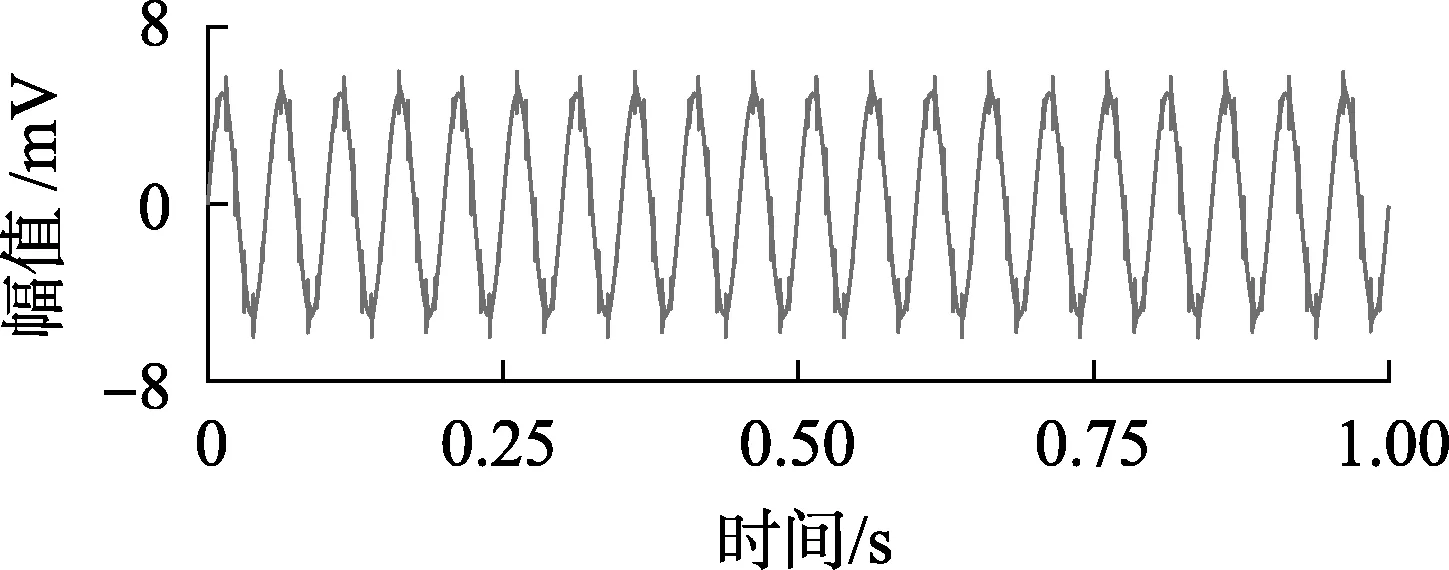
图4 调制信号时域波形Fig.4 Time-domain waveform of modulating signal

陷波器的参数设计取决于工频转速信息，而不依赖于共振频带，但是陷波器具有窄带滤波特性，所以对中心频率及带宽参数的变化较为敏感。考虑到人工参数选择的主观性较大，且多参数选取工作量大，本文提出自适应陷波方法，利用粒子群多参数寻优能力，根据最大峭度准则自适应选取陷波参数。

初始化参数，设定中心频率搜索范围为[19，21] Hz，带宽系数搜索范围为[0，1]。图5为峭度值随进化代数变化的曲线，峭度值8.66出现在第15代进化种群中，此时陷波中心频率ω0=20 Hz、带宽Bw=0.2。所设计的陷波器幅值响应曲线如图6所示，工频陷波后，其波形如图7所示，从图7中可以看出，调制信号的工频信息被滤除，冲击特性被有效解调出来。

图5 峭度值随进化代数变化的曲线Fig.5 Value of kurtosis varying with evolutionary algebra

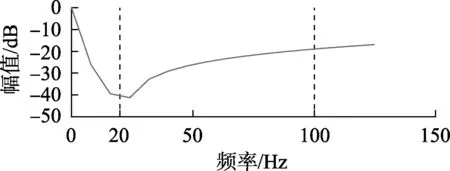
图6 陷波器幅值响应图Fig.6 Amplitude response of trap filter

图7 工频陷波后的时域波形Fig.7 Time-domain waveform of power frequency trap

为验证粒子群优化参数选择的合理性，将中心频率及带宽修改为[20 Hz，0.1]、[20 Hz，0.6]、[21 Hz，0.2]3种组合，在3种组合参数下陷波的时域波形见图8。对比图3、图7、图8可看出：图8(a)陷波后波形边界翘曲严重；图8(b)陷波过度，冲击能量衰减；图8(c)中心线波动，存在微弱正弦工频影响。

图8 不同陷波参数下的时域波形Fig.8 Time-domain waveforms of different trap parameters

进一步验证，以波形匹配方差S2为评价指标表征不同参数下陷波后的冲击特征与原始信号的匹配程度，波形匹配方差数值越小则波形匹配程度越高，其结果见表2。

(6)

其中，yi为陷波后信号序列；xi为原信号序列；n为采样点数。

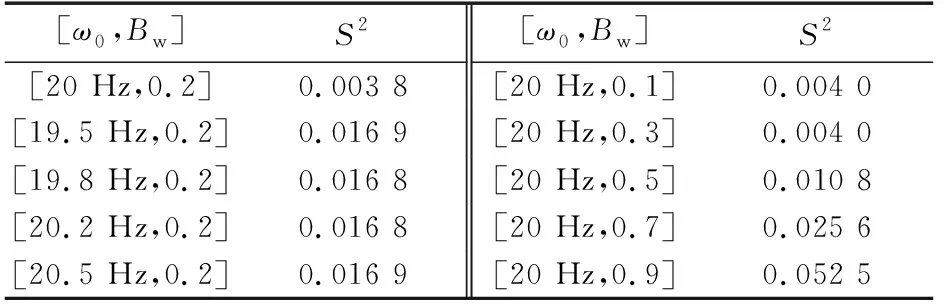
表2 不同参数陷波后的波形匹配方差Table 2 Values of S2 under different trap parameters

3 实验信号分析验证

3.1 微弱故障实验分析

为了验证本文方法对轴承轻微故障诊断的有效性，采用美国Case Western Reserve大学的滚动轴承数据，轴承型号JEMSKF6023-2RS。故障源是滚动体表面通过电火花加工的直径分别为0.177 8 mm、0.355 6 mm、0.533 4 mm的凹坑。选用最轻微的0.177 8 mm故障数据进行分析，采样频率为12 kHz，轴的转速为1 730 r/min。滚动轴承参数尺寸如表3所示，滚动轴承发生外圈故障、内圈故障和滚动体故障时的故障特征频率分别为88、143、115 Hz。

表3 滚动轴承参数Table 3 Parameters of rolling bearing

取8 192点数据进行分析，图9为滚动轴承故障信号的时域波形，直接对其进行包络分析，结果如图10所示。由图10可见，包络谱中成分复杂，滚动轴承的滚动体微弱故障信息被噪声频率淹没。

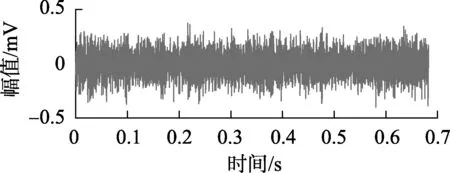
图9 滚动轴承故障信号时域波形Fig.9 Time-domain waveform of rolling bearing’s fault signal

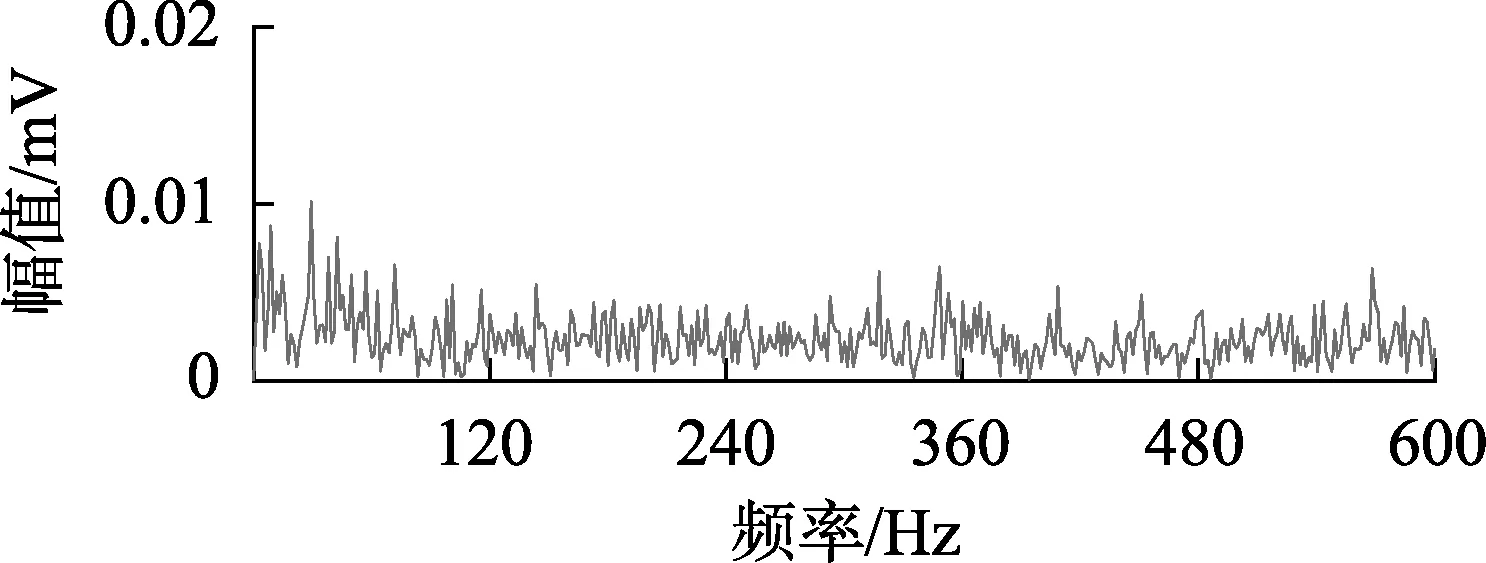
图10 滚动轴承故障信号包络谱Fig.10 Spectrum envelope of rolling bearing’s fault signal

利用粒子群多参数寻优特性设计自适应陷波器，初始化参数，根据轴转速(1 730 r/min)设置中心频率搜索范围为[26，30]Hz、带宽范围为[0，1]，根据最大峭度准则确定陷波中心频率及带宽。图11为峭度值随进化代数变化的曲线，最大峭度出现在第16代进化种群中，此时陷波中心频率ω0=29.3 Hz(此时实验转频为28.8Hz，考虑为实验转速设置误差引起)，带宽Bw=0.6。所设计的陷波器幅值响应曲线如图12所示。工频陷波后，其波形如图13所示，从图中可以看出，调制信号工频信息被滤除，冲击特性被解调出来。参数选择不当(ω0=28 Hz，Bw=0.1)时的陷波后信号的包络谱如图14所示。对比图13、14可知，当参数选择不当时，陷波未得到理想效果。

图11 峭度值随进化代数变化的关系曲线Fig.11 Value of kurtosis varying with evolutionary algebra

图12 陷波器幅值响应图Fig.12 Amplitude response of trap filter

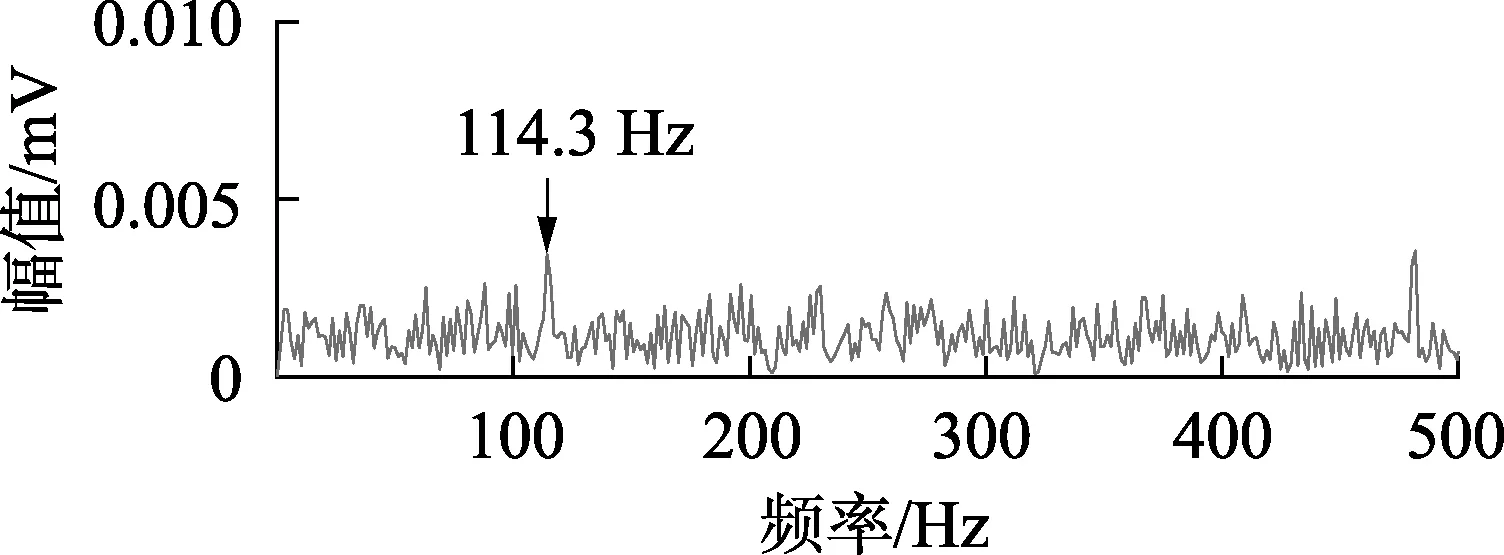
图13 陷波后信号的包络谱(ω0=26 Hz，Bw=0.2)Fig.13 Spectrum envelope of signal after trap，when ω0=26 Hz and Bw=0.2

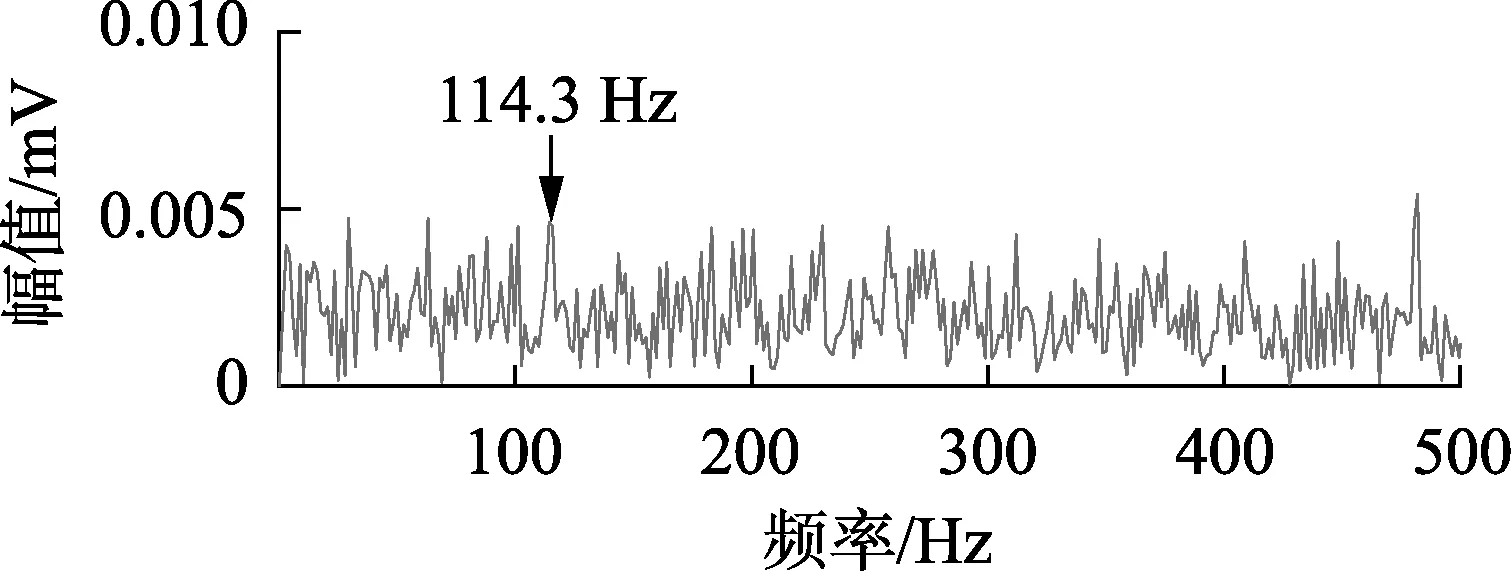
图14 陷波后信号的包络谱(ω0=28 Hz，Bw=0.1)Fig.14 Spectrum envelope of signal after trap，when ω0=28 Hz and Bw=0.1

以陷波作为前置工频降噪处理方法，结合集合经验模态分解(EEMD)及VMD方法对滚动轴承故障信号进行分析。

EEMD算法是Wu[14]等在EMD算法的基础上，利用高斯白噪声频率均匀分布统计特性，在原信号中混入适当标准差和叠加次数的高斯白噪声，以消除原信号间断现象的一种自适应分解方法；VMD[15]方法可以将1个信号分解成为预定个数的准正交子模态，每个模态分量具有频率中心和有限带宽，将信号分解问题转换到变分模型中进行分解，在各分量之和等于原始输入信号的约束下，寻求各分量的聚集带宽之和最小，其实质是多个自适应维纳滤波器组，具有类似于小波包的频率分割特性。

对原始信号进行EEMD，通过相关系数准则[16]选取最大的2组本征模态函数(IMF)分量进行信号重构，对重构信号进行包络谱分析，结果如图15(a)所示。从图15(a)中可以看出，滚动轴承故障特征频率115.7 Hz被提取出来，但其谱线并不突出，相较于图13所示的陷波处理结果，其干扰谱线较多，且倍频成分仍未能准确提取到。进而对原始信号进行工频陷波，对陷波后信号进行EEMD后重构降噪，结果如图15(b)所示。从图15(b)中可以看出，故障特征谱线较突出，干扰谱线得到有效抑制，且能寻找到2倍频(230 Hz)。

图15 滚动轴承故障信号的EEMD和陷波-EEMD包络谱Fig.15 Spectrum envelopes of rolling bearling’s fault signal after EEMD and EEMD-trap

同理，以陷波为原始前置处理，以VMD后重构为后置降噪处理(VMD的分解个数K采用中心频率相离准则[17]选取，惩罚因子默认为2 000)，VMD信号包络谱及陷波-VMD包络谱如图16所示，可见陷波对于增强冲击特征有一定的意义。

图16 滚动轴承故障信号的VMD和陷波-VMD包络谱Fig.16 Spectrum envelopes of rolling bearing’s fault signal after VMD and VMD-trap

3.2 复合故障试验分析

为了进一步验证自适应陷波方法对轴承故障特征频率信息提取的有效性，在QPZZ轴承故障模拟试验台上完成了滚动轴承故障模拟实验，试验平台的结构见附录中的图A1。试验采用6205E轴承，使用线切割机在滚动轴承内圈上加工出深1.5 mm、宽0.2 mm的凹槽模拟轴承外圈、内圈故障，如附录中的图A2所示。采用数据采集卡由安装在轴承座上的加速度传感器采集振动信号，采样频率为12 800 Hz，电机转速为1 468 r/min，滚动轴承参数尺寸如表4所示。

表4 滚动轴承参数Table 4 Parameters of rolling bearing

轴承内圈故障特征频率fi、外圈故障特征频率fo分别为：

(7)

其中，Z为滚动体个数；D为节圆直径；d为滚珠直径；α为接触角；N为电机转速。

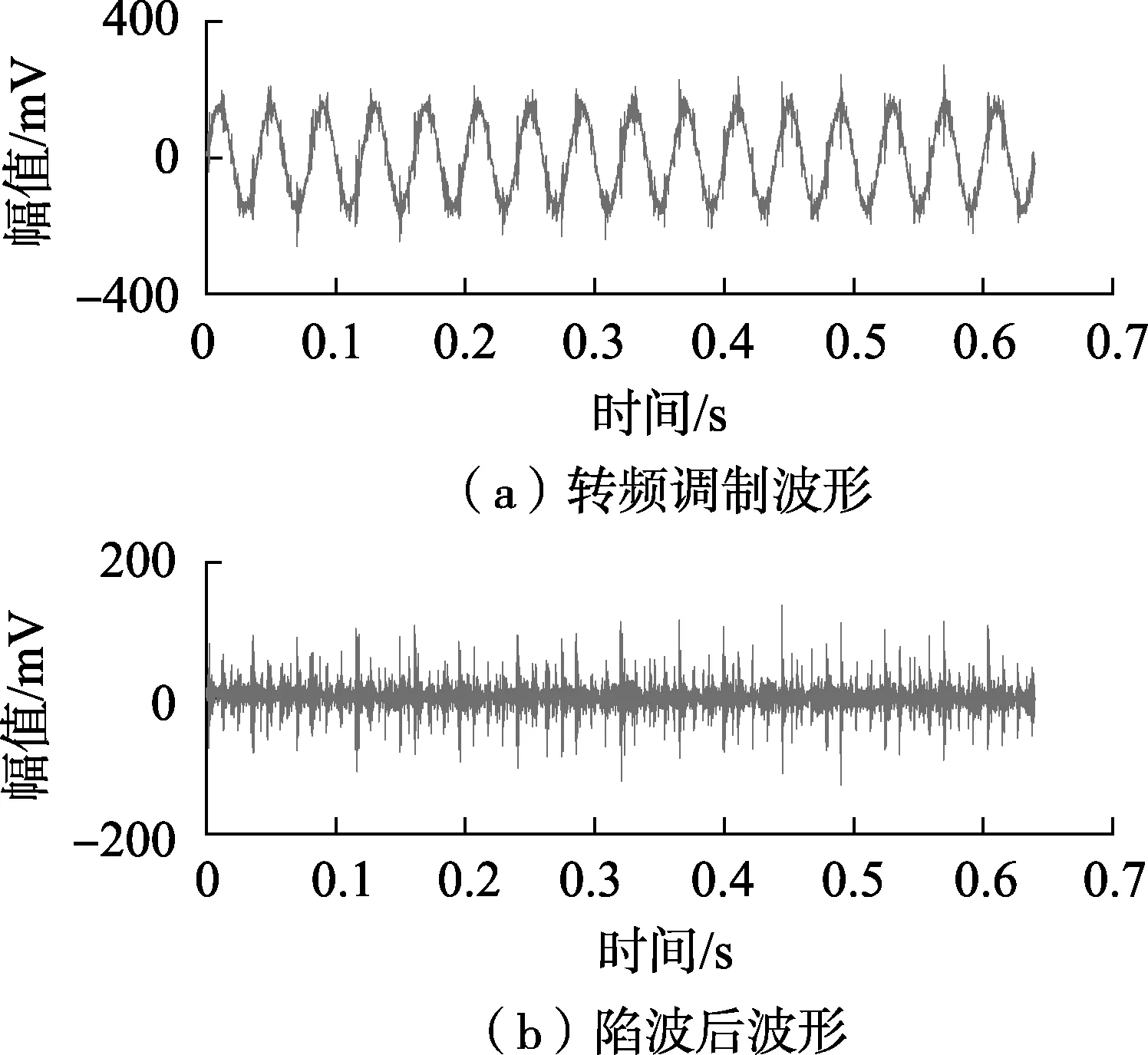
图17 时域波形Fig.17 Time-domain waveforms

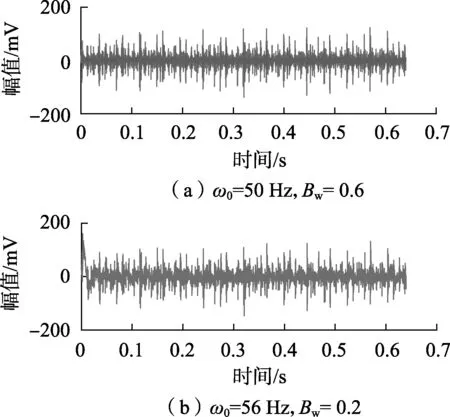
图18 不同陷波参数下的时域波形Fig.18 Time-domain waveforms under different trap parameters

对时域信号进行采集，取8 192点数据分析，未处理前的转频调制波形及自适应陷波(ω0=50 Hz，Bw=0.2)后的冲击特征时域波形如图17所示，由图可见，自适应陷波方法可以将正弦载波信息滤除，解调出间隔明显的冲击成分。图18为不同陷波参数下的时域波形。通过对比图17、18可以发现，陷波参数选择不当将导致陷波过度，冲击能量降低(ω0=50 Hz、Bw=0.6情况下)，亦或是陷波不彻底，残留趋势项(ω0=56 Hz、Bw=0.2情况下)。

进一步进行包络谱分析，分析结果如图19所示。由图19可见，利用陷波可以在原始信号包络谱图中提取到外圈故障特征频率fo及其倍频2fo分别为87.5 Hz、176.6 Hz(由于计算机进行包络谱分析时存在频谱分辨率问题，与理论计算公式计算所得的结果会有误差)，较微弱的内圈故障信息被淹没。自适应陷波后的冲击信号的包络谱可以进一步还原内圈故障的冲击特性fi为131.3 Hz(由于计算机进行包络谱分析时存在频谱分辨率问题，与理论计算公式计算所得的结果会有误差)。可见，工频干扰严重的环境下，陷波对冲击特征增强效果明显，尤其在复合故障源情况下，可以避免包络解调不足造成的故障情况误判。若进一步针对外圈故障特征频率进行陷波处理，可以从复合故障谱线中提取到明显的内圈故障频率及其倍频，如图20所示。

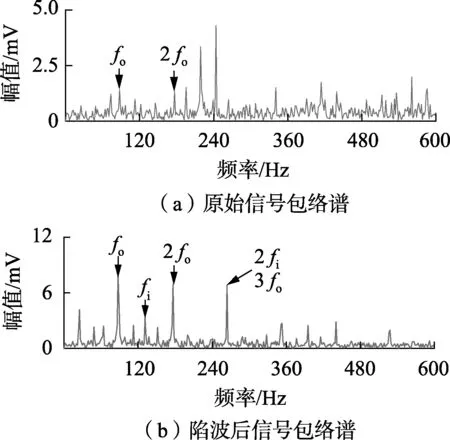
图19 滚动轴承内、外圈复合故障信号包络谱Fig.19 Spectrum envelopes of outer and inner ring compound fault signal of rolling bearing

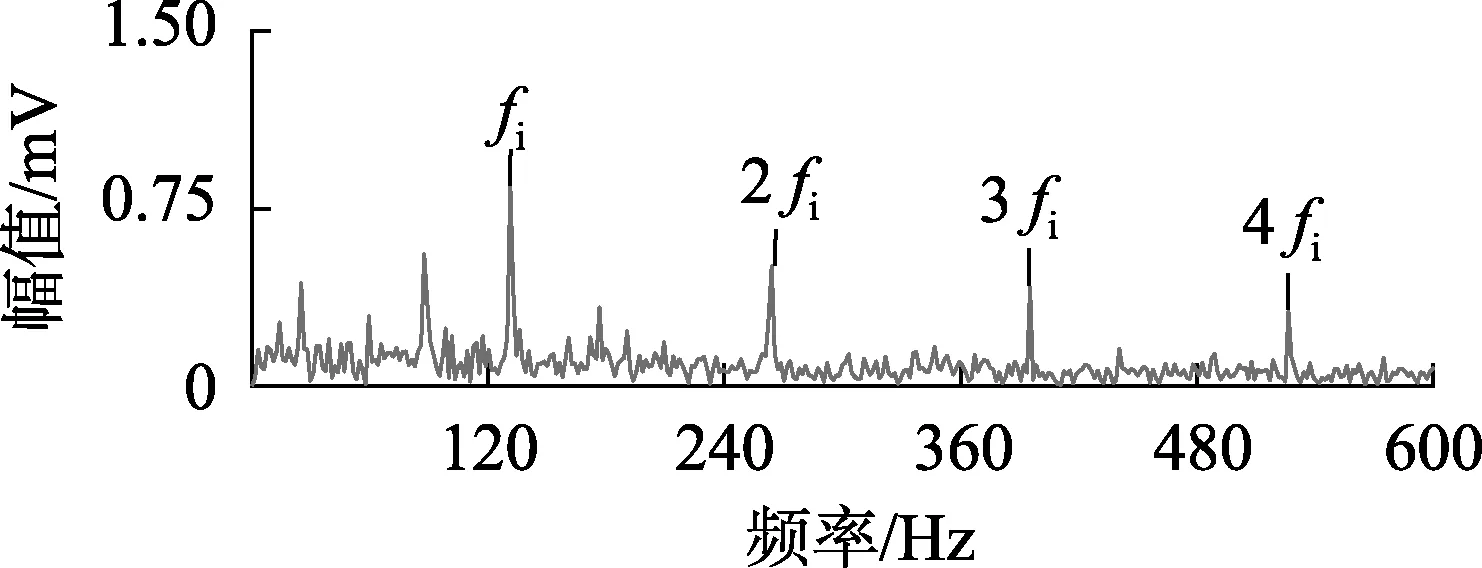
图20 内圈冲击特性包络谱Fig.20 Spectrum envelope of inner impact characteristic

4 结论

针对轴承故障诊断中调制信息易被工频载波信号淹没的问题，将工频陷波理论引入到轴承故障诊断领域。陷波消除工频干扰的参数选取只取决于转速信息，不依赖于共振频带选择，具有很好的自适应性。通过粒子群优化算法优化陷波理论中的中心频率及带宽选取方法，去除了人为因素影响，提高了陷波效率及准确性。仿真分析结果表明，利用陷波可以从工频调制信号中解调出原始冲击信息，对于工频干扰较大的工况具有明显的工频去噪效果。实验验证结果表明，利用工频陷波辅助传统信号分解降噪算法，能够准确提取淹没于噪声干扰中的冲击信息。

附录见本刊网络版(http:∥www.epae.cn)。