双端行波故障测距装置性能测试方法

冯 腾,董新洲

清华大学 电机系 电力系统及发电设备控制和仿真国家重点实验室，北京 100084)

0 引言

输电线路发生故障后所产生的暂态行波中包含了故障距离信息，因此可利用其实现精确故障测距[1-3]。近年来，电力系统中越来越多的基于行波原理的故障测距装置(以下简称行波故障测距装置)被研发和使用[4-5]。

行波故障测距原理主要分为3种[6]，即利用单端电气量的行波故障测距、利用双端电气量的行波故障测距(下文简称双端行波故障测距)和利用重合闸信号的行波故障测距。其中，双端行波测距原理简单，仅使用初始行波，易于检测，因此其测距可靠、精确度高。双端行波故障测距的缺点是需要线路两侧有准确的同步时间，但随着GPS技术在电力系统的应用，时钟同步问题已不难解决[3，6]。因此，双端行波故障测距原理现已广泛应用于各种电压等级的交直流输电线路。

为了检测行波故障测距装置的工作性能，研究者们迫切需要一种试验平台以及一套合理且完善的试验方案对其进行测试。但传统的故障检测装置测试平台(包括电力系统动态模拟、实时数字仿真器(RTDS)和传统的微机型继电保护测试仪)由于所用模型或输出频率限制等原因无法真实再现故障行波信号，因此并不适用于测试基于行波故障测距装置的性能[7]。

对于行波故障测距装置的性能测试方法，已有一些初步的探索。文献[3]中通过暂态信号发生器对双端行波故障测距装置进行了模拟试验，但该发生器输出分辨率低，且无高电压、大电流驱动能力，无法模拟互感器二次侧的行波信号。文献[8-9]中利用RTDS测试双端行波故障测距装置的性能，但由于RTDS的输出步长一般大于50 μs，需要采用补偿算法消除步长的影响，且该方法无法测试15 km以内的近距离故障。文献[10-11]采用高速行波源HSTWG(High Speed Traveling Wave Generator)测试双端行波故障测距装置，但其电流输出范围有限，对于某些严重的故障，二次侧电流可能超出其输出范围。

文献[7]研发的暂态行波保护测试仪应用多路高精度高速数模转换和宽频率功率放大技术，有效地解决了试验平台的问题。该测试仪能够真实再现电力系统二次侧的故障暂态行波信号，输出频率和幅值均满足要求。文献[12-13]研究了基于暂态行波保护测试仪的双端行波故障测距装置的测试方法，但研究不深入，对测试内容和仿真模型的分析不充分。

本文在介绍双端行波故障测距装置工作原理的基础上，分析了影响行波故障测距精度的主要因素。基于此，设计了双端行波故障测距装置的性能测试方案，研究了测试系统、测试内容以及所用的仿真模型，并重点分析了线路和二次回路的模型。最后，按照本文所设计方案对双端行波故障测距装置进行了实际测试，验证了本文所提测试方法的合理性和有效性。

1 双端行波故障测距装置的基本工作原理

双端行波故障测距装置的基本工作原理为[1-3]：在输电线路发生故障后，故障点处所产生的暂态行波将沿线路向两端变电站母线传播。利用GPS记录下故障行波初始波头到达线路两端测距装置安装处的时间，利用二者的时间差实现故障点的精确定位。

双端行波故障测距装置原理示意图如图1所示，当线路上点f发生故障时，故障行波将向两侧母线M和N传播，记录下行波初始波头到达母线M的时间tM和达到母线N的时间tN，则故障距离可通过式(1)进行计算。

(1)

其中，l为线路MN的总长；v为行波在线路上传播的波速度(下文简称波速度)；lM、lN分别为故障点到母线M、N的距离。

图1 双端行波故障测距装置原理示意图Fig.1 Schematic diagram of two-terminal traveling wave fault locator

故障行波可能来自于电流互感器(CT)或电压互感器。由于输电线路两端所安装的电流互感器可较好地传变电流行波[3，6]，因此电流行波测距装置可直接利用电流互感器的二次侧电流实现行波故障测距，这种基于电流互感器二次侧电流的行波故障测距装置在现场最为常用。

而由于电容式电压互感器(CVT)中分压电容的滤波作用，电容式电压互感器不能有效地传变高频行波信号，所以无法使用电容式电压互感器的二次侧电压信号进行行波故障测距。但考虑到电容式电压互感器地线上的入地电流为电容式电压互感器安装处电压的导数，可将故障电压行波中的高频分量保留下来，从而实现基于电容式电压互感器入地电流的行波故障测距[14]。

利用行波传感器[14]可有效地获取电容式电压互感器地线上的入地电流。行波传感器是在一根截面均匀的环形铁钴镍合金材料上均匀密绕若干层线圈而成，使用时可钳箍在电容式电压互感器的接地线上。由于其与一次系统无直接电联系，安装时无需改变一次系统接线，不会对系统运行造成影响。

2 双端行波故障测距精度分析

为了设计合理有效的双端行波故障测距装置的性能测试方案，首先需对影响双端行波故障测距精度的主要因素进行研究。

文献[15]分析了影响输电线路行波故障测距精度的主要因素，指出雷击、故障时电压相角、故障类型和位置以及母线和线路类型均会对行波故障测距产生影响。下文将从装置性能测试的角度出发，由双端行波故障测距的原理公式入手分析故障测距精度的影响因素，为双端行波故障测距装置的性能测试方案的设计提供参考。

双端行波故障测距的原理比较简单，由式(1)可知，故障距离可利用线路总长、波速度和行波初始波头到达线路两端母线的时间共4个物理量计算得到。其中，行波初始波头到达线路两端母线的时间由双端行波故障测距装置测量得到，而线路总长和波速度为装置的定值。双端行波故障测距装置能否准确获取或设定上述物理量将直接影响故障测距的精度。

2.1 线路总长

由于弧垂的存在，线路的实际总长无法精确获取。由于弧垂随外界因素(特别是环境温度)的变化而改变，这使得线路总长不再是一个定值，会影响测距的精度。

2.2 行波在线路上的传播速度

由于导线和大地在交变电磁场作用下具有集肤效应，输电线路的电阻和电感随电流频率而变化，成为频变参数。此时线路对于各个不同频率分量呈现出不同的传输特性，将会直接影响暂态行波的特性。

单位长度线路串联阻抗矩阵Z为：

Z=Zex+Zin=Zg+Ze+Zin

(2)

其中，Zex为导线外阻抗矩阵，其包含了导线和大地均为理想导体时的回路阻抗矩阵Zg(纯电感)和大地的内阻抗矩阵Ze两部分，Zg和Ze为对称的满阵；Zin为内阻抗矩阵，其为对角阵。

易求得Zg的元素为：

(3)

(4)

其中，μ0为真空磁导率;xi和xj分别为第i个和第j个导体的横坐标；yi和yj分别为第i个和第j个导体的纵坐标；ri为第i个导体的半径。

Ze的元素可利用Dubanton公式[16]求得：

(5)

(6)

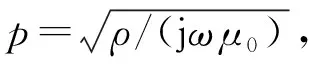
此时有：

(7)

Zin的对角元素可采用Bessel函数进行计算[17]，对于实心圆柱导体，其内阻抗为：

(8)

综上所述，单位长度线路串联阻抗矩阵Z中的元素为：

(9)

波速度与单位长度的线路串联电感和并联电容有关，单位长度线路串联电感的依频特性使行波中的不同频率分量在线路上的传播速度不同。

采用一个水平分布并均匀循环换位的三相线路结构进行分析，其参数详见附录。可计算得到线模波速度随频率变化的曲线如图2所示。

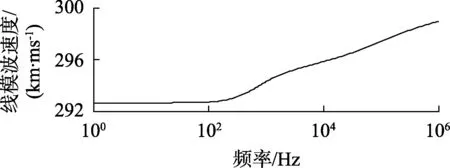
图2 线模波速度随频率变化的曲线Fig.2 Line mode wave velocity varying with frequency

在设定双端行波故障测距装置所用的波速度定值时，应首先确定装置所用信号的频率，再根据线路的物理参数(几何尺寸、导体和大地电阻率等)精确计算该频率下的波速度。波速度如果设定不准确将影响测距的精度。对于一条长300 km的线路，若线路波速度定值的误差为1 km/ms，则其测距误差最大可达500 m。

2.3 行波初始波头到达母线的时间

由于行波初始波头到达两侧母线的时间是由双端行波故障测距装置测量得到的，因此，需要考虑哪些因素会对行波初始波头的准确识别产生影响。

a. 行波初始波头的形态。

2.2节中的分析表明，线路参数的依频特性使行波不同频率分量的波速度不同，从而对行波初始波头的形态产生影响，使其发生畸变，跳变“变缓”，增加识别难度。而且，随着故障点与母线距离的增加，畸变变得更加严重，对行波初始波头的准确识别也更加困难。

此外，双端行波故障测距装置的输入信号通常取自于电力互感器——电流互感器二次侧电流或电容式电压互感器地线上的入地电流。电力互感器将一次侧的高电压、大电流变换为二次侧的较低电压、较小电流，其传变特性会对行波初始波头的形态产生一定的影响。

b. 行波初始波头的大小。

文献[7]推导了模域的电压电流初始行波计算公式。当线路电压等级和线路参数确定时，故障初始行波受故障类型、故障过渡电阻和故障初相角的影响。

c. 行波初始波头与后续折反射波的叠加。

由于双端行波故障测距装置安装处与母线十分靠近，其检测到的行波波头是由故障初始行波和母线的反射行波叠加而成。因此，母线结构亦会对其产生影响。由于故障行波会在母线、故障点等波阻抗不连续处发生折反射，当故障点靠近母线或线路本身较短时，初始波头与后续的折反射波相互叠加，会对双端行波故障测距装置产生影响。

另外，在电力互感器的二次侧，由二次电缆将电力互感器二次侧电流传输至故障测距装置。由电力互感器和二次电缆组成的二次回路的传变特性并不理想，会使行波波头发生畸变，进而影响故障测距精度。

综上所述，影响测距准确性的因素包括线路自身特性、故障类型、故障位置、故障过渡电阻、故障电压初相角以及母线结构。另外，二次回路(包括电力互感器和二次电缆)也会影响故障测距的准确性。

3 双端行波故障测距装置性能测试方案

3.1 测试系统与测试步骤

双端行波故障测距装置性能测试的关键在于模拟不同故障下电力互感器二次侧的电流行波。为此，需考虑2个问题：一是在设计测试方案时考虑各种可能对故障测距精度产生影响的故障，以保证测试的全面性；二是寻求能够真实输出电流行波模拟量的测试平台，以保证测试的有效性。对于前者，将在3.2节中进行讨论。对于后者，暂态行波保护测试仪的成功研发有效解决了该问题。该测试仪的故障数据来源可为电力系统现场的故障录波数据或电磁暂态仿真软件的故障仿真数据[7]。受录波器采集回路传变特性及模数转换采样精度的影响，使用现场录波数据进行测试效果并不理想，且现场故障次数极少，无法保证测试的全面性。因此，选择利用仿真软件建立输电系统仿真测试模型，构建故障数据库。

基于暂态行波保护测试仪的双端行波故障测距装置性能测试系统示意图如图3所示。

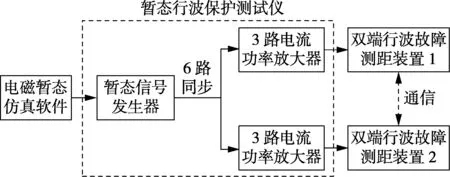
图3 双端行波故障测距装置性能测试系统示意图Fig.3 Schematic diagram of performance test system of two-terminal traveling wave fault locator

具体测试步骤如下：

a. 在电磁暂态仿真软件(如EMTP)中建立仿真测试模型并进行不同故障的仿真；

b. 将EMTP 生成的仿真测试数据转换成暂态行波保护测试仪可使用的测试文件格式，并下传至暂态信号发生器；

c. 暂态信号发生器通过数模转换，输出6路同步的模拟电压小信号，6路信号通过电流功率放大器放大后模拟电力互感器二次侧的电流，并输出至被测装置。

3.2 测试内容

双端行波故障测距装置性能测试分为基本故障测试和特殊故障测试。根据上文的结论，在基本故障测试中，应对不同类型线路(包括单回长线、单回短线、双回长线、双回短线)和母线结构下双端行波故障测距装置的可靠性和故障测距精度进行全方位的试验。针对每种电网结构，全面检测了双端行波故障测距装置在不同故障类型、不同故障位置、不同故障初相角和不同故障过渡电阻下的性能。

除了上述基本故障外，为保证测试的全面性，还应考虑一些特殊类型的故障。特殊故障测试应包括双端行波故障测距装置在断线故障、转移性故障、故障过渡电阻时变、频率偏移、跨线故障(针对同杆双回线)等特殊故障下的故障测距性能。

3.3 系统整体模型

为了更加精确地模拟电力系统故障行波，最理想的状态应该是搭建电力系统的完整模型，但这显然是不现实的。因此，需对系统模型进行适当的简化与等值。根据所研究的电力系统的特点，将整个网络分为核心区、周边区和外围区。核心区对研究对象的电磁暂态有很大的影响，需要精确建模，强调计算精度;周边区对研究对象电磁暂态影响不大，可以建立适当简化的模型，综合考虑计算精度和计算时间;外围区对研究对象的电磁暂态影响较小，可以建立简化的等值电路。

对于输电系统故障行波仿真，所研究的电力系统网络的核心区应为双端行波故障测距装置所安装的线路及其相邻变电站。在建模过程中，应采用精确的线路模型，考虑依频参数，考虑避雷线等线路中的其他结构对故障行波的影响。对于相邻变电站，应全面考虑站内各电力设备的电磁暂态模型，如电力互感器以及电力互感器所连接的二次电缆等。

周边区应包含与故障测距装置所安装的线路直接相连的线路。这些线路的建模可以模拟行波在变电站母线处的折反射过程，还可以通过将故障设置在这些线路上对区外故障进行仿真。对于距离故障测距装置更远的线路，其反射回来的行波较小，且行波经过较长距离的传播，线路的电阻会使其高频分量发生较大的衰减。

外围区包含除核心区和周边区以外的系统其余部分，可采用电源和阻抗进行等效。此部分对行波的传播过程影响不大，更多的是对故障后的稳态产生影响。

仿真系统模型如图4所示。仿真系统模型中，双端行波故障测距装置安装在线路L上，整个电力网络的核心区为线路L和母线M、N，其他各条线路为周边区，可用于模拟行波的折反射，各电源及阻抗为外围区，可用于等效系统中的其余部分。

图4 仿真系统模型Fig.4 Simulation system model

4 测试数据仿真中的关键元件模型

在仿真生成故障测试数据时，应尽量真实完整地再现现场故障时的行波过程。因此，仿真时应尽量使用电力系统各元件的宽频暂态模型，并尽可能全面地考虑会对行波特性产生影响的各个因素。

4.1 输电线路模型

初始电压行波的复频域值为U(ω)，其在输电线路上传播至距离其lt处后的复频域值为Ult(ω)。Ult(ω)与U(ω)的关系如下：

Ult(ω)=U(ω)e-γ(ω)lt

(10)

其中，γ(ω)为行波在线路上的传播系数，计算公式如式(11)所示。

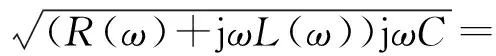
α(ω)+jβ(ω)

(11)

其中，R(ω)、L(ω)和C分别为线路单位长度的串联电阻、串联电感和并联电容；α(ω)和β(ω)分别为线路的衰减系数和相位系数。式(11)忽略了线路的对地电导，并认为对地电容参数不随频率变化，R(ω)、L(ω)的频变特性可由式(9)求得。

指数函数反映了行波传播过程中的延时、衰减和畸变，行波传播距离lt需一定的时间，且由于线路参数随频率变化，不同频率的波传播的速度不同，使波形发生畸变。由于串联电阻的存在，行波还存在幅值上的衰减。

因此，为了更加真实地模拟电力系统现场故障后暂态行波的特性，在仿真生成故障测试数据时采用考虑了频变参数的线路模型。

4.2 电流互感器模型

图5为电流互感器的等值电路模型[18]，图中的参数都已折算到二次侧。图中，R1和L1为一次侧的电阻和电感；R2和L2为二次侧的电阻和电感；RL和LL为负载的电阻和电感；Rm为铁芯磁化电阻，Lm为铁芯磁化电感，具有非线性饱和特性；n为变比。

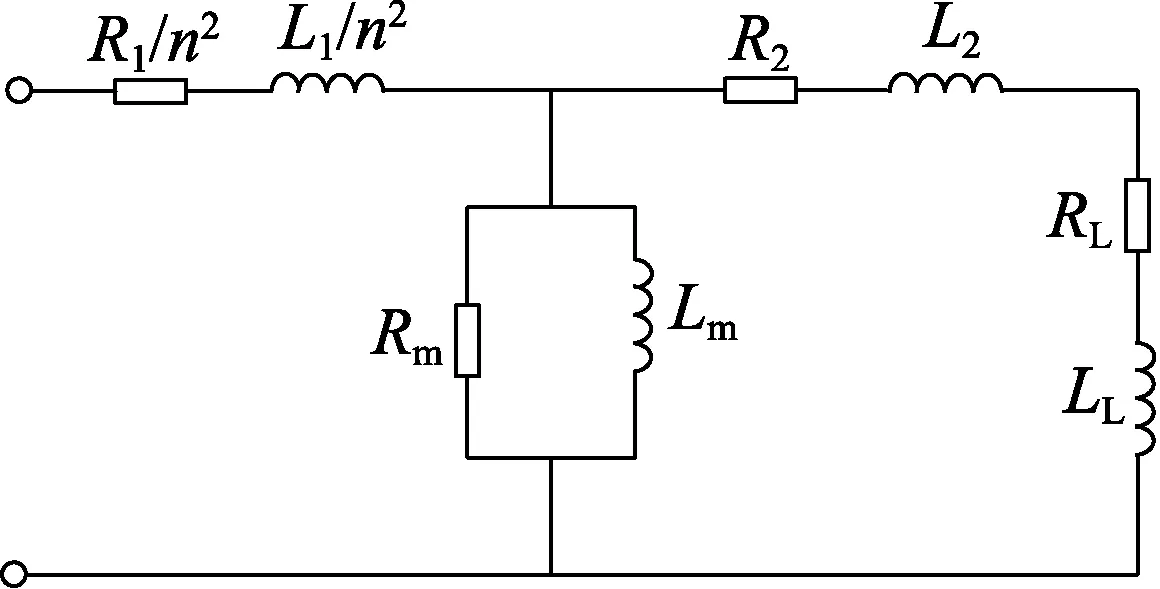
图5 电流互感器模型Fig.5 Model of current transformer

电流互感器等值模型中的电流传输函数(未考虑变比)为：

(12)

其中，K=RmLm+(R2+RL)Lm+Rm(L2+LL)。

由于Rm≫R2+RL、Lm≫L2+LL，传递函数可化简为：

(13)

式(13)为一增益为1的带通滤波器，可求出其截止频率、下限截止频率和上限截止频率分别为：

(14)

(15)

(16)

通常情况下，铁芯磁化电阻Rm约为几千欧姆，铁芯磁化电感Lm约为几亨到几十亨，二次侧的电阻R2约为几欧姆，二次侧的电感L2约为零点几毫亨到几毫亨，负载的电阻和电感RL和LL在不考虑二次电缆时为测距装置的电流互感器输入阻抗，一般仅为毫欧级和微亨级，较二次侧的电阻和电感分别小2、3个数量级，因此可以忽略。因此，在不考虑二次电缆时，下限截止频率一般为零点几赫兹到几赫兹，远小于工频。二次电缆的长度一般不会超过1 km，其电阻值不会超过几欧姆，下限截止频率会随二次电缆长度的增加而略有提升，但仍会远小于工频。而上限截止频率在不考虑二次电缆时一般为几百千赫兹到几兆赫兹，且会随二次电缆长度的增加而略有下降，可能会降至几十千赫兹，此时，会对双端行波故障测距装置产生影响。

因此，在对电流互感器进行电磁暂态建模时，应特别注意铁芯磁化电阻Rm和二次侧的电感L2的参数获取。

另外，经过上述分析可知，电流互感器二次侧所接的二次电缆在仿真中也应被着重考虑，特别是其长度将会对电流的传变产生较大的影响。下面分析二次电缆的模型选择。由于二次电缆一般较短，可使用集总参数进行建模。若电缆的单位长度电容为150 nF/km、单位长度电感为0.3 mH/km，对于频率为100 kHz的信号，当电缆长度大于150 m时，电容的阻抗值就已小于电感的阻抗值，分流电容支路不可忽略。因此，除非电缆线路极短(如只有几米)，否则其电容不可忽略。

绘制不考虑电流互感器及其二次电缆和考虑电流互感器及其二次电缆影响时的故障电流行波波形如图6所示。从图中可以看出，电流互感器及其二次电缆的存在会对行波波头的形态产生影响，增加识别难度，影响故障测距精度。

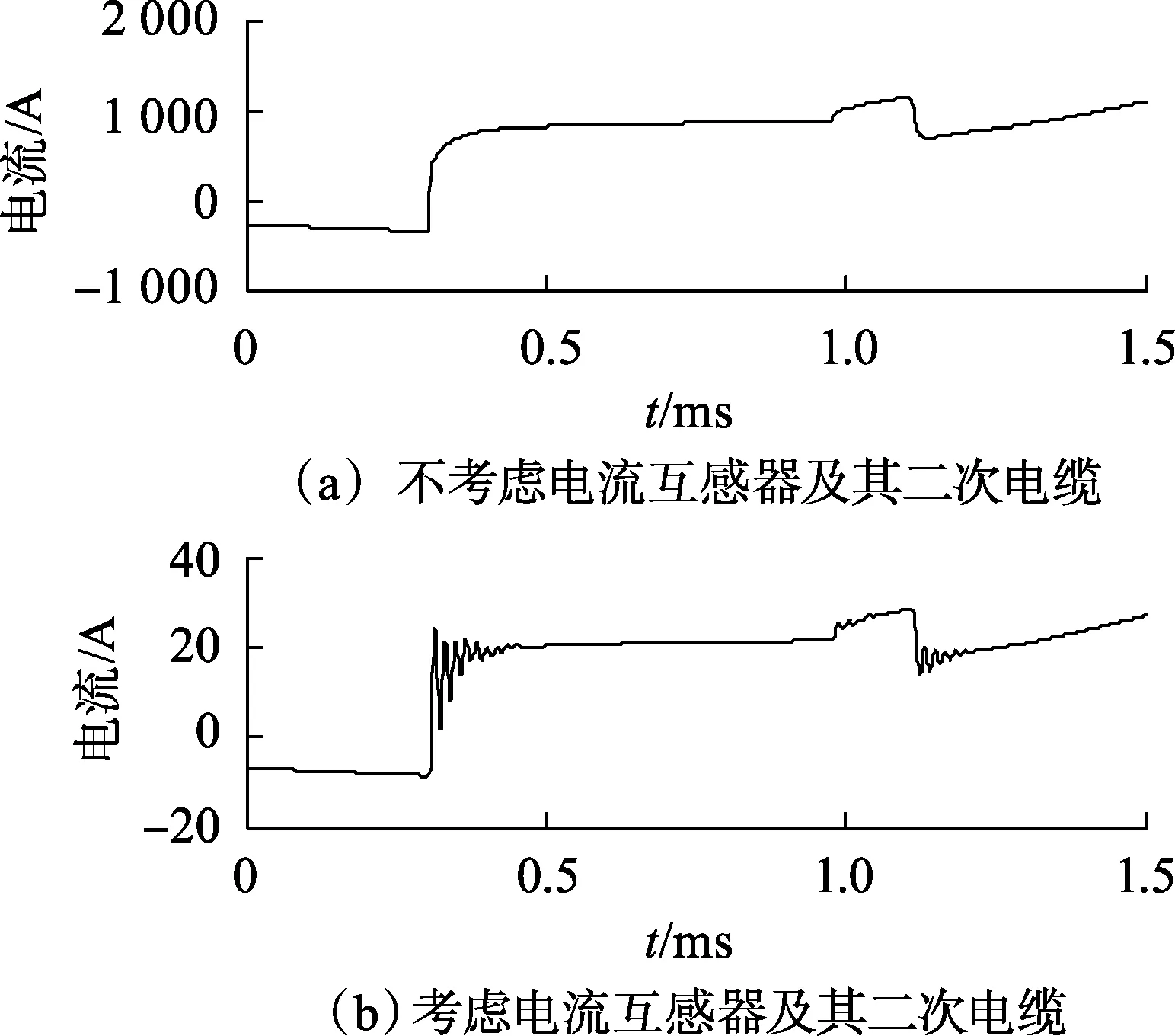
图6 电流互感器对故障电流行波的影响Fig.6 Influence of CT on fault current traveling wave

4.3 电容式电压互感器模型

对于利用电容式电压互感器地线的入地电流的故障测距装置，需考虑电容式电压互感器的电磁暂态模型。

图7为电容式电压互感器的等值电路模型[18]。图中，C1和C2为分压电容；I为入地电流；Lt、Rt和Ct分别为补偿电抗器的电感、电阻和杂散电容；Cp为一次侧的杂散电容；Rm和Lm分别为铁芯磁化电阻和磁化电感，具有非线性饱和特性；谐振阻尼器选择谐振型阻尼器，Rf和Lf分别为其电阻和电感。

图7 电容式电压互感器模型Fig.7 Model of capacitor voltage transformer

分析电容式电压互感器的入地电流I关于线路电压的传递函数，绘制其频率特性曲线如图8所示。

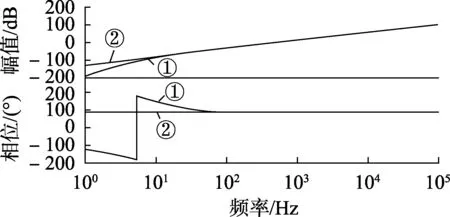
①—考虑完整的电容式电压互感器模型 ②— 仅考虑电容分压器部分图8 电容式电压互感器入地电流的频率特性曲线Fig.8 Frequency characteristic curve of CVT’s grounding current

从图中可以看出，在电容式电压互感器模型中，电容分压器以外部分对入地电流的影响主要集中在低频段，对工频及以上频率的影响可以忽略。因此，在获取电容式电压互感器地线的入地电流时，可仅考虑电容分压器部分，即仅考虑C1和C2。

此外，电容式电压互感器中可能存在用于载波通信的排流线圈Ld(如图9所示)[19]，也应给予考虑。综上，可通过仿真电容式电压互感器安装处经分压电容和排流线圈接地后的电流获取电容式电压互感器的入地电流。

图9 电容式电压互感器中的排流线圈Fig.9 Drain coil in CVT

5 测试方案的实际应用

根据3.2节中的测试内容对双端行波故障测距装置进行了大量的测试，被测装置的暂态行波故障信息采样率为1 MHz，同步误差小于1 ms。测试中的一些典型情况如表1所示。其中，系统模型中，母线M、N之间仅存在一条长400 km的单回线，且两母线的出线数均为3，如图10所示。

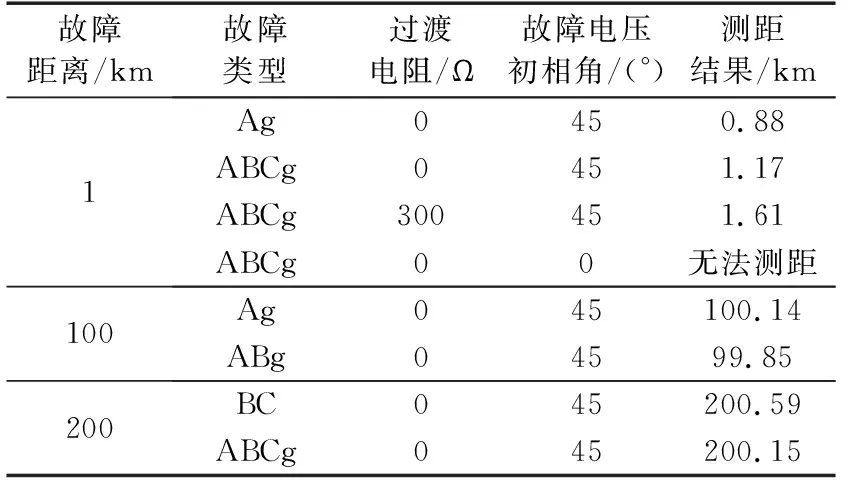
表1 测试结果Table 1 Test results

图10 系统模型Fig.10 System model

本文所提测试方法可针对各种不同类型的故障情况对被测装置进行测试，并能发现被测装置存在的不足，如当故障电压初相角过小时，行波波头幅值较小，不易被被测装置检测到，导致无法测距。

①— 母线M处的A相电流②— 母线N处的A相电流图11 仿真数据和双端行波故障录波数据的对比图Fig.11 Comparison between simulative data and data recorded by two-terminal traveling wave fault locator

选取某次测试中两侧母线的A相波形进行对比分析。该次测试中，距母线M100 km处发生A相金属性接地故障，故障时A相电压相角为45°。图11为仿真数据和双端行波故障测距装置录波数据的对比图。从图中可以看出，二者波形十分相似，仅在一些细节(如二次回路导致的振荡)上有所差别，这是由于测试仪输出频率及双端行波故障测距装置采样频率的限制所导致的。二者波形的近似既证明了暂态行波保护测试仪作为检测工具的有效性，又证明了被测的双端行波故障测距装置工作的正确性。

6 结论

双端行波故障测距装置利用故障行波初始波头到达线路两端故障测距装置安装处的时间差实现故障点的精确定位。影响故障测距准确性的因素包括线路自身特性、故障类型、故障位置、故障过渡电阻、故障电压初相角、母线结构及二次回路。可使用暂态行波保护测试仪对双端行波故障测距装置进行性能测试，测试时应全面考虑上述影响因素。此外，为保证测试的全面性，还应考虑一些特殊类型的故障。

在仿真生成故障测试数据时，应真实再现现场故障的行波过程。对于输电线路，应考虑参数的频变特性。对于电流互感器，应使用宽频带暂态模型，并考虑二次电缆的影响。若双端行波故障测距装置使用的是电容式电压互感器入地电流，在仿真时只需考虑电容式电压互感器的电容分压器部分和排流线圈即可。

对于本文所提测试方法，今后还需要在以下方面进行进一步的研究：

a. 研究电力系统中除线路和电力互感器之外的其他电气设备的宽频带暂态模型；

b. 对于电力互感器模型，仿真中使用的虽是常用的暂态模型，但一些参数，特别是杂散电容等，与线圈匝数和绕制方式有关，仿真时均使用估值，在今后的研究中应考虑如何确定其较为准确的取值；

c. 测试方案中虽然考虑了弧垂，但仍需研究弧垂随外界因素的变化情况；

d. 对于线路模型，其参数应尽量与现场吻合，需研究在线路爬坡等实际中可能存在的情况下应如何建模。

附录见本刊网络版(http:∥www.epae.cn)。