光伏电站直流汇集接入系统的建模分析

戴志辉，朱惠君，严思齐，苏怀波，贾 科

1. 华北电力大学 河北省分布式储能与微网重点实验室，河北 保定 071003；2. 华北电力大学 新能源电力系统国家重点实验室，北京100084)

0 引言

预计到21世纪末，全球能源需求将达到目前的3倍[1]。其中，电能在衡量经济发展水平的同时，也影响着经济的发展[2]。目前，仍然存在部分地区难以接入现有电网的现象，这在一定程度上影响了当地经济的发展[3]。以太阳能和风能为代表的可再生能源发电技术的发展，为缓解地区并网压力提供了一种解决方案。由于可再生能源发电具有间歇性、波动性和不确定性等特点，需要设计合理的能源接入系统方式，提高电网接纳清洁能源的能力[4]。

传统的光伏交流接入系统主要包括光伏电站、DC/DC变流器、DC/AC并网变流器及滤波器4个部分[5]。其中，DC/DC光伏变流器一般采用Buck电路，主要用于控制光伏电站工作在最大功率点处，并维持电压相对稳定；DC/AC并网变流器一般采用脉宽调制(PWM)控制的电压源型换流器(VSC)，主要用于将直流电变为与电网电压幅值相等的工频交流电，并承担大部分升压工作[6]。

光伏直流接入系统的组成与交流接入系统基本相同，但DC/DC变流器不仅具有最大功率控制作用，还承担部分升压工作。多个光伏电站级联能提高光伏输出电压，并维持电压稳定，从而实现光伏发电的直流输送[7]。由于光伏输出为直流电压，且可采用电压较低的隔离型光伏变流器抑制共模漏电流，所以采用直流接入方式可降低控制的复杂度，减少变流器级数，减少隔离变压器损耗，提高光伏发电效率[8-9]。相比于交流输电，中高压直流输电损耗较小，采用直流接入方式更有利于光伏的接入。但采用光伏级联直流接入方式时，由于光伏电池的辐照度不同，为了顺利实现并网及最大功率点跟踪控制，需注意各光伏并网变流器之间的均压问题[8]。

本文研究了光伏直流汇集接入方式及其分析模型的建立。其中，并网变流站采用箝位双子模块型模块化多电平变流器(CDSM-MMC)，通过最近电平逼近法得到桥臂投入子模块数，结合电容电压排序确定投切的子模块，实现子模块均压[10]；光伏变流站由并联输入串连输出(IPOS)结构的多模块Boost全桥隔离变流器(BFBIC)组成，相比于传统的光伏接入方式，并联输入使得各光伏并网变流器输入电压相同，串联输出使得光伏电站输出电压提高，在满足升压要求的同时，缓解了辐照度不同导致的各个光伏并网变流器输出电压不平衡问题[11-12]。有关BFBIC实现光伏最大功率控制的文献较少，本文设计了最大功率定电压控制BFBIC中Boost部分的控制方案。通过与定输出电压控制Boost部分、最大功率定电压控制有源箝位部分的方案进行仿真对比，验证了最大功率定电压控制Boost部分可实现光伏最大功率控制；并结合仿真结果，给出了不同控制方式的使用建议。

1 光伏直流汇集接入系统的PSCAD模型

1.1 光伏电池组模型

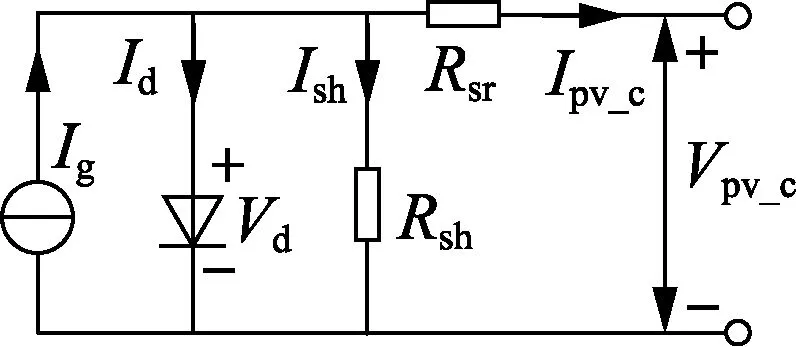
图1 光伏电池单元等效电路Fig.1 Equivalent circuit of photovoltaic cell

本文建立的光伏电池模型为2层结构：第一层为电池单元，第二层为电池模块。等效电流源Ig、串联等效电阻Rsh、并联等效电阻Rsr和二极管构成电池单元等效模型，如图1所示。电池单元输出电流为：

Ipv_c=Ig-Id-Ish

(1)

其中，Ipv_c为光伏电池单元输出电流；Id为二极管电流；Ish为并联电阻电流。

根据二极管的伏安特性方程，可得电池单元的输出特性如式(2)所示[13]。

(2)

其中，Io为二极管反向饱和电流；Vpv_c为光伏电池单元输出电压；nd为二极管特性因子，一般取1～2；k为玻尔兹曼常数，取1.38×1023J/K；τc为光伏电池温度；q为电子的电荷量，取1.6×10-19C。

本文方案中，电池单元经串并联组成电池模块，且每个电池模块最多包含20×20个电池单元。电池模块经串并联组成光伏电池模型。通过调整串联电池单元及电池模块数量，达到调整光伏电池模型开路电压的目的；通过调整并联电池单元及电池模块数量，达到调整光伏电池模型容量的目的。光伏电池输入为辐照度及温度。

1.2 光伏直流并网变流站模型

光伏直流并网变流站采用以BFBIC为基本单元的2级结构：采用IPOS结构的多个BFBIC组成第一级结构，称为IPOS模块；多个IPOS模块并联构成第二级结构，即一个光伏变流站。图2为光伏变流站拓扑结构示意图。

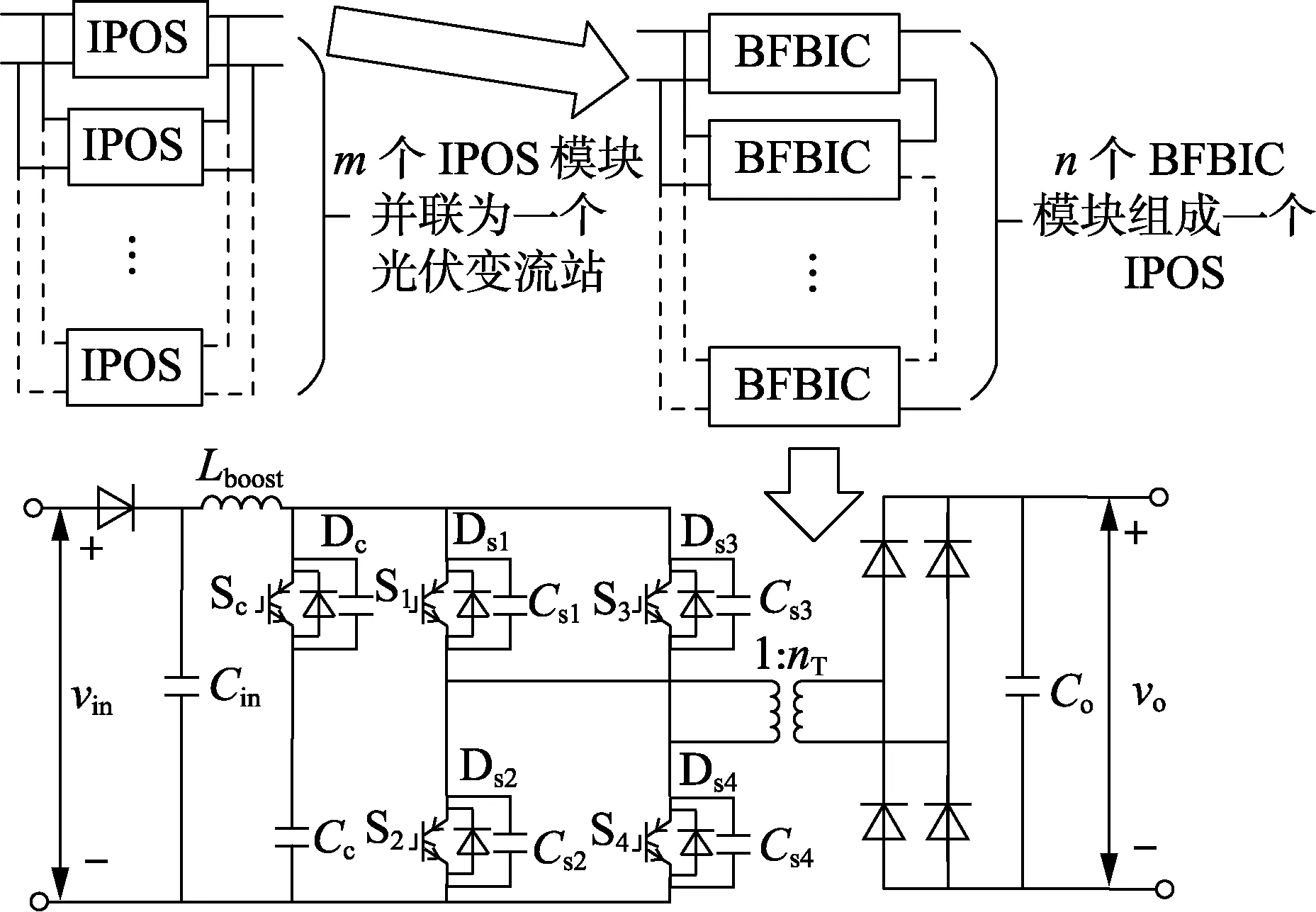
图2 光伏变流站拓扑结构Fig.2 Topology of photovoltaic converter station

BFBIC拓扑中，Lboost为升压电感；vin为输入电压；Cin为储能电容；Cc为箝位电容；Co为滤波电容；vo为输出电压；变压器变比为1∶nT。与传统Boost拓扑相比，BFBIC通过升压电感与高频变压器共同实现升压功能，缓解了变压器的升压压力；箝位电容可吸收开关管投切时的电压尖峰，减小开关管的电压应力；采用统一信号控制且输出经滤波电容，实现电压自均衡。

1.3 交流并网变流器模型

交流并网变流器采用CDSM-MMC拓扑结构。可以将主回路分成3级，由上级到下级分别是MMC换流器级、MMC桥臂级和CDSM模块级。各级对应的控制功能见表1。

表1 MMC模块各层级控制功能Table 1 Control functions of all levels for MMC module

图3为CDSM-MMC拓扑结构示意图[14]，MMC变流站由6个桥臂、6个桥臂电感Larm、滤波装置、充电电阻Rl和1台三相交流变压器构成，图中N为除去冗余模块后各相CDSM个数。

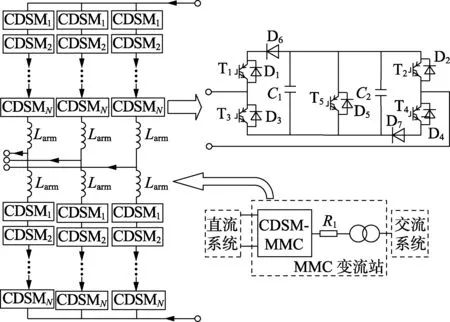
图3 CDSM-MMC变流站拓扑结构示意图Fig.3 Topology of CDSM-MMC converter station

2 控制系统模型

2.1 光伏直流并网变流站控制系统模型

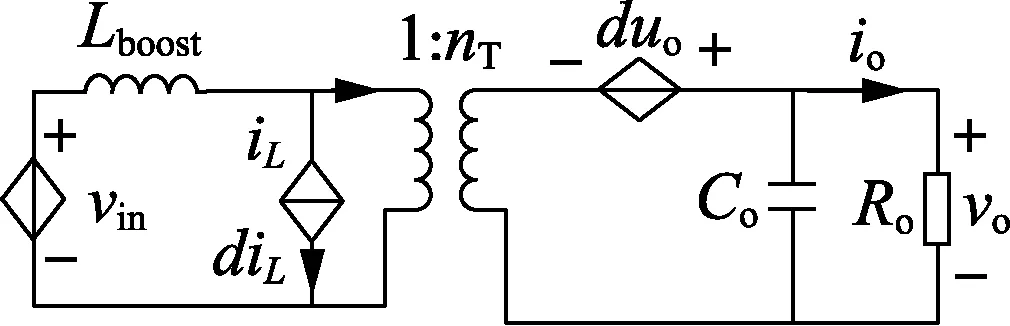
图4 BFBIC的时域等效模型Fig.4 Time-domain equivalent model of BFBIC

为得出光伏变流站系统传递函数框图，先分析BFBIC的小信号模型。图4为BFBIC的时域等效模型[11-12]。图中，vin为BFBIC输入电压瞬时值，且受光伏输入辐照度及温度控制，满足光伏输出电流-电压特性；iL为升压电感电流瞬时值；d为S1—S4触发信号占空比瞬时值；io为BFBIC输出电流瞬时值；vo为BFBIC输出电压瞬时值；Ro为等效负载。

根据基尔霍夫定律，有：

(3)

其中，iin为BFBIC输入电流。

进而得到s域上的小信号模型为：

(4)

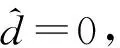
(5)

同理，可得输出电压与占空比的传递函数为：

(6)

令：

(7)

G1(s)=nT/(1-D)

(8)

G2(s)=Vo-s[nTILLboost/(1-D)2]

(9)

则式(5)和式(6)可分别写为：

(10)

(11)

结合BFBIC的工作原理[12]，设计了2种控制方案，如图5所示。

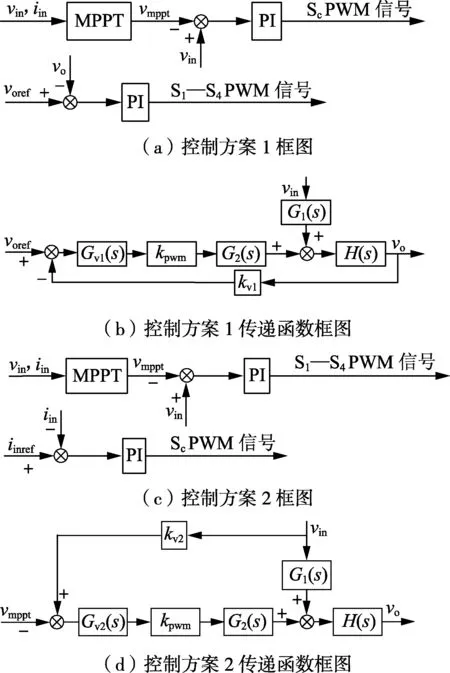
图5 BFBIC控制系统框图Fig.5 Block diagram of BFBIC control system

方案1的控制系统框图如图5(a)所示。最大功率定电压控制Sc，实现变压器一次侧电压箝位；定BFBIC输出电压，即光伏变流站输出电压控制S1—S4，稳定变流站输出电压。其中，voref为BFBIC输出电压参考值；vmppt为最大功率定电压控制的输出参考电压；控制S1— S4PWM信号的PI控制器比例系数为kvp1，积分常数为kvi1。PI控制电压环回路方程为：

ue1(s)=[voref(s)-vo(s)](kvp1+kvi1/s)

(12)

其中，ue1为采用控制方案1时S1—S4触发信号的PWM波。

对式(12)进行线性化处理，得到ue1小信号模型为：

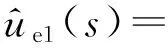
(13)

从而得到控制方案1的系统传递函数框图，如图5(b)所示。其中，产生PWM波的传递函数可以近似为常系数kpwm。

方案2的控制系统框图如图5(c)所示。定光伏输出电流，即BFBIC输入电流控制Sc，实现变压器一次侧电压箝位；最大功率定电压控制S1— S4，实现光伏电池输出电压跟踪最大功率点电压值。其中，iinref为BFBIC输入电流参考值；控制S1— S4PWM信号的PI控制器比例系数为kvp2，积分常数为kvi2。最大功率点跟踪控制电压环回路方程为：

ue2(s)=[vmppt(s)-vin(s)](kvp2+kvi2/s)

(14)

其中，ue2为采用控制方案2时S1— S4触发信号的PWM波。

对式(14)进行线性化处理，得到ue2小信号模型为：

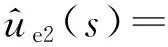
(15)

从而得到控制方案2的系统传递函数框图，如图5(d)所示。

2.2 交流并网变流器控制系统模型

MMC控制包括上下桥臂导通子模块数的计算及调制波的产生两部分。导通子模块数的计算采用最近电平逼近法实现[10]；调制波的产生通过矢量控制实现。基于最近电平逼近法的上下桥臂导通子模块数的计算公式如式(16)所示。

(16)

其中，Ue为MMC调制波；Uc为MMC子模块电容电压；round(x)表示取与x最接近的整数。

当MMC输入发生扰动时，为维持输出稳定，MMC的整体控制采用经典的双闭环直接电流矢量控制方式，图6为MMC控制系统框图。图中，Udc为直流侧电压；Udcref为直流侧电压参考值；Qs为交流侧无功功率；Qsref为交流侧无功功率参考值；Idref为交流侧d轴电流参考值；Iqref为交流侧q轴电流参考值；Id为交流侧d轴电流；Iq为交流侧q轴电流；Usd为交流侧d轴电压；Usq为交流侧q轴电压；Udref为交流侧d轴电压参考值；Uqref为交流侧q轴电压参考值。外环采用定直流电压与交流无功功率控制，内环采用交流电流矢量解耦控制，控制器输出MMC调制波Ue[15]。

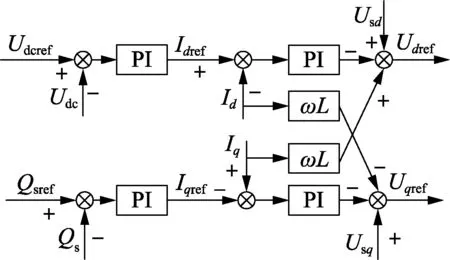
图6 MMC控制系统框图Fig.6 Block diagram of MMC control system

3 算例分析

以某市一光伏电站为例，当光伏变流站采用不同的控制方案时，对比分析系统的抗光照干扰能力以及光伏电能送出能力。日均净辐照度约为637.45 MJ/m2，日平均气温约为14.9 ℃。光伏电站包括±30 kV/1.5 MW集中式及20 kV/500 kW集散式电站2种。光伏变流站采用IPOS方式连接的BFBIC拓扑结构，且每个BFBIC输出电压为5 kV。光伏电池输出电压经变流站升压后，汇集接入±30 kV直流电网。交流并网变流器采用9电平CDSM-MMC拓扑结构，±30 kV直流电网经过10 km电缆后，与35 kV交流系统通过交流并网变流器连接，如图7所示。

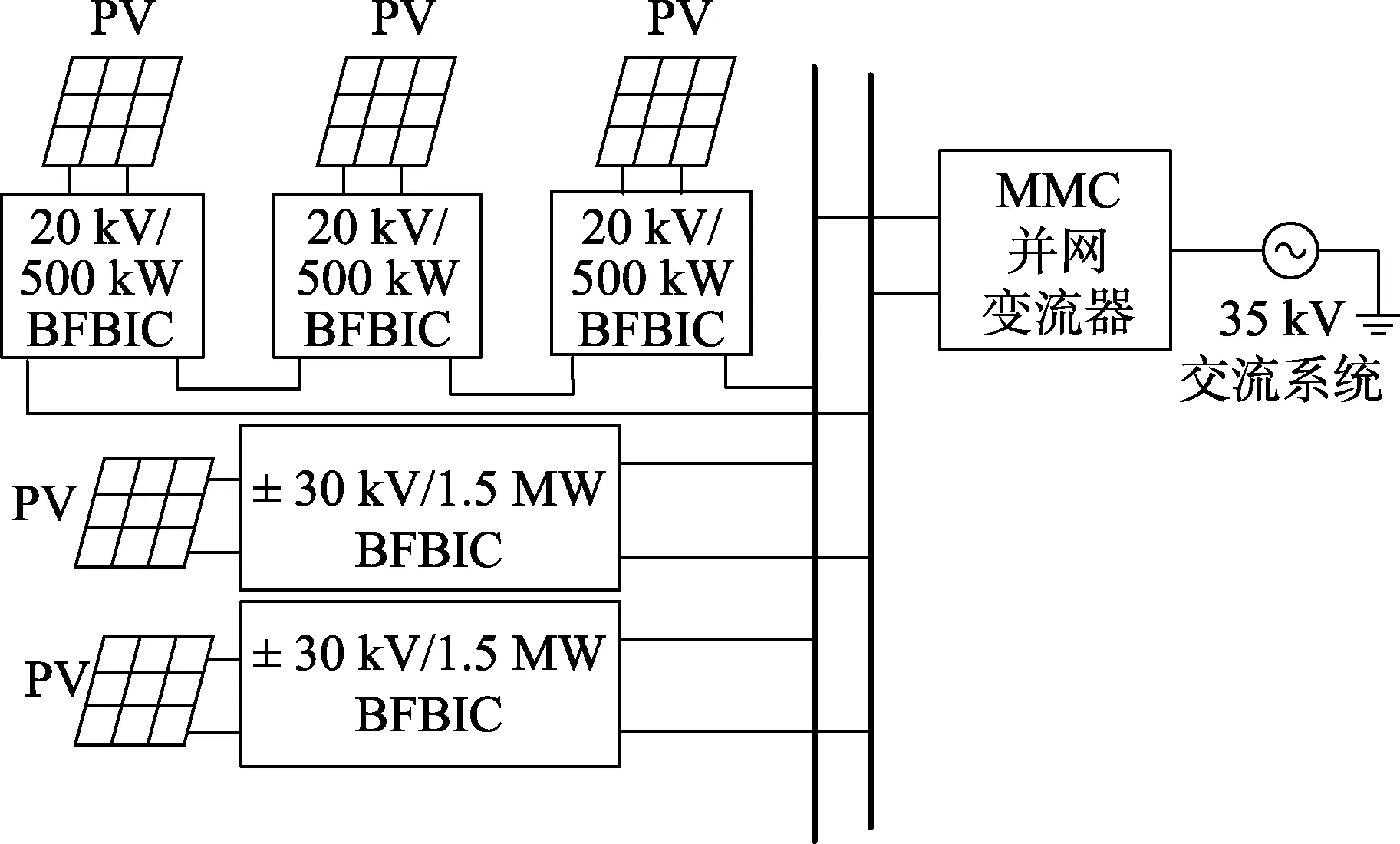
图7 光伏直流汇集接入系统拓扑图Fig.7 Topology of DC convergence integration system of photovoltaic power generation

3.1 孤岛运行的仿真分析

图8(a)、(b)分别为使用控制方案1时光伏变流站正极输出电压和有功功率波形图。仿真初始时光伏电池投入运行，1 s时改变光伏电池输入辐照度与温度。由图8(a)、(b)可知，光伏变流站输出电压响应时间约为0.5 s，电压峰值约为33.4 kV，超调量约为11%。1 s时改变光伏输入量，调整时间约为0.25 s，电压超调量约为2%，输出有功功率基本稳定在2.5 MW。

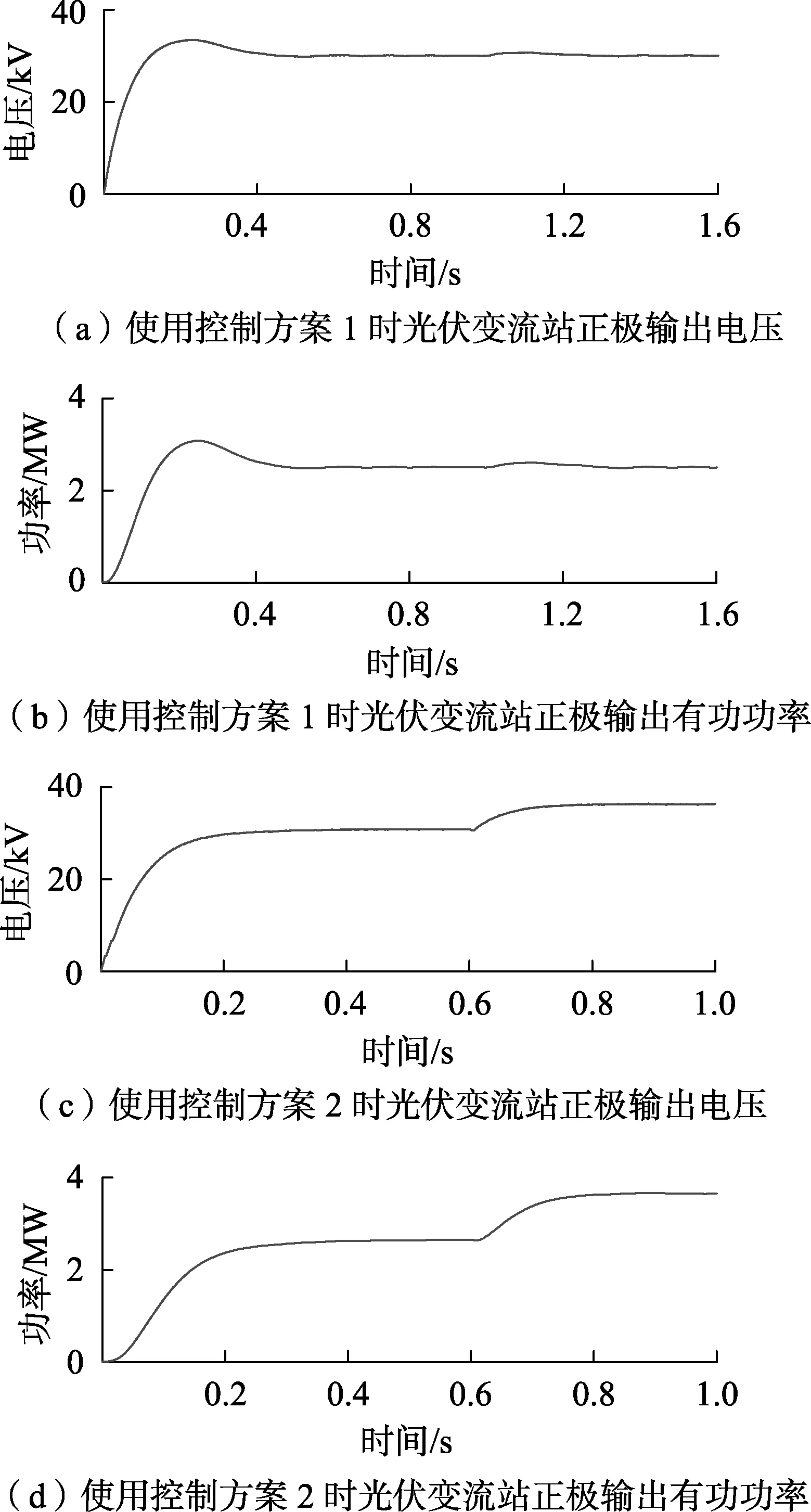
图8 光伏电站孤岛运行的仿真波形Fig.8 Simulative waveforms of photovoltaic station under islanding operation

图8(c)、(d)分别为使用控制方案2时光伏变流站正极输出电压和有功功率波形图。仿真初始时光伏电池投入运行，0.6 s改变光伏电池输入辐照度与温度。由图8(c)、(d)可知，光伏变流站输出电压响应时间约为0.3 s，光伏变流站正极输出稳定电压值约为30.8 kV。0.6 s时改变光伏输入量，光伏变流站输出电压跟踪最大功率点的变化，稳定在新的最大功率点，输出电压约为36.2 kV。

比较方案1与方案2可以看出，当光伏电站处于孤岛模式时，方案1具有抗辐照度及温度扰动的能力，即当光伏输入改变时，可以保证光伏变流站输出电压一定，但光伏电池投入运行时，光伏变流站输出电压超调量较大;方案2可以实现光伏变流站的最大功率控制，且超调较小，响应速度快，但输出电压由最大功率点决定，抗辐照度及温度干扰能力弱。

3.2 并网运行的仿真分析

初始时，光伏电站投入运行并处于孤岛运行状态，MMC各子模块处于闭锁状态。光伏电站输出稳定在±30 kV后解锁MMC，并用交流电网对MMC各子模块电容充电。充电结束后，MMC变流站与光伏电站接入直流电网。调整卸荷电阻阻值，使得光伏变流站输出电压稳定至±30 kV。光伏变流站输出电压稳定后切除卸荷电路。系统稳定运行一段时间后，增大光伏输入辐照度至837.45 MJ/m2，增大光伏输入温度至16.9 ℃，检验控制系统抗光伏输入干扰的能力。

光伏变流站采用控制方案1时，Sc触发信号控制系统中，vmppt的初值为650 V，PI控制器的比例系数为1，积分常数为0.50；S1— S4触发信号控制系统中，PI控制器的比例系数为0.001，积分常数为2。0.6 s 光伏变流站输出电压基本稳定。设置0.59 s解锁MMC，并对各桥臂中的4个子模块充电。0.6 s先将MMC及光伏变流站接入±30 kV直流电网，再切除MMC直流侧充电回路负载。0.72 s切除卸荷电阻，1.5 s改变光伏输入辐照度及温度。系统波形如图9所示。

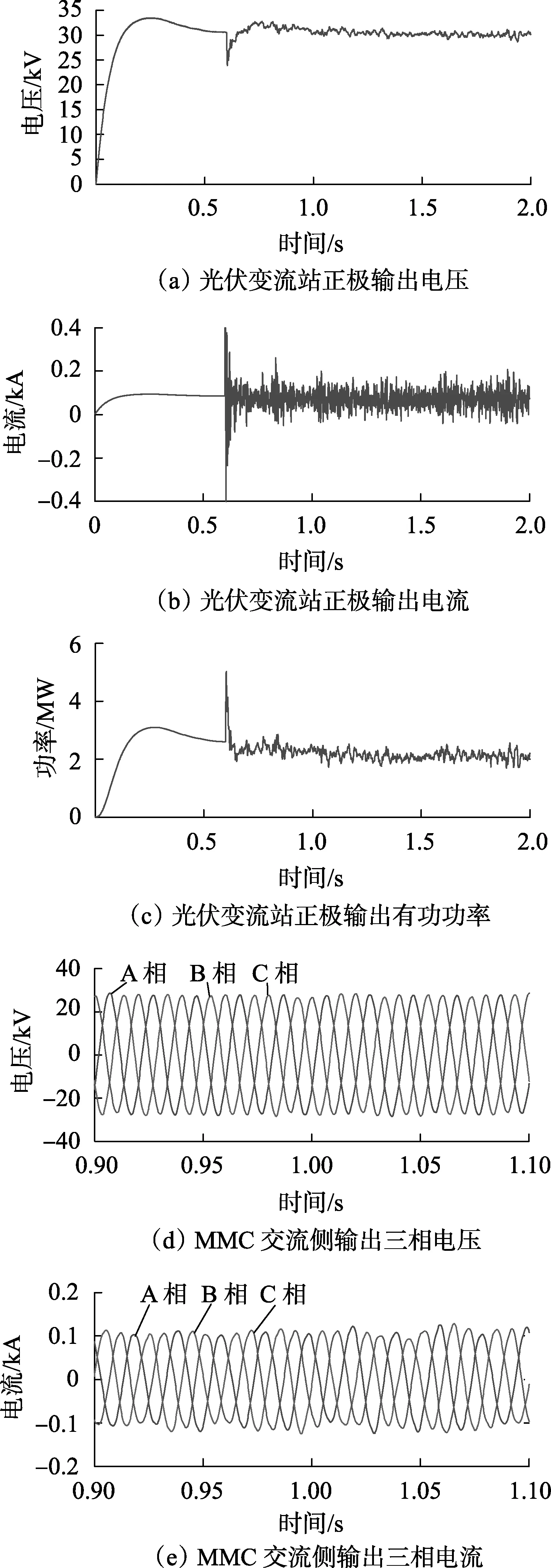
图9 使用控制方案1时光伏并网运行仿真波形Fig.9 Simulative waveforms of grid-connected photovoltaic with control scheme 1

光伏电站接入前，由图9(a)—(c)可以看出，光伏电站投入运行的输出电压响应时间约为0.5 s，单极输出电压峰值约为33 kV，单极输出电压稳定值约为30 kV，电流稳定值约为0.9 kA，光伏电站单极输出有功功率跟随电压变化，稳定值约为2.6 MW。

由图9(a)、(c)可知，光伏电站接入瞬间，其输出电压跌落至约23.8 kV，接入后约0.7 s，其输出电压稳定，单极输出电压约为30 kV，单极输出有功约为2.1 MW。光伏输入改变后约0.15 s，光伏电站输出电压恢复至30 kV，单极输出有功约为2.2 MW。

由于采用定输出电压控制S1—S4，故输出电压波形较为稳定，交流侧电流波形平滑。但改变光伏输入辐照度与温度后，由于电压不变导致输出功率基本不变，即输出功率不随光伏最大功率点变化而变化。

光伏变流站采用控制方案2时，Sc触发信号控制系统中，PI控制器比例系数为1，积分常数为0.50； S1—S4触发信号控制系统中，vmppt初值为650 V，PI控制器的比例系数为1，积分常数为0.5。0.24 s光伏变流站输出电压达到30 kV并基本稳定。设置0.23 s解锁MMC，并对各桥臂中的4个子模块充电。0.24 s先将MMC及光伏变流站接入±30 kV直流电网，再切除MMC直流侧充电回路负载。0.32 s切除卸荷电阻，1 s改变光伏输入辐照度及温度。系统仿真波形如图10所示。光伏电站接入前，由图10(a)—(c)可以看出，光伏电站投入运行的单极输出电压稳定值约为32.57 kV，电流稳定值约为89 A，光伏电站输出有功功率跟随电压变化，稳定值约为3 MW。

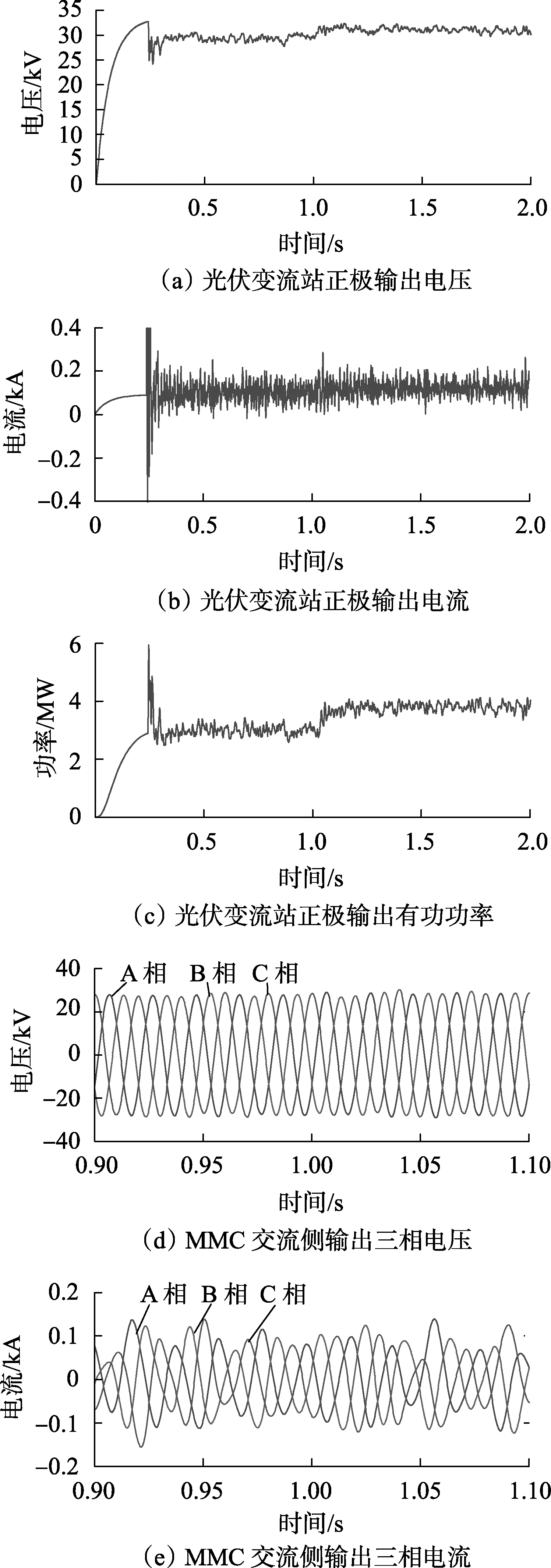
图10 使用控制方案2时光伏并网运行仿真波形Fig.10 Simulative waveforms of grid-connected photovoltaic with control scheme 2

由图10(a)、(c)可知，光伏电站接入瞬间，其输出电压跌落至约24 kV，接入后约0.43 s，光伏变流站输出电压稳定，单极输出电压约为29.4 kV，单极输出有功约为2.85 MW。光伏输入改变后约为0.45 s，光伏电站输出电压恢复稳定，单极输出电压约为30.75 kV， 单极输出有功约为3.76 MW，输出有功功率随着光伏最大功率点的改变而改变。

由于采用最大功率定电压控制S1— S4，故改变光伏输入辐照度与温度后，输出功率跟随光伏最大功率点变化而变化。但光伏输出稳定电压依靠后级变流器控制，交流侧电流波形波动较大。

对比图9(a)、(d)、(e)和图10(a)、(d)、(e)，控制方案1与控制方案2都可以控制光伏变流站输出电压稳定在30 kV，且并网换流器输出交流三相电压约为20 kV、电流约为84.9 A，可以接入交流电网。其中，方案1是通过光伏变流站中定输出电压控制S1—S4实现稳定光伏输出电压的功能；方案2是通过交流并网变流站中作为电流矢量解耦控制外环的定直流侧电压控制，实现稳定光伏输出电压的功能。在控制方案1中，前级光伏变流器与后级并网换流器均采用定直流电压控制；而控制方案2中，只有后级并网换流器采用定直流电压控制。所以相比于控制方案2，控制方案1的并网换流器输出电流更加平滑。

控制方案1与控制方案2的控制效果可以由图9(a)、(c)和图10(a)、(c)的对比得出。当光伏输入改变时，方案1中的直流电压闭环控制作用效果更加明显，直流侧电压更稳定，电压波动受光照扰动的影响较小，但光伏电站送出有功较小且并未工作在最大功率点；方案2中的最大功率定电压控制作用效果更加明显，光伏电站在最大功率点处运行，输出有功较大，且随着光照的变化而变化，但直流电压波动较大，并不适合于对电压要求较高的情况，且电压的稳定控制依赖于后级逆变器。

控制方案1与控制方案2的响应速度可以由图9(a)和图10(a)的对比得出。采用方案1时，光伏接入系统响应速度较慢，抗光照扰动恢复速度较快；采用方案2时，光伏接入系统响应速度较快，抗光照扰动恢复速度较慢。在接入系统瞬间，方案1与方案2电压跌落值基本相同。

针对直流电网中接入直流负荷后的情况，由于光伏最大功率点由辐照度及温度决定，在辐照度与温度不变的情况下，光伏输出功率不变，故直流负荷接入会引起直流电网与交流系统之间的功率传输发生变化，具体与负荷大小及换流站控制方式有关。本文并网换流站控制器外环采用定直流电压与无功功率控制，内环采用电流解耦控制，故无论采用控制方案1还是方案2，直流电网电压基本不变。

具体地，采用控制方案1时，由于光伏电站采用定输出电压控制，故接入直流负荷后，无论辐照度和温度是否改变，光伏电站输出功率变化较小。与无直流负荷相比，直流电网输入交流系统的功率减小；直流负荷大于光伏发电时，交流系统需向直流电网供电。采用控制方案2时，在并网换流站的控制作用下，直流电网电压基本不变，由于光伏电站采用最大功率跟踪控制，光伏输出功率随辐照度或温度变化而变化。直流负荷接入后，交流系统与直流电网之间的功率交互受辐照度、温度及直流负荷大小三方面影响。

特别地，正午时若采用控制方案1，光伏输出功率无显著增加，直流电网与交流系统之间的功率传输与其他时刻接入同等大小直流负荷的情况基本相同，直流电网电压较方案2更为平稳，虽无弃光现象，但光伏利用率较低。若采用控制方案2，则光伏输出功率处于一天中的最大值，此时除向直流负荷供电，还可调整直流电网向交流系统的传输功率防止弃光，光伏利用率较方案1要高。

4 结论

本文在对比光伏直流汇集接入与交流接入方式的基础上，给出了某市光伏直流汇集接入系统的拓扑结构与PSCAD模型。针对BFBIC光伏变流站拓扑结构，给出了2种控制策略。控制方案1采用最大功率定电压控制BFBIC的有源箝位部分，定输出电压控制Boost部分；控制方案2采用定输入电流控制有源箝位部分，最大功率定电压控制Boost部分。为实现光伏最大功率控制，本文采用控制方案2，并通过仿真与控制方案1对比，验证了方案2的可行性。

此外，经仿真分析可知，控制方案1具有较强的抗光照干扰能力，控制方案2具有较强的光伏输出能力。给出控制方案选择建议如下：当光伏系统运行在孤岛状态时，由于控制方案2不能独立控制光伏输出电压稳定，故可考虑采用控制方案1；当光伏系统运行在并网状态时，若可以通过后级逆变器稳定直流电压，且对光伏送出电能的要求高于直流电压稳定的要求，可考虑采用方案2；光伏系统运行在并网状态，若后级逆变器不含稳压环节，或系统对光伏输出直流电压稳定性要求较高，则应考虑使用控制方案1。结合实际情况，亦可考虑采用2种控制策略配合的方式。