提高DFIG低电压穿越性能的转子Crowbar自适应切除控制方法

2018-09-13姜惠兰贾燕琪周照清薛静玮

电力自动化设备 2018年9期

姜惠兰，周陶，贾燕琪，陈娟，张弛，周照清，薛静玮

天津大学智能电网教育部重点实验室，天津 300072)

0 引言

电力电子设备随着其技术的不断发展，在电力系统中得到了越来越多的应用[1]。其中，电力电子变换技术的进步使以风能为代表的清洁能源得以实现利用。双馈风力发电机DFIG(Doubly-Fed Induction Generator)作为主流机型被广泛应用于大型风电场中，风电渗透率的不断提高改变了电力电子化电力系统的运行特性。

DFIG的暂态特性十分复杂，由于其定子直接与电网相连，在系统发生故障时定子磁链无法突变，将在转子绕组上感应出极大的电流，并有可能损坏风机和变流器，或造成风机脱网。因此，风电机组必须拥有满足电网运营商所要求的低电压穿越LVRT(Low Voltage Ride-Through)能力[2- 4]。

目前，大多数的DFIG采用转子侧并联Crowbar保护电路在电网故障期间加快故障电流和定子暂态磁链的衰减，以提高风机的LVRT能力。文献[5-9]从DFIG的数学模型出发，根据Crowbar投入后的短路特性推导了转子电流的暂态表达式。文献[10-12]讨论了Crowbar的不同阻值以及切除时刻对系统产生的影响，其中文献[12]指出Crowbar电阻对风机LVRT性能的影响很大，且由于Crowbar电路投入期间DFIG将近似于异步电动机工作，从电网吸收大量的无功功率，进一步拉低故障点电压，因此Crowbar在切除故障之前被切除能减少DFIG从系统吸收无功，达到更好的LVRT效果。然而过早地切除Crowbar也可能导致转子电流暂态扰动过大并再次投入Crowbar。文献[13-14]给出了Crowbar阻值优化方案，但对Crowbar切除时间并没有深入研究，仍采用Crowbar传统控制策略。

Crowbar传统控制策略在系统故障造成不同电压跌落深度下均使用固定的电流阈值及延时来对Crowbar进行切除，这将带来两方面的问题：当故障较为严重时Crowbar将会多次反复投切，增加了DFIG所吸收的系统无功，不利于系统电压恢复，同时会降低电力电子开关器件的使用寿命，并给DFIG带来电磁转矩冲击[15]，对风机安全造成危害；当故障较轻时，Crowbar的延时切除使得Crowbar的投入时间过长，增大了Crowbar投入期间DFIG所需吸收的系统无功功率，不利于DFIG的LVRT性能。

针对目前Crowbar切除控制策略的不足，本文提出了一种Crowbar自适应切除控制策略，对Crowbar切除后DFIG转子电流暂态变化过程进行了理论推导分析，通过实时计算假设在当前时刻切除Crowbar电路将产生的转子电流最大值来实现对Crowbar切除时刻的有效控制，以保证在Crowbar不会再投入的前提下尽早切除Crowbar，最大限度地降低Crowbar反复投入所带来的不利影响。

1 DFIG的数学模型

在电动机惯例下且变量均折算至定子侧后，DFIG在转子转速参考坐标系下的电压和磁链方程可以表示为：

(1)

其中，上标r表示转子坐标系下的变量；us、ur分别为定、转子电压；ψs、ψr分别为定、转子磁链；is、ir分别为定、转子电流；Rs、Rr分别为定、转子绕组电阻；Ls、Lr、Lm分别为定、转子绕组等效电感及定、转子绕组间的互感；ωr为转子转速。

2 故障时DFIG转子电流骤升机理

假设系统在t0时刻之前稳定运行，t0时刻系统发生三相短路故障，并导致DFIG定子电压跌落且跌落深度为1-h，此时定子电压可表示为：

(2)

其中，Us0为故障发生前的定子电压；ωslip=ωs-ωr为转差转速，ωs为同步转速。

假设t0=0，将式(2)代入式(1)可得电压跌落后的定子磁链表达式[16-17]：

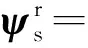
(3)

其中，τs=Ls/Rs为定子时间常数。

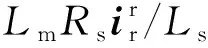
(4)

消去式(1)中的转子磁链和定子电流，整理可得转子电压与转子电流、定子磁链的关系式为：

(5)

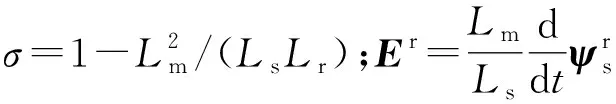
根据式(5)可以得到DFIG等效电路图，如图1所示。

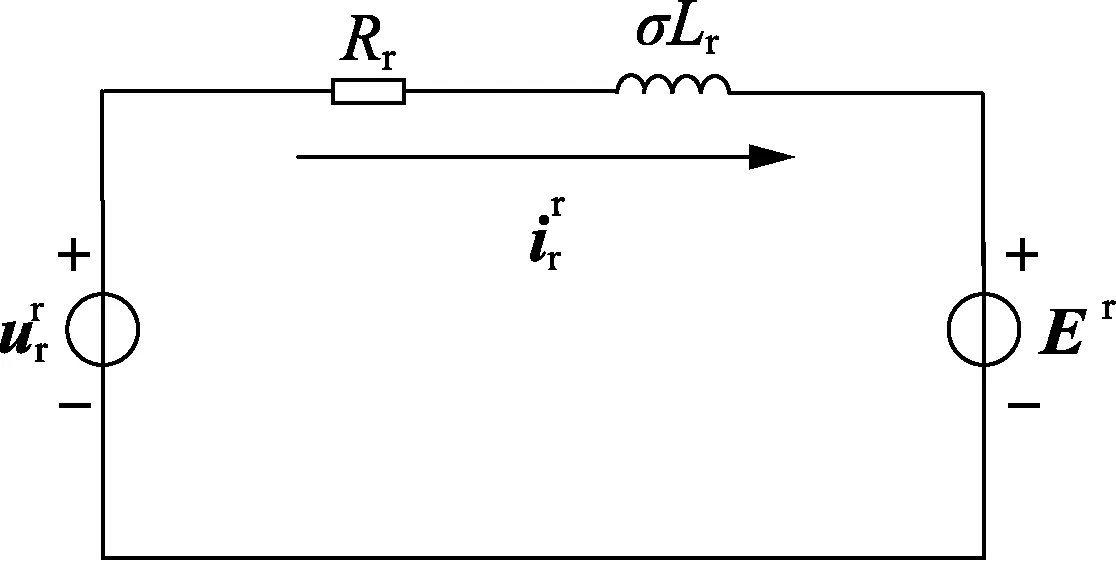
图1 DFIG等效电路图Fig.1 Equivalent model of DFIG

将式(4)代入Er中，可得故障发生后DFIG在转子转速坐标系下定子磁链在转子侧所产生的感应电动势为：

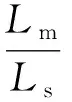
(6)

其中，s=(ωs-ωr)/ωs为转差率。

若忽略较小的1/τs项，则感应电动势Er可表示为[17]：

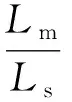
(7)

由式(7)可以看出，由于定、转子磁场耦合，故障发生后定子磁链在转子绕组上所产生的感应电动势分为2个部分：第一项是在转子转速坐标系中以转差转速旋转的交流分量，其幅值分别与转差率和跌落后的定子电压成正比；第二项则是按照τs衰减的直流分量，在转子转速坐标系中以转子转速反向旋转。

然而从式(5)可知，转子电流大小取决于转子电压和感应电动势在转子电阻上产生的压降。由于DFIG的转差率通常在-0.2～0.2之间，并且当电压发生严重跌落时h极小，这意味着定子磁链将在转子绕组上产生较大的感应电动势。若不能采取有效的措施，该暂态感应电动势容易超出RSC的可控电压范围，从而导致转子电流的骤升并在转子绕组上产生过电流，损坏机组和变流器。

3 Crowbar切除后的转子电流暂态分析

设在t1时刻Crowbar电路投入工作，同时闭锁RSC，并在t2时刻切除Crowbar并恢复RSC的工作。Crowbar切除后，转子电压方程和DFIG的等效电路图仍为式(5)和图1，若假设在LVRT过程中DFIG的转速不发生变化[18]，将式(7)代入式(5)中并求解式(5)的转子电流微分方程，即可得到Crowbar切除后的转子电流表达式：

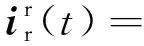
(8)

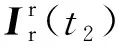
(9)

其中，τr=σLr/Rr为转子时间常数。

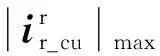
(10)

4 Crowbar自适应切除控制策略

Crowbar的投入时长由电网的故障程度及Crowbar的控制策略共同影响：电网故障越严重则Crowbar的投入时间越长；然而相同故障下Crowbar投入时间的长短主要取决于Crowbar的控制策略。因此调整Crowbar所采取的策略是控制其投入时长的有效手段。

Crowbar的传统控制策略是按照设定的固定阈值来执行[19]，即当转子电流幅值|ir|超过Crowbar动作值Ir_th时投入Crowbar，小于返回值Ir_re时则经过一段延时后切除Crowbar。由式(8)可知，如果采用Crowbar传统控制策略，当电网故障程度较严重时，如果Crowbar的切除延时时间设置得不合理，Crowbar切除仍可能引起过大的转子暂态电流并超过Ir_th，从而造成Crowbar的再次投入；当电压跌落程度较轻时，Crowbar需等到转子电流小于Ir_re并延时一段时间之后才能被切除，导致Crowbar投入的时间远长于其真正所需的时间。所以Crowbar的传统控制策略存在一定不足，诸如降低DFIG的LVRT性能、影响电力电子开关器件的使用寿命、产生DFIG电磁转矩振荡而影响风电机组的安全、增加DFIG从系统吸收的无功功率等。因此，有必要从理论上探求合理的Crowbar切除时间点的有效控制方法。

本文提出了一种Crowbar的自适应切除控制策略，为了在避免Crowbar反复投切的前提下尽早安全切除Crowbar，该策略并不是以转子电流小于固定的Crowbar返回值作为切除Crowbar的判据，而是以按照式(10)所实时计算出的假设当前时刻切除Crowbar将产生的转子电流最大值不会超过Crowbar的动作值Ir_th作为判据的，从而实现对Crowbar切除时刻的有效控制。则当电网发生较为严重的故障时，能够保证Crowbar切除后转子电流不再越限，进而避免其再次投入；电网故障程度较轻时，则能够在保证转子电流不会再对DFIG以及变流器造成威胁的前提下尽早切除Crowbar，从而缩短Crowbar的投入时间。

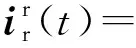
(11)

故障期间Crowbar的控制流程如图2所示。

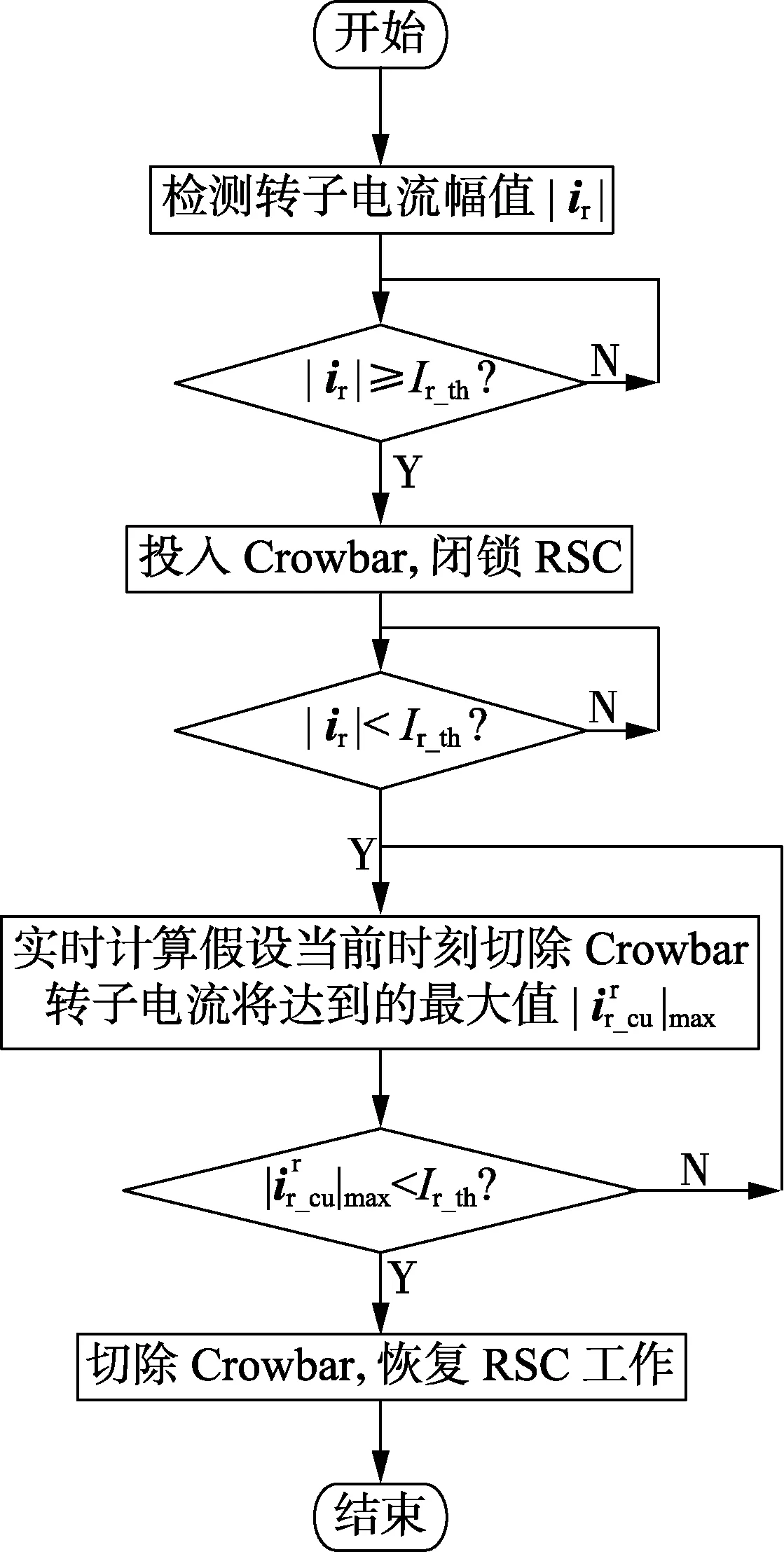
图2 Crowbar自适应控制策略Fig.2 Adaptive control strategy of Crowbar

5 仿真分析

为验证本文所推导的Crowbar切除后转子电流表达式的正确性以及所提出的Crowbar自适应切除控制策略的有效性，下文进行了仿真分析。

在MATLAB/Simulink中搭建如图3所示的1.5 MW DFIG-无穷大系统模型，DFIG参数如下：额定功率为1.5 MW，额定电压为0.575 kV，定子电阻为0.023 p.u.，转子电阻为0.016 p.u.，定子漏感为0.18 p.u.，转子漏感为0.16 p.u.，互感为2.9 p.u.，初始转差率为 -0.2，电容电压为1 150 V，匝间比为0.3。30 km线路参数为：正序、零序电阻分别为0.115 3 Ω/km、0.413 Ω/km；正序、零序电感分别为1.05×10-3H/km、3.32×10-3H/km；正序、零序电容分别为1.133× 10-8F/km、5.01×10-9F/km。

图3 DFIG-无穷大系统模型Fig.3 Model of DFIG-infinite system

假设在0.05 s时系统发生三相短路故障，导致定子电压跌落深度分别为60%和80%，在0.25 s切除故障，故障持续200 ms，Crowbar电阻取0.1。Crowbar电路的传统控制策略中，转子电流超过Crowbar动作值Ir_th=2 p.u. 时Crowbar投入，小于返回值Ir_re=1.5 p.u.并延时一个同步周期后切除Crowbar。

5.1 Crowbar切除后转子电流表达式验证

为了验证所推导的Crowbar切除后转子电流表达式的正确性，以便由此计算转子电流最大值，采用Crowbar传统控制策略分别对60%和80%电压跌落深度下的故障情况进行了仿真。为了方便观察Crowbar切除后的转子电流将出现的最大值，仿真过程只进行第一次的转子Crowbar投入与切除。

图4为按照式(11)得到的转子电流计算结果与仿真结果的对比(转子电流为标幺值，后同)，图中实线为仿真结果，虚线为计算结果。可以看出，由式(11)所得到的计算结果曲线与仿真结果曲线基本吻合，说明推导的表达式能够准确反映Crowbar切除后转子电流的暂态过程。

图4 转子电流计算结果与仿真结果对比Fig.4 Comparison between calculative and simulative results of rotor current

由图4可知，电压跌落深度为60%时，Crowbar切除于0.078 9 s，转子电流最大值出现于0.089 5 s，其值为1.772 p.u.，由式(10)得到的计算结果为1.829 p.u.；当跌落深度为80% 时，Crowbar在0.079 2 s切除，转子电流在0.090 1 s出现最大值2.097 p.u.，由式(10)计算的结果为2.11 p.u.。可以看出，由式(10)计算的假设Crowbar切除后转子电流将出现的最大值与仿真结果基本吻合，验证了式(10)的正确性，为寻找Crowbar切除时刻的有效控制提供了前提保证。

5.2 LVRT方案比较

为了体现本文所提的Crowbar自适应切除控制策略的优势，分别采用Crowbar传统控制策略和本文所提策略对定子电压跌落深度为60%和80%的故障进行了仿真，仿真结果如图5和图6所示。图中，实线代表Crowbar传统控制策略，虚线代表本文所提出的控制策略。

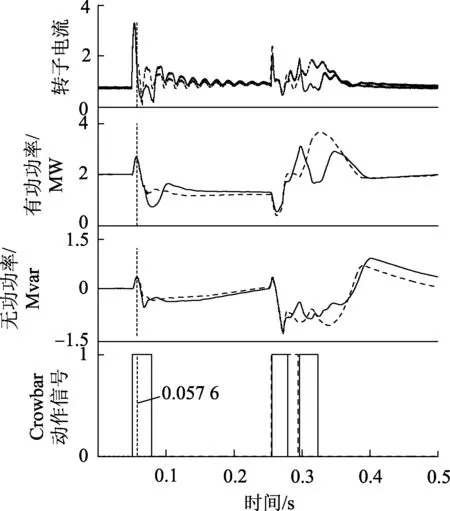
图5 跌落深度为60%时的LVRT方案效果对比Fig.5 Comparison between two LVRT strategies under 60% voltage dip

图6 跌落深度为80%时的LVRT方案效果对比Fig.6 Comparison between two LVRT strategies under 80% voltage dip

从图5可知，当电压跌落深度为60%时，Crowbar于0.050 6 s投入；采用传统控制策略时，Crowbar于0.078 9 s切除，采用本文所提策略时则于0.057 6 s切除，相对提早了21.3 ms。这是由于采用传统控制策略时，当转子电流已经被抑制后Crowbar没有及时切除，增加了DFIG作为异步电动机投入且吸收系统无功的时间；而本文提出的自适应切除策略能够实现Crowbar尽早切除，使Crowbar动作持续时间尽可能缩短，从而减少了DFIG从系统吸收的无功功率。

由图6可知，当电压跌落深度为80%时，Crowbar于0.050 6 s投入；采用传统控制策略时，Crowbar于0.079 2 s第1次切除，于0.088 6 s再次投入，于0.106 0 s最终切除；而采用本文所提自适应策略时，Crowbar则于0.090 8 s一次性切除。通过分析可以看出，采用传统控制策略导致故障发生后Crowbar反复投切了2次，故障期间总的投入时间为46 ms；本文所提方案下Crowbar投入时间缩短了5.8 ms，且在整个故障期间只投入1次，不仅减少了故障期间DFIG作为异步机运行从系统吸收的无功，还有效降低了对风机及其控制装置安全的影响。