考虑移动充电车路径选择和能源补给的充电服务一体化经济调度

2018-09-13戚博硕韩震焘葛少云

电力自动化设备 2018年9期

刘洪,戚博硕，韩震焘，葛少云，张强

1. 天津大学智能电网教育部重点实验室，天津 300072；2. 国网辽宁省电力有限公司经济技术研究院，辽宁沈阳110013)

0 引言

电动汽车作为新型的交通工具，可以有效缓解能源和环境压力[1]，因而得到国家的大力推广。作为电动汽车运行的重要支撑，完善的电动汽车充电服务体系可以促进电动汽车的规模化应用。目前，私人电动汽车主要选择在充电站或居民小区进行电能补给。但受到城市土地资源短缺、现阶段充电站难以盈利[2]等客观因素影响，充电站的建设数量远低于社会预期，电动汽车在行驶途中很难找到合适的充电站进行充电。而部分居民小区现有配电网容量有限、电力负荷紧张，不能接纳过多电动汽车[3-5]。与此同时，共享经济已渐成规模：在国内，共享燃油汽车现身北京、成都等地，共享电动汽车正在酝酿中；在国外，Car2Go公司已在美国圣迭戈推出共享电动车项目，但由于当地充电设施短缺，共享电动车运营同样陷入困境[6]。因此，亟待探索新的充电服务模式，用于解决电动汽车充电难的问题。

无线充电可以作为一种候选充电服务模式，如韩国科学技术学院将充电电缆埋在路面下方的联网电动车OHV(Online Electric Vehicle)项目[7]，但和充电站建设类似，高昂的建设费用使得该模式在短时间内难以普及。文献[8]提出移动充电服务的概念，并分析了在物联网技术支持下移动充电服务的技术可行性；同时指出移动充电服务可以提高充电设施利用率，有助于充电行为在时间上交错进行，避免电动汽车无序充电冲击电网。文献[9]中认为移动充电服务模式可以解决现阶段充电设施覆盖率不足的问题，并研究了移动充电车容量的经济配置。

移动充电服务运营过程中主要涉及移动充电车的路径选择和能源补给两过程。在车辆路径选择方面，文献[10]研究了移动充电车在接到充电服务请求后在路网中的调度策略，但并未涉及移动充电车的能源补给策略；文献[11]考虑加权道路长度，建立了充换电服务网络中配送车辆路径选择模型，文献[12]建立了动态路网中单车场、多车辆带时间窗的车辆路径模型，并设计相应算法进行求解，但文献[11-12]未涉及多个车场的车辆路径问题；文献[13-14]针对多车场、多车辆带时间窗的车辆路径问题，给出“先客户聚类再规划路径”的两阶段算法，这种方法虽然求解速度较快，但解的质量不高。上述研究均是基于静态路网的假设且车辆不能重复使用。在移动充电车能源补给领域，由于移动充电车车辆类型易于统一，换电模式可作为移动充电车有效的能源补给方式，文献[15]以充换电站各时刻的充电功率作为决策变量，建立多目标调度模型，得出次日优化充电计划；文献[16]考虑公交车的运行规律和耗电特性，建立了以充电成本最小为目标的两阶段充电模型。但上述文献中均假设电池的在充电过程中完全可控，未深入考虑电池荷电状态(SOC)、电池数量和充电机数量间的匹配关系，所得最优解通常难以实现[17]。另外，目前尚未有相关文献研究如何将两者结合实现一体化优化。

为此，本文提出了包含移动充电车行驶路径选择和能源补给的移动充电服务一体化经济调度模型。分析了移动充电服务运营模式与优化调度框架；针对移动充电车行驶路径选择过程，考虑用户服务时间窗和动态路网，构建了移动充电车可重复使用的路径选择模型，通过优化用户的服务顺序和行驶路段使得物流成本最小；针对移动充电车能源补给过程，考虑离散化的电池组荷电状态，构建了考虑分时电价的有序充电整数规划模型，在满足移动充电车换电需求的前提下，通过优化不同荷电状态电池组的接入时段使得充电费用最小；以移动充电车为纽带，构建了包含能源服务站-移动充电车-用户的一体化经济调度模型并设计算法实现用户智能分配，对模型进行求解；通过算例分析验证了模型和算法的有效性。所建模型及仿真结果可以为移动充电服务运营商在移动充电车路径选择和能源补给两方面提供有价值的参考，有助于运营商控制日运营成本，提高经济效益。

1 移动充电服务运营模式及优化调度框架

设置多个能源服务站可以降低物流成本、提高服务效率[14]。移动充电服务运营模式如附录中图A1所示。各能源服务站调度移动充电车从而有序地为用户充电，当移动充电车内电池组剩余电量不足时，车辆返回各自能源服务站更换电池组，之后继续服务用户。能源服务站可对卸载的电池组进行充电、维护。

对于路径选择过程，在满足用户需求和每条子路径中移动充电车容量约束的前提下，保证服务质量、降低物流成本是运营商追求的目标；对于电池组能源补给过程，在满足移动充电车换电需求的前提下，运营商期望降低充电成本。显然，不同的路径选择方案会产生不同的换电需求，而未考虑换电能力得到的路径选择方案往往是不可行的，因此，需要从整体角度协调两过程，避免决策冲突，得到全局最优解。

考虑将两者结合的移动充电服务运营优化调度框架如附录中图A2所示。运营商首先为各个能源服务站动态安排所需服务的用户，为每辆移动充电车制定路径方案，得到物流费用；随后，根据路径方案制定充电计划，并将充电费用反馈回该路径方案上。运营商根据该一体化调度方案的总费用，重新调整路径方案，并重新制定充电计划，如此循环迭代至预先设定的最大迭代次数，得到优化结果，实现移动充电服务运营的一体化调度。

2 移动充电车行驶路径调度模型

2.1 动态路网模型

定义动态路网模型为G={V,E,fij(t)}，其中V={v1,v2,…,vn}表示路网节点的集合，E={e1,e2,…,em}表示路网中路段集合，fij(t)表示对每一个路段(vi,vj)∈E的时间代价函数，t∈[t0,tm]为车辆离开vi的时间，[t0,tm]为问题研究的时间域。

因为人们日常出行规律具有周期性，所以车辆在路段中的行程时间也呈现一定周期性。选用Ichoua等[18]提出的旅行速度分段依赖函数，该函数通过路段长度和行驶速度作比计算行程时间，所得行程时间连续变化，满足先进先出准则，具体如附录中图A3所示。

用T={T0,T1,…,TL}表示时段集合，[Tl-1,Tl]为第l个时段，时段间隔长度记为ΔT，Vij(t)表示t时刻在路段(vi,vj)上的行驶速度，可采用式(1)计算车辆在路段(vi,vj)上的行程时间。

(1)

其中，Tvi,vj(di,t)为t时刻在路段(vi,vj)上已经行驶了距离di的车辆继续行驶完全程所需的时间；tre为t时刻所在时段的剩余时间，即tre=Tl-t且t∈[Tl-1,Tl)；dij为路段(vi,vj)的长度；dre=treVij(t)，为以t时刻的恒定速度驶完当前时段对应的行驶里程。

2.2 考虑车辆重复使用的移动充电车路径选择模型

构建移动充电车路径选择模型前，本文进行如下假设：在为移动充电车安排行驶路径之前已知每个用户的地理位置、充电需求量、任意用户可接受充电服务的时间窗；每个用户只能由一辆移动充电车服务一次；每辆移动充电车以恒定功率为用户提供充电服务；移动充电车仅在能源服务站和用户所在节点停留，在其他路网节点不停留。

基于上述假设，以移动充电车行驶过程中物流费用最小建立目标函数如下：

(2)

涉及的约束条件如下。

a. 路径约束。

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

b. 移动充电车容量约束。

(12)

其中，Qk为移动充电车k的容量，且Qk=NnumCr(∀k∈K)，Nnum为移动充电车搭载电池组的额定数量，Cr为每块电池组的可用容量。式(12)表示每条子路径上用户电量需求总和不超过移动充电车最大容量限制。

c. 能源服务站物流能力约束。

(13)

其中，|Kd|为能源服务站d含移动充电车数量。式(13)表示各能源服务站调用移动充电车的数量不超过该能源服务站拥有的车辆数量。

d. 用户时间窗约束。

(14)

(15)

3 电池组有序充电的整数规划模型

为方便对移动充电车换电服务模型进行分析，将全天24 h以Δh(单位为min)间隔等分，分成H个调度时段，H=24×60/Δh。对模型做出如下假设：① 第t个时段更换下来的电池组最早可在第t+1个时段起始时刻开始充电；② 充电机和电池组采用一对一的恒功率充电方式，出于对电池组寿命的考虑，电池组接入充电机后直至电量到达预设值时方可被换下；③ 移动充电车内车载电池通过串并联形式组成，通过电池管理系统对电池组内电池放电进行控制，因此，可认为移动充电车返回能源服务站换电时各电池组荷电状态值相同。

3.1 电池组荷电状态离散化

在单位时间步长充电机功率已知的情况下，可将电池按充电所需时段数分为Z1类：

(16)

其中，SOCmax为电池组最大荷电状态；SOCmin为电池组最小荷电状态；pc为充电机的额定充电功率；ηc为充电机充电效率；Cr为电池组额定容量；Δh为单位时间步长；「·⎤表示向上取整。

对于第t个时段回收的第n块电池组，其充电时段数Mt,n为：

(17)

通过计算各个时段回收电池组所需充电时段数，可近似得到各电池组充电时长。

3.2 能源服务站内运营建模

对于任意第t个时段，站内电池组按状态可划分为[19]：可用电池组S(t)，即第t个时段满电电池组；待充电池组NW(t)，即在第t个时段之前未接入充电的电池组；在充电池组NA(t)，即第t个时段处于充电状态的电池组。

将新入站电池组荷电状态进行离散化后，得到规模为Z×H的二维矩阵Ω，如式(18)所示。

(18)

其中，Ωz,h为第h个充电调度时段回收充电时长为z的电池组数量。

能源服务站内各状态电池组间的转移关系可表示为：

S(t)=S(t-1)+NC(t)-Nde(t)

(19)

NW(t)=NW(t-1)-NI(t-1)+Nnew(t)

(20)

NA(t)=NA(t-1)-NC(t)+NI(t)

(21)

(22)

(23)

(24)

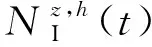
3.3 单个能源服务站充电优化模型建立

区域内各能源服务站运营情况相同，单个能源服务站内以充电费用最小为目标，模型如下：

(25)

其中，NCH为该能源服务站内充电机数；X(ic,t)为第ic个充电机在第t个时段的状态，X(ic,t)=1表示充电机处于充电状态，X(ic,t)=0表示充电机处于其他状态；pr(t)为第t个时段的电价。

涉及的约束条件如下。

a. 充电设施约束。能源服务站内任意时段在充电池组数量不能超过站内充电机数量。

NA(t)≤NCH

(26)

b. 待充电池约束。能源服务站内任意时刻在接入电池组数量不能超过该类电池该时刻的电池组数量。

(27)

c. 能源服务站换电能力约束。为使移动充电服务正常进行，第t个时段站内满电电池组数量不小于此时移动充电车的换电需求。

S(t)≥Nde(t)

(28)

d. 接入时段约束。因电池充电为持续充电过程，为避免对下一调度周期产生影响，充电负荷不应持续到下一调度时段。则第z类电池允许接入时段为：

t∈[1,H-z]

(29)

4 移动充电服务一体化经济调度模型

4.1 两过程的关联方程

移动充电车为用户服务充电的过程与能源服务站内电池组有序充电的过程，体现了移动充电车的载体特性，这期间产生电能的转移。能源服务站内电池组的优化过程与移动充电车路径选择方案密切相关。

k1(t)辆移动充电车在第t个时段从能源服务站出发，换电需求如式(30)所示。

Nde(t)=Nnumk1(t)k1(t)∈Kd

(30)

k2(t)辆移动充电车在第t个时段返回能源服务站，将新入站电池组荷电状态离散化，更新式(18)；根据假设 ①，时段t回收电池组数量影响时段t+1待充电池数量，得到式(31)。

Nnew(t+1)=Nnumk2(t)k2(t)∈Kd

(31)

将移动充电车离开时刻和返回时刻与Δh作比，并向上取整可以得到其所处时段。

4.2 一体化经济调度模型

从运营商角度出发，移动充电服务日运营费用主要包括移动充电车物流费用和电池组充电费用。根据路径方案制定的充电方案，通过影响日运营费用对移动充电车路径方案产生影响，由此体现移动充电车路径选择与电池组充电优化间的关系。据此建立移动充电服务一体化经济调度模型，目标函数如式(32)所示。

(32)

其中,Ni,CH为第i个能源服务站内充电机数量。涉及的约束条件为式(3)—(15)、式(26)—(31)。

5 遗传算法嵌套lpsolve工具箱的求解方法

车辆路径问题已被证明是一个非确定性多项式难(NP-hard)问题，遗传算法可以对其进行有效求解[20]，因此选择遗传算法求解路径方案；对于电池组有序充电模型，为加快求解速度，采用lpsolve工具箱进行求解。

5.1 染色体编码和用户智能分配

本文采用自然数编码，一组用户排列表示用户服务顺序。借鉴文献[21]在解决多配送中心问题时提出的整体法思想，从寻找全局最优解的角度出发，通过设置虚拟用户实现能源服务站的服务用户的智能分配。以10用户-3能源中心为例，通过设置2个虚拟用户形成12个代码。虚拟用户随机将实际用户分割为3个部分，对应3个能源补给站，如图1所示。为实现有效分割，规定虚拟用户不能相邻，且不能位于代码的首位和末位。

图1 染色体编码示例
Fig.1 Example of chromosome encoding

5.2 适应度函数计算

在得到路径方案后，根据移动充电车出发时刻，更新换电需求，如式(30)所示；根据移动充电车返回时刻，更新下一调度时段待充电池状态，如式(31)所示，并调用lpsolve工具箱求出对应的有序充电方案。

由于构造路径时可能不满足移动充电车车辆数目约束和时间窗约束，将物流费用最小化目标函数松弛为：

(33)

其中，β1和β2为惩罚因子，分别表示方案在用户i延迟服务的惩罚以及总的车辆违反惩罚。

由于能源站内备用电池数量限制，无法满足部分路径方案对应的换电需求，此时将充电费用赋值为一个较大的正数π，则充电费用为：

(34)

5.3 求解流程

本文所提求解方法的整体求解流程图如附录中图A4所示，具体求解步骤如下。

a. 算法初始化。输入路网中速度依赖函数、路网节点坐标、用户的地理位置、时间窗、需求电量、能源服务站内充电机数量、备用电池数量等参数，设置算法相关参数，生成初始种群。

b. 解码染色体形成移动充电车调度方案，计算物流费用；调用lpsolve工具箱得到此路径方案下的最优充电费用，通过5.2节的方法评价其适应度函数。

c. 使用遗传算法更新种群状态。

d. 循环操作。返回步骤b循环计算，直到全局最优解没有更新或者达到种群最大迭代次数，停止循环。

e. 输出最终解，得到移动充电车路径方案及对应的充电方案。

6 算例分析

6.1 算例介绍

图2 区域路网结构示意图Fig.2 Schematic diagram of area road network

区域内环形城市快速路将区域分为3个部分，一般城市中心较为拥堵，郊区附近较为通畅，仿照北京市二环、三环的概念，设置三环之外、二环之外、二环之内区域拥堵系数ξ分别为1、1.5、2。不同道路类型其设计行驶速度也不同，据此设计城市快速路、城市主干路道路类型系数φ分别为1、0.8。参考文献[22]中已有的一些数据，以15 min为一个取样周期，得到基准旅行速度分段时间依赖函数如图3所示。

图3 基准旅行速度分段时间依赖函数Fig.3 Benchmark split time-dependent function of travel speed

综合路况因素和道路类型因素可得到具体路段的时间依赖函数为：

(35)

其中，Vi,j(t)为路段(vi,vj)的速度时间依赖函数；Vbase(t)为基准速度时间依赖函数；ξi,j为路段(vi,vj)所在区域的拥堵系数；φi,j为路段(vi,vj)道路类型系数。

6.2 结果分析

为说明本文所提用户智能分配方法以及一体化求解移动充电服务两过程给运营商带来的经济效益，本文设计了3个仿真案例：案例1首先将用户智能分配到能源服务站，然后进行一体化求解；案例2首先将用户按距离分配到能源服务站，然后进行一体化求解；案例3采用分步优化，首先得到最优路径选择方案，然后在该路径方案下进行电池组充电过程优化。

6.2.1 案例1与案例2经济调度结果分析

表1、表2分别为案例1、2的路径选择方案，表3为相应的物流费用和充电费用。案例1对应的能源服务站电池接入安排见附录C，其中数字0表示能源服务站。通过对比可知，案例1中运营商的总运营成本为620.30元，案例2中运营商的总运营成本为694.96元，案例2与案例1相比运营成本增加了12.04%。

案例1、2中充电成本差异较大，分析2种用户分配策略下各能源服务站的服务用户总需求见图4。可见在两能源服务站参数相同的情况下，案例1中两能源服务站覆盖的用户充电需求分配较为均匀。

表1 案例1路径选择方案Table 1 Routing scheme in Case 1

表2 案例2路径选择方案Table 2 Routing scheme in Case 2

表3 案例1和案例2对应的物流费用和充电费用Table 3 Logistics cost and charging cost of Case 1 and Case 2

图4 各能源服务站服务用户总电量Fig.4 Total power of users served by energy service stations

案例1、2中各能源服务站充电曲线分别如图5和图6所示。从图5可以看出，案例1中，为满足移动充电车换电需求，两能源服务站均在非谷电价时段接入电池。结合附录C中能源服务站接入电池状态，两能源服务站均选择充电时长最短的电池组接入充电，以减少充电费用，这从侧面说明了本文充电优化方法的有效性。从图6可以看出，案例2中，能源服务站1#内备用电池可以满足移动充电车换电需求，且存在闲置，移动充电车所换下的电池全部在夜间低谷时段进行充电；能源服务站2#服务用户需求较多，需多次往返能源服务站进行能源补给。为满足移动充电车需求，能源服务站2#在电价峰时、平时接入较多电池组充电，造成充电费用高昂，增加了运营成本。

图5 案例1中各能源服务站内电池充电状态Fig.5 Battery charging status of energy service station in Case 1

图6 案例2中各能源服务站内电池充电状态Fig.6 Battery charging status of energy service stations in Case 2

通过上述分析可知，案例1中区域内资源利用更加合理。通过本文方法可为能源服务站合理分配用户，降低移动充电车使用频次，减少峰、平时段充电电池组数量，降低整体运营费用。

6.2.2 案例1与案例3运营费用对比

案例3中，采用分步优化得到运营商物流费用和充电费用，案例1和案例3的各项成本如表4所示。虽然方案3所需物流成本较小，但案例1中总运营成本更低，比案例3节省了4.18%，这说明采用分步求解方法往往只能得到问题的次优解，本文在算法中以总运营费用对解的质量进行评价，反复迭代求解，所得结果更优。

表4 案例1和案例3运营费用对比Table 4 Comparison of operating cost between Case 1 and Case 3

6.2.3 不同充电模式运营费用对比

为进一步说明本文所提充电方法的有效性，在已知案例1路径方案的前提下，能源服务站2#采用直接充电策略，得充电曲线如图7所示。由图7可知，使用本文方法优化充电后，能源服务站内电价谷时段充电容量利用率为75.78%，充电费用为230.54元；而采用直接充电策略，电价谷时段充电容量利用率为8.20%，充电费用为620.57元。可见，本文所提方法可充分利用谷时电价时段对空载电池进行充电，大幅降低移动充电服务运营过程中的充电费用。