基于随机矩阵理论的电子式互感器误差状态相关性分析方法

胡 琛,张 竹，焦 洋，李红斌，陈 刚

1. 华中科技大学 强电磁工程与新技术国家重点实验室，湖北 武汉 430074；2. 国网江苏省电力公司电力科学研究院，江苏 南京 211103)

0 引言

电子式互感器作为智能变电站中一次系统和二次系统之间的联络器，从根本上解决了电磁式电流互感器二次信号传输附加误差的问题。然而，现场运行问题中，电子式互感器的准确度问题占据了较大比例[1-2]。空心线圈电流互感器是电子式互感器的一种，其输出信号较弱，而自身又包含大量的电子元器件，极易受到周围环境参量的影响[3]，产生信号波动，引起误差状态发生改变。由于实验室内、现场离线运行以及在线运行空心线圈电流互感器的误差并不一致，互感器误差状态的稳定性较差[4]。国内外针对环境参量作用下空心线圈电流互感器误差变化的机理取得了一定的研究成果。近年来，研究的热点从实验室研究转为在变电站现场建立空心线圈电流互感器在线监测系统[5]，从而更加深入地研究现场运行过程中空心线圈电流互感器的误差特性在周围环境参量下的变化特性，以指导空心线圈电流互感器的设计、工艺及生产。虽然在线监测系统已经积累了大量电子式互感器运行过程中的误差数据和环境参量数据，但是还未充分利用这些数据挖掘在运电子式互感器误差与环境参量之间的内在联系。为此，还需要建立电子式互感器误差状态相关性分析方法，评估电子式互感器误差和环境参量的相关程度。

相关性分析方法可以分为基于模型的分析方法和基于数据驱动的分析方法。基于模型的分析方法的思路为建立各个影响量对电子式互感器作用的机理模型，基于此模型分析误差与影响量之间的相关性[6-7]。然而，基于模型的分析方法高度依赖模型的准确性和可靠性，同时各种假设和前提条件将会影响评估结果的准确性。在运电子式互感器的误差状态受到如温度、湿度、振动、电场、磁场等多种影响量的交叉作用[6]，这些影响量以直接或间接的方式影响着电子式互感器的运行状态，彼此之间又存在耦合关系，所以基于模型的分析方法存在局限性。

基于数据驱动的分析方法不依赖机理模型的准确度，其思路是通过对现场运行数据进行挖掘、处理和分析，探索电子式互感器误差状态和影响量之间的相关性。基于数据驱动的方法包括统计学方法[8-9]、关联规则分析法[10]以及灰色关联分析法[11]。统计学方法通过求解相关系数来评估误差与影响量之间的密切程度。相关系数的计算方法包括皮尔逊(Pearson)简单相关系数、斯皮尔曼(Spearman)等级相关系数以及肯德尔(Kendall)秩相关系数等。当样本容量较少时，相关系数容易出现波动的现象；当样本容量较多时，相关系数的绝对值容易偏小。关联规则分析法基于最小支持度和最小置信度指标，通过迭代识别支持度大于最小支持度的项目集合，提取出置信度不小于最小置信度的项目集合，描述事件之间同时出现的规律和模式。灰色关联分析法是根据误差序列曲线以及影响量序列曲线形状的相似度评价相关程度，曲线同步变化的程度越高，相关性越大。上述相关性分析方法在处理大样本数据时常常表现不佳，且无法应用于实时分析，难以满足电子式互感器误差状态与影响量相关性分析的要求。

随机矩阵理论起源于量子物理学，1951年物理学家Eugene Wigner证明了Wigner矩阵的谱分布满足半圆律，用随机矩阵理论描述带有随机哈密顿量的量子统计系统。随后Dyson、Marchenko以及Pustur都对此进行了深入研究[12-14]。随着随机矩阵理论的成熟，它在无线电、金融、生物等领域都得到了广泛应用。近年来，随机矩阵理论作为一种大数据分析手段，在电力行业也得到了充分重视，成功应用于输变电设备关键性能评估、电网状态识别和异常数据检测[15-17]。

本文基于高维随机矩阵理论，提出了一种电子式互感器误差状态与影响量相关性分析方法，建立了相关性评价指标，利用滑动时间窗实时获取误差状态与影响量的关联关系。

1 随机矩阵理论

随机矩阵是指矩阵中至少有1个元素为随机变量。假设随机矩阵W=(xij)n×n可以分解为W=CYV，其中，C和V为n阶Haar酉矩阵；Y为对角阵，其对角线元素是W的奇异值。当满足一定的条件时，W的极限谱分布由其奇异值的概率测度唯一确定，且特征值在复平面上收敛到圆环，圆环的内外半径为：

(1)

其中，v为矩阵W的奇异值的概率测度。上述即为单环定理[18]。

当矩阵W=(xij)∈Cm×n为非Hermitian矩阵，其元素为独立同分布的随机变量，且矩阵W的行向量满足均值为0、方差为1的条件。对于多个矩阵Wi，定义矩阵乘积Z为：

(2)

其中，Wui∈Cm×m为Wi的奇异值等价矩阵；L为矩阵数量。将矩阵Z标准化为Zstd，使其满足σ2(zi)=1/n(其中zi=(zi1，zi2，…，zin)为矩阵Z的行向量)，则Zstd的极限谱分布以概率1收敛，其概率密度函数如式(3)所示。

(3)

其中，c=m/n∈(0，1]，m、n→∞；λz为特征值。Zstd的特征值分布于复平面中一个圆环内，其内环的半径为(1-c)L /2，外环的半径为1。由于单环定理可以表征大量甚至海量数据环境下的概率分布，本文利用单环定理对电子式互感器误差状态与影响量的相关性进行研究。

2 相关性分析方法

2.1 分析方法

为了研究电子式互感器误差状态与影响量之间的内在联系，首先需要获取电子式互感器误差状态数据以及影响量监测数据，将其作为高维随机矩阵的输入。然后基于随机矩阵理论，分析所构建的随机矩阵是否满足单环定理，来评估电子式互感器的误差状态的相关性。虽然高维随机矩阵的建立需要满足维数趋于无穷的理论条件，但是当矩阵规模为几十到几百维时也能得到较为准确的收敛结果。

假设电子式互感器在运行过程中，误差影响量数据有M类，分别为{P1，P2，…，PM}，误差数据有N类，分别记为{Q1，Q2，…，QN}。在评估时间窗内，进行了T次测量，所有误差影响因素的监测数据可以构成一个误差影响量矩阵D1：

(4)

其中，元素Pij为第i个可测状态参量在j时刻的测量值。当M和T充分大，并且M和T在同一数量级时，矩阵D1可以视为一个高维随机矩阵。

同样地，在评估时间窗内，误差状态数据也可以构成一个如式(5)所示的误差状态矩阵D2，该矩阵也可视为一个高维随机矩阵。

(5)

由于高维随机矩阵允许元素具有不同的单位和数量级，故可直接将矩阵D1和矩阵D2合并，构建影响量相关性评估矩阵D。

(6)

按式(7)对评估矩阵D中的元素进行标准化处理：

(7)

其中，xi=(xi1，xi2，…，xiT)。标准化后的矩阵D3=(yij)(M+N)×T中元素的平均值和方差满足：

(8)

其中，yi=(yi1，yi2,…,yiT)T,1≤i≤M+N。矩阵D3为标准非Hermitian矩阵，它的奇异值等价矩阵如式(9)所示。

(9)

其中，U为Haar酉矩阵。对于L个任意的标准非Hermitian矩阵D3，可以求出L个奇异值等价矩阵，为了简化分析，一般情况下可以取L=1，矩阵积可以表示为：

(10)

(11)

(12)

图1 相关性分析数据处理方法流程图Fig.1 Flowchart of data processing method for correlation analysis

电子式互感器的误差状态数据包括比差和角差，误差影响量包括非电气影响量和电气影响量，其中电气影响量包括电场、磁场、负荷等因素，非电气影响量包括温度、湿度、振动等因素。尽管评估矩阵D中的元素含有不同的单位和数量级，但是经过数据标准化运算后，可以将元素的数量级进行归一化处理。

2.2 矩阵扩展方法

由于电子式互感器的误差数据和误差影响量数据的类型较少，即使将两者组合后，所构建的随机矩阵的维数依然较少。为了解决这一问题，需要在稀疏条件下对评估矩阵进行扩展。常用的矩阵扩展方法有基于数据复制和基于时间分段的矩阵扩展方法，基于数据复制的矩阵扩展方法可能导致矩阵间相关程度过高，影响分析结果，基于时间分段的矩阵扩展方法需要更长时间来构建相同规模的随机矩阵。

为了解决这一问题，本文提出了一种基于虚拟传感器的矩阵扩展方法，根据已有真实的测量数据，虚拟出更多的传感器，将虚拟传感器的输出也作为矩阵的元素，从而增加矩阵的维数，满足高维随机矩阵的构建条件。本文采用的虚拟传感器为卡尔曼滤波器[19-20]，首先根据真实传感器的测量数据，采用卡尔曼滤波器估计测量系统的测量值，以此估计值作为虚拟传感器的输出。假设系统用一线性随机方程表示：

(13)

其中，xk为k时刻的系统状态；xk-1为k-1时刻的系统状态；yk为系统测量值；ξk和ηk分别为预测过程和测量的噪声，一般可视为高斯白噪声。首先由系统前一时刻值预测当前时刻值：

xk|k-1=Axk-1|k-1

(14)

其中，xk-1|k-1为k-1时刻状态估计量；A为系统参数；xk|k-1为k时刻估计值。然后由系统前一时刻的最小均方误差矩阵估计当前时刻的最小均方误差矩阵：

Pk|k-1=APk-1|k-1AT+ξk

(15)

其中，Pk|k-1为xk|k-1对应的协方差；Pk-1|k-1为xk-1|k-1对应的协方差。然后由当前估计的最小均方误差矩阵更新修正后的结果：

xk|k=xk|k-1+Gk(yk-Hxk|k-1)

(16)

其中，H为系统参数；Gk为卡尔曼增益，可以表示为式(17)所示形式。

Gk=Pk|k-1HT(HPk|k-1HT+ηk)

(17)

最后更新最小均方误差矩阵：

Pk|k=(I-GkH)Pk|k-1

(18)

卡尔曼滤波器不需要精确建模，按照式(14)—(18)不断进行迭代运算即可得到最终的仿真结果。假设某传感器输出为：

y(t)=sin(100πt)+0.1n(t)

(19)

其中，n(t)为高斯白噪声。假设噪声幅值是信号幅值的10%，卡尔曼滤波器的输出如图2所示。

图2 卡尔曼滤波器仿真波形Fig.2 Simulative waveforms of Kalman filter

为了评估该卡尔曼滤波器输出的有效性，按式(20)计算滤波器的输出波形和原始波形相比的绝对百分误差(MAPE)，得到MAPE为3.36 %，可见该虚拟滤波器虽然存在一定的误差，但也能较为真实地反映原始信号，可用于矩阵扩展。

(20)

其中，S为滤波器输出的离散点数；fk为预测值。

2.3 评价指标

线性特征值统计量(LES)能够反映一个随机矩阵的特征值分布情况。对于一个随机矩阵W，λi为矩阵W的特征值，平均谱半径(MSR)是LES的一种类型，其定义为λi在复平面上分布的平均值，即：

(21)

其中，E()表示平均值函数；n2为特征值的总数。

对于标准矩阵积Dstd而言，其MSR可以表示为式(22)所示形式。

(22)

其中，λwi为Dstd的特征值。对于一个随机矩阵而言，单个特征值无法反映时间窗内矩阵元素的统计规律，而矩阵的迹能够反映矩阵元素的统计特征。MSR是一个随机变量，反映了随机矩阵的迹，可将其作为电子式互感器误差状态与影响量的相关性评估指标。

利用误差状态矩阵和高斯白噪声矩阵构造一个参考矩阵Dref，通过比较评估矩阵和参考矩阵的MSR，可以分析误差状态与影响量之间的相关性。定义评估矩阵和参照矩阵的MSR之差为dMSR，dMSR及其对时间的积分IMSR可以表示为：

(23)

其中，εev为基于评估矩阵得到的MSR；εref为基于参考矩阵得到的MSR；t1和t2分别为评估的起始时刻和结束时刻。评价指标dMSR、IMSR可以定量地表征电子式互感器误差状态和影响量的相关性。

基于随机矩阵理论的电子式互感器误差状态相关性分析方法的实施步骤如图3所示。

图3 相关性分析方法实施步骤Fig.3 Implementation steps of correlation analysis

具体步骤如下。

a. 数据提取：采集电子式互感器的误差数据以及误差影响量数据。

b. 评估矩阵构建：根据采集到的数据构建影响量相关性评估矩阵，同时进行矩阵扩展。

c. 评价指标计算：将生成的高维随机矩阵经过标准化处理后，得到标准矩阵积，进而求出矩阵的特征值分布和评价指标。

d. 相关性分析：通过比较分析评价指标，评估电气影响量和非电气影响量对电子式互感器误差状态的影响程度，若dMSR发生突变，则表明影响量对电子式互感器的误差状态造成了影响；否则表明电子式互感器误差状态与影响量的相关性小；IMSR越大，则表明影响量对电子式互感器的误差状态的影响程度越大。

3 算例分析

3.1 数据来源

算例中的数据源自如图4所示的220 kV互感器误差状态监测平台一天内的数据。

图4 互感器误差状态监测平台基本架构Fig.4 Basic structure of monitoring platform for error state of electronic transformer

a. 线路间隔安装有电磁式电流互感器和空心线圈电流互感器，2个互感器的准确度均为0.2级，额定电流均为600 A。电磁式互感器的额定输出为5 A，额定二次容量为25 V·A，额定电流下的比差为0.08%、角差为6′；空心线圈电流互感器在额定电流下的比差为0.12%、角差为6′，输出遵循IEC61850-9-2协议[21]。信号采集单元将电磁式电流互感器的模拟信号转换为数字信号。数据处理单元接收信号采集单元的输出信号及采样值报文数据，满足0.05级 的准确度要求，并以电磁式电流互感器输出为标准得到误差比对结果。

b. 环境监测单元负责采集环境参量，包括温度、湿度、振动、磁场。光纤远传单元负责将环境监测单元的数据进行标准化处理，送给另一台数据处理单元。数据处理单元将数据通过交换机网络传输给服务器，服务器对数据进行存储和分析。时钟同步单元建立时钟同步网络，同步方式采用IRIG-B码对时方式[22]。

图4中的空心线圈电流互感器比差、角差与时间的关系如图5所示。由图可见，其比差从0.03%变化到0.098%，角差从-9.94′ 变化到 -20.43′。

图5 空心线圈电流互感器的比差和角差Fig.5 Ratio error and phase error of air-core coil current transformer

误差状态监测平台中的误差影响量和时间的关系如图6所示(图6(b)中，湿度为相对湿度)。由图可见，温度影响量的变化范围为19.6～28.5℃，湿度的变化范围为65.5%～94.6%，振动的变化范围为0.04～ 0.09 g；磁场保持在0.05～0.08 Gs范围内；负荷的变化范围为1.9%～4.5%。

图6 误差状态影响量数据Fig.6 Influencing factors of error state

将非电气影响量、电气影响量、组合影响量(包括非电气影响量与电气影响量)与电子式互感器的误差状态数据分别构成原始矩阵，基于卡尔曼滤波器对原始矩阵进行扩展，数据规模如表1所示。

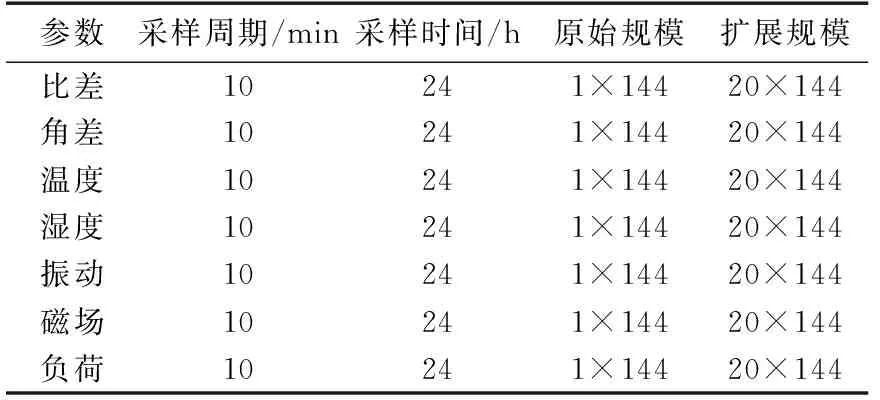
表1 相关性分析矩阵规模Table 1 Matrix scale of correlation analysis

3.2 误差状态与非电气影响量的相关性分析

首先分析空心线圈电流互感器误差状态和非电气影响量之间的相关性。将空心线圈电流互感器的比差数据构成误差状态矩阵，将温度数据构成误差影响量矩阵，误差状态矩阵和误差影响量矩阵合并为评估矩阵Dev1，矩阵规模为40×144；仿照评估矩阵Dev1的构造方法，将空心线圈电流互感器的比差数据和湿度数据合并成评估矩阵Dev2，矩阵规模为40×144。通过矩阵Dev1和Dev2评估空心线圈电流互感器的比差和温度、湿度之间的相关性。

图7 Dev1和Dev2的奇异值等价矩阵特征值分布Fig.7 Eigenvalue distribution of singular value equivalent matrix for Dev1 and Dev2

基于高维随机矩阵理论，可以计算评估矩阵Dev1和Dev2的奇异值等价矩阵的特征值，特征值分布如图7所示(图7中因制图尺寸调整呈椭圆形，实际特征值分布为圆环，后同)。由图7可见，Dev1的奇异值等价矩阵的特征值分布较为分散，且部分特征值超过了圆环的限制；与之相反，Dev2的奇异值等价矩阵的特征值分布较为集中，基本分布在圆环内。

滑动时间窗选取为30 min，计算相关性评价指标，计算结果如图8所示。由图可以看出，评估矩阵Dev1的评价指标dMSR的最大值上升到了0.35附近，IMSR达到了181.65，而评估矩阵Dev2的评价指标dMSR始终保持在0附近，且IMSR为43.8，要远小于Dev1的IMSR，这表明温度和空心线圈电流互感器的比差之间存在较强的相关性，而湿度和空心线圈电流互感器比差的相关性较弱。

图8 比差评估矩阵的评价指标Fig.8 Evaluation index for ratio error evaluation matrix

将利用空心线圈电流互感器的比差数据构成误差状态矩阵，温度、湿度数据、振动构成误差影响量矩阵，构建评估矩阵Dev3，矩阵的规模达到80×144。基于高维随机矩阵理论，得到如图9(a)所示的评估矩阵Dev3的奇异值等价矩阵的特征值分布，可以看出Dev3的奇异值等价矩阵的部分特征值分布超过了圆环的限制。依然取滑动时间窗为30 min，计算相关性评价指标，计算结果如图9(b)所示。可以看出评价指标dMSR发生了变化，而IMSR达到了376.05。

图9 Dev3的奇异值等价矩阵的特征值分布和评价指标Fig.9 Eigenvalue distribution and evaluation index of singular value equivalent matrix for Dev3

同理还分析了空心线圈电流互感器的比差和振动的关联关系，得到的IMSR计算结果为34.15，这表明空心线圈电流互感器比差和振动的相关性较弱。根据上述分析结果，可以推断空心线圈电流互感器的比差和温度相关性较强，和湿度、振动的相关性较弱。

另外，在多种影响量叠加作用的前提下，基于高维随机矩阵的相关性分析方法同样可以分析电子式互感器误差状态与影响量的相关性。需要注意的是，根据Dev3得到的结果反映的是这些影响量的总体影响，而无法细分单一影响量和误差状态的相关性。如需分析单个影响量对误差状态的影响，将误差状态数据和单个影响量数据构成评估矩阵即可。

利用角差数据构成误差状态矩阵，将温度数据、湿度数据、振动数据构成误差影响量矩阵，合并后形成评估矩阵Dev4，矩阵的规模为80×144。根据Dev4得到奇异值等价矩阵的特征值分布，如图10(a)所示，可以看出特征值基本分布在圆环内。由Dev4计算的相关性评价指标如图10(b)所示。可以看出评价指标dMSR均保持在0附近，IMSR为65.55，这表明空心线圈电流互感器角差和组合非电气影响量的相关性较弱。

图10 Dev4的特征值分布和评价指标Fig.10 Eigenvalue distribution and evaluation index of singular value equivalent matrix for Dev4

3.3 误差状态与电气影响量相关性分析

本节分析空心线圈电流互感器误差状态与电气影响量的相关性。利用空心线圈电流互感器的比差数据构成误差状态矩阵，利用磁场、负荷数据构成误差影响量矩阵，将误差状态矩阵和误差影响量矩阵合并为评估矩阵Dev5，矩阵的规模为60×144。将空心线圈电流互感器的角差数据构成误差状态矩阵，将磁场、负荷数据构成误差影响量矩阵，状态数据矩阵和误差影响量矩阵合并为评估矩阵Dev6，矩阵的规模同样为60×144。得到评估矩阵Dev5和评估矩阵Dev6的奇异值等价矩阵的特征值分布如图11所示，可以看出特征值的分布较为分散，向圆心靠近，且均超出了圆环的限制。

图11 Dev5和Dev6的奇异值等价矩阵特征值分布Fig.11 Eigenvalue distribution of singular value equivalent matrix for Dev5 and Dev6

评估矩阵Dev5的相关性评价指标的计算结果如图12(a)所示，可以看出，对于评估矩阵Dev5而言，评价指标dMSR发生了变化，IMSR达到了352.65，这表明电气影响量和空心线圈电流互感器比差之间的相关性较强。评估矩阵Dev6的相关性评价指标的计算结果如图12(b)所示，可以看出，评价指标dMSR发生了变化，且IMSR为424.65，这说明电气影响量和空心线圈电流互感器角差之间的相关性也较强。

图12 Dev5和Dev6的评价指标Fig.12 Evaluation index of Dev5 and Dev6

3.4 误差状态与组合影响量相关性分析

本节分析空心线圈电流互感器误差状态与组合影响量之间的相关性。将空心线圈电流互感器的比差数据构成误差状态矩阵，将包括温度、湿度、振动、磁场、负荷数据在内的组合影响量构成误差影响量矩阵，将2个矩阵合并为评估矩阵Dev7，矩阵规模为120×144。

利用角差数据构成误差状态矩阵，将包括温度、湿度、振动、磁场、负荷数据在内的组合影响量构成误差影响量矩阵，2个矩阵合并为评估矩阵Dev8，矩阵的规模同样为120×144。评估矩阵Dev7和评估矩阵Dev8奇异值等价矩阵的特征值分布如图13所示，可以看出评估矩阵Dev7和评估矩阵Dev8的特征值分布不再局限于圆环内。

图13 Dev7和Dev8的奇异值等价矩阵特征值分布Fig.13 Eigenvalue distribution of singular value equivalent matrix for Dev7 and Dev8

评估矩阵Dev7的相关性评价指标的计算结果如图14(a)所示，由图可见，评价指标dMSR发生了突变，IMSR为334.5，这表明组合影响量和空心线圈电流互感器比差之间的相关性较强。评估矩阵Dev8的相关性评价指标的计算结果如图14(b)所示，由图可见，评价指标dMSR发生了突变，IMSR为356.85，这表明组合影响量和空心线圈电流互感器角差之间的相关性也较强。

图14 Dev7和Dev8的评价指标Fig.14 Evaluation index for Dev7 and Dev8

4 结论

本文将随机矩阵理论应用于电子式互感器误差状态相关性分析，具体工作包括：提出了基于高维随机矩阵理论的相关性分析方法以及实施步骤，建立了dMSR以及IMSR这2个相关性评估指标；研究了基于卡尔曼滤波器的矩阵扩展方法，实现了稀疏条件下高维随机矩阵的扩展。采用本方法对220 kV变电站互感器误差状态监测平台的运行数据进行了分析，可以得到以下结论：

a. 将高维随机矩阵理论应用于电子式互感器误差状态与影响量的相关性分析是可行的，该方法可以实时确定互感器误差与1个或者多个环境参量的关联程度，基于1个或者多个环境参量的分析均能得到一致的结果；

b. 在运空心线圈电流互感器比差和温度、磁场以及负荷影响量的相关性较强，和振动、湿度影响量的相关性较弱；角差和电气影响量的相关性较强，和非电气影响量的相关性较弱；

c. 实际工程中需要尽量抑制温度和磁场影响量对空心线圈电流互感器的作用，以保证在运空心线圈电流互感器误差状态的稳定性。