考虑负荷纵向随机性的用户用电行为聚类方法

冯志颖，唐文虎，吴青华，陆国俊，栾 乐

1. 华南理工大学 电力学院，广东 广州 510640；2. 广州供电局有限公司，广东 广州 510000)

0 引言

智能电网是能源与电力行业发展的必然趋势[1]。随着智能电网理论与实践的推进，电网建设正朝着数字化、互动化和分布化的方向发展[2]。分布式可再生能源和电动汽车等多元化负荷的广泛接入，加大了负荷预测和需求侧管理等工作的难度，对电力用户进行精细化分类成为了负荷预测、需求侧管理、用电定价等方面的重要前提。对用户进行合理精细的分类，掌握用户的用电行为，对于各电力企业制定运维和营销策略具有重要意义。用户用电负荷具有较大的不确定性，日负荷曲线展现了用户1 d中的用电行为，表现为负荷的横向特性；而一段时期(如一周或一个月)中不同的日负荷曲线也会存在差异，表现为负荷的纵向特性。不同用户的纵向差异程度具有明显的区别。

国内外已有不少学者对负荷聚类进行了研究。主要的研究方法大致可分为改进相似度度量方法[3-6]、改进数据预处理方法[7-9]和改进聚类算法[10-13]。在改进相似度度量方法方面，文献[3]针对传统欧氏距离度量负荷曲线形态的不足，提出以余弦相似度代替欧氏距离，能较好地度量负荷形态之间的差异;文献[4]利用双向夹逼的思想，结合层次聚类对同一用户的不同负荷日进行聚类，该方法主要用于寻找相似日进而进行负荷预测，但不适用于聚类不同的电力用户;文献[5]提出以余弦相似度作为外层聚类根据、以欧氏距离作为内层聚类根据的双层聚类方法，其能够识别不同的负荷形态和大、小负荷。在改进数据预处理方面，文献[6]利用6个日负荷特性指标取代高维的时间序列进行聚类，提高了算法的运算速度和鲁棒性，但在一定程度上会造成负荷数据失真;文献[7]利用快速小波变换提取负荷时间序列的特性指标;文献[8]通过多尺度分析解决电力负荷数据的数据量大、波动性和不确定性的问题;文献[9]比较了多种降维方法的效果，指出主成分分析和Sammon映射的聚类效果最好。在改进聚类算法方面，用于负荷聚类的聚类算法主要有KernelK-means[10]、自组织映射神经网络[11]、密度空间聚类[12]、C-vine Copula混合模型[13]等算法。文献[10]引入核函数改进传统的K-means算法，将数据映射到高维空间，从而提高数据的可分性;文献[11]利用自组织映射神经网络，对原始数据进行低维映射，实现了聚类效果的可视化;文献[12]结合引力搜索算法和密度空间聚类对居民用电数据进行聚类，并分析各类用户的需求侧响应潜力;文献[13]提出一种基于模型的C-vine Copula混合模型聚类算法，具有较好的聚类效果，但其计算过程复杂，计算时间较长。

已有的研究大多针对负荷的横向特性，对于多日的日负荷曲线的预处理，只是简单地取平均值，或者剔除异常值后选取其中的某天作为典型负荷日等，缺乏对负荷纵向特性的考虑，而且预处理过程会造成部分有用信息的丢失。在以下的场景中，对用户进行聚类时应该考虑负荷纵向波动性：用户每天的负荷曲线变化很大，难以用一条典型负荷曲线表征其用电行为；异常用电行为分析；区间或概率性负荷预测等。针对这种不确定性，文献[8]提出一种利用高斯混合模型来反映用户的纵向随机性的方法，取得了一定的效果，但算法计算过程复杂。

本文提出一种同时考虑负荷横向与纵向特性的负荷聚类算法，并首次引入推土机距离(EMD)算法，以衡量在同一时刻不同用户之间的负荷纵向距离；然后对所有时刻进行综合，得到用户之间的综合距离；最后利用美国能源部提供的公开负荷数据，与传统的只考虑负荷横向特性的层次聚类算法以及其他相似度度量方法进行比较，证明本文方法的合理性与准确性。

1 负荷行为识别方法

1.1 负荷的纵向随机性

电力用户的用电行为除了可用日负荷曲线描述之外，还应包括负荷的纵向随机性。负荷的纵向随机性表现为用户在一段时间的负荷波动性。某些用户的用电负荷每天的差异较小，表现为较大的稳定性；某些用户的用电负荷受外界影响较大，表现为较大的波动性。此外，同一用户在不同时刻表现出来的波动性也有所不同。

当用户多日的日负荷曲线形成一个非凸集时，取平均值后的曲线将不包含于此集中，即该平均后的曲线并不能代表用户的用电行为，这种取平均值的处理不仅会导致数据的丢失，还会导致错误的分类[9]。不同的负荷聚类方法关注的角度不同，适用于不同的领域。当用户每天的负荷曲线差异较大，或者应用于异常用电行为分析、区间或概率性负荷预测等场景时，对用户进行聚类时应该考虑负荷的纵向波动性。

1.2 相似度度量方法

相似度度量(距离度量)是衡量不同对象之间相互关系的方法[15]。定义相似度度量函数应该满足以下4个条件：非负性、自身距离为0、对称性以及三角不等性，分别如式(1)—(4)所示。

d(x,y)≥0

(1)

d(x,x)=0

(2)

d(x,y)=d(y,x)

(3)

d(x,y)+d(y,z)≥d(x,z)

(4)

其中，d(x,y)为对象x和y之间的距离。

除了下文重点介绍的EMD之外，衡量2个概率分布之间差异的距离函数还有 Bhattacharyya 距离(巴氏距离)[15]、KL距离(相对熵)[16]和卡方系数[17]，分别用DB、DKL和Dchi-sqr表示，其离散形式的具体计算公式分别如式(5)—(7)所示。

(5)

(6)

(7)

其中，P和Q为2个概率测度。

本文将在2.4节中分别利用包括EMD在内的 4种相似度度量方法对用户负荷进行聚类，比较各自的聚类效果。

1.3 EMD简介

Peleg等在文献[18]中最早提出EMD，Rubner等在文献[19]中提出将EMD 应用于图像识别中，自此EMD 被应用于衡量2个概率分布之间的差异。文献[20]证明了EMD满足相似度度量函数的4个条件。 Earth Mover’s Distance被译为推土机距离或者地球移动距离,顾名思义，其思想来源于一个生活问题：假设有若干数量的土堆，每个土堆的大小不相同且分布的位置不相同;同时存在若干数量的土坑，每个土坑的大小不相同且位置不相同;对于每个土堆-土坑对的运输成本是给定的(以距离表示),任务是把土堆搬动并填到土坑里，通过规划运输方案，使运输成本最低。

在直方图中体现EMD的示意图如附录中图A2所示，2个直方图分别表示土堆和土坑。假定2个直方图中分别存在m和n个直方，则2个直方图可以被分别描述为P={(p1,wp1),(p2,wp2),…,(pm,wpm)}和Q={(q1,wq1),(q2,wq2),…,(qn,wqn)}，其中pi和qj分别表示土堆和土坑直方的位置，wpi和wq j表示相对应直方的高度(土堆和土坑的大小)。2个直方图之间的EMD可以转化为如式(8)所示的线性规划问题[17]。

(8)

其中，fij为第i个直方到第j个直方的运输数量。

(9)

1.4 算法流程

对电力用户的横向和纵向特性进行聚类的思路如下：采集用户负荷数据集，该数据集包含了一段时间(如一个月)的日负荷曲线数据；归一化原数据；统计每个用户每一时刻的负荷值分布特性，形成该用户关于该时刻的分布直方图；利用EMD衡量2个用户在同一时刻之间的负荷差异；对所有时刻的距离值取均方根，得到2个用户的距离值，依此类推得到其他所有2个用户之间的距离值；利用所得到的距离信息，对所有用户进行层次聚类；根据聚类有效性指标确定聚类数，得到最终聚类结果。

1.4.1 数据归一化

(10)

(11)

(12)

1.4.2 异常尖峰数据的识别和修正

由式(12)可知，负荷序列的最大负荷值出现异常，即出现异常尖峰，会对归一化后的数据造成影响，恶化分布特性。因此在进行数据归一化之前，须先进行异常尖峰数据的识别和修正，如式(13)—(15)所示。若Δlk>μ+3σ，则认为该天最大负荷值异常，对该天最大负荷值作如式(16)、(17)所示的修正，否则不作处理。

(13)

(14)

(15)

Δlk′=μ+3σ

(16)

(17)

问：那么您刚刚提到“理论商店”，我想很多研究者在研究的过程中都会不可避免地和理论产生交集，尤其是年轻研究者可能会苦于还没有找到一个合适的解释理论，或者在了解理论的基础上苦于找寻不到自己明确的研究问题，那么您是如何定义研究中生成的理论呢？以及一个理论在研究中的作用呢？

1.4.3 负荷数据的纵向统计

对负荷数据进行归一化后，每个用户每天的负荷值将归一化到区间[0,1]中，再将区间[0,1]精细划分为20个区间，每个小区间长度为0.05。对负荷数据的纵向分布特性进行统计，将若干天同一时刻的负荷值分进上述20个区间中，得到某一用户关于该时刻的分布直方图。用户i在时刻k的负荷分布情况如式(18)所示。

(18)

其中，pj为第j个直方(负荷区间)的中心位置；wj为第j个直方的高度，即位于该负荷区间的天数。

图1为2个用户在时刻08∶00 30 d的负荷分布情况，可见与用户2相比，用户1在该时刻的用电行为随机性更大。从定量角度出发，2个用户在该时刻的负荷分布情况可以表示为：P18={(0.025,0),(0.075,0),…,(0.425,1),(0.475,8),…,(0.575,5),(0.625,12),(0.675,1),…,(0.925,0),(0.975,0)}；P28={(0.025,0),(0.075,0),…,(0.575,1),(0.625,11),(0.675,16),(0.725,1),(0.775,1),…,(0.925,0),(0.975,0)}。

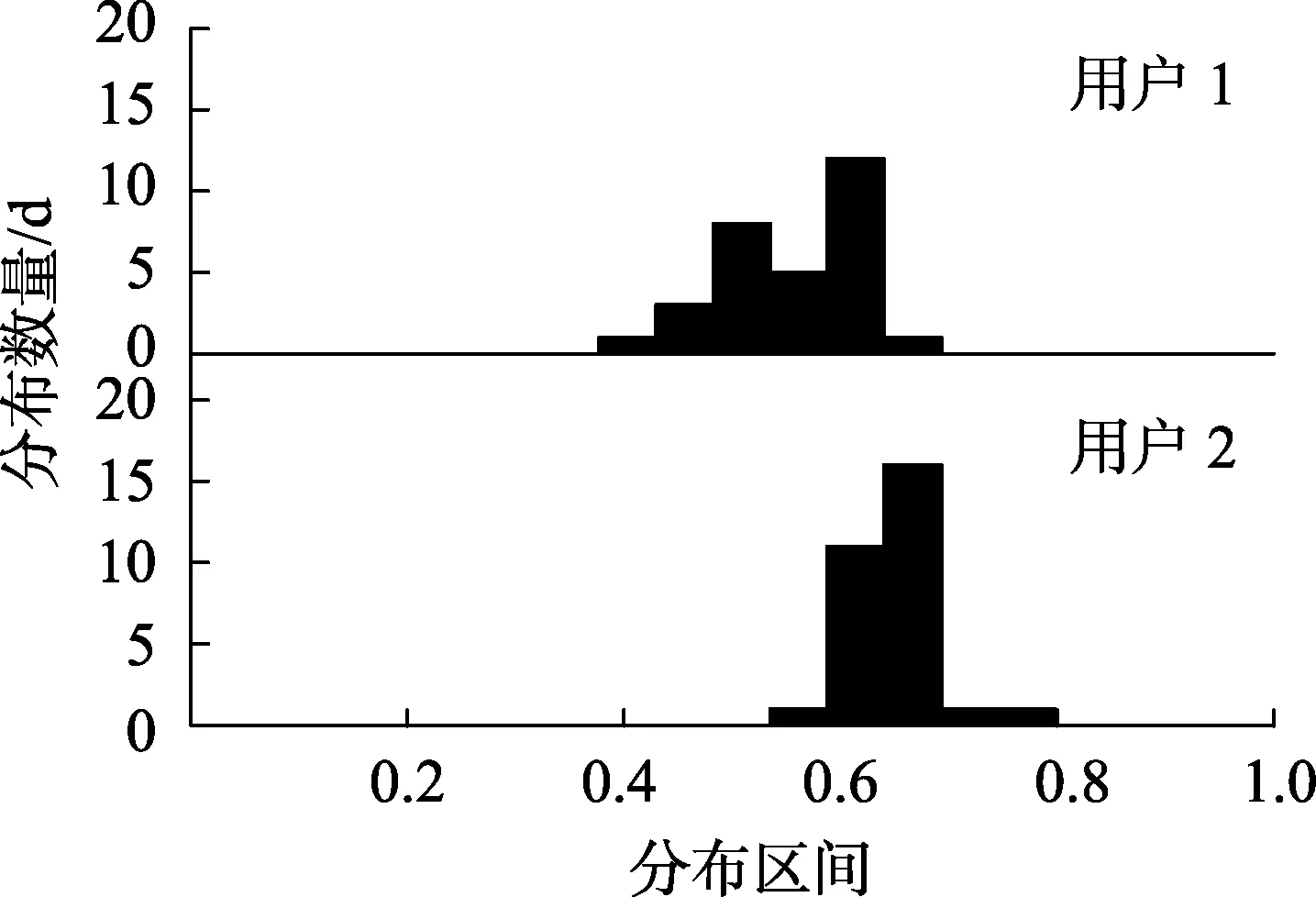
图1 2个用户在同一时刻的负荷分布直方图Fig.1 Distribution histograms of two users’ power consumption at the same time

1.4.4 用户用电行为差异性的衡量

利用1.3节介绍的EMD对2个用户在同一时刻的负荷分布直方图进行计算。由式(8)可以看出，利用EMD计算2个直方图之间的差异时，并不要求二者的直方面积一致，因此对数据的完整性要求较低，即使1 d中某一时刻的数据缺失，甚至一整天的数据缺失，也不影响计算结果。对2个用户所有时刻的距离值求取均方根，该结果即为2个用户用电行为差异的度量值。具体的计算公式如式(19)、(20)所示。

(19)

(20)

1.4.5 聚类效果评价指标

由于目前对双向负荷聚类的研究很少，尚缺乏综合衡量此聚类效果的指标，故本文定义如下2个聚类评价指标：负荷横向波动系数TLFC(Transverse Load Fluctuation Coefficient)和负荷纵向波动系数LLFC(Longitudinal Load Fluctuation Coefficient)，分别用于衡量用户横向与纵向特性的一致性，以二者的乘积作为聚类效果的综合指标。分别用fTLFC和fLLFC表示某类用户的TLFC值和LLFC值，其计算公式分别如式(21)、(22)所示。

(21)

(22)

2 算例分析

本文选取一组由美国能源部公开能源信息网站提供的居民用电负荷数据为研究对象，数据集包含936个居民用户1 a的用电负荷数据，每60 min采集一次，1 d共计24个测量点。

2.1 确定聚类数目

本文所选用的基于层次的聚类方法本质上是无需预先确定聚类数，可以在得到树状图之后根据不同的需要确定聚类数目，并据此对树状图进行分割，但这种处理方法对于聚类数的确定过于主观。为了使聚类数的确定更具客观性，本文利用3个有效性指标确定聚类数，并选取其中2个聚类指标：HS(Homogeneity-Separation)指标和CH(Calinski-Harabasz)指标综合确定最佳聚类数。2个指标值的具体计算公式分别如式(23)、(24)所示。

(23)

(24)

其中，a为聚类的数目；tr()表示矩阵的迹；SB(a)为聚类数a下的类间离差矩阵；SW(a)为聚类数a下的类内离差矩阵；R(s,t)为样本s和样本t之间的距离；ni和nj分别为第i个聚类Ci和第j个聚类Cj的样本数。

HS和CH指标均以曲线中的最大值点对应的聚类数作为最佳聚类数。由附录中图A3可知，利用HS和CH指标得到的最佳聚类数均为4，故选取4作为本算例的聚类数。

2.2 用户聚类结果

选取聚类数为4进行层次聚类后，将每一类中所有用户的负荷箱形图进行综合，垂直方向上矩形盒越长，表明该类用户在这一时刻的纵向波动性较大。用户的负荷横向特性可由矩形箱的中位数点所连曲线表示。通过聚类得到的每一类用户的综合箱形图如图2所示，图中负荷为标幺值。

图2 基于EMD聚类算法的用电行为箱形图Fig.2 Box diagram of power consumption behavior based on EMD clustering algorithm

2.3 聚类结果比较

为了进一步地从定量的角度证明本文所提方法的合理性，采用传统方法，即利用相同的数据集，取相同的聚类数，将一个用户多日的负荷数据取平均值作为该用户典型日负荷曲线，然后利用层次聚类算法聚类典型日负荷曲线。得到2种方法下的各类包含的用户数如附录中表A1所示。经过对比分析可知，类别3和类别4的用户标号一致，即聚类结果相同，类别1和类别2的聚类效果存在差异。

为了比较2种方法的聚类效果，附录中表A2比较了本文方法和传统方法以及未进行聚类时各个类别的综合聚类指标(fTLFCfLLFC)，表中数值越小，则表示同一类别中各个用户在一个月内的用电行为越相近。由此可知，相较于未进行聚类的指标值，2种方法中各个类别的综合聚类指标值都有较大程度的降低。然后比较本文方法和传统方法，在类别1和类别2中，本文方法的综合聚类指标比传统方法分别低4.1%和1.4%。结果表明本文方法相较于传统方法具有更高的合理性。

2.4 不同度量方法的比较

卡方系数也能粗略地对用户进行区分，但计算卡方系数所形成的4个类别的综合聚类指标分别为0、0.004 1、3.551×10-4和1.355×10-5，与附录中表A2结果相比，聚类效果明显不如EMD。进一步地观察利用卡方系数所形成的距离矩阵可知，矩阵内存在大量完全相同的距离值，造成该现象的原因在于：当2个概率分布重合部分较小，甚至完全分离时，无论分离得多远，计算得到的卡方系数都将保持不变。因此当样本之间差异较大时，卡方系数并不十分可靠。由此可见，采用EMD度量2个概率分布的差异具有较广的使用场合和更高的准确性。

3 结论

本文同时考虑了电力用户的负荷横向特性和负荷纵向特性，首次提出了基于EMD算法的负荷聚类方法。EMD算法相较于其他度量方法能够更好地度量2个分布之间的差异。比较了考虑和不考虑负荷纵向特性的聚类效果，结果表明本文方法能够同时对负荷的横向和纵向差异进行度量。在用户的负荷横向特性较为相似的情况下，通过对负荷纵向特性的有效反映，使得本文方法下的综合聚类指标比传统方法更低。由于EMD算法涉及较多的线性规划运算，运行效率不高，下一步的研究方向在于如何提高算法的运行速度，以及如何结合气象等因素进一步提高聚类的合理性。

附录见本刊网络版(http:∥www.epae.cn)。