基于混沌模拟退火粒子群优化算法的电动汽车充电站选址与定容

艾 欣，李一铮，王坤宇，胡俊杰

华北电力大学 新能源电力系统国家重点实验室，北京 102206)

0 引言

近年来，我国电动汽车的保有量迅速攀升，截至2016年底，我国电动汽车保有量已经接近100万辆，经测算，到2020年全国电动汽车保有量将超过500万辆[1]。电动汽车充电基础设施作为电动汽车发展的重要保障，其发展水平直接影响了电动汽车行业的发展速度和质量。目前，全国各地按照“桩站先行，适度超前”的原则，逐步推进充电基础设施的科学发展。根据需求预测结果，到2020年新增集中式电动汽车充换电站将超过1.2万座[1]。

电动汽车充电站的选址与定容问题是高维非线性数学问题，决策的优劣直接影响了其服务质量、效率、成本等。现有的国内外学者对城市电动汽车充电站的选址与定容问题研究仍处在起步阶段，没有形成系统完整的理论。文献[2]以投运至目标年综合费用最小为规划目标，利用变权Voronoi图的方法划分充电站的服务范围，并采用混合粒子群优化(PSO)算法求解，提高了算法迭代中后期的全局搜索能力。文献[3]将量子理论与粒子群优化算法结合，增强了优化算法的种群多样性以及算法的全局搜索能力。文献[4]结合了城市道路信息和电动汽车续驶里程，提出了电动汽车充电便捷系数，并利用Voronoi图理论和排队论确定充电站的容量。文献[5]将配电网约束等引入充电站规划模型中，同时以截获最大交通流量为目标进行规划，并采用快速非支配排序遗传算法-Ⅱ进行多目标优化规划求解。文献[6]引入了路网结构、车流信息、配电网络结构等约束进行优化规划。文献[7]综合考虑了城市路网和配电网的交互性，引入博弈论思想，并对电动汽车充放电特性对配电网供电可靠性的支撑作用进行了评估。文献[8]利用网格法确定充电站的站址，分析了充电站的盈利模型，提出了充电站的日负荷率、投资回收期、充电行驶里程、综合满意度4类评价指标。文献[9]将碳排放指标引入充电站选址定容规划模型中，采用Pareto最优前沿分析可选的方案，提出了基于需求点栅格化的充电站服务范围求解方法。文献[10]对电动汽车出行活动及充电过程进行预测，提出了基于电动汽车用户出行的规划模型，兼顾了电动汽车用户的出行需求以及充电站运营商的利益。

上述的研究均从一定的角度出发，提出了电动汽车充电站选址定容的模型，并采用了不同算法进行求解。本文在上述研究的基础上，提出了一种综合考虑全社会利益的选址定容规划模型。为了求解该模型，克服传统粒子群优化算法的早熟、局部收敛等缺点，本文将混沌理论与模拟退火算法与粒子群优化算法相结合，通过混沌理论优化粒子的搜寻空间，并用模拟退火算法的概率突跳特性改善粒子群优化算法的早熟问题；采用Voronoi图思想及需求点栅格化理论来确定充电站的服务范围；求解距离时引入了Floyd算法代替传统欧氏距离，使结果更加接近实际情况，进一步提高了算法的准确程度。

1 充电站选址定容的数学模型

目前主流的电动汽车能源补给方式主要为充电方式及换电方式2种，限于文章篇幅，本文暂未考虑换电方式，只针对充电方式进行探究。电动汽车充电站是社会的公共服务设施，在进行选址定容时不仅应考虑运营方的效益，还应考虑其社会服务作用。本文在考虑充电站运营方、电网企业的电力负荷均匀性、电力线路走廊、电动汽车车主的方便程度的综合基础上，提出了一种全社会成本最小化的电动汽车充电站选址定容优化规划数学模型，如式(1)—(7)所示。

minC=C1+C2+C3+C4

(1)

(2)

ArCA+Br+Lr]

(3)

C3=ε[Tr(CT+CP)+MrCM+ArCA+Br+Lr]

(4)

C4=365CeTe[Tr(CCu+CFe)+Mr(CL+CW)]

(5)

(6)

Nqγmaxyqr≤MrTe

(7)

其中，C1为电动汽车用户去往充电站路程产生的成本；C2为折算至每年的电动汽车充电站固定建设成本；C3为电动汽车充电站的年均运行维护成本；C4为电动汽车充电站的网损年费用；p为电动汽车行驶单位千米耗电量；Ce为电动汽车充电电价；dqr为从充电需求点q到电动汽车充电站r的距离；yqr为从充电需求点q是否去电动汽车充电站r充电的决策变量,且yqr∈{0，1}；Nq为充电需求点q需要充电的车辆数；r0为资金回收率；nk为充电站设计运行年限；Tr和CT分别为充电站r装设的配电变压器数目和配电变压器单价；Mr和CM分别为充电站r装设的充电机数目和充电机单价；CP为配电变压器改扩容折算至单台配电变压器的费用系数；Ar和CA分别为充电站r的用地面积和土地征用单价；Br为充电站r的基础设施建设费用；Lr为充电站r的电力走廊建设费用，表示由架空线更换为地下电缆所产生的费用；ε为将设备维护费用、折旧费用、员工工资折算到初期投资成本的折算系数；Te为充电站每天平均有效工作时间；CCu和CFe分别为折算至单台配电变压器的铜损和铁损；CL和CW分别为折算至单台充电机的线路损耗和充电损耗；Q为充电需求点的集合，且q∈Q={1,2,…,qmax}，qmax为充电需求点总数；R为电动汽车充电站集合，且r∈R={1,2,…,rmax}，rmax为充电站总数；γmax为需求点电动汽车最大同时充电率。式(6)、(7)为约束条件，式(6)表示每一个需求点到且只到一个充电站进行充电，式(7)表示充电站r服务范围内的需求充电车辆不应大于该站的服务能力。

2 混沌模拟退火粒子群优化算法

2.1 粒子群优化算法及其不足之处

粒子群优化算法是一种基于群体协作的随机搜索算法，其算法的中心思想源自对鸟群捕食行为的研究，自从其在1995年由Eberhart和Kennedy提出以来[11]，一直是广大学者的研究热点。其迭代形式如下：

(8)

(9)

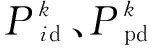
分析其迭代方程可以看出，粒子群优化算法在计算中虽然收敛速度较快，但非常容易陷入局部最优的情况。例如，处于全局最优位置的粒子其移动速度只由其自身的速度惯性决定，当自身速度为0时其将停止运动，当所有粒子被吸引运动到这个位置时将会停止搜寻。而在实际中，这个位置往往是局部极值。因此，为了将算法应用于充电站选址定容问题中，必须提高算法的全局搜索能力，避免过早陷入局部最优的情况。

2.2 算法的改进

为了解决粒子群优化算法后期收敛于局部极值的问题，本文提出了一种基于混沌理论和模拟退火算法的粒子群优化(CSAPSO)算法，引入模拟退火算法的概率突跳能力，使CSAPSO算法不但可以接受好的解，也能以一定的概率接受差的解，在退火温度的控制下能有效地提高全局搜索能力。同时引入混沌理论对r1、r2进行动态赋值，使粒子种群的运动行为更加优化。CSAPSO算法的计算步骤如下。

a. 初始化参数：惯性权重ω、学习因子c1和c2、退火速度δ。

b. 随机生成包含m个粒子的种群，随机初始化粒子的位置和速度，在电动汽车充电站问题中粒子的位置与速度均为正整数。

c. 计算每个粒子i的适应度，记录各个粒子位置Pid和全局最优位置Ppd。

d. 选出整个种群的最优适应度Zbest，计算得到退火算法初始温度T。

e. 计算得到当前温度下各个Pid的退火算法适应度如下：

(10)

其中，f(Pid)为粒子位置在Pid时的粒子群优化算法适应度值；f(Ppd)为粒子群最优适应度值。

f. 采用轮盘赌输的策略，从所有个体最优位置Pid中选出一个值代替全局最优位置，将其存入Pzd中。

g. 用Pzd代替Ppd，代入式(8)中更新各个粒子的速度如下：

(11)

h. 计算各个粒子的适应度值，更新各粒子的最优位置Pid和种群最优位置的Ppd。

i. 按照下式进行退火操作：

T=δT

(12)

j. 判断是否满足算法终止条件(电动汽车充电站选址问题中为预设的迭代次数)，若满足则停止搜索，输出计算结果，否则转至步骤e。

2.3 相关参数的设置

a. 惯性权重的设置。

惯性权重表示粒子过去飞行状态对当前状态的影响，其值直接决定了粒子种群的全局寻优能力和局部寻优能力。本文采取文献[12]提出的线性递减策略调整惯性权重。在算法运行初期，较大的惯性权重确保了粒子群可以进行大范围的全局搜索，以较快的速度确定最优解的大致位置。在迭代中后期，惯性权重的缩小使粒子群能在局部更加精确地搜寻最优解。设置公式如下：

(13)

其中，ωstart和ωend分别为起始和终止的惯性权重值，一般分别设置为0.9和0.4；kmax和k分别为迭代次数和当前迭代数。

b.r1、r2的设置。

本文采用混沌理论对r1、r2进行动态调整。采用Logistic模型产生混沌序列[13]如下：

(14)

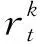
c. 初始温度设置。

算法中初始温度T直接影响了模拟退火算法的全局搜索能力，较高的初始温度可以显著提高搜索到全局最优解的可能性。设置公式如下：

(15)

其中，Zbest为初始粒子种群中最优的适应度值。

d. 退火速度设置。

模拟退火算法运行中，模拟的退火过程越慢，算法找到全局最优的概率就越大，本文将退火速度设置为0.95。

3 基于CSAPSO算法的充电站选址定容

3.1 规划假设

基于上文提出的电动汽车充电站选址定容规划模型，做以下假设。

a. 选择城市的交通节点为电动汽车充电站的候选站址，现实中应根据实际情况选取。

b. 将所有需求充电的车辆整合到距离其最近的交通节点，将每个交通节点看作一个充电需求点，在实际规划过程中充电需求量可结合交通节点典型日车流量数据和目标年电动汽车占比获得。

c. 假设每一个需求点的车辆到且仅到距离其最近的充电站进行充电。根据Voronoi图原理和需求点栅格化理论[14]，即规定充电站的服务范围为到该充电站实际距离(由Floyd算法求得)最近的需求点的集合。

3.2 服务范围划定及Floyd算法概述

根据栅格化理论的思想，将城市道路和交通节点组成的二维图形视作栅格化后的图形。按照假设将道路上需要充电的车辆和每个栅格内的需要充电的车辆整合到道路节点处，将交通节点看作充电需求点。

划分充电站的服务范围：将充电站的选址集合看作二维平面上的点集，充电需求点视为平面上的点。根据Voronoi图原理可知，充电站服务范围内的充电需求点到该站的实际距离应小于等于充电需求点到其他充电站的实际距离。

本文采用Floyd算法求实际距离，Floyd算法的具体步骤如下。

a. 根据规划新区实际道路情况生成城市道路CAD图，并对各道路节点进行编号。

(16)

其中，l,j=1,2,…,b；wlj为道路节点l到j之间的实际道路长度。

c. 对于任何2个道路节点l和j，判断是否存在一个中间节点s，使节点l通过节点s再到节点j的距离小于现有的距离，如果存在这样的节点s，则更新迭代距离矩阵D(k)，如式(17)所示。

(17)

d. 按照上述规则更新迭代获得距离矩阵D(k+1)，若D(k+1)≠D(k),则返回步骤c；否则终止迭代，得到最短路径矩阵即为D(k)。

3.3 规划流程

具体规划流程如下。

a. 初始数据处理。处理规划目标城市道路交通信息及车流量信息，生成城市道路CAD图，得到各需求点充电需求量。以充电站最大服务容量、最小服务容量以及总充电需求量来估算最大建站数nmax和最小建站数nmin。

b. 充电站规划的粒子群编码。电动汽车充电站选址定容包含两部分内容：站址的确定和站规模的确定。因此粒子编码形式如下：

X=[x1,x2,…,xn,y1,y2,…,yn]n∈(nmin,nmax)

(18)

其中，xg为互不重复的正整数，表示第g个充电站选在备选位置xg处；yg为正整数，表示第g个充电站的规模等级。例如n=4时，X=[15,9,31,19,1,4,4,3]表示在备选站址15、9、31、19处建站，站规模等级分别为1、4、4、3。

c. 按照编码形式生成初始粒子种群和粒子速度，在充电站选址定容问题中，粒子位置与速度的分量均为正整数，因此在算法中应进行取整操作。

d. 根据规划模型求出个体适应度值和全局最优值(模型中涉及的距离均采用Floyd算法求解)，按照式(15)求出模拟退火算法初始温度。

e. 采用CSAPSO算法更新粒子群的位置与速度，并记录全局最优适应度值。

f. 循环操作步骤c—e。求出不同建站数n的最优适应度值及选址定容方案。

采用CSAPSO算法进行电动汽车充电站选址定容的规划流程如附录中图A1所示。

4 算例分析

以某典型新区的电动汽车充电站选址定容为例进行分析，该新区规划总面积为26.75 km2，东西跨度为6.4 km，南北跨度为5.3 km,含有道路78条。该新区的道路节点图如图1所示，图中的道路节点处数字为该节点的编号。各道路节点及其典型日的车流量见附录中表A1。

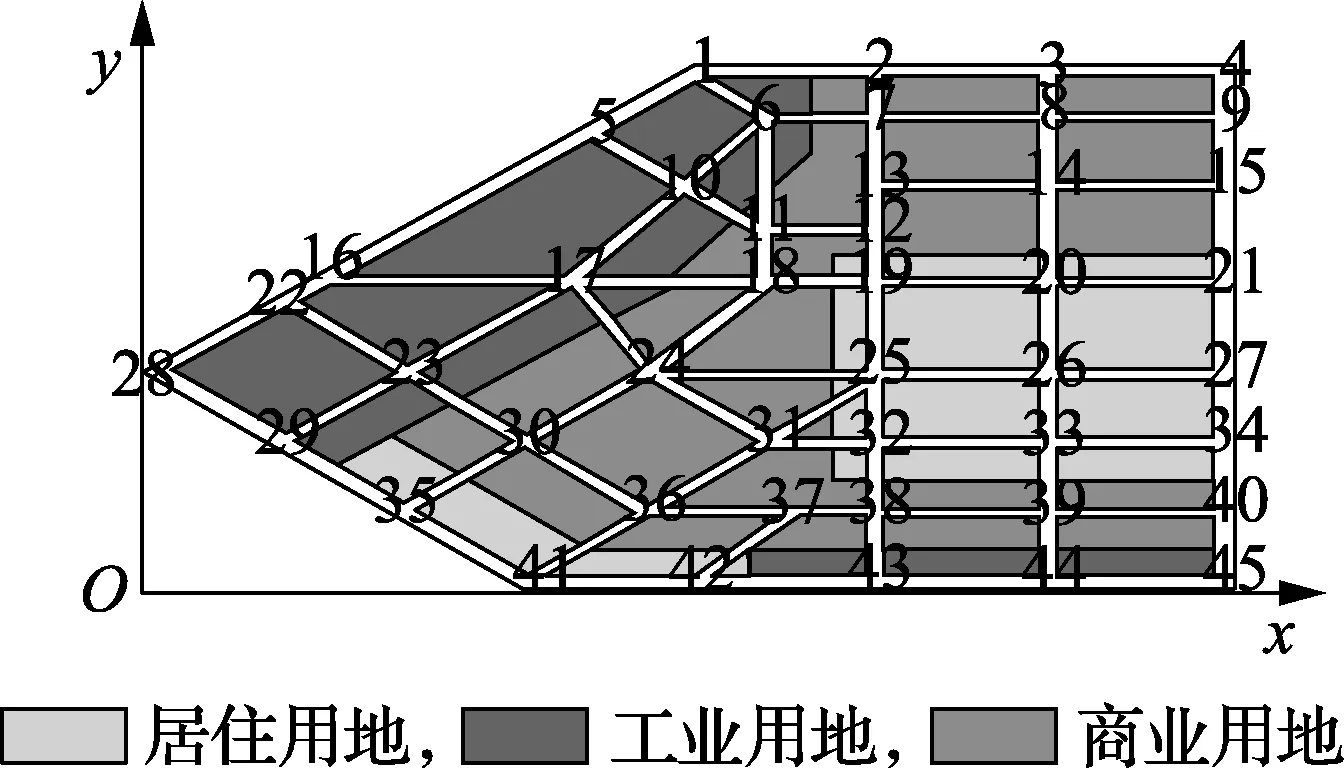
图1 规划新区道路节点Fig.1 Road nodes of new planning district

规划在该新区建设适当的电动汽车充电站，使充电站的全社会成本最小。假设充电站的使用运行年限为20 a，每辆电动汽车电池平均容量为50 kW·h。根据文献[15]对电动汽车充电站等级及各项指标的划分，合理假设电动汽车充电站的基本参数如附录中表A2所示，表中建设成本为充电机成本、配电变压器成本以及基础建设成本之和，不包含用地成本。该新区各类型土地出让价格如附录中表A3所示。

由于现有的车辆群体是汽油车与电动汽车的混合群体，所以假设至规划目标年电动汽车所占的比例为10%，结合附录中表A1的数据可知，分别按照单位日最小服务能力和最大服务能力配置充电站时，可以计算得到分别需要3座和18座充电站。随着充电站数目的增多，虽然降低了用户的充电路程成本，但同时增加了充电站建设成本。所以经过合理的筛选规划，可以得出该新区建设充电站数目为3～7座。采用CSAPSO算法进行计算的各项参数值见附录中表A4。

CASPSO算法参数如下：粒子种群规模为50，起始惯性权重值ωstart=0.9，终止惯性权重值ωend=0.4，退火速度δ=0.95，学习因子c1=c2=1.494 45，终止迭代次数为200次。通过计算可得当建设3～7座充电站时，全社会成本如图2所示。可见当建设4座充电站时，可满足该算例中用户充电需求并且使全社会成本最优。当建设4座充电站时，各充电站选址、等级及其服务范围如表1所示。各项成本如下：C1=204.5万元，C2=363.9万元，C3=407.8万元，C4=365万元。

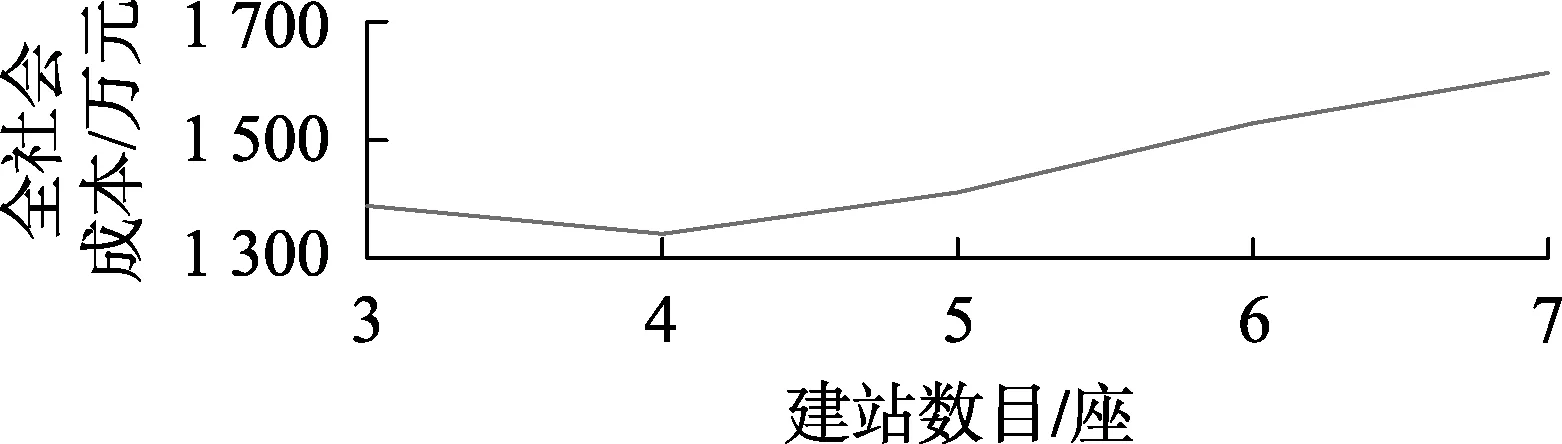
图2 建站数目及对应成本Fig.2 Cost of station vs. number

充电站建站道路节点建站等级服务道路节点12042—4,6—9,11—15,18,19,21226424,25,27,31—34,36—45322123,28—30,3541621,5,10,17

为了验证算法的优化能力，当建站数目为4座时，分别采用粒子群优化算法和CSAPSO算法对该算例进行求解，得出2种算法的最佳适应度曲线如图3所示。由实验数据可知，粒子群优化算法在迭代第25次时求得其最佳适应度值为1 360.7万元；CSAPSO算法在迭代第130次时求得最佳适应度值为1 341.2万元。对比图3中2条曲线可知，迭代初期粒子群优化算法收敛的性能优于CSAPSO算法，并于较少的迭代次数时收敛，而CSAPSO算法在迭代的中后期仍保有较好的种群多样性，其最终综合优化结果优于粒子群优化算法。最终求得的建站位置及其服务范围示意图如图4所示。

图3 2种算法最佳适应度曲线对比Fig.3 Comparison of best fitness curve between two algorithms

图4 建站位置及其服务范围示意图Fig.4 Schematic diagram of charging station location and its service range

5 结论

本文考虑了充电站运营方、电网企业的电力负荷均匀性、电力线路走廊、电动汽车车主的方便程度等多方面因素，对选址定容问题进行了研究，通过对某典型新区的算例进行分析，得到的主要结论如下。

a. 针对电动汽车选址定容问题，提出了一种全社会成本最优化的充电站规划模型，平衡了电动汽车用户、充电站运营方和电网企业的利益。提出了CSAPSO算法来改善粒子群优化算法早熟和局部收敛的问题。

b. 提出的CSAPSO算法相较于传统的粒子群优化算法全局寻优能力更好，求得的规划结果更为优化。通过引入混沌理念，使粒子更加高效地遍历整个搜索空间。同时结合模拟退火算法的概率突跳特性，使算法在迭代进行到中后期时，仍能保持较高的全局寻优能力，避免出现过早的陷入局部最优的情况。

c. 算例中考虑了不同用地性质的情况，并且采用Floyd算法求取距离代替传统算法中的欧氏距离，结合Voronoi图思想及需求点栅格化理论划分充电站服务范围，进一步提高了算法的准确性。

现实中，充电站的选址定容问题仍有很多需要考虑的因素，例如：充电站中快慢桩的配比问题、充电需求的时空分布问题、电动汽车充换电方式等。在下阶段的研究中可以针对以上问题，构建更加合理准确的规划模型。

附录见本刊网络版(http:∥www.epae.cn)。