基于牛顿-欧拉法的人体下肢动力学分析与建模

张玉叶，张原园，毛少坤，张 婷

（咸阳师范学院 物理与电子工程学院，陕西 咸阳 712000）

由于老龄化、疾病、车祸等原因引起中枢系统损伤，产生大量的下肢运动功能障碍患者。依据神经功能重塑理论，运动训练能恢复神经对肢体运动控制，越早及越足量进行训练，恢复效果越好。下肢外骨骼康复机器人作为一种助力设备，可实现实时、有效地提供助力，缓解人体下肢疲劳，这对于老年人与残疾人来说，将是一个福音[1-2]。国外研究机构相继研发了各类康复机器人，如：德国RECK公司研制的MOTOmed康复设备能够实现被动运动、助力运动等功能[3]；美国的RUTGERS大学开展了脚部康复机器人的研究，并研制了RUTGER踝部康复训练机器人；美国密歇根大学研究的下肢康复机器人，实现了肢体的阻抗控制训练[4]。在国内，清华大学、哈尔滨工程大学、西安交通大学等高校也对下肢康复机器人进行了研究。如哈尔滨工程大学开发了卧式下肢康复机器人，对下肢运动障碍的患者进行多模式的康复训练[5]。

由于下肢外骨骼跟随人体下肢一起运动，在理想的情况下，康复机器人通过对穿戴者的运动意图进行“预测”，实时改变外骨骼的运动状态并对驱动关节提供力矩补偿，从而为使用者提供助力[6]。因此，建立合理的人机动力学模型，实时获取人体运动信息，正确判断运动意图，针对这一状况建立机器人动力学模型并进行机器人设计、轨迹规划、动力学优化以及实时控制具有重要的意义。

1 人体下肢的动力学规律及动力学描述

1.1 人体下肢模型及简化

在分析人体下肢运动情况中，把人体简化为质点、质点系、刚体和多刚体系等力学模型，会使研究问题简化。考虑下肢步行在矢状面内的情况，把头和上躯看成一整体，在建模时忽略脚的影响，把脚作为小腿的一部分。这样，简化模型只有5个部分，4个关节的刚体结构，两侧的大腿、小腿和足，均假设为刚体模型，如图1所示。为计算出人体各环节的质量、质心位置和转动惯量，需要直接测量20个人体参数[6]，参考人体肢体参数测量相关文献。动力学一般分析和研究的框图如图2所示。

图1 人体下肢刚体简化模型

1.2 牛顿-欧拉法构建人体下肢动力学模型

动力学是研究物体的运动和作用力之间关系的。现在所用的分析方法很多，有拉格朗日（Lagrange）方法、牛顿-欧拉（Newton-Euler）方法、凯恩（Kane）方法、高斯（Gauss）方法等[7]。牛顿-欧拉法是一种常用的机器人迭代动力学算法，它结合牛顿第二定律和欧拉方程，这种建模方法开放性好，运算步骤相对简洁，计算效率高，并且该方法是非常适合于计算机运算的一种方法，故最终采用牛顿-欧拉法对人体下肢康复机器人进行建模。

刚体的运动等效于质心的平动和绕质心的转动，其中，质心的平动用牛顿方程描述，而绕质心的转动则用欧拉方程定义。牛顿方程和欧拉方程一起，描述了机器人驱动力矩、负载力矩、惯量和加速度之间的关系[8-9]。对于一个刚体，设刚体受到的合力沿x、y、z 3个坐标轴的分量分别为：Fx、Fy、Fz，受到的合力矩沿x、y、z 3个坐标轴的分量分别为：Mx、My、Mz。为了杆件运动，必须加速或者减速它们，运动杆件所需要的力或者力矩是所需速度和杆件质量分布的函数，则刚体的动力学方程可用式（1）表示，关节连接处力简化如图3所示。

图2 动力学研究规律框图

图3 人体连接点力简化图

其中Ix、Iy、Iz表示刚体相对于x轴、y轴和z轴的转动惯量；βx、βy、βz表示刚体相对于x轴、y轴和z轴的角速度；ax、ay、az表示刚体相对于x轴、y轴和z轴的加速度；m表示刚体质量。

2 人体下肢各部分的动力学方程

2.1 踝关节的动力学方程

踝关节实现三自由度的转动，考虑踝关节的坐标系，分析如图4所示，F是地面作用给脚的力，M1是地面作用给脚的力矩，T是踝关节力，M2是踝关节力矩。M3是由踝关节力Tx、Ty相对于脚的质心所产生的力矩。则列写踝关节的动力学方程如式（2）。

其中Iz表示脚对z轴的转动惯量；βz表示脚对z轴的角速度；ax、ay表示脚对x轴、y轴的加速度；m1表示脚的质量。

图4 踝关节受力分析

2.2 骨盆动力学方程的建立

基于牛顿-欧拉法的建模方法，将人体下肢分为四个部分，分别是骨盆、大腿、小腿、脚。其中骨盆有6个自由度，其他的部分均为3个自由度。建立全局坐标系Axyz和局部坐标系 Ax′y′z′，其中局部坐标系固连在骨盆上，如图5所示。则A点、B点和C点在局部坐标系中位置是已知的。可以看到，全局坐标系绕z轴旋转θ角，然后再绕旋转后的坐标系的y轴旋转 β 角，即可得旋转与坐标系 Ax′y′z′的 z′和 y′重合[10-11]。旋转角求解示意图如图6所示，则：

式（3）中，根据前一个等式，方程左侧已知，右侧B点的坐标也已知，故可以求得θ和β。故继而可以求出T。如果人体上身前倾γ角，则C点坐标变化表达式为

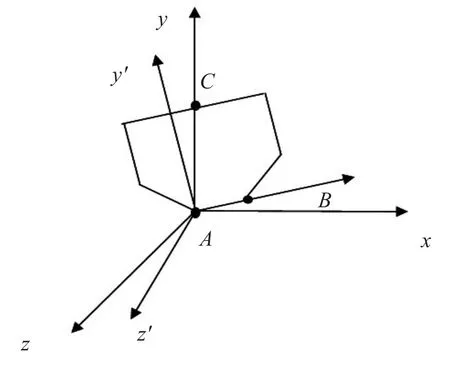
图5 骨盆的全局坐标系与局部坐标系

图6 旋转角速度求解示意图

根据式（4），即可求得C点在全局坐标系下的坐标。那么C点在人体全局坐标系中的坐标为

2.3 骨盆旋转角速度和角加速度的求解

旋转物体上任一点的速度可以用式（6）表示

其中向量r的起始坐标在物体旋转轴上，C点和B点为向量PCB的起止点位置，图6中B点的速度为

B点的速度在坐标系oxy下的表达式为

其中POB为O点到B点的向量，POC为O点到C点的向量。骨盆的角速度和速度关系如式（9），假设D点为在旋转轴上面的任意一点，将每一个向量方程展开为3个标量方程，共9个方程，联立即可求得ω。根据ω，即可求得角加速度。根据以上所述，可以得到骨盆的动力学方程如式（10），各变量的意义参考式（1），m2为盆骨质量。

根据以上所述的分析方法，列出人体下肢各个部分的动力学方程，求解方程，即可得到人体下肢关节的作用力矩。

3 动力学模型仿真

在获得运动学参数的前提下，根据运动学牛顿第二定律和第三定律得到作用于下肢关节的力和力矩。机器人通过对穿戴者的运动意图的正确“预测”，实时改变外骨骼的运动状态并对驱动关节提供力矩补偿，从而为使用者提供助力继而可建立后续的关节驱动力预测模型。

基于正运动学的逆动力学数字计算方法，原理如图7所示。首先给定一个初始的关节角度值，用正运动学计算实时位置，将结果与目标值做对比，用角偏差量修正初始值，如此循环，直到角度误差限定在允许范围内。这样，避免了常规方法中奇异点导致计算失败问题。

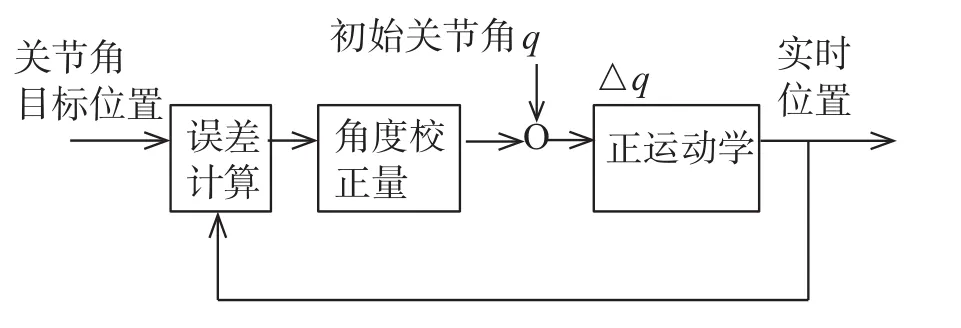
图7 逆动力学数字计算原理

人体下肢从一侧脚跟着地开始到该脚跟再次着地构成一个步态周期。一个步态周期的活动可划分为支撑相和摆动相，常速行走时，支撑相约占整个步态周期的60%～65%，因此，当一侧下肢进入支撑相时，另侧下肢尚未离地，两下肢同时负重称为双肢负重期。双肢负重期约占全周期的28.8%，占支撑相的44.8% ，人体下肢连杆结构的步态模型如图8所示。结合步态特点，人体下肢单腿支撑相和摆动相的下肢各关节力矩曲线仿真结果如图9所示。从关节力矩曲线的变化规律可以看出：

（1）踝关节的关节力矩主要考虑单腿支撑相，在摆动相关节力矩几乎为零。

（2）髋关节的关节力矩主要发生在摆动相，在支撑相惯性力几乎为零。

（3）膝关节的关节力矩在支撑相和摆动相作用相反，各关节广义惯性力主要取决于机器人运动过程中各关节的惯性力大小，受重力的影响较小；仿真曲线验证了该方法的正确性和有效性；可为康复训练机器人人机协同过程中的力学交互模式研究提供参考。

图8 人体下肢连杆结构步态周期图

图9 关节力矩曲线

4 结论

本文用牛顿-欧拉法对人体下肢骨盆（六自由度）、踝关节（三自由度，和膝关节类似）进行了动力学方程的推导，并就其进行了仿真，仿真的结果验证了单腿支撑相和摆动相动力学建模的有效性。这种基于正运动学的逆动力学数字计算方法，避免了常规方法中奇异点导致计算失败问题，因此在下肢康复机器人轨迹规划过程中可以避免奇异点，保护机器人各关节不会因经过奇异点时受到惯性力的破坏。研究方法具有一定的实用性。