基于多目标优化的软件缺陷预测特征选择方法*

陈 翔，沈宇翔，孟少卿，崔展齐，鞠小林，王 赞

1.南通大学 计算机科学与技术学院，江苏 南通 226019

2.桂林电子科技大学 广西可信软件重点实验室，广西 桂林 541004

3.天津大学 信息与网络中心，天津 300072

4.北京信息科技大学 计算机学院，北京 100101

5.天津大学 软件学院，天津 300072

1 引言

开发人员在编码过程中经常会在无意中引入软件缺陷。缺陷产生的原因可能来自于对实际需求的错误理解、不合理的开发过程或开发人员的经验不足等。含有缺陷的软件在部署后可能会产生预期之外的行为，严重的时候甚至会给企业造成巨大的经济损失。因此项目经理希望借助软件测试和代码审查等手段，能够尽可能多地检测出被测项目内的严重缺陷。然而实际的软件测试资源是有限的，因此项目经理希望能够找到有效的方法可以预先识别出可能含有缺陷的程序模块，并对其投入足够的测试资源（例如针对这些模块设计更多的测试用例或进行更为严格的代码审查）。软件缺陷预测（software defect prediction）[1-3]是其中一种有效方法，通过挖掘软件历史仓库（例如版本控制系统、缺陷跟踪系统或开发人员间的电子邮件等）来构建缺陷预测模型，并用该模型来预测出被测项目内的可疑程序模块。

为了更好地进行缺陷预测，研究人员提出了很多与缺陷具有强相关性的度量元（metrics）来对程序模块进行度量。这些度量元一般通过分析代码复杂度和软件开发过程特征来进行设计。从数据挖掘的角度来看，度量元也可以被视为是数据集的特征。但一般来说，并不是所有的特征都有助于构建高质量的模型。具体来说，冗余特征和无关特征的存在会提高模型的构建时间，甚至有时会降低模型的预测效果。该问题又被称为维数灾难问题。因此设计出新颖有效的特征选择方法具有重要的研究意义和价值。除此之外，更少的特征还有助于提高模型的可解释性和模型的可视化。

Harman等人[4-5]认为基于搜索的软件工程方法（尤其是多目标优化方法）可以在软件工作量估算、软件缺陷预测或性能预测等研究问题上取得成功。虽然近些年来研究人员尝试将特征选择应用于软件缺陷预测领域并取得了一些研究成果[6-15]，但是研究人员考虑的特征选择方法都是基于单目标优化的，目前尚未有研究人员将软件缺陷预测特征选择问题建模为多目标优化问题并展开深入研究，因此本文从这个角度入手尝试提高缺陷预测模型的预测效果，具体来说，主要考虑两个优化目标，一个目标从成本分析角度出发，尝试最小化选出的特征数；另一个目标从收益分析角度出发，尝试最大化缺陷预测模型的预测效果。随后本文提出了MOFES（multiobjective optimization feature selection）方法来平衡这两个潜在矛盾优化目标。为了验证本文所提方法的有效性，选择了来自实际开源项目的PROMISE和RELINK数据集作为评测对象，使用k近邻法来构建模型，使用AUC评测指标来度量模型的预测效果。与一些经典的基准方法（例如FULL、SOFS、GFS和GBS）进行对比，发现：（1）在大部分情况下，MOFES方法可以更为有效地探索搜索空间，最终可以选出规模更小的特征子集，并且同时可以获取更好的预测效果。（2）MOFES的计算开销要超过GFS方法和GBS方法，但要少于SOFS方法，总体来看，MOFES方法的计算开销在可接受的范围之内。

本文的主要贡献总结如下：

（1）将软件缺陷预测特征选择问题建模为多目标优化问题，提出一种基于多目标优化的包裹式软件缺陷预测特征选择方法MOFES，其尝试最小化选出的特征数及最大化构建出的缺陷预测模型性能。

（2）在来自实际开源项目的两组数据集上进行实证研究，来验证MOFES方法的有效性。这两组数据集考虑的度量元和分析的开源项目均不相同，因此可以确保实证研究结论具有一般性。最终结果表明多目标优化方法在软件缺陷预测特征选择问题上具有一定的优势。

2 研究背景和相关工作

软件缺陷预测[1-3,16-18]是当前软件工程数据挖掘领域中的一个研究热点。其主要包含两个阶段：模型构建阶段和模型应用阶段[3]。具体来说，模型构建阶段会首先挖掘软件历史仓库来抽取程序模块并对其进行标记（即标记为有缺陷模块或无缺陷模块）。其中程序模块粒度可根据实际需要，将其设置为文件、类或代码修改等。随后通过分析代码复杂度或软件开发过程，设计出与缺陷存在相关性的度量元来对抽取出的模块进行度量。基于上述步骤，可以构造出缺陷预测数据集并选择特定的分类器（例如决策树、k近邻法等）来构建出缺陷预测模型。在模型应用阶段，可以使用构建出的模型来预测出被测项目内的可疑缺陷模块。具体过程如图1所示。

若考虑多种度量元，则搜集的缺陷预测数据集内可能会存在维数灾难问题[11-13]。假设数据集含有n个特征，则所有可能的特征子集数为2n。因此当n值增大时，其搜索空间规模将呈指数级增长。其次特征之间的交互关系较为复杂，例如：一个特征可能跟类标之间的相关度不高，但如果与其他具有互补关系的特征相结合构成特征子集，则可能会提高随后构建的模型性能。或者一个特征可能跟类标之间的相关度很高，但如果与其他特征相结合构成特征子集，则该特征可能会成为冗余特征。特征选择是缓解维数灾难问题的一种有效方法，其尝试尽可能多地识别并移除已有特征集中的无关特征和冗余特征。其中无关特征与类标的相关性较低，而冗余特征则会含有其他特征含有的信息。已有的特征选择方法可以简单分为两类：包裹式方法和过滤式方法。其中包裹式方法需要借助指定的建模方法来评估选出的特征子集的质量，而过滤式方法则仅借助数据集的特征来评估选出的特征子集的质量。因此后一类方法的计算开销较小，但预测效果难以保障[19]。

Fig.1 Process of software defect prediction图1 软件缺陷预测流程

近些年来，研究人员尝试借助特征选择来提高缺陷预测模型的性能。大部分研究人员考虑的是过滤式方法。Menzies等人[6]考虑了基于信息增益的特征选择方法，主要考虑了前向搜索和穷尽搜索策略。Gao等人[7]在大规模遗留软件系统上考虑了特征选择方法，他们考虑了不同的特征排序和子集评估策略。Wang等人[8]借助集成学习来提高特征选择的性能。Liu等人[11]提出一种基于特征聚类和特征排序的特征选择框架FECAR，随后Liu等人[12]提出一种两阶段数据集预处理方法，其同时考虑了特征选择和实例选择。最后发现数据集中的噪音是难以彻底移除的，因此Liu等人[13]提出具有一定噪音容忍能力的特征选择框架FECS。与FECAR相似，Xu等人[14]同样提出一种基于聚类分析的特征选择方法MICHAC（defect prediction via maximal information coefficient with hierarchical agglomerative clustering）。Shivaji等人[10]在基于代码修改的缺陷预测[20]中考虑了不同的特征选择方法。考虑包裹式特征选择方法的研究工作相对较少，Song等人[9]在他们的通用缺陷预测框架中考虑了包裹式特征选择方法。Xu等人[15]分析了32种不同的特征选择方法，这些方法被分为5类（过滤式特征排序方法、过滤式子集选择方法、包裹式子集选择方法、基于聚类的方法、基于抽取的方法）。在大规模实证研究中，他们发现在不同数据集上，不同方法之间基于预测效果的排序并不一致。

基于相关工作分析发现虽然研究人员对软件缺陷预测特征选择的研究已经取得了一定的研究进展，但并未有研究人员将该问题建模为多目标优化问题。虽然Canfora等人[21]曾经将多目标优化应用到软件缺陷预测中，但本文工作与他们工作的不同之处有两点：首先关注的问题不同，Canfora等人关注的是跨项目缺陷预测问题，重点关注的是缺陷预测特征选择问题。其次关注的优化目标不同，他们尝试借助多目标优化方法在识别出的缺陷模块数和需要的代码审查量之间进行折衷选择。而本文尝试借助多目标优化方法在选出的特征子集规模和随后构建出的缺陷预测模型性能之间进行折衷选择。

3 MOFES方法

本文属于基于搜索的软件工程（search based software engineering，SBSE）[4]研究领域。SBSE的概念最早由Mark Harman提出并逐渐成为软件工程领域的一个研究热点。目前已经逐渐应用到软件开发生命周期的各个阶段，从需求分析、软件设计、软件测试到软件维护等。SBSE之所以受到很多研究人员的关注，是因为其提供了自动化或半自动化的解决方案，有助于在拥有大规模搜索空间的复杂软件工程问题中找到高质量解。Harman[5]同样认为SBSE（尤其是多目标优化方法）可以用于辅助构建高质量的缺陷预测模型。

针对软件缺陷预测特征选择问题，定义了两个优化目标，其中一个优化目标从问题的成本角度出发，希望能够尽可能减少需要选出的特征数，另一个优化目标从问题的收益角度出发，希望能够尽可能多地提高缺陷预测模型的预测效果。不难看出，大部分情况下这两种优化目标存在明显的矛盾。具体来说，若希望选出的特征数越少，则可能会降低随后构建出的模型预测效果。相反若希望提高随后构建出的模型预测效果，则可能需要选出更多的特征。因此希望借助多目标优化方法在这两个潜在矛盾的优化目标中进行折衷，并设计出MOFES方法。借助该方法，可以获得一系列具有非支配关系的特征子集，并且可以根据偏好（例如倾向于选出更少的特征数或倾向于构造出更高预测效果的模型）从中选出实际需要的特征子集。

为了方便随后的描述，首先给出与多目标优化相关的定义。

定义1（Pareto支配关系）假设wi和wj是缺陷预测特征选择问题的两个可行解，称wiPareto支配wj，当且仅当：

在该问题中，可行解表示某个特征子集，benefit函数返回使用该特征子集后构建出的模型预测效果，cost函数返回的是该特征子集的规模。

定义2（Pareto最优解）一个可行解w是Pareto最优解，当且仅当不存在任何可行解w*，可以Pareto支配w。

定义3（Pareto最优解集）该集合包含可行解中所有的Pareto最优解。

使用一个虚拟实例来阐述上述定义。假设MOFES方法生成了7个可行解，如图2所示。其中x坐标轴表示可行解对应的特征数（即cost目标），y坐标轴表示可行解基于选定特征构建出的模型预测性能（即benefit目标）。不难看出可行解BPareto支配可行解E，因为benefit(B)＞benefit(E)并且cost(B)≤cost(E)。同时可行解A、B、C和D均是Pareto最优解并构成了Pareto最优解集，在图2中，不存在其他可行解，可以Pareto支配这些解。

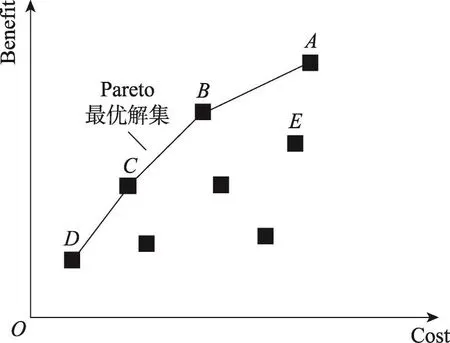
Fig.2 Interpretation for definitions in multi-objective optimization图2 对多目标优化中定义的解释

研究人员提出了多种不同的演化多目标优化算法，这些算法借助演化算法来尝试构造出Pareto最优解集。本文提出的MOFES主要基于一种经典的演化多目标优化算法NSGA-Ⅱ[22]，NSGA-II算法在每次种群演化时，首先借助演化算子生成新的染色体，随后将这些染色体与上一轮种群的染色体合并，接着进行基于分层的快速非支配排序，同时对于每个非支配层中的染色体进行拥挤度计算，最后根据非支配关系以及染色体的拥挤度，选择合适的染色体组成新的种群。其中基于分层的非支配排序、拥挤度计算以及精英保留机制均可以有效避免种群的过早收敛问题。其整体框架如算法1所示。

算法1MOFES

输入：种群规模N，最大迭代次数T。

输出：Pareto最优解集。

首先介绍染色体的编码方案，针对该问题，若数据集有n个特征，则染色体可以用n比特串来表示。假如第i个比特取值为1，则表示对应的第i个特征被选入，若取值为0，则表示对应的第i个特征未被选入。假设数据集考虑了5个特征{f1,f2,f3,f4,f5}，并且初始种群为{10010,00100,10110}。这表明该初始种群包含3个染色体，其对应的特征子集分别为{f1,f4}、{f3}和{f1,f3,f4}。

算法1首先使用步骤2中的initPop函数来初始化种群，其中种群规模为N，种群中每个染色体随机生成。针对软件缺陷预测特征选择问题，有3种启发式种群初始化策略：small初始化策略、large初始化策略和hybrid初始化策略。其中在small初始化策略中，种群中的每个染色体随机选出的特征数小于原有特征数的一半。在large初始化策略中，种群中的每个染色体随机选出的特征数大于原有特征数的一半。在hybrid初始化策略中，一半的染色体采用small初始化策略，另一半染色体使用large初始化策略。在MOFES方法中small初始化策略更为有效。

随后MOFES在步骤4中使用makeNewPop函数，借助演化算子（例如交叉算子、变异算子）来生成新的染色体。具体来说，交叉算子会根据交叉概率随机选出两个染色体，进行交叉并生成两个新的染色体，变异算子会根据变异概率随机选出一个染色体，进行变异并生成一个新的染色体。

接着MOFES通过步骤5到步骤16，借助选择算子从已有染色体中选出更高质量（基于Pareto支配关系分析）的染色体到下一轮种群中。具体来说，首先将原有的染色体和借助变异算子和交叉算子生成的新染色体合并到集合Bi中。然后使用fastNondominated-Sort函数来为Bi中的每个染色体算出NDR（nondominated rank）值。具体来说，首先从Bi中识别出所有不被Pareto支配的染色体，将他们的NDR值设置为1，并将它们从集合Bi中移到集合F1。随后继续从Bi中识别出所有不被Pareto支配的染色体，将它们的NDR值设置为2，并将它们从集合Bi中移到集合F2。重复执行上述过程，直至集合Bi为空。基于染色体的NDR值，会尽力选择NDR值更小的染色体到下一轮种群中。在步骤14中，使用了拥挤距离（crowding distance）[21]的概念，通过拥挤距离可以避免选出具有高相似度的染色体。

当达到最大迭代次数后，MOFES方法满足终止条件并返回当前种群中的所有Pareto最优解。

4 实证研究

4.1 评测对象

为了验证MOFES方法的有效性，本文选择了PROMISE和RELINK数据集作为评测对象。这些数据集中共涉及了13个开源项目，累计共有5 757个程序模块。这些开源项目处于不同类型领域，例如Ant是Java程序的构建程序，Lucene是搜索引擎工具包。除此之外，这两个数据集也分别考虑了不同类型的度量元。因此不难看出，本文选择的评测对象具有一定的代表性。

PROMISE数据集由Jureczko和Madeyski[23]搜集完成，其主要来自10个不同的开源项目（例如Ant、Lucene、Poi等）。他们将程序模块的粒度设置为类，并考虑了20种度量元，这些度量元考虑了面向对象程序中的封装、继承和多态等特征。PROMISE数据集的统计信息（包括项目名称、模块粒度、模块数以及缺陷模块数）如表1所示。

RELINK数据集由Wu等人[24]搜集，他们分析的开源项目是Apache HTTPServer、Safe和ZXing。该数据集共考虑了26种度量元，这些度量元均关注的是代码复杂度，并借助Understand工具进行搜集。他们随后通过手工验证和校对等方式进一步提高了数据集的质量。RELINK数据集的统计信息（包括项目名称、模块粒度、模块数以及缺陷模块数）如表2所示。

4.2 模型预测效果评测指标

本文使用AUC（area under the ROC curve）指标来评估缺陷预测模型的预测效果。其中AUC值为ROC曲线下的面积，其取值越接近于1，表示对应的模型的预测效果越好。使用ROC曲线可以考虑不同的阈值，其中水平坐标轴表示TPR（true positive rate）值，垂直坐标轴表示FPR（false positive rate）值。根据不同的阈值，模型会具有不同的TPR值和FPR值并对应为坐标上的一个点，将所有点进行连接就可以形成ROC曲线。因此与传统查准率、查全率、F1指标相比，AUC指标更适用于具有类不平衡问题的软件缺陷预测研究[15]。

Table 1 Characteristics of PROMISE datasets表1PROMISE数据集的统计信息

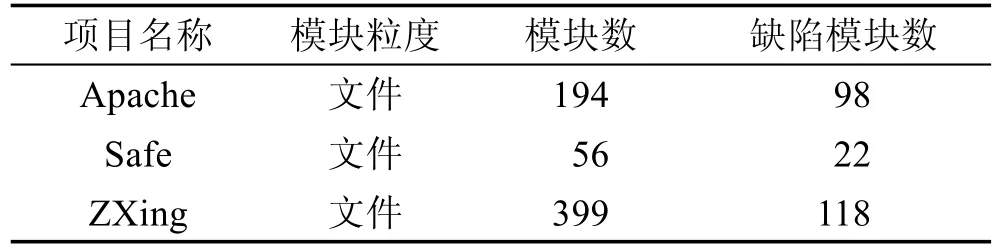
Table 2 Characteristics of RELINK datasets表2RELINK数据集的统计信息

4.3 实验设计

为验证MOFES方法的有效性，考虑了4种基准方法。

（1）第1种基准方法不进行特征选择，即使用原有的特征来构建模型，本文将该方法称为FULL方法。

（2）第2种基准方法是基于单目标优化的包裹式特征选择方法，与MOFES不同之处在于该方法仅优化单一目标（即模型的预测效果）。本文将该方法称为SOFS方法。

（3）第3种基准方法和第4种基准方法是基于贪心前向搜索和贪心后向搜索的包裹式特征选择方法。本文将这两种方法分别称为GFS方法和GBS方法。Song等人[9]在他们提出的通用软件缺陷预测框架中考虑了这两种特征选择方法。具体来说，GFS方法会从空集开始（即不包含任何特征），借助爬山法每次添加一个最优特征，直至模型的预测效果不能得到提升为止。GBS方法会从原有特征集开始，借助爬山法每次移除一个特征，直至模型的预测效果不能得到提升为止。上述两种方法均存在嵌套效应，即一旦一个特征被添加（或移除），其在后续迭代过程中，就不会被移除（或添加），该问题会使得这两种方法在搜索时容易陷入局部最优。

这里需要注意的是本文重点研究的是包裹式特征选择方法，因此在选择基准方法的时候并未考虑在相关工作中提到的过滤式特征选择方法。

当完成特征选择后，使用k近邻法来构建缺陷预测模型。k近邻法的建模质量与选出的特征质量密切相关，选出更好的特征将有助于更为精准地计算出程序模块间的相似度，从而更好完成对软件模块的缺陷预测。基于特征选择的模型性能评估过程如图3所示：首先使用分层采样来分别构建训练集和测试集，即选择70%的实例来构成训练集，而用剩余30%的实例来构成测试集，借助分层采样可以保证训练集和测试集中不同类型的实例分布保持一致。在测试集上借助MOFES方法生成Pareto最优解集，对于集合中的每个Pareto最优解，会根据其选中的特征子集同时对训练集和测试集进行数据预处理，在预处理后的训练集上借助k近邻法构建模型，并将模型应用于测试集上并得到该特征子集对应的模型预测效果。为了在测试集上评估每个染色体（即特征子集）的适应值，进一步在测试集上使用3折交叉验证，即首先将测试集上的数据借助分层采样方法将之划分为3组，每次用两组数据根据染色体对应的特征子集进行数据预处理，借助k近邻法构建模型，并用剩余1组的数据来评估该模型的性能，重复3次（即确保每个实例都被预测过1次），并取这3次性能的均值作为该染色体的适应值。

Fig.3 Process of model performance evaluation图3 模型预测效果的评估过程

MOFES方法和SOFS方法中的参数名称和具体取值如表3所示，包括种群规模、最大迭代次数、交叉概率和变异概率。增加最大迭代次数可能会选出质量更高的特征子集，并提高随后构建出的模型预测效果，但也会大幅度提高特征选择方法的执行时间开销。在实证研究中，根据实际执行效果和多目标优化算法在数值问题求解中的建议取值[25]确定了表3所示的参数取值。

Table 3 Name of parameters and their value used in MOFES表3 MOFES方法中使用的参数名称和取值

MOFES方法和所有基准方法均借助Weka软件包编程实现，并统一运行在Win 10操作系统（Intel i7-3612QM CPU，8 GB内存）。

4.4 结果分析

4.4.1 模型预测效果比较

本节主要从模型预测效果角度将MOFES方法与基准方法进行比较。由于MOFES方法和一些基准方法内存在随机因素，因此独立运行这些方法10次。基于PROMISE和RELINK数据集的结果分别如图4和图5所示。在每个子图中，项目名称后的括号内包含原有特征数以及未进行特征选择（即使用FULL方法）时构建的模型预测效果。例如：Camel-1.6后括号内的内容为（20，0.6），这表示原有的特征数为20，未进行特征选择时的模型预测效果为0.6（基于AUC评测指标）。在每个子图中，横坐标表示不同方法选出的特征数，纵坐标表示使用该特征子集构建出的模型预测效果。SOFS、GFS和GBS均会独立执行10次，但可能会在不同执行过程中选出相同的特征子集，因此在一些子图中可能会出现实际点的数量少于10的情况。除此之外，MOFES方法基于测试集上的执行结果也会产生10个不同的Pareto最优解集。用两种方式表示MOFES方法的执行结果。首先将这10个不同Pareto最优解集中的解合并到一个集合T，第一种方式将集合T中具有相同特征子集规模的解合并到同一组，并计算出模型性能的均值（因为相同的特征子集规模并不一定代表选出相同的特征），其用MOFES-A折线表示。第二种方式会从T中进一步找出Pareto最优解集并返回，其用MOFES-B折线表示。

首先将MOFES、SOFS、GFS和GBS这4种方法与FULL方法进行比较，通过2个数据集的13个项目发现借助特征选择，总存在一些方法可以找出一些特征子集，其随后构建出的模型预测效果要优于使用原有特征集构建的模型预测效果。以Camel-1.6为例，其使用原有特征集构建出的模型预测效果为0.604（基于AUC评测指标）。借助GBS方法，其最好的结果是通过选出17个特征，其模型预测效果可达到0.647。借助GFS方法，其最好的结果是通过选出6个特征，其模型预测效果可达到0.66。借助SOFS方法，其最好的结果是通过选出10个特征，其模型预测效果可达到0.677。而本文所提的MOFES方法，其最好的结果是通过选出4个特征，其模型预测效果可达到0.711。这些结果均超过0.604。同时MOFES方法在这个项目中可以选出更少的特征，并达到最好的预测效果。

其次分析MOFES、SOFS、GFS和GBS这4种方法选出的特征数，不难看出GFS方法选出的特征子集规模最小，GBS方法选出的特征子集规模更大，SOFS选出的特征子集规模介于两者之间，而本文所提的MOFES方法，由于每次返回的是Pareto最优解集，其选出的特征子集规模分布较广，因此在选择的时候具有更强的灵活性。

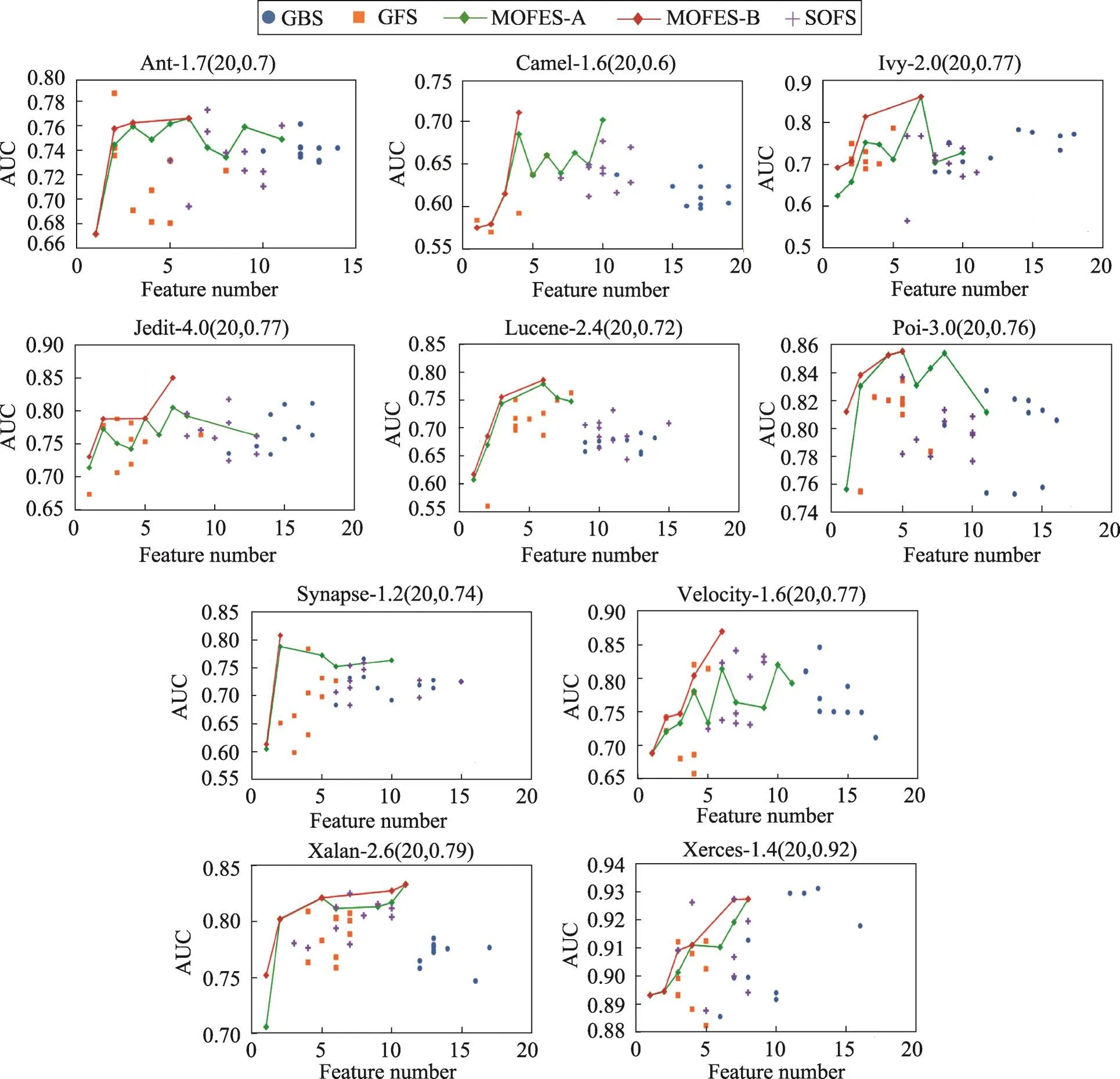
Fig.4 Prediction performance comparison of different methods for PROMISE datasets图4 不同特征选择方法在PROMISE数据集上的结果

接着给出MOFES、SOFS、GFS和GBS这4种方法在10次独立执行后可以取得的最好模型预测效果。其中基于PROMISE数据集的结果如表4所示，基于RELINK数据集的结果如表5所示，其中括号内表示对应选出的特征子集规模，对每个项目上的最好结果进行了加粗，每个表的最后一行显示的是在数据集所有项目上的均值。不难看出，除了在Ant-1.7和Xerces-1.4，MOFES总能获得最好的预测效果。进一步将MOFES方法与单目标特征选择方法SOFS进行对比，MOFES方法在大部分情况下，可以在获得更好的预测效果时，选出的特征数更少（除了Xalan-2.6、Xerces-1.4和 ZXing）。总体来说，基于PROMISE数据集的均值分析，MOFES相对SOFS、GFS和GBS来讲，其模型预测效果分别有3.37%、4.16%和5.35%的提升。基于RELINK数据集的均值分析，MOFES相对SOFS、GFS和GBS来讲，其模型预测效果分别有5.19%、4.50%和9.27%的提升。

Fig.5 Prediction performance comparison of different methods for RELINK datasets图5 不同特征选择方法在RELINK数据集上的结果

Table 4 Best result of different methods for PROMISE datasets表4 不同特征选择方法在PROMISE数据集上的最好结果

因此与单目标优化方法相比，借助多目标优化方法可以更为有效地探索搜索空间，并找出质量更高的特征子集。除此之外基于图4和图5中的MOFES-B，在选出的特征数和模型的预测效果上存在明显的折衷，这也验证了这两个优化目标存在一定的冲突性。以Ant-1.7为例，其MOFES-B折线对应4个解，分别是解A（1，0.672）、解B（2，0.758）、解C（3，0.763）和解D（6，0.766）。不难看出这4个解构成了Pareto最优解集。若选择特征数较少的解（例如解A），其随后构建的模型预测效果为0.672，要弱于选择特征数较多的解（例如解D）随后构建的模型预测效果（0.766）。

综上所述，在两组数据集的13个项目中，MOFES方法在其中11个项目上可以选出更高质量的特征子集并获取更好的模型预测效果。

4.4.2 执行时间开销比较

本节主要将MOFES方法的执行时间开销与其他基准方法进行比较。搜集了每个特征选择方法独立运行10次的时间总和。其中基于PROMISE数据集的运行时间结果如表6所示，基于RELINK数据集的执行时间结果如表7所示。基于PROMISE数据集，MOFES方法的执行时间是GFS方法的14.13～25.61倍，是GBS方法的4.86～8.82倍，但仅是SOFS方法的0.77～0.85倍。基于RELINK数据集，MOFES方法的执行时间是GFS方法的11.46～12.85倍，是GBS方法的4.47～6.62倍，但仅是SOFS方法的0.81～0.88倍。

Table 6 Computational cost of different methods for PROMISE datasets表6 基于PROMISE数据集的运行时间 s

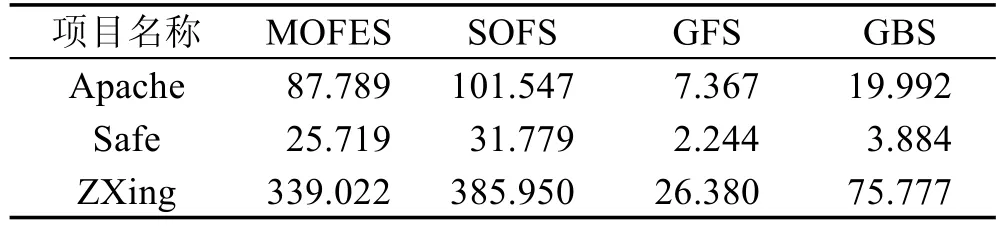
Table 7 Computational cost of different methods for RELINK datasets表7 基于RELINK数据集的运行时间 s

综上所示，MOFES方法运行时间要超过GFS方法和GBS方法，但要少于SOFS方法，并且总体来看其计算开销是可接受的。例如在PROMISE数据集中，MOFES方法的执行时间最多是1 205.109 s。在RELINK数据集中，MOFES方法的执行时间最多是339.022 s。同时在模型预测效果比较时，MOFES方法虽然需要花费一定的时间进行特征选择，但在大部分情况都能训练出预测效果更好的缺陷预测模型。

4.4.3 MOFES选出的特征统计

本节主要分析MOFES方法经常选出的特征，其分析结果有助于选出最有价值的特征来指导缺陷预测数据集的搜集。

由于MOFES方法在每个数据集上均会独立运行10次，每次会获得一个Pareto最优解集。因此基于10组Pareto最优解集，可以算出每个特征的被选频率。假设针对项目d，其10组Pareto最优解集中共含有100个解，其中60个解含有特征fi，则特征fi的被选频率为60%。以PROMISE数据集为例，该数据集含有10个项目，因此针对每个特征会有10个被选频率，在特征排序时，首先按照10个被选频率的中位数进行排序，若中位数取值相等，则进一步按照均值进行排序。基于PROMISE数据集和RELINK数据集的最终结果如表8所示，其特征具体含义可参考对应文献[22-23]。

4.5 有效性影响因素分析

本节简要讨论可能影响到实证研究结论有效性的一些影响因素。外部有效性主要涉及到实证研究得到的结论是否具有一般性。为避免该影响因素，本文选择了软件缺陷预测研究中经常使用的评测数据集PROMISE和RELINK[18,21,23-24]。这些数据集共含有5 757个程序模块，涉及到13个不同类型的开源项目，因此可以确保研究结论具有一定的代表性。除此之外，本文对缺陷预测研究中使用较多的其他数据集（例如NASA、Softlab等）也进行了验证并得到了相似结论。内部有效性主要涉及到可能影响到实证研究结果正确性的内部因素。为避免该影响因素，本文在实现方法时主要基于Weka软件包，因此可以最大程度保证分类器和一些基准特征选择方法实现的正确性，除此之外，还通过一些简单实例对MOFES方法的正确性进行了验证。构造有效性主要涉及到使用的评测指标是否合理。因为数据集内存在类不平衡问题，为避免该影响因素，使用了AUC评测指标。

Table 8 5 features with the highest selected frequency表8 被选频率最高的5个特征

5 结束语

目前多目标优化在软件缺陷预测问题中的应用并不多，本文将软件缺陷预测特征选择方法建模为多目标优化问题，并提出了MOFES方法。基于来自实际开源项目的PROMISE数据集和RELINK数据集验证了MOFES方法的有效性。

在下一步工作中，首先将尝试基于更多实际项目（尤其是来自商业项目）的数据集来验证本文所提方法的有效性。其次尝试考虑其他多目标优化算法（例如SPEA[26]、基于粒子群优化的SMPSO等[27]）来丰富MOFES方法，并采取合适的指标（例如hypervolume）来评估不同多目标优化算法生成的Pareto最优解集的质量。接着尝试考虑更多的分类器（例如决策树、朴素贝叶斯、集成学习等）来分析MOFES方法是否会受到分类方法的影响。然后尝试通过寻找最优参数取值以及设计更为有效的演化算子来优化MOFES方法。最后本文所考虑的PROMISE数据集和RELINK数据集的度量元介于20～30之间，若研究人员考虑更多的度量元，则本文所提的MOFES方法会存在计算开销过大的问题，这时候将进一步针对软件缺陷预测特征选择问题研究基于多目标优化的过滤式特征选择方法。