电涡流传感器探头线圈交流电阻受温度影响*

2018-09-11罗茹丹李中秀

传感器与微系统 2018年9期

罗茹丹，吴峻，李中秀

(国防科技大学智能科学学院，湖南长沙 410073)

0 引言

电涡流传感器线圈的阻抗变化在一定条件下可以反映线圈到被测导体间的距离[1]。但在实际应用中，等效阻抗的实部—交流电阻值比较容易受环境温度波动的影响而使线圈阻抗值不能成为线圈到被测金属导体距离的单值函数，因此,如何消除温度变化对交流电阻值的影响一直是国内外学者针对电涡流传感器实际应用的一个讨论热点。

通过求解电涡流传感器探头和被测导体间的电磁场分布来计算阻抗是一种常用方法，但其涉及积分方程的求解，理论求解难度较大。文献[2]通过分别建立激励线圈、涡流环以及互感计算模型，利用经验公式对交流电阻值进行计算，其计算理论值与实测值间的误差较大，需设计修正函数进行补偿；文献[3]将线圈阻抗的积分表达式转换为级数表达式后利用MathematicTM计算，避免了贝塞尔函数的双重积分使得求解速度大幅提高;文献[4]利用一种多变压器模型等效电涡流传感器模型，通过求解电压方程组来求解交流电阻值，该方法只涉及线性交流电路分析和椭圆积分，易于实现;文献[5]分析了温度的变化因线圈导线集肤效应对交流电阻值的影响，提出采用多股细辫线代替单匝粗导线的方法减弱温度对交流电阻值的影响；文献[6,7]从电阻率和电流密度分布2个角度分析交流电阻值受温度的影响情况，提出通过改变探头线圈的材料、尺寸等参数来抑制温度的影响，其对交流电阻值的温度影响分析是针对探头线圈本身，忽略了处在同一温度变化下的被测导体对其的影响。

本文针对文献[4]提出的多变压器模型根据高频反射式电涡流传感器的特点进行简化，在保证计算有效性的基础上减轻了计算工作量。并在文献[6]分析的基础上考虑线圈与被测导体之间的磁性耦合关系，讨论被测导体受温度影响而对交流电阻值产生的影响，比较完善地分析了交流电阻值受温度的影响情况。同时利用Maxwell涡流场建立电涡流传感器探头线圈模型进行仿真验证。

1 电涡流传感器探头线圈模型简化

当其他参数不变时，电涡流传感器的输出与其等效阻抗值一一对应，建立阻抗矩阵进行等效阻抗计算是一种比较有效的计算方法。如图 1所示，将电涡流传感器的整个探头线圈分解为以单个圆环线圈为元素的集合，将被测材料中电涡流分布区域同时沿轴向与径向分解为以单元涡流回路为元素的集合，通过计算所有单元线圈、单元涡流间的自互感，建立并求解包括所有单元线圈回路与单元涡流回路间的电压方程组，最终得到探头线圈输出阻抗数值[4]。

图1 等效多变压器模型

图1中h，r，w，c，a分别为探头线圈与被测导体的尺寸；p，q，k，s分别为划分探头线圈与被测导体单元的方向；d为两者之间的距离，(pt,qt)和(kv,sv)分别为探头线圈和被测材料的一个划分单元，R，L，M分别为电阻值、电感值和互感值。

该模型可以较为准确地计算出交流电阻值，但针对一些激励频率设定比较高或者被测材料电导率比较高的电涡流传感器，可简化该模型，不影响求解的准确性。

2 温度对交流电阻值的影响

1)温度影响导体材料的电磁特性：当环境温度发生波动时，探头线圈中金属导体自身的电导率会发生变化，由于金属导电材料多采用铜、银等非磁性金属材料，其相对磁导率接近1，可以视为不受温度变化的影响。

2)温度影响探头线圈的几何尺寸：在不同的温度下，线圈会根据热胀冷缩的原理而发生几何尺寸的改变，不过根据线圈材料的特性，只有在温度大幅度的变化下才会发生比较明显的影响，因此，一般的工作环境的温度波动对此的影响可以忽略。

探头中的线圈实质上是一个空心电感线圈，其等效复阻抗可表达为[9]

(1)

式中R为等效电阻值，L为等效电感值，ω为激励电流的角频率，μ0为真空导磁率，W为线圈的匝数，d为线圈的平均直径，φ为由矩形线圈截面的宽度r、高度h和线圈平均直径d决定的参数。

与线圈电感值相关的参数几乎不受温度影响，故交流阻抗随温度的变化主要体现在交流电阻值受温度的影响。

由文献[10]欧姆损耗计算式可知电涡流传感器探头线圈的趋肤深度与线径大小:

1)线径比较小，小于等于趋肤深度时，趋肤深度和邻近效应的影响可以忽略不计，即交流电阻值与直流电阻值差别不大，则温度对交流电阻值的影响主要体现在电阻率的变化上[11]，两者关系为

(2)

式中R为电阻值，t为温度，ρt0为t0温度下的线圈材料的电阻率,a为t0温度下的温度系数,L为线圈长度,S为线圈截面积。

2)线径大于趋附深度时，需要考虑趋附深度和邻近效应，交流电阻值的影响主要体现在两个方面[6]：

a.受集肤效应影响，交流电阻值可由式(3)计算，且温度对交流电阻值的影响正相关

(3)

式中f为电流频率，μ0为真空磁导率，μr为相对磁导率，Rdc为直流电阻值，由式(2)计算。

b．温度的升高使得金属导体的电阻率增大，导致集肤效应能力减弱，集肤深度增大，导线中电流密度的分布愈均匀，这种影响使得等效交流电阻值随温度升高而变小，即

(4)

式中Jot为t℃时的电流密度,U为激励电压。

此外，由于被测材料经常选用导磁性金属材料，因此其电导率和磁导率都会受温度影响而发生变化，根据电涡流传感器的基本检测原理可知，交流电阻值与被测材料感应短路环电阻值存在以下关系

(5)

式中R为交流电阻值,R1为传感器线圈电阻值,ω为电流频率,M为互感值,R2,L2分别为被测材料电阻值和电感值。

温度的升高会同时影响被测材料磁导率的降低和电阻率的升高，磁导率的降低导致被测材料中感应的涡流变小，即两者间的磁性耦合关系也相应变弱，相当于式(5)中M值的降低，而被测材料电阻率的升高则导致被测材料的电阻值变大，即R2值变大，根据导磁性金属材料的属性，在一定温度范围内，电阻率受温度的影响远大于磁导率受温度的影响，由此可推出温度的升高影响交流电阻值变大。

3 仿真与分析计算

以测量量程为2 mm的高频反射式电涡流传感器探头线圈(145匝铜材料)为例，其仿真模型如图2所示。

图2 线圈仿真模型示意

被测导体的材料为钢，假设其长、宽和厚度都无限大，仿真电涡流传感器探头线圈线径为0.135 mm，远大于趋肤深度0.003 17 mm(激励频率为500 kHz)，可利用简化的多变压器模型进行计算，建立对应的阻抗矩阵和电压方程组，仿真得到不同频率情况下的交流电阻值情况，如图3所示。

图3 不同频率下交流电阻值计算结果

由仿真结果可知，交流电阻值与线圈和钢板之间距离呈负相关，激励电流频率越大，交流电阻值越大，不同频率下，交流电阻值随距离变化趋势基本一致。

分别利用未简化和简化的多变压器模型进行仿真，通入激励电流的频率为500 kHz，计算结果如图 4所示。简化的多变压器模型与未简化的模型计算结果几乎完全重合，证明提出的简化多变压器模型正确有效。

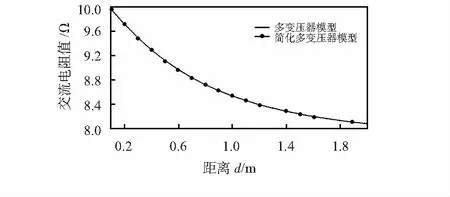
图4 简化多变压器模型验证

在Maxwell涡流场里建立电涡流传感器探头线圈模型进行仿真，模型与参数如图2。主要通过同时改变线圈和被测导体材料的电阻率来表现电涡流传感器工作环境温度的变化，固定线圈与被测导体距离d为0.8 mm，仿真不同频率下交流电阻值受温度影响的变化，如图 5所示。仿真结果显示交流电阻值随温度的升高而增大，激励频率越高对应交流电阻值越大，但其变化规律受频率的影响较小。由此也可以得出，前文所述交流电阻值受温度的影响受电流密度分布影响较小。