基于驻站和限流的组合公交控制策略研究

黄青霞，贾 斌*，强生杰，肖 尧

(1.北京交通大学 交通运输学院，北京100044；2.华东交通大学 交通运输与物流学院，南昌330013)

0 引言

面对日渐严峻的城市交通拥堵问题，国家大力号召发展公共交通，以提高道路资源的利用率.但在实际的路面公交运营中，难以预测的道路干扰及站点之间巨大的客流量差异往往会破坏公交车辆的稳定运行，造成2辆或更多车辆在视线范围内共同运行或同时进站的现象，即公交串车.公交串行是一种非正常的公交运行状态，它会增加部分乘客的等待时间、加剧车辆载客量不均匀问题，导致公交吸引力下降.

为了有效解决串车问题以提高公共交通的缓堵能力，交通研究者在公交控制策略方面投入了大量的工作，常用的策略有驻站、跳站和公交信号优先等.现有研究组合多种策略，扬长避短，以期得到更为有效、适用且负面影响较小的公交调度方案[1].在考虑信号灯影响的线路中，学者们借助驻站—信号优先混合策略，强制早到车辆停滞一段时间再发车，使晚到公交车优先通过信号交叉口.马万经等[2]求解了一种最小化公交延误偏差的混合控制模式，王宁等[3]提出了应用于城市快速公交的调度方法.不考虑信号交叉口时，驻站和跳站的组合控制是研究的热点.黄溅华等[4]令早到车辆驻站，晚点的车辆跳站，减少了公交车实际行驶状况与计划时刻表的差值，保证线路的行车间隔和各车辆的均匀载客.Cortés等[5]和Sáez等[6]建立了混合预测控制模式，结果表明该策略能分别减少乘客总出行时间的20%和10%.Milla等[7]考虑了交通拥堵等不确定因素，证明了混合策略优于单一策略.Nesheli等[8]基于新西兰的实际线路证明驻站—跳站策略能够有效地减少换乘率和乘客的出行时间.

在跳站控制中，部分乘客可能被车辆跳过起点或终点而不得不搭乘多辆公交车或额外借用其他交通方式以到达目的地.考虑到这些负面影响，研究者们提出了限流控制.它是一种通过限制上车人数来缩短车辆在站点的停靠时间，进而加速公交运行的控制方法.限流策略的研究还处于初级阶段，主要侧重于限流和驻站的混合使用.卢春秀[9]基于数学优化方法求解了使乘客总等待时间最小的控制方案，并与驻站方案和无控制场景进行对比，得出组合控制比其他两种策略更有利于减少乘客等待时间.Delgado等[10-11]以最小化乘客出行时间为目标，求解了每辆车在各站点的驻站情况和限流人数，结果表明相比驻站控制和不实施控制，组合策略对系统性能的改善效果更好.然而在这些研究中，尚未讨论以不同指标为目标时控制方案的差异，以及以何种指标为目标时组合策略的性能表现最佳.

为了完善这部分研究，本文提出了基于车头时距阈值的驻站—限流的组合策略，分析控制参数的取值对各性能指标的影响，并对比以不同指标为目标时的控制场景及其系统性能表现，最终探讨最优的组合控制方案，从而为实际公交控制提供理论指导.

1 基于车头时距阈值的公交控制策略

本文研究的公交线路为单向的公交专用道，沿线设置Ns个车站.在研究时段内，公交车每隔H0min从始发站相继发出.表1列出了本文中涉及的变量和参数.

驻站(或限流)的控制机理是[12-13]：若2辆车之间的距离过小(或大)，后车将在站点多停滞一段时间(或禁止部分乘客上车)以尽可能与前车拉开距离(或追赶前车).基于阈值的控制策略的核心是确定车头时距阈值.在此定义驻站控制参数h∗和限流控制参数l∗，h∗H0(或l∗H0)为车辆之间可接受的最小(或最大)的车头时距，即早到(或迟到)阈值.首车不受任何车辆的阻挡所以不实施任何控制.假定乘客从前门上车、后门下车，那么车辆在站点的乘客服务时间取乘客上车和下车时间中较大的值.

1.1 限流控制

车辆m到达站点i时，如果该车与前车m-1的离站时间差值大于迟到阈值，如式(1)所示，该车辆将限制上车人数，其允许的最大登车人数如式(2)所示；否则，上车的乘客数量只受车辆容量的限制，如式(3)所示.

1.2 驻站控制

(1)驻站时间计算.

当车辆m准备离开站点i时，若当前时间与前车m-1的离开时间小于早到阈值，如式(4)所示，车辆将在站点上驻留一段时间再发车.此时，将采用Fu等[12]提出的驻站方案计算Dm,i，如式(5)所示.如不满足条件式(4)，车辆即刻离站，且Dm,i=Am,i+κ+τm,i.

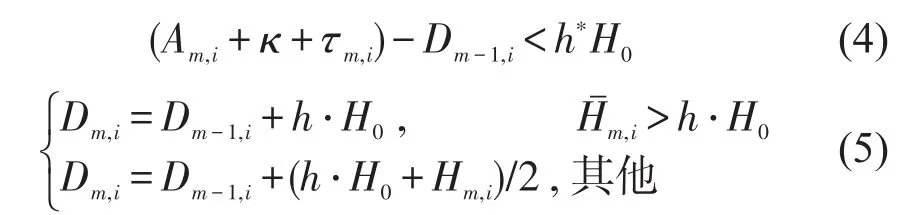
式中：Hˉm,i为前车车头时距(车辆m与前车m-1的时间间隔)和后车车头时距(车辆m与后车m+1的时间间隔)的平均值，即Hˉm,i=(D͂m+1,i-Dm-1,i)/2，D͂m+1,i为后车m+1离开站点i的估测时间，其值的计算将在后面介绍；h∗值的大小与驻站强度成正比，h∗=0表示不实施驻站控制，且h∗越大表明车辆在站点上平均停驻时间越长.

(2)车辆离开站点时间预测.

为了估测后车到达下游站点j的时间，模型记录了历史车辆在站点j-1和j之间的平均运行时间，从而计算该路段上的车辆平均运行速度v'j.后车m+1离开车站j的估测时间为

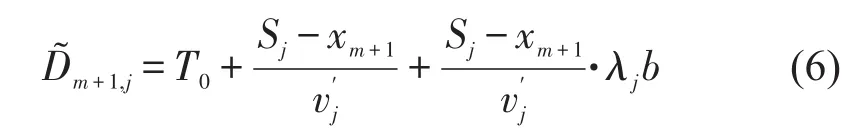
式中：T0为当前时刻；是车辆m+1从当前位置运行到站点j的时间.

2 基于元胞自动机的公交线路仿真模型

为了描述车辆的运行特征，本文基于元胞自动机经典的NaSch模型[14]进行车辆运动建模.元胞自动机是一种离散模型，主要表现在时间离散和空间离散两方面，即车辆在1个设定的最小时间步内可以向前行驶整数个格子(或元胞).其规则如下.

2.1 乘客运动

每一个时间步，乘客以固定概率λi60到达站点，其中θ=1表示t时刻有新乘客到达站点i，θ=0表示站点上无新乘客到达.

2.2 公交车站间移动

公交车按照NaSch模型的规则向前行驶：

(1)加 速.

车辆试图以最大速度在车道上行驶，且车辆最大加速度设为1，即

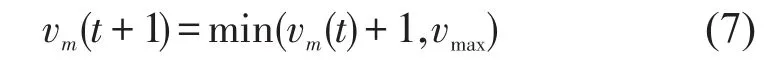
(2)减 速.

公交车将与前车保持安全间距，并在进站时减速，则

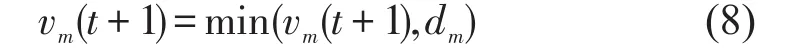
(3)随机慢化.

车辆在运动中受驾驶员行为或其他外部因素干扰会产生速度波动，为了简化这一现象，模型假设车辆在运动中会以概率pslow进行减速，即

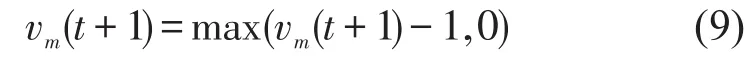
(4)位置更新.

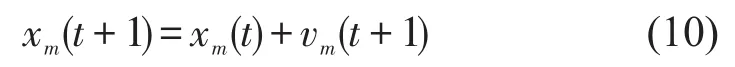
(5)判断是否到站.

2.3 公交车站点停靠

公交车在站点停靠过程分为2个阶段.

阶段1服务乘客状态，Am,i＜t≤Am,i+κ+τm,i.

公交车m刚到达站点i时，下车的乘客数为Offm,i=piψm,i，需要上车的人数为判断公交车m是否限流并计算允许的最大登车人数待乘客完成上下车后，设站点i上实际搭乘车辆m的人数是Onm,i，则乘客上下车耗时τm,i=max(b∙Onm,i,a∙Offm,i)；站点上和公交车上的乘客数量分别为：Wi(t)=Wi(t-1)-Onm,i，ψm,i=ψm,i+1+Onm,i-Offm,i.

若未实施限流控制，判断公交车是否需要驻站并确定车辆离站时间Dm,i.如需执行驻站策略，车辆进入阶段2；否则车辆即刻离站.

阶段2驻站状态，Am,i+κ+τm,i＜t≤Dm,i.此过程中，车辆不再允许乘客上车.

3 仿真模拟

3.1 仿真场景、参数设置及评价指标

本节将利用上述建模方法来模拟北京快速公交1号线的运行.该线路共设17个车站，各站点的相关属性如表2所示.模型参数设定如下：1个时间步为1s；单位元胞长3m，因此kdis=1 000/3=333.3；发车间隔H0=3min；公交车容量C=180；公交车长len=18 m=6元胞；车辆最大速度vmax=54 km/h=5元胞/时间步；车辆慢化概率pslow=0.2；开关门时间κ=10 s；单位乘客上、下车时间：b=2.0 s、a=1.5 s.模型通过5个指标来评估系统的性能，其定义如表3所示.为了描述乘客对等待时间的敏感度比在车时间要高的现实情况，模型设定等待时间价值是在车时间价值的2倍.此外，为防止过多的乘客被限制上车，l∗最小值取1.1.

表2 北京快速公交1号线站点信息Table 2 Stop information of BRT Line 1 in Beijing

表3 系统性能指标及其定义Table 3 System performance indicators and corresponding definitions

3.2 结果分析

(1)控制参数对系统性能的影响.

图1显示在不同h∗和l∗组合下的各个指标的数值分布特征.图1(a)显示随着h∗值的增加或l∗值的减小，车头时距的方差越小.说明严格的公交控制更有利于减少车辆的串车现象，保证车辆的稳定行驶.

一般情况下，公交系统的服务可靠性越高，车辆到达站点间隔越均匀，乘客在站点的等待时间越短.如图1(b)所示，当l∗保持不变时，随着h∗值的增加乘客候车时间越短.但是在限流控制下，提高服务的可靠性意味着更多的乘客被限制上车.这很可能导致因提高服务可靠性而减少的等待时间难以弥补部分乘客因限制上车而额外增加的等待时间，从而使所有乘客候车时间增加.也就是说，服务可靠性高的公交系统中的乘客不一定候车时间短.如图1(b)，当l∗≤ 1.4时，乘客的等待时间随着l∗的增加而减少.

乘客平均在车时间(或公交车平均运行时间)由站间移动时间和站点停靠时间组成.站间移动时间与服务可靠性有关，即串车现象越少，车辆之间的相互干扰越少，车辆在道路上自由行使的概率越大，车辆在站间的运行时间越短.站点停靠时间主要取决于上下车乘客的数量与驻站时间：驻站控制的增强会引起车辆在站点驻留的时间的增长.限流策略则能通过有效地限制上车乘客数量减少站点的停靠时间.综上，限流控制越强，乘客的平均在车时间(或公交车的平均运行时间)越小，这与图1(b)和图1(e)的结果一致.当限流较多时(l∗＜1.7)，只需辅助实施较弱的驻站控制(h*=0.4)便可缓解剩余的串车现象；而l∗≥1.7时，驻站控制减少串车进而提高站间速度的作用比在站点延缓车辆运动的作用大，此时乘客平均在车时间(或公交车平均运行时间)与h∗值成反比.

单位乘客的总出行时间由等待时间和在车时间共同决定.由图1(d)可以看出，在h∗不变的情况下，随着l∗的增加，单位乘客出行时间先减少后增加；较强的驻站控制对应较短的乘客出行时间.整体而言，乘客在h*=0.9且l∗=1.3时平均出行时间最短.

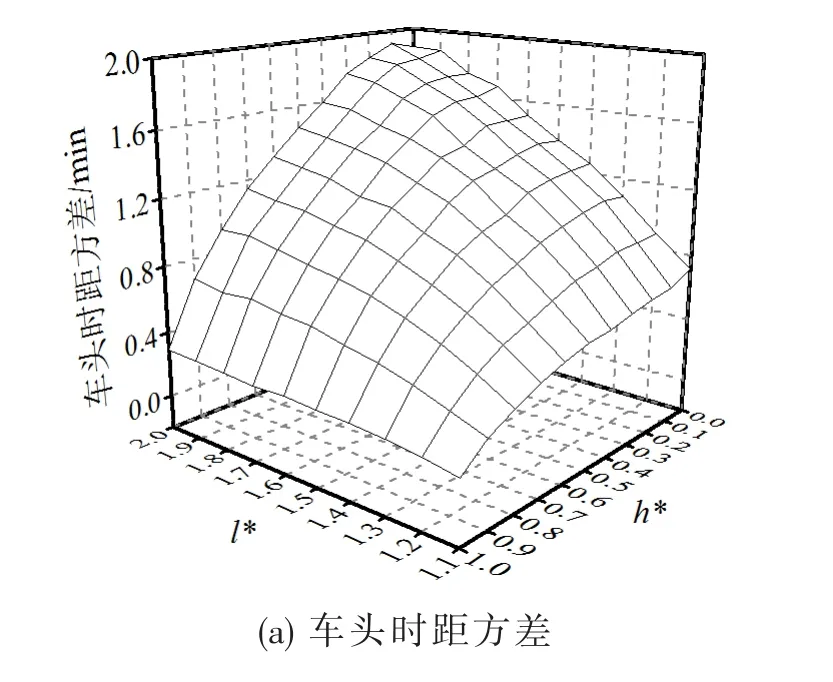
图1 不同h∗和l∗取值下系统性能表现Fig.1 The system performances with different value ofh∗andl∗

(2)策略对比.

表4列出了以最小化乘客平均等待时间和最小化单位乘客出行时间两种优化目标下各策略的控制参数取值，其中驻站和限流的数据是根据额外的仿真实验得出的.数据表明，不同目标的选取对驻站方案的设置没有影响，但是限流和组合策略的控制参数取值随目标的变化而改变.

表4 不同目标下3种控制策略的h∗和l∗的取值Table 4 Values forh∗andl∗ for three control strategies under different goals

图2列出了不同目标条件下，驻站、限流和组合策略相比无控制场景的系统性能改善情况.在下文分析中，某一特定策略是指某指标最小时该策略所对应的控制方案，如最小化乘客平均等待时间时的组合策略对应h∗=1.0且l∗=1.5的控制模式.图2(a)表明，最小化乘客平均等待时间时，组合策略在减小乘客在车时间或公交运行时间方面略弱于限流策略.虽然组合策略和限流策略的l∗取值相同，但是前者需在部分站点上停滞从而慢化了车辆的行驶.以最小化乘客总出行时间为目标时，组合策略在各个系统性能方面均优于或等效于驻站控制和限流控制，如图2(b)所示.

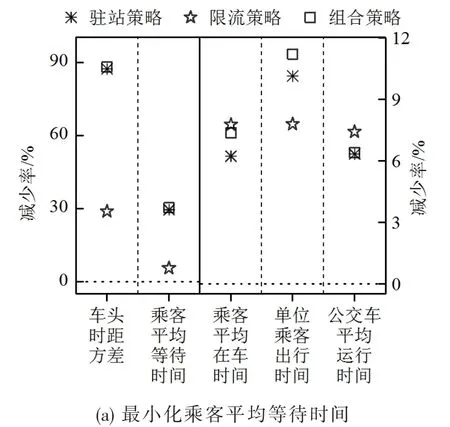
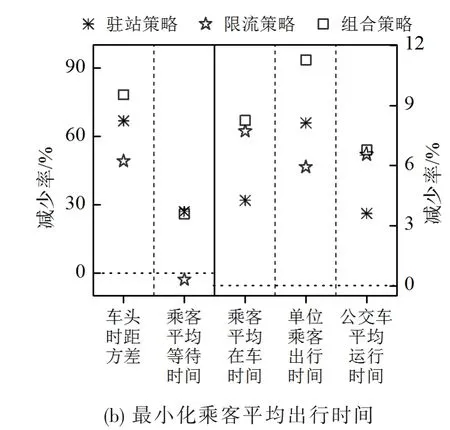
图2 3种策略比较于无控制场景的各指标的减少率Fig.2 The decrease percentage of each indictor with three control strategies compared to no-control scenario

图3对比了两种目标下的组合策略的实施效果，结果表明，以最小化乘客平均等待时间为目标时，组合策略能够获得更高的服务可靠性和更低的乘客平均等待时间，但是在提高乘客服务水平和降低公交运行成本方面，以最小化乘客平均出行时间时求解的组合策略是一种更好的选择.

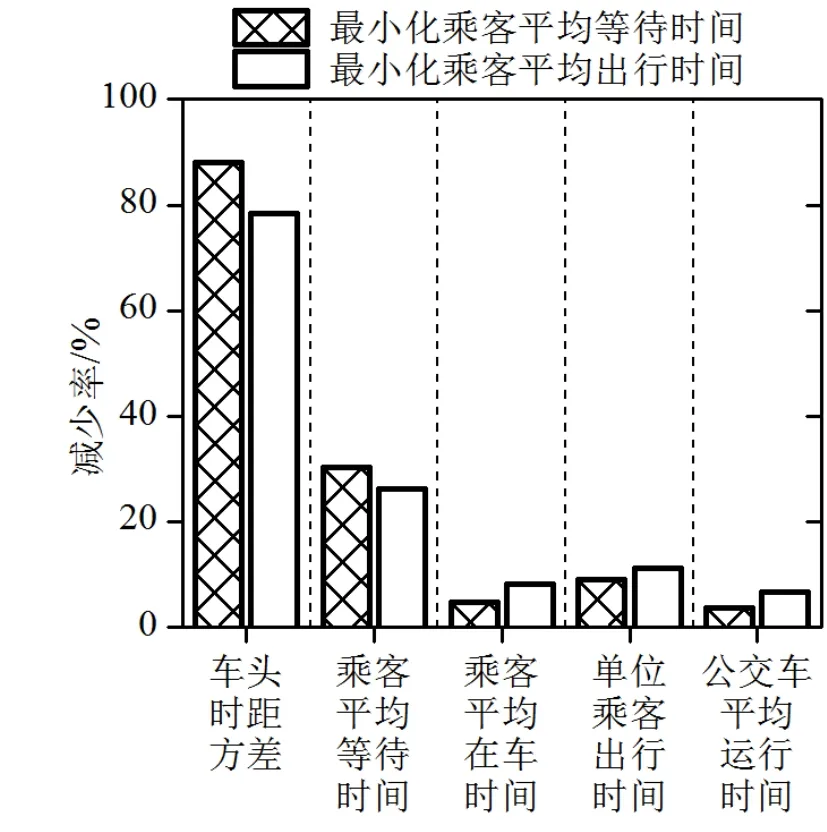
图3 两种目标下的组合策略性能对比Fig.3 The system performance of integrated control strategies with two different goals

4 结论

本文基于微观交通线路运营模型，对基于车头时距阈值的驻站—限流的组合控制策略进行了评估，结果表明：在追求不同系统性能目标时，组合策略的控制参数的取值具有差异；以最小化乘客平均出行时间为目标的组合策略，不仅在改善系统整体性能方面优于单一控制策略(驻站或限流)，且在提高服务水平和降低公交运行成本方面较最小化乘客平均等待时间为目标时所求组合策略的效果要好.注意到，本研究忽略了小汽车和自行车等其他车辆对公交车的运行影响，而这种车辆混合情况在中国非常普遍，该场景下的策略性能有待于进一步的研究.