深海管柱式气液分离器液相分离效率测量与分析
2018-09-11许承炜陈建义贾中会张西兆
许承炜, 陈建义, 董 腾, 贾中会, 张西兆
(中国石油大学(北京) 重质油国家重点试验室, 北京102249)
0 引 言
随着海洋油气资源开采范围向深水和极深水延伸,水下生产系统中传统的重力分离器体积庞大、设备笨重、投资高的缺点越发明显[1-2]。日益增长的需求刺激石油行业寻找一种新式紧凑型气液分离器,管柱式气液分离器(Gas-Liquid Cylindrical Cyclones,GLCC)应运而生。DAVIES[3]的研究表明:GLCC相比于传统重力分离器体积更加紧凑,分离效果更好。
GLCC由竖直上升管、倾斜管、筒体组成。气、液两相首先由竖直上升管流入倾斜管,倾斜管与筒体相切,且在连接处设计有渐缩筒体入口,以实现加速和造旋。在离心力和重力作用下,液相被甩到筒体边壁,最后从位于下部的液相出口管排出;气相则从位于上部中心的气相出口管排出,由此实现气、液两相的分离。分离过程中还可能出现部分液体被气体携带出气相出口管,即液相带出(Liquid Carry Over,LCO)现象,以及部分气体被液体携带出液相出口管,即气相带出(Gas Carry Under,GCU)现象。相关研究[4-6]表明:GCU发生时只带出了少量气泡,对分离性能影响较小;LCO的发生对分离性能造成了极大影响,使得液相分离效率成为衡量GLCC分离性能的主要指标。
目前,对LCO的研究大多集中在将GLCC应用于预分离场合或调节流量计和泵上游气液流量比[7]中,且主要关注LCO起始点,即确定安全操作区域。如ARPANDI等[8]在搅混流情况下提出的理论模型及CHIRINOS等[9]的修正模型均用于安全操作区域的确定。但此时GLCC气相出口和液相出口连通,不能适用于需要完全分离的场合。当GLCC应用于深海油气分离等需要完全分离的场合时,对液滴携带起始点之后效率变化规律的研究就成为工业应用中亟待解决的问题。复杂的多相流流体力学特性和操作条件的变化,使GLCC分离机理复杂,极大地阻碍了其在完全分离场合的应用[10],同时也导致缺乏LCO起始点之后液相分离效率的相关研究。本文采用试验研究的方法,对GLCC液相分离效率变化规律进行探索,初步建立GLCC液滴携带率分区模型,并得到相关的携带率与效率关联式,为工业应用提供参考。
1 试验装置与流程
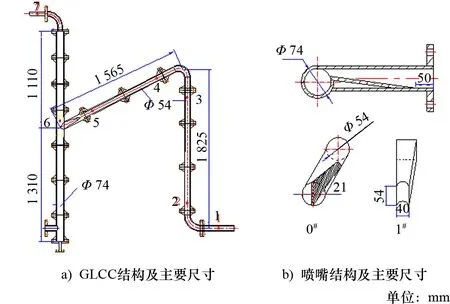
图1 GLCC主要尺寸及筒体入口结构
1.1 GLCC结构设计
GLCC采用有机玻璃进行加工,主要尺寸如图1 a)所示。筒体内径D为74 mm,高度为2 420 mm;入口倾斜管根据KOUBA等[11]的相关研究,向下倾斜27°,长度为1 565 mm,内径为54 mm;垂直上升管长度为1 825 mm,内径为54 mm。GLCC竖直上升管段、入口段以及筒体设置了编号为1~7的7个测压孔,用于安装压力传感器。试验分别采用0#新月型筒体入口和1#矩形筒体入口,如图1 b)所示。
1.2 试验装置与流程
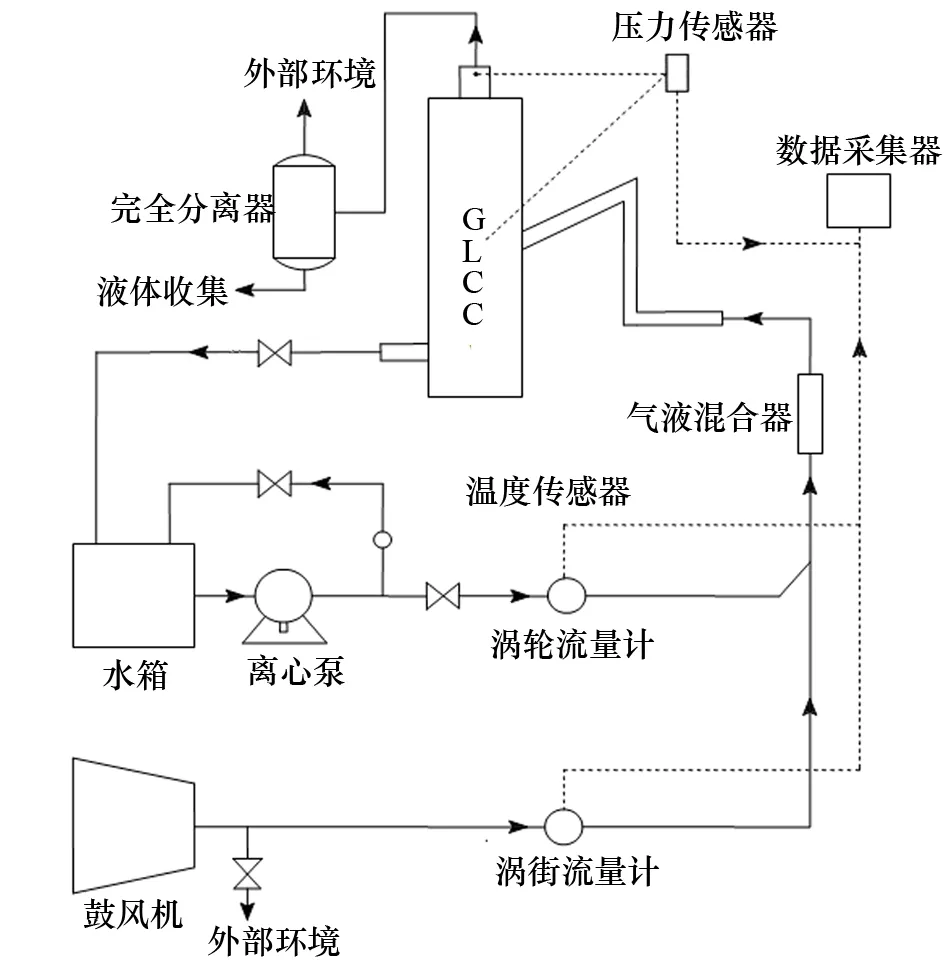
图2 GLCC试验装置流程图
试验装置与流程如图2所示。空气由高压风机鼓出,经涡街流量计(精度±0.1%)测量出体积流量Qg;水箱中的水由离心泵增压后流经涡轮流量计(精度±0.1%),测量出体积流量Ql。气液两相在气液混合器中进行混合,混合相经GLCC分离后,空气由筒体顶部气相出口管流出,进入立式丝网气液分离器,分离出挟带的液滴,利用烧杯收集测量带出液相的体积流量Qlo。水从GLCC底部流出,回到水箱循环利用,水箱液相支路还设置有温度测量表。气相、液相流量及GLCC平衡液位高度均可由相应的调节阀进行调节。由WANG[12]的研究可知:平衡液位在不是非常靠近倾斜管筒体入口的情况下,对LCO基本无影响。因此,每次调整气相、液相流量参数后,调节液位调节阀,使平衡液位稳定在距GLCC底部900 mm处5 min后进行测量。采用数据采集系统对气相、液相流量信号进行实时在线采集。
1.3 介质物性参数
试验以水与空气为介质。水的密度为995.7 kg/m3,动力黏度为0.8007 MPa·s,表面张力为71.18 m N/m;空气的密度为1.128 kg/m3,动力黏度为0.186 μPa·s。试验气相处理量为60~180 m3/h,液相处理量为0.9~3.6 m3/h。
2 试验结果与讨论
2.1 筒体流型

图3 上部筒体流型(1#)
研究[7,13-14]表明:GLCC分离性能在很大程度上受到倾斜管和上部筒体流型的影响。本文采用0#与1#筒体入口时流型变化基本相同,以1#入口结构为例,当气量相对较小时,与HREIZ等[7]观察的现象类似:倾斜管内流型主要为分层流,上部筒体空间含液量很小,液滴尚未被携带至气相出口,只在筒体入口上方有一圈连续的旋转液膜,如图3 a)所示。此时气液两相绝大部分在倾斜管内完成了预分离,且筒体内轴向气速相对较小,对旋转液膜的切削撕裂作用较弱,故此时气液两相被完全分离。当气量增大后,倾斜管内流型向环状流过渡,上侧筒壁出现一层较薄的液膜;上部筒体流型为搅混流,如图3 b)所示。此时倾斜管预分离作用开始减弱,大量液体被带入上部筒体空间。但由于旋流强度仍较弱,液滴不易被捕集到壁面,故此时筒体流型主要为搅混流,液相分离效率开始急剧下降。当气量继续增大后,旋流强度逐渐增加,对搅混液滴的捕集能力不断增强,此时液滴聚集在筒体壁面,出现缎带流与环状流特征,效率下降趋势逐渐平缓,如图3 c)所示。
2.2 液相分离效率
液相分离效率E定义为Qlo与Ql之比。不同Ql下对应效率随Qg的增大分为2个区域:完全分离区和效率下降区,如图4(采用0#筒体入口结构)所示。完全分离区对应上部筒体流型如图3a)所示,效率为100%,即安全操作区域。当进口气量超过临界值后,进入效率下降区。采用1#筒体入口结构时有相似结果。
GLCC效率问题本质上为耦合了环状流、湍流、旋流的三维复杂流场下竖直管液滴携带问题,同时在极大程度上受倾斜管筒体入口等结构的影响,相应的研究几乎空白。SAWANT等[15-16]提出用液相雷诺数与韦伯数表示的分区模型描述竖直管液滴携带率。本文借鉴该方法,将液相分离效率等价为气相出口液滴携带率问题。用F表示液滴携带率,即
F=1-E
(1)
MOLINA等[17]与HREIZ等[7]的研究结果表明:不同筒体入口形状与截面积对筒体入口附近液滴破碎和筒体入口上方的旋转液膜会产生影响,进而导致2种结构在相同气相、液相操作参数下进入上部筒体的液量存在差异。因此,引入筒体入口处液相雷诺数Rel描述液量与筒体入口截面积的综合影响。对于同一种结构,沿筒体轴向向上的气流是造成效率下降的决定性因素,直接影响到上部筒体内液滴的破碎和携带。引入筒体韦伯数We描述该影响:
(2)
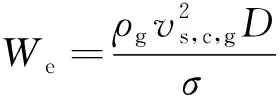
(3)
式中:d为筒体入口处水力当量直径;D参考SAWANT等[15-16]的研究,选取筒体直径;vs,i,l为筒体入口处液相折算速度(即Ql与筒体入口截面积之比);vs,c,g为筒体气相折算速度(即Qg与筒体截面积之比);ρg为气相密度;ρl为液相密度;μl为液相动力黏度;σ为表面张力。
金向红等[18]将液滴破碎理论应用于气液分离器,指出气液两相速度差使液滴表面产生压力差,进而导致液滴变形破碎加剧。此外,气相、液相流量的相对变化也影响了筒体入口上方旋转液膜的稳定性和上部筒体含液量的大小,进而对效率产生影响。研究发现:引入表示气相、液相流量及其相对变化关系的无量纲组合准数S有助于反映GLCC液相分离效率,即
(4)
0#筒体入口结构液滴携带率变化规律如图5所示,可以看出:液滴携带率,以单气相流量为横坐标时,不同液量间效率变化规律性较差,当S为横坐标时,相应的液滴携带率变化规律明显变好,这也说明了S的引入可以更好地表征效率的变化规律。气相、液相旋流对分离过程也产生了较大影响。但液相旋流主要体现在筒体入口下方,与重力共同作用使大部分液体进入到下部筒体空间;气相旋流则将上部筒体内液滴捕集至壁面,进而改变了上部筒体流型特征和液相带出机理。

图4 GLCC液相分离效率(0#筒体入口结构) 图5 GLCC液滴携带率
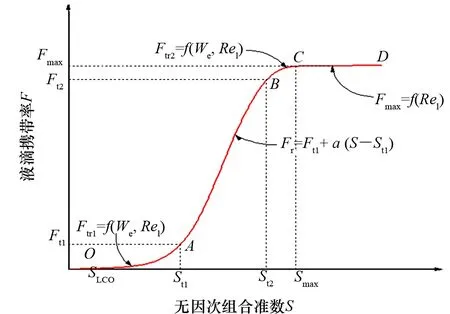
图6 GLCC液滴携带率曲线模型
3 液滴携带率与效率分析
3.1 液滴携带率模型

当液相雷诺数固定时,无量纲准数S退化为修正韦伯数,模型退化为各自液相雷诺数下对应的模型。当液相雷诺数不固定时,OA段表征对于达到液滴携带起始点的任一组操作参数,改变气相、液相流量使准数S增大,携带率随之增大。AB段不同液相雷诺数对应的液滴带出率呈线性上升趋势。BCD段,液滴带出率逐渐平缓,且在CD段达到最大稳定值。需要指出的是,这里所述的不同区域对应准数S所涉及的气液量都在各自分段范围内。
3.2 液滴携带率分区
3.2.1 携带初始区OA
OA对应液滴带出初始区。携带起始点O对应准数SLCO为液相雷诺数的函数,见式(5)。这是由于O点对应的韦伯数刚好可以满足液滴带出的条件,筒体上部空间表观持液率很小,带出主要受旋转液膜的制约,而旋转液膜厚度受到液相雷诺数的直接影响[7]。当S逐渐增大时,上部筒体表观持液率缓慢增加,使得OA段携带率Ftr1同时受到液相雷诺数与韦伯数的影响。
SLCO=e-1.239-1.612×10-4Rel
(5)
3.2.2 线性带出区AB
AB段携带率Fr与准数S呈现较强的线性关系,对应数据点基本集中到一条直线上,携带率曲线如图7所示。在气相旋流的影响下,部分液滴被捕集到壁面,但由于旋流强度相对较小使得二次携带严重,上部筒体流型仍为搅混流,带出机理为轴向气流对搅混液滴的直接携带。A点对应准数St1为液相雷诺数的函数,由此可得A点后液滴携带率为
Fr=Ft1+a(S-St1)
(6)
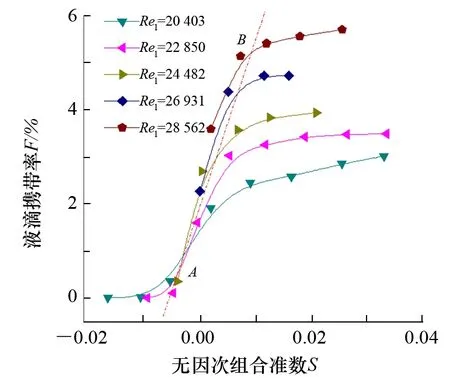
图7 GLCC拐点后液滴携带率
3.2.3 旋流过渡区BC、稳定带出区CD
携带率曲线在B点后上升趋势变缓,出现第二段过渡区BC并达到最大稳定值Fmax。BC段携带率Ftr2受韦伯数与液相雷诺数同时影响,且起点St2与终点Smax也为液相雷诺数的函数。稳定最大值Fmax只为液相雷诺数的函数,即
Fmax=f(Rel)
(7)
这是由于气速的继续增加不能将所有液体全部带出,SAWANT等[15]对环状流下竖直管的液滴携带试验也证明了这一点。GLCC相比竖直管还受到旋流作用的影响,气速越高,旋流作用越强,液体越不易被直接带出,这与轴向速度增加越易带出液滴相矛盾。BC段即为这一对矛盾的集中体现,随着旋流作用不断增强,搅混液滴被收集到筒壁,上部筒体流型出现缎带流与环状流特征,此时的带出机理主要为轴向气流对液膜的切削和上部筒体内壁处的液相短路[7],携带率曲线上升逐渐变缓。
3.3 液滴携带率与效率关联式
3.3.1 0#筒体入口结构携带率关联式
SAWANT等[15-16]、ISHII等[19]与SARKHI等[20]依据携带率曲线具有渐近于最大稳定值的变化趋势,提出采用双曲正切函数或者指数函数的形式描述液滴携带率。由3.1节的模型可知,GLCC液滴携带率具有类似规律,且变化趋势更加符合双曲正切函数,故尝试采用双曲正切函数建立0#筒体入口结构液滴携带率的关联式:
(8)
其中SLCO由式(5)确定。根据本文试验数据得到Fmax和Smax均为液相雷诺数的函数,即
(9)
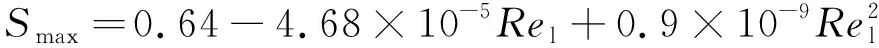
(10)
由式(5)、式(8)~式(10)得到的液滴携带率理论值与试验值,部分数据对比如图8所示,可以看出:由该方法确定的液滴携带率曲线和试验值吻合较好。液滴携带率对应的效率最大误差在1%以内,精度较高,在一定程度上揭示了携带与失效机理。
3.3.2 1#筒体入口结构验证
GLCC分离性能在很大程度上受到结构尺寸的影响,其中倾斜管筒体入口结构与尺寸就是一个主要的影响因素[1,7,21]。采用1#筒体入口结构对该方法进行验证,得到液滴携带率对应的效率理论值与试验值的误差如图9所示,可以看出:相应的效率最大误差在1.5%以内。通过验证可知:由双曲正切函数关联液滴携带率确定液相分离效率的方法精确度较高,基本满足GLCC工业设计与应用需求。
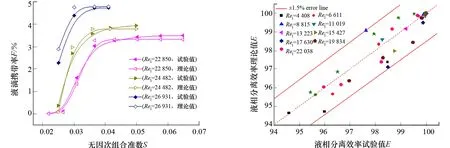
图8 液滴携带率试验理论值对比(0#) 图9 GLCC效率误差(1#)
4 结 论
(1) 引入表示气液量相对变化的准数S,证明该准数能较好地表述GLCC中液相效率的变化规律。
(2) 建立了GLCC液滴携带率曲线的分区模型,即可划分为携带初始区、线性带出区、旋流过渡区和稳定带出区,得到了影响值之间的数量关系式。
(3) 采用双曲正切函数对0#筒体入口GLCC液滴携带率进行了关联,并且关联式精度较高,基本满足GLCC工业设计与应用需求。关联式对应的效率最大误差小于1%。
(4) 利用1#筒体入口试验数据对该方法进行验证,得到相应效率误差在1.5%以内,认为该方法能够较好地应用于GLCC液相分离场合,基本满足工程设计需要。
