自升式平台圆柱式桩腿水动力载荷试验
2018-09-11吴子昂高一迪
李 英, 吴子昂, 程 阳, 李 晔, 高一迪
(1.天津大学 建筑工程学院 水利工程仿真与安全国家重点试验室, 天津 300072;2.中国船级社 海工技术中心, 天津 300457)
0 引 言
自升式钻井平台拥有作业稳定、造价低等优势,是目前国内外应用最广泛的钻井平台,其桩腿结构是自升式平台设计和建造的核心部件[1]。作用在桩腿上的波浪荷载对自升式平台的整体性能和作业能力有着明显的影响,桩腿强度的评估依赖于准确的波浪载荷计算[2]。自升式平台的桩腿是典型的海洋工程小尺度结构。目前,小尺度圆柱式结构所承受的波浪载荷计算主要基于莫里森公式,理论已经相对成熟,其计算主要依赖于拖曳力系数和惯性力系数[3]。这2个水动力系数的取值一般通过试验确定,对于形状规则的圆柱体和长方体的水动力系数已经有了广泛的研究[4-6]。王冬姣等[7]通过特征函数推导得到适用于深海浮式直立圆柱体的水动力系数。姚晓杰等[8]通过开展模型试验研究波浪要素对水平固定圆柱杆件水动力系数的影响。
自升式平台的桩腿由于齿条的存在,并不能简单应用圆柱体的水动力系数来计算流载荷和波浪载荷。对于桁架式桩腿,业内普遍根据美国船舶轮机协会规范通过拖曳力系数、惯性力系数、桁架桩腿的直径和面积进行波、流载荷计算[9]。然而,计算作用在自升式平台圆柱桩腿上的水动力时,通常需要对模型进行简化处理,造成水动力计算结果不够准确,影响齿条结构强度的评估精度。目前,针对自升式平台圆柱式桩腿水动力精确计算暂未形成业内通用的方法。因此,通过自升式平台圆柱式桩腿的模型试验测量其承受的波流载荷,并由此推算其水动力系数具有很重要的理论价值和工程实际意义。
本文开展圆柱式桩腿在流载荷作用下的水池模型试验,分析齿条对拖曳力的影响,并计算相应的拖曳力系数,研究来流角对拖曳力系数的影响;开展圆柱式桩腿在波浪载荷作用下的水池模型试验,分析齿条对惯性力的影响,并计算相应的惯性力系数,研究浪向角对惯性力系数的影响;分析试验数据研究自升式平台带齿条圆柱式桩腿的水动力特性,为自升式平台圆柱式桩腿的设计提供参考。
1 小尺度结构水动力理论
1.1 莫里森(Morison)方程
目前,与波长相比尺度较小细长柱体(对于圆柱体D/L<0.2)的波浪力计算,在工程设计中仍广泛采用Morison方程,它是以绕流理论为基础的半理论半经验公式。作用于直立圆柱体任意高度z处单位柱高上的水平波浪力可表示为
(1)
因此,作用在一定长度圆柱体上的总波浪力Fh可将式(1)从高度z1~高度z2进行积分:
(2)
1.2 拖曳力系数和惯性力系数
影响圆柱体系数的主要因素有:雷诺数、KC数、柱面的相对粗糙度以及波浪相位角。对于给定的试验模型,相位角一定时,水动力系数的控制因素是雷诺数和KC数,KC数与波高成正比。作用在一定长度柱体上的最大拖曳力和最大惯性力分别在不同的相位角,因此可采用线性波理论分别推导圆柱体的CD和CM。
拖曳力系数可表示为
(3)
式中:Fd为试验测得的流力;ρ为水密度;D为圆柱式桩腿直径;U为试验实际流速;L0为圆柱式桩腿的入水深度。
惯性力系数可表示为
(4)
式中:Fh为试验测得的波浪力的波峰值;γ为水容重;H为波高;K为计算系数,可表示为
(5)
式中:k为波数;d为水深;η为波幅。
2 试验过程
2.1 试验模型

图1 1∶6.4比尺制作的2种桩腿模型
以某自升式平台圆柱桩腿为原型,设计制作1∶6.4几何缩尺比的试验模型。此外,为对比研究齿条对圆柱式桩腿波流载荷的影响,制作同等直径的光滑圆柱模型作为对比试验模型。水池试验模型的设计原则上应满足几何相似、流体相似和动力相似。由于雷诺数相似和重力相似不能同时满足,针对海洋工程结构的模型试验的特性,试验选取重力相似准则。模型采用硬质灰塑管(Polyvinyl Chloride,PVC)材料,制作完成的模型如图1所示,模型几何尺寸见表1。采用自制的测力传感器测量作用在桩腿上的水平剪力,即流力和波浪力。
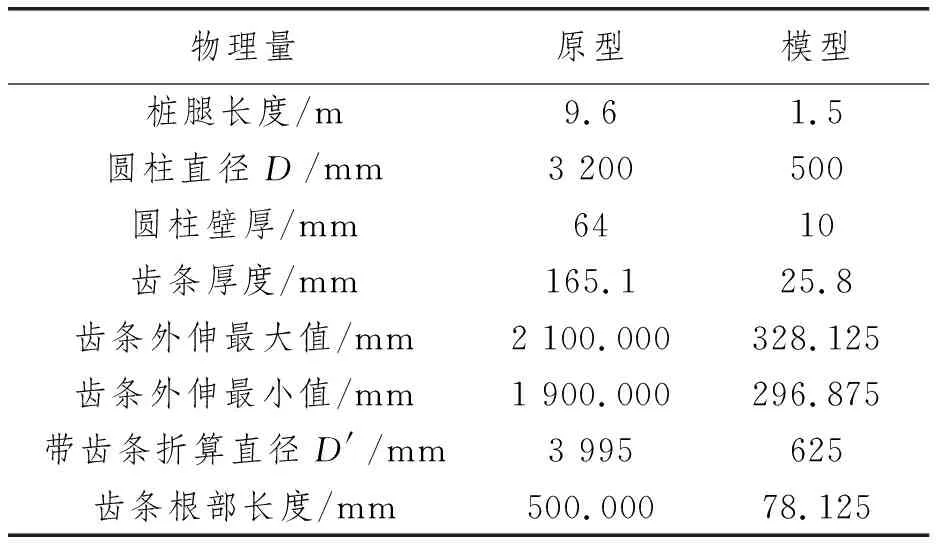
表1 桩腿模型参数
2.2 试验设备和装置
天津大学船舶工程试验室拖曳水池主尺度为137 m×7 m×3 m,如图2所示。水池一侧安装了造波装置,可以产生规则波,最大波高可达25 cm。水池另一侧安装消波装置,消波性能良好。另外,水池两侧轨道上装有拖车装置,可以拖动试验模型用以模拟作用在桩腿上的流载荷。其他用于模型试验研究的主要测试仪器和设备包括:(1)浪高仪,用于测量实际波高。(2)测力杆、测力传感器,用于测量模型在水池中受到的水平剪力。(3)振动信号数据采集系统,用于实时采集、记录试验过程中的动态数据。(4)数码照相机、摄像机,用于拍摄各个试验工况及其过程。
测力传感器下端通过法兰与圆柱式桩腿模型刚性固定,上端通过自制的法兰与拖车刚性固定。为便于记录,试验中规定齿条所在平面与波流0°入射方向平行,安装在水池中的试验模型如图3所示。

图2 天津大学拖曳水池 图3 桩腿试验模型
2.3 试验工况
2.3.1 流载荷试验
保持水池内水体静止,拖车匀速拖动模型,通过相对运动模拟均匀流,用测力传感器测量圆柱式桩腿受到的总水平流载荷。通过调整拖车的移动速度模拟不同的试验流速;通过水平转动桩腿模型模拟不同的来流角度。测试工况见表2。
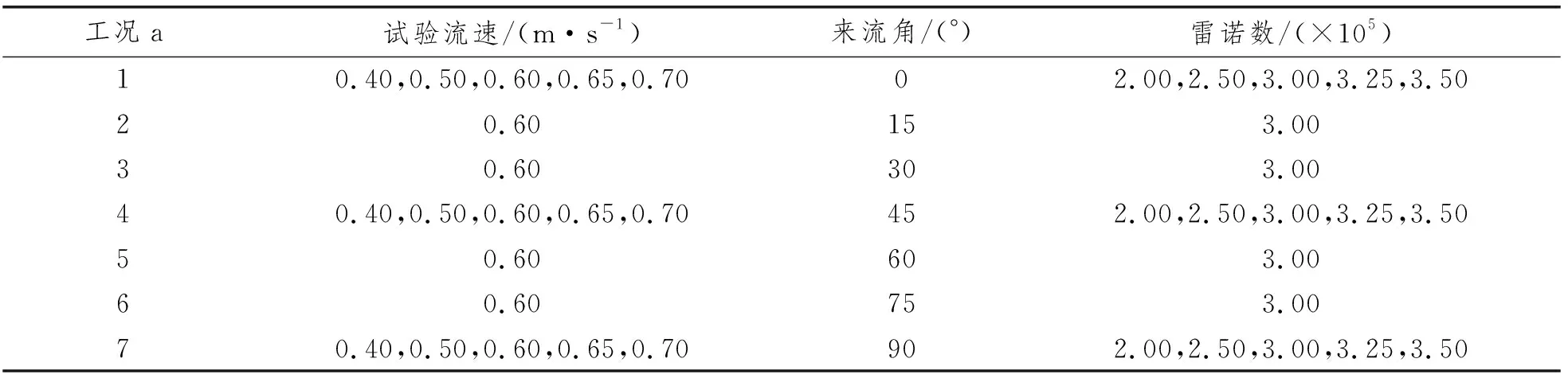
表2 流载荷试验工况
2.3.2 波浪载荷试验
为了消除波浪反射对试验的影响以生成良好的规则波,试验时将拖车开至水池80 m处,距离造波机57 m。将模型固定在静水中,用水池一端的造波机制造规则波。改变波周期与波高,分别测量在不同工况下圆柱式桩腿受到的波浪载荷,通过转动模型测量不同浪向角下桩腿模型受到的水平波浪力。波浪载荷试验测试工况见表3。
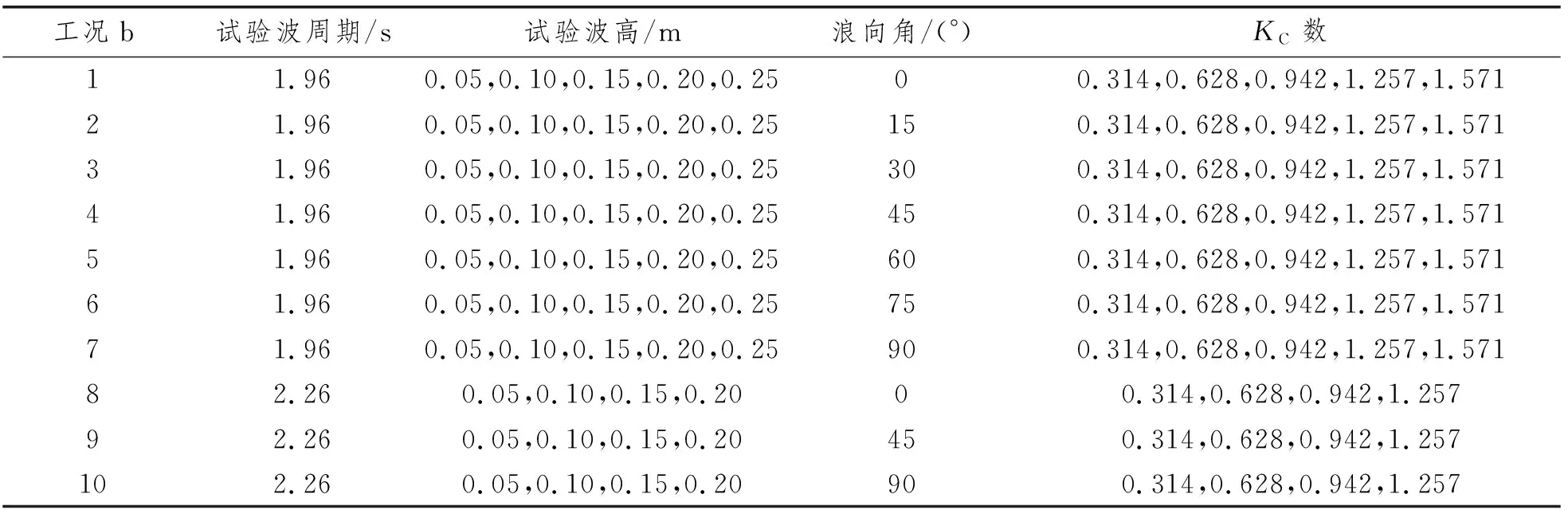
表3 波浪载荷试验工况
3 水平流载荷
试验中测试系统的采样频率设为100 Hz,分析稳定后测量作用在模型上的水平流力。图4为来流角0°、45°和90°时,不同流速作用下,光滑圆柱腿和带齿条的圆柱桩腿上的拖曳力,可以看出:雷诺数在2.0×105~3.5×105这一范围内,随着流速的增大,作用在圆柱式桩腿模型的水平流力呈增大趋势。齿条对圆柱式桩腿模型的水平流力有明显的增大作用。在增大桩腿的受力面积的同时,齿条也改变了流场,进而改变了水流与桩腿的相互作用。当来流角为90°时,有齿条桩腿承受的流力约为无齿条桩腿承受的流力的3倍。
图5为来流角为0°、45°和90°时,圆柱腿和带齿条圆柱腿的拖曳力系数,可以看出:雷诺数在2.0×105~3.5×105这一范围内,拖曳力数受速度影响不大。来流角对拖曳力的影响较大:随着来流角的增大,拖曳力系数也不断增大。当来流入射角为0°时,拖曳力系数在0.5~0.6这一范围内变化;当来流入射角为45°时,拖曳力系数在0.70~0.85这一范围内变化;当来流入射角为90°时,拖曳力系数在1.35~1.60这一范围内变化。
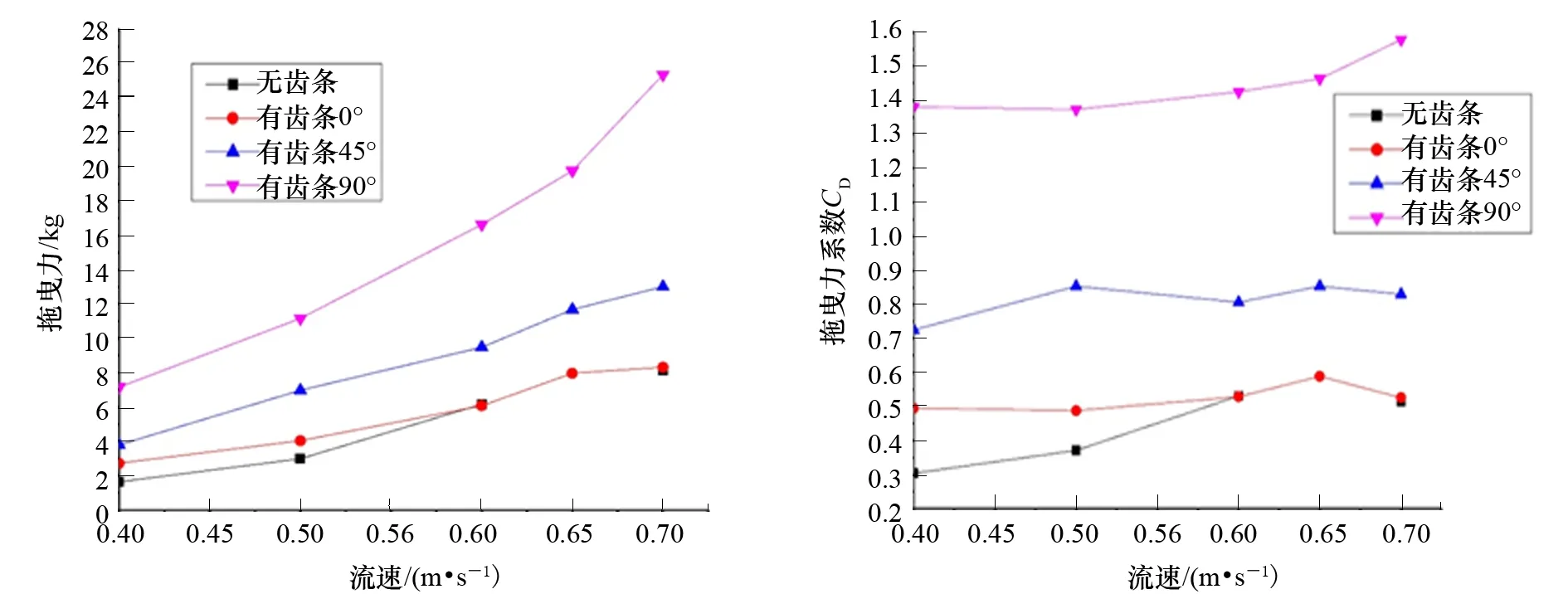
图4 不同流速、来流角时的流力 图5 不同流速、来流角时的拖曳力系数CD
图6为流速0.6 m/s时,不同来流角下带齿条的圆柱腿上拖曳力系数随来流角的变化,可以看出:当来流角小于30°时,齿条对拖曳力系数的影响很小;入射角在30°~75°时,拖曳力系数随着来流角的增大呈线性增大趋势;当来流角大于75°时,拖曳力系数维持在1.4左后,受来流角影响减缓。
4 水平波浪载荷
通过数据采集系统,得到不同工况下圆柱式桩腿模型承受的水平波浪载荷的时程曲线。图7为浪向角0°,波周期1.96 s,波高为0.25 m时,桩腿受到的水平波浪力。
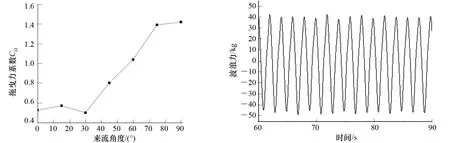
图6 CD随来流角的变化 图7 波浪载荷时程曲线
分别提取不同工况下无齿条圆柱桩腿上的最大作用力,并与圆柱桩腿(无齿条)惯性力系数为2.0时的理论数值比较,结果见表4,可以看出:波周期为1.96 s和2.26 s,波高为0.05 m时,波浪力的试验误差比较大,均大于10%,其他结果均证明了试验方法的准确性。

表4 圆柱型桩腿(无齿条)水平波浪力
图8为波周期为1.96 s和2.26 s时,带齿条桩腿上所作用的最大波浪载荷随波高的变化,可以看出:作用在桩腿上的波浪载荷随波高的增大呈线性增加。当波高不变时,波周期越大,桩腿承受的波浪力越小。波高相同,但波周期由1.96 s增大至2.26 s时,桩腿承受的波浪力减小量约为13%~18%。另外,当浪向角小于30°时,齿条对桩腿承受的波浪载荷影响不大;之后随着浪向角的增大,桩腿承受的波浪载荷快速增加;当浪向角为90°时,相同工况下带齿条桩腿承受的波浪力约为不带桩腿承受波浪力的1.2倍。
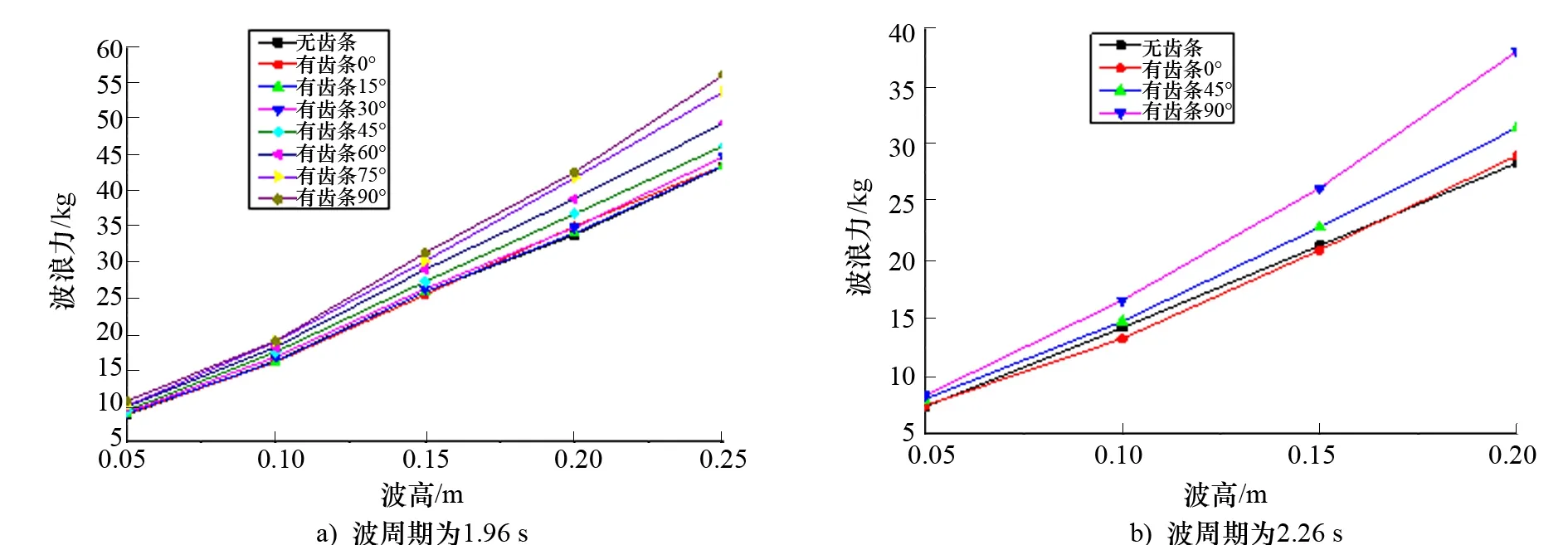
图8 不同波周期、不同波高条件下桩腿的波浪力
由理论与试验数值的对比分析可知:波高为0.05 m时的试验误差较大,因此分析惯性力系数时不考虑波高为0.05 m工况的试验数据。由于试验波高的范围较小,KC数在0.628~1.571范围内,均小于2,对惯性力系数影响不是很大。图9为波周期为1.96 s、2.26 s时,带齿条桩腿上作用的惯性力系数随浪向角的变化,可以看出:当浪向角小于30°时,惯性力系数随浪向角增长缓慢;当浪向角大于30°时,由于齿条的影响,惯性力系数随浪向角的增大不断增大。
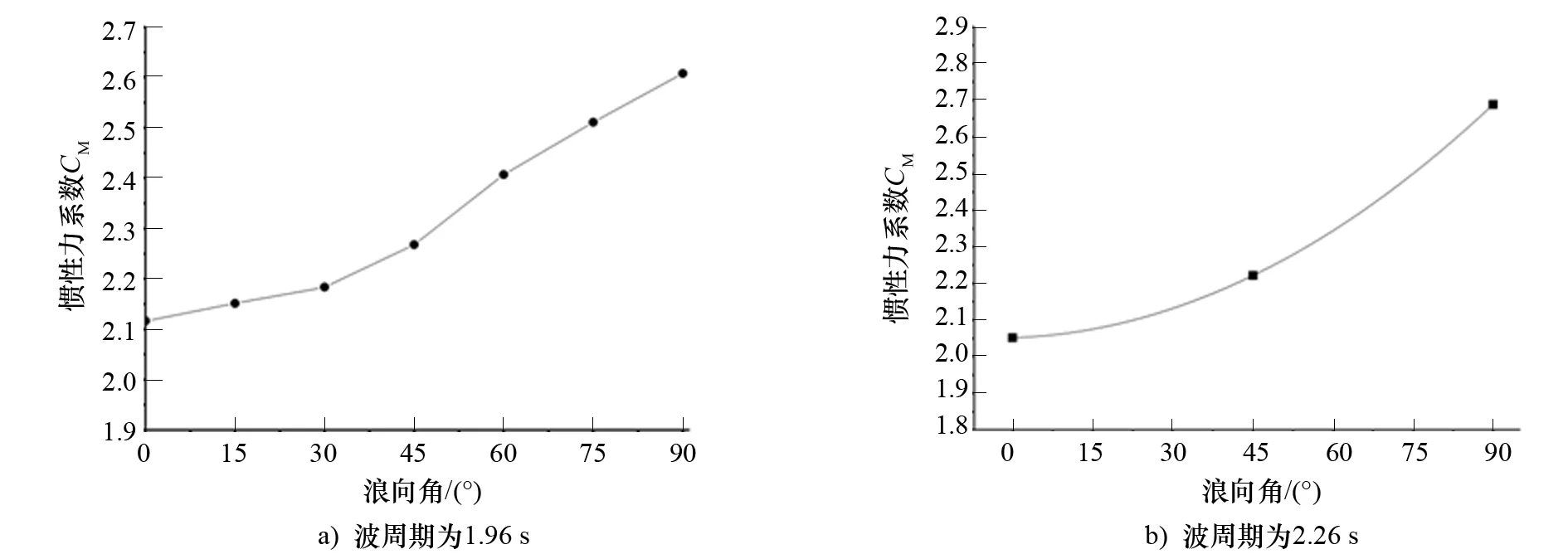
图9 不同波周期、不同浪向角下的惯性力系数
5 结 论
(1) 自升式平台圆柱桩腿承受的拖曳力以及惯性力分别随流速以及波高的增大而增加。
(2) 拖曳力系数CD受雷诺数影响较小,但来流角对齿条拖曳力系数有一定影响。当来流角小于30°时,齿条对拖曳力系数的影响较小;来流角在30°~75°之间时,拖曳力系数随着来流角的增大呈线性增大趋势;当来流角大于75°时,拖曳力系数又趋于稳定。
(3) 齿条对惯性力系数CM的影响效果与CD相似:当浪向角小于30°时,CM受浪向角影响较小,导致齿条对桩腿惯性力系数的影响同样较小。当浪向角大于30°时,齿条对CM的影响才开始显现,即惯性力系数随浪向角的增大而不断变大。
