基于粒子群算法的轨道车辆设备布局优化

黄辉嘉，杨 岳，魏晓斌，陈 晓

(1. 中南大学 交通运输工程学院，长沙 410075；2. 株洲电力机车有限公司 大功率交流传动电力机车系统集成国家重点实验室，株洲 412000）

轨道车辆车上设备的布局直接影响车辆整体的重心位置，不合理的布局可能会带来较大的轴重差，以及整车左右两边的不平衡。目前，一般采用人工方法对车上设备进行布局，虽然在一定程度上可满足技术要求，但是反复进行布局调整费时，且轨道车辆的运行还存在不安全因素。因此，采用合理有效的算法进行轨道车辆设备的自动布局，对于整个轨道车辆的设计与安全运行具有重要作用。

目前，轨道车辆设备布局的优化大多针对轨道车辆车下悬挂设备进行优化[1]，对设备布局的约束条件没有全面考虑，对轨道车辆车上设备的布局优化研究不足，或者算法冗杂不易实现，从而影响了预测精度。针对这一弊端，以及轨道车辆车上设备需要分别在不同车厢内进行布置的约束条件，本文建立分区域的轨道车辆设备布局的重心优化模型，利用改进惯性权重因子的粒子群（PSO）算法，实现轨道车辆车上设备总重心布局与轨道车辆中心位置最小化优化。最后通过算例证明本文提出的轨道车辆设备布局优化模型及算法的有效性。

1 优化数学模型

1.1 车辆初始布局模型

轨道车辆设备布局设计的主要目标是规划设备的物理排列位置和顺序，以其达到最佳平衡状态，方便对轨道车辆设备进行设备布局优化求解。

为了计算出整个轨道车辆的重心位置，首先需要在轨道车辆上建立参考坐标系，整个坐标系统采用笛卡尔坐标系。坐标系的原点设在整个轨道车辆自身中心位置，x轴正方向设定为轨道车辆的司机室方向，x轴正方向的左侧设定为y轴的正方向。便可以将轨道车辆中各设备的位置用坐标形式表示。

令n为待优化布局的设备数量；待优化布局设备分在m个不同区域中；(xi, yi)为设备i的重心位置；(x, y)为轨道车辆总重心坐标， mi为第i个设备的质量，如图1所示。

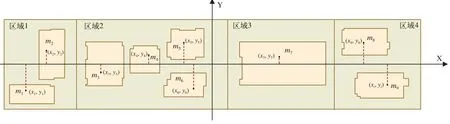
图1 某轨道车辆设备初始布局简图

已知n个待优化布局设备的总重心坐标为：

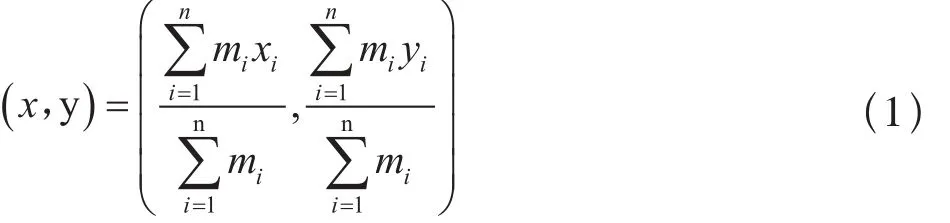
轨道车辆车体重心的计算：轨道车辆上的设备分为固定设备（位置确定的设备）以及非固定设备（需要进行布局的设备），固定设备及车体本身对于各轴转矩，即为固有转矩，而需要布置的设备对于各轴转矩，则随着其位置的改变会发生变化。

令C和E分别表示车内固有设备相对于x和y轴的转矩；按照轨道车辆优化后的设备总重心与轨道车辆中心的距离最小化原则，可以建立如下设备布局优化模型：

1.2 目标函数

考虑到实际情况，在轨道车辆设备布局过程中，对水平方向，即y轴方向的平衡布置要求更高，因此对于此多目标规划的问题，可以简化为单目标规划，即轨道车辆重心的x坐标的位置转化为一个约束条件，因此模型的目标函数转变为：

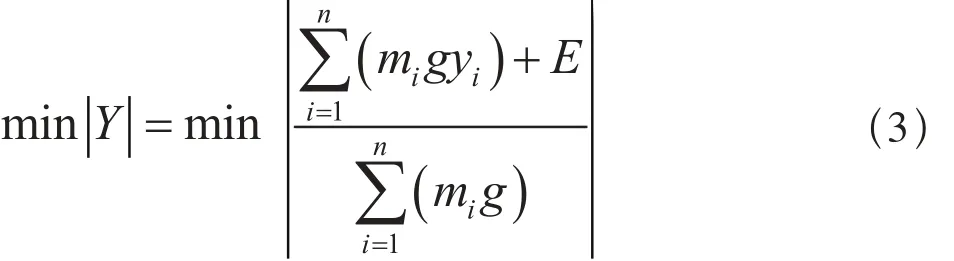
1.3 约束条件

对于上述的优化模型，必须满足一定的约束，才能用于实际的布局优化。

（1）设备外轮廓约束：轨道车辆车体在设计过程中，不同的设备会放置在不同的区域，各个设备的位置不能超过区域的边界，即设备边界顶点在 轴方向的最大、最小坐标需在区域边界内，则：

（2）设备几何干涉约束：将设备的干涉问题转化为多边形的干涉问题，考虑多边形干涉主要有两种情况，即相交和包含。解决思路为：列出所有设备干涉的集合，然后取补集即可。此处将优化后的两设备重心之间的横纵距离与两设备重心之间设备长度作为衡量因子。

（3）设备间距约束：设备之间需要间隔一定距离。假定设备之间的间距不能超过距离λ。具体实现方法为，将每个设备的边界放大（1/2）λ。

（4）轨道车辆总体重心在x方向位置的约束：根据轨道车辆质量分配计算要求，在这里允许轨道车辆重心在 轴方向的位置有20 mm的偏差，即：

2 轨道车辆设备布局优化数学模型求解

2.1 粒子群算法

对于轨道车辆设备布局问题，由于其变量较多，且约束条件也多而复杂，采用常规算法进行求解很难得到其最优解，而粒子群（PSO）算法具有很好的全局优化搜索能力和较快的收敛速度[2-3]，可以高效地解决这一问题。

设在一个D维的目标搜索空间中，有N个粒子组成一个群落，其中，第i个粒子表征为一个D 维的向量 ：Xi={xi1, xi2,…, xiD}T, i=1, 2,…, N，第 i个粒子的“飞行”速度也是一个D维的向量，记为：Vi={vi1, vi2,…, viD}T, i=1, 2,…, N，第i个粒子迄今为止搜索到的最优位置称为个体极值，记为：pi={pi1,pi2,…, piD}T, i=1, 2,…, N，整个粒子群迄今为止搜索到的最优位置为全局极值，记为：pg={pg1, pg2,…, pgD}T，为了更好地控制算法的探测和开发能力，改善粒子群算法的收敛性，在找到这两个最优值时，引入惯性权重ω，粒子根据式（6）和（7）来更新自己的速度和位置：

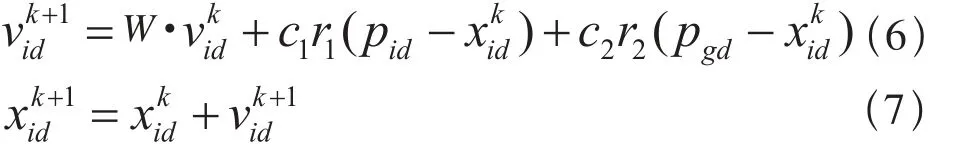
其中，c1和c2为学习因子，也称加速常数；r1和r2为[0,1]范围内的均匀随机数， i=1, 2,…, D；vij是粒子的速度，r1和r2是介于0和1之间的随机数，增加了粒子飞行的随机性。式（6）右边由3部分组成：第1部分代表粒子有维持自己先前速度的趋势；第2部分代表粒子有向自身历史最佳位置逼近的趋势；第3部分代表粒子有向群体或邻域历史最佳位置逼近的趋势。

惯性权重ω描述了粒子上一代速度对当代速度的影响，起到平衡算法全局搜索和局部搜索能力的作用。当ω值较大时，局部寻优能力弱，全局寻优能力强；反之，则局部寻优能力增强，而全局寻优能力减弱[4-6]。标准PSO算法在迭代前期收敛速度很快，但是到了后期收敛速度明显变慢，甚至停滞[7]。考虑到不同粒子间的个体的差异，因此采用线性权值递减策略，可以明显提高优化的效率[8]，即：

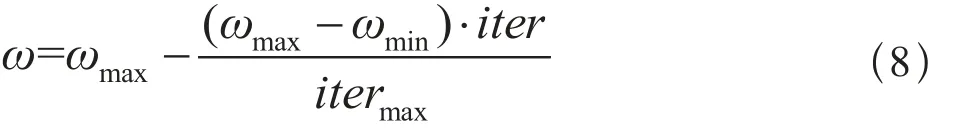
其中，ωmax和ωmin分别为ω的最大值和最小值，iter和itermax分别为当前迭代次数和最大迭代次数。

2.2 算法求解

为了使轨道车辆设备布局优化后的总重心坐标无限接近于轨道车辆中心坐标，即（0, 0），设计的适应度值函数如下：

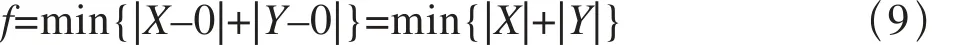
其中，（X, Y）为轨道车辆设备布局优化后的总重心坐标。具体的算法流程，如图2所示。

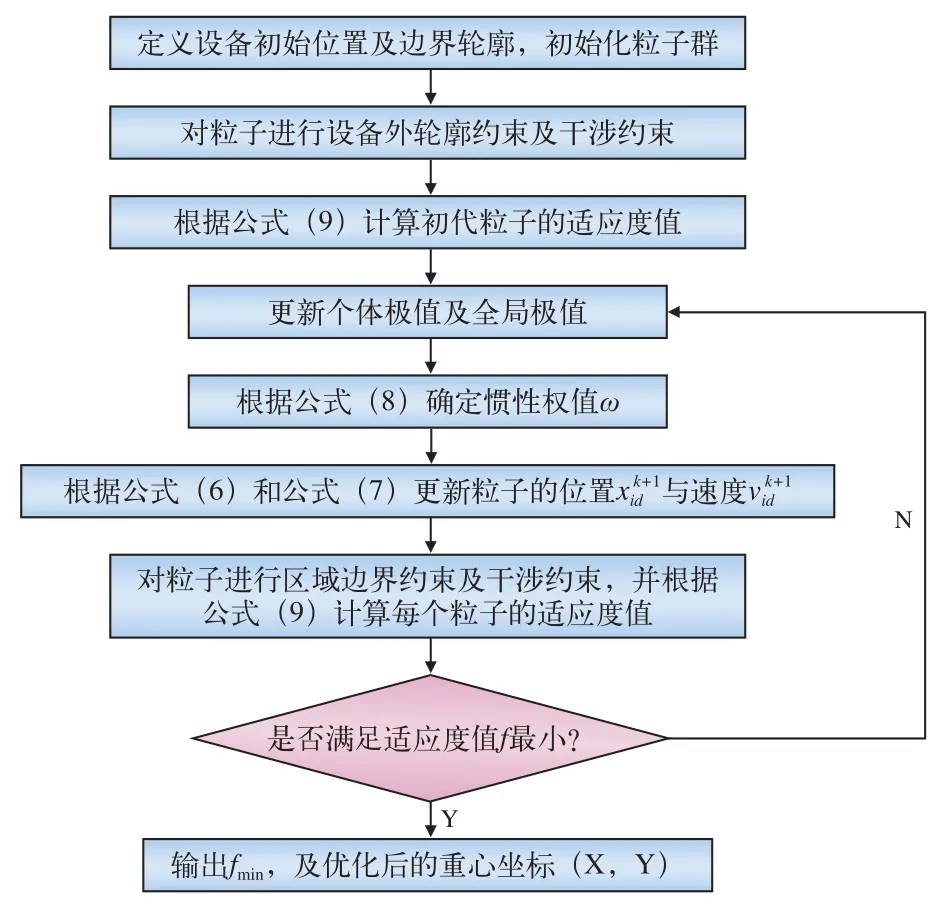
图 2 设备布局PSO算法流程图

3 算例

根据上述算法，采用Matlab选择某焊轨车车型进行验证。该轨道车辆外形图如图3所示，轨道车辆长度L=19 300 mm，宽度W=2 520 mm，各个设备总质量m=38 309 kg，重力加速度g=9.8 m/s2。

图3 某焊轨车外形图

在对整个轨道车辆的布局模型分析时，对于轨道车辆上的设备，用多边形来描述其轮廓，在进行计算之前，需要对各个设备的轮廓进行简化，以方便用其重心位置来表示其轮廓位置，如图4所示。

以某焊轨车车上某一组设备为例，其相关信息，如表1所示，为了提高计算的效率，通过排除车上一些固有位置的设备以及一些小重量设备，得到本次需要布局的设备，相关参数及属性模块，如表1所示。

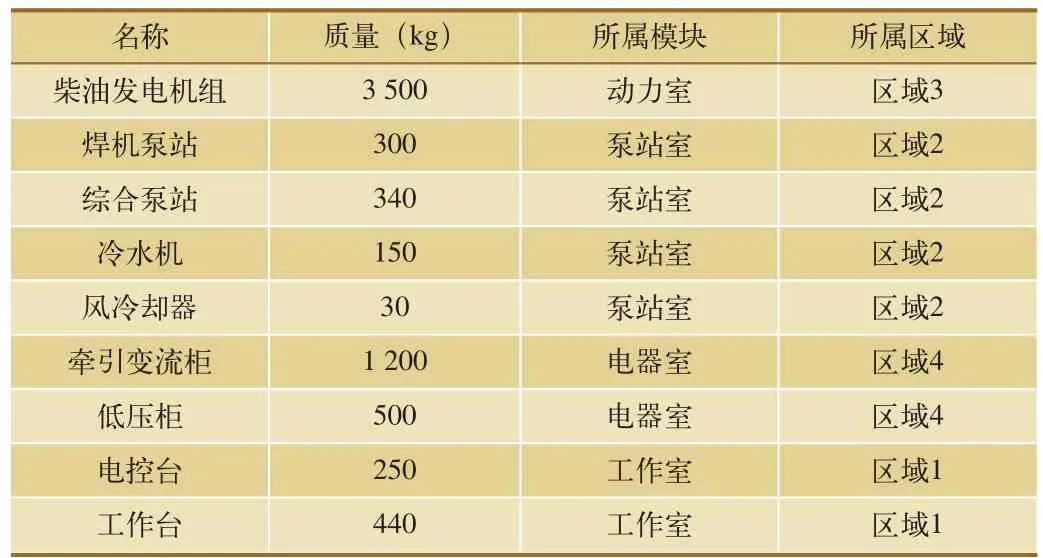
表1 车架上部布局设备参数

各个设备的初始位置坐标，如表2所示。

算法的参数值如下：群体粒子个数为50，最大迭代次数为30，学习因子c1=c2=2，惯性权重系数最大值和最小值分别为0.9和0.4。采用上述的粒子群算法求解该算例的布局优化问题，计算结果，如表3所示。

从图5的收敛曲线中可以看出，大约在第6次迭代处，算法达到收敛，此时最小适应度值为0.171 1。

优化后的设备总重心坐标（单位：mm）为（0.171 1，1.668 7×10-10）。由表2各项设备布局初始位置参数通过设备重心计算公式可算出设备初始位置的总重心坐标为（0.253 5，–0.007 4）。对于总重心位置的优化，PSO计算结果较初始位置优化了67%。

表2 各个设备布局初始位置参数

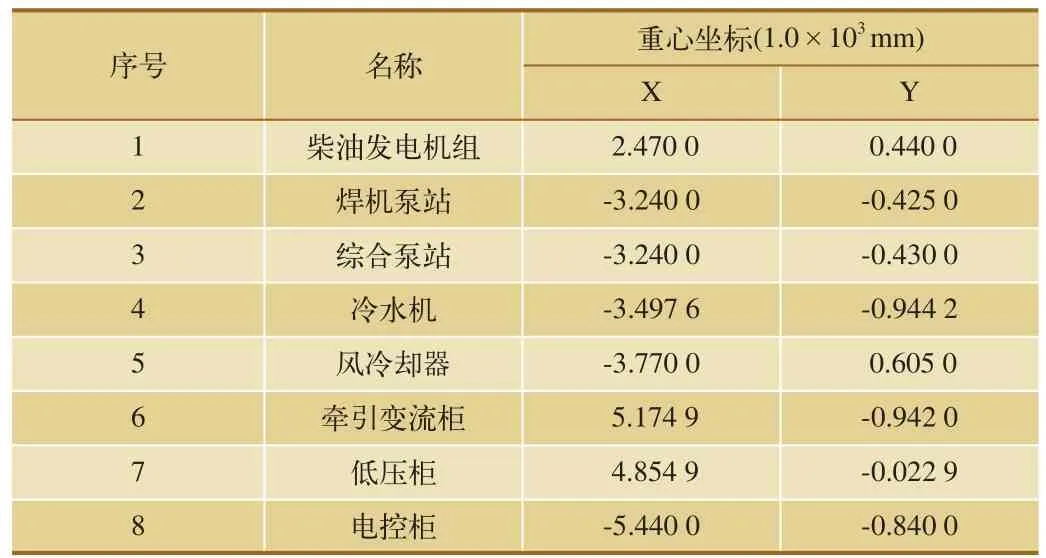
表3 粒子群算法设备布局优化结果

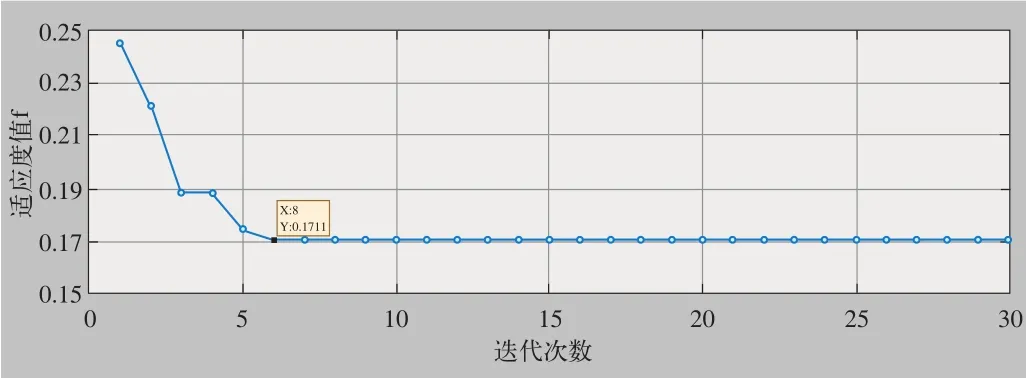
图5 适应度值与迭代次数关系图

4 结束语

针对轨道车辆设备布局设计的设备总重心无限接近于轨道车辆中心的原则，采用简化设备轮廓建立布局优化的数学模型，提出利用粒子群算法的基本思想来求解轨道车辆设备布局优化模型。结论如下：

（1）针对轨道车辆结构特点和设备优化布局的要求，建立了分区域的轨道车辆设备布局优化模型，该模型充分考虑了设备布局间的干涉问题，设备间距问题，区域化轨道车辆边界约束问题以及x与y轴方向上转矩最小化问题。

（2）引入PSO算法，对所建立的布局优化模型进行设备总重心优化求解，采用线性递减权值策略，引导算法向全局最优解方向收敛。

（3）焊轨车设备优化布局算例表明，该算法精度高，收敛速度快，稳定性好，设备优化设计效果显著。本文设计的算法有效实现了轨道车辆设备布局优化。