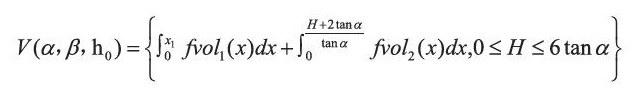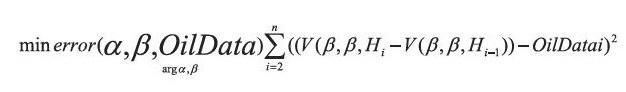罐容表变位标定中的最小二乘法应用

陈颖

摘要：储油罐在使用一段时间后会由于地基变形因素使罐体的位置发生不同程度的倾斜，导致罐容表发生变化，因此需要定期地对罐容表进行重新标定。储油罐变为分为横向移位与纵向倾斜，横向移位中分为高于、低于、处于三种状态，并将储油罐分为球冠体与圆柱体两部分进行纵向倾斜研究，建立储油罐的油量与高度之间的关系，利用最小二乘法确定对应值并验证模型的可靠性。

关键词：罐容表；变位；标定；最小二乘法

加油站有若干个储存燃油的地下储油罐，需要根据罐内油位的高度与储油量之间的关系标定罐容表，以此反映油位的高度与储油量之间的变化，但是由于外部因素的影响，导致储油罐的位置会发生偏移，从而罐容表也会发生相应的变化，需要重新对罐容表进行标定。为了能够更好地解决储油罐变位导致罐容表标定失真的问题，以储油罐作为研究对象，采用微元法思想建立储油罐变位标识的数学模型，并利用最小二乘法的原理确定变位的参数，对罐容表进行准确标定。

一、建立模型

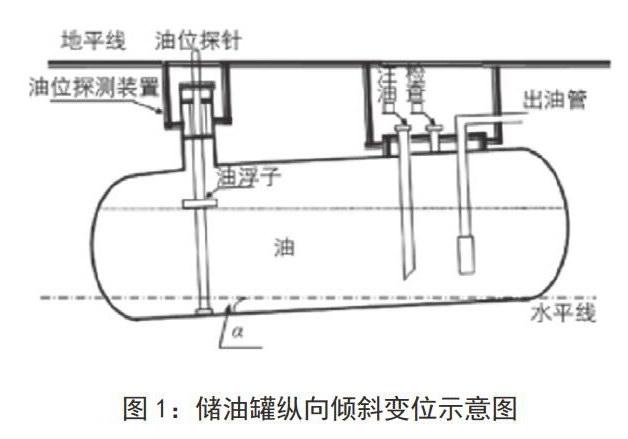
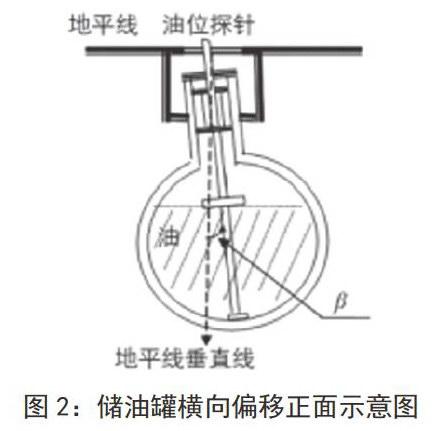
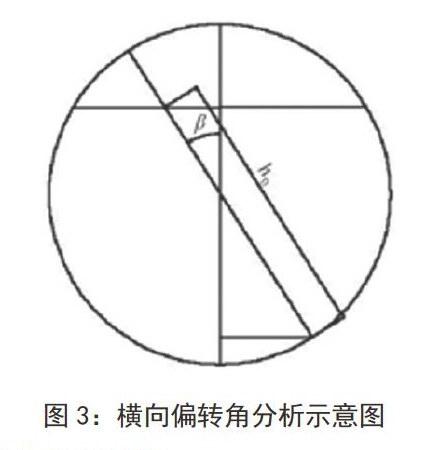
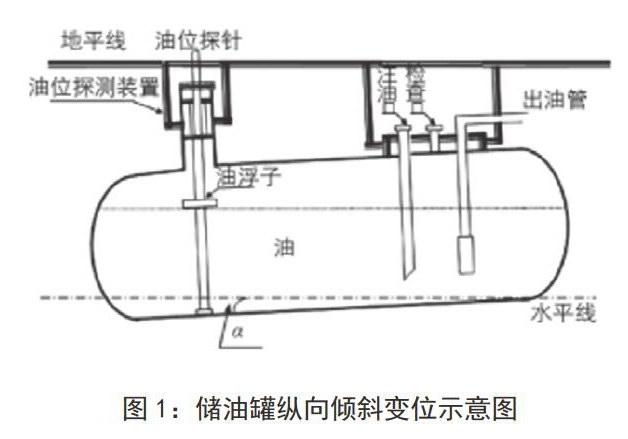
将储油罐作为研究的对象，在对储油罐进行建模的过程中需要考虑两个因素，储油罐纵向倾斜变位和横向偏转倾斜，如图l、图2所示，为了使问题变得简单容易理解，采用单一变量法，只考虑纵向倾斜，将罐内中的油位分成模块进行分析，得到每一种情况下罐内油体积与油位高度，将油体积、高度与变位参数建立关系式，然后再考虑横向偏移，确定与油高度的关系式，最后综合考虑横向偏移与纵向倾斜，建立整个储油罐变位的数学模型。

二、储油罐油位高度的计算方法

根据储油罐的油位高度，遵循接近实际情况的原则，通过仔细分析将罐内油位的高度进行分工。为了保证罐内油体积的均匀性，选取正常的油位高度情况进行计算，实际的储油罐是一种不规则的几何图形，两端为球冠体，中间部分是圆柱体。

根据微元法思想得到圆柱体的体积为：

利用劣弧弓形的面积公式，得到球冠体的体积为：

三、模型求解过程

根据罐内油量监测数据可以得到不同时刻的储油量，同时能够计算出对应油位高度的该变量，通过公式：

通过上述公式能够计算出实际储油量的该变量，并将该种问题归结为非线性最小二乘问题，利用最小二乘法原理，建立基于储油罐变位识别的非线性规划模型，公式为：

其中，OilData表示的是油量的数据；H.表示的是第i条数据对应的罐容表的读数。

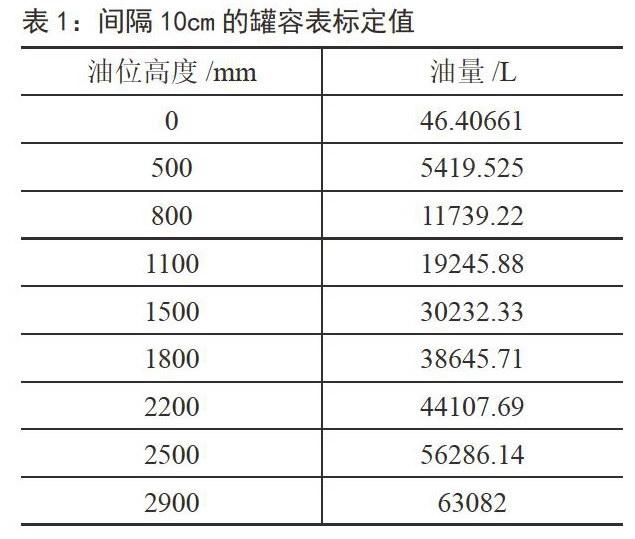
使用MATLAB软件进行编程，根据检测的进出油量以及油位高度，利用非线性规划的方法解决α和β的最优解法，计算出变位参数值，得到罐体变为后油位间隔的罐容表标定值，如表1所示。

四、模型分析

将实际的出油量与理论上的出油量进行线性拟合，如图4所示，横向坐标为实际测定得值，纵坐标是数学模型中的理论值，相应的系数为R-0.999，理论值与实测值基本相同，两者存在的误差较小，说明在进行模型设计时是较为合理的，能够哦实现罐容表的重新标定。

对油位的高度进行随机扰动，H’=H（1+0.001*rand（-1，1）），采用MATLAB软件进行计算，得出α和β的值，比较没有进行扰动时α和β的值，当α的变化幅度在0.1%时说明较为稳定，抗干扰能力较强，但是β的值会发生明显的变化，说明抗干扰能力较低。

五、结论分析

通过对储油罐变位标识所建立的数学模型得出的变位参数值与结果进行对比后，α的误差比β的误差小，针对现有的數学模型而言，该模型对油位高度的工况划分更接近真实的情况，计算出的变位参数值的误差也较小，对罐容表的标定更加准确，具有非常重要的使用价值。

六、结束语

当罐容表的位置发生纵向倾斜与横向移位时会对罐体造成一定程度的影响，不仅需要考虑到液体的静压力引起的罐壁形变，还要考虑到长期使用后造成的形变，当储油罐发生变位时纵向倾斜角度α与横向移位角度β的角度最小，因此要忽略储油量测量时的误差，因为误差本身来源于系统本身。通过设定问题的方式反应实际情况，然后再进行试验，研究罐容表标定模型，对罐容表进行重新修订，通过确定未知修订已知的方法进行研究具有很强的普遍性。