龙门式大跨度梁的结构设计与仿真
2018-09-10侯红玲孙允璞赵永强
侯红玲, 孙允璞, 王 飞, 赵永强
(1.陕西理工大学 机械工程学院, 陕西 汉中 723000; 2.陕西汉江机床有限公司, 陕西 汉中 723003)
现代测试扫描设备通常采用两种结构形式,即立柱式和龙门式。立柱式结构的优点是立柱有效行程大,而横梁的行程较短,适合于较小规格或矩形截面的工件测量;而龙门式结构的纵梁和横梁的有效行程相对较大,适合于较大规格或近似方形截面的工件测量[1-3]。
本文所涉及的测量设备的测试范围定为12 m×8 m×10 m,其中横梁长度为12 m,纵梁的实际长度为9.8 m,横梁和纵梁被架在10 m高的立柱顶端,横梁托板及其附件载荷为300 kg。最终确定为主体结构采用龙门式,如图1所示,一根横梁的两端支承在两根相互平行的纵梁上,横梁可以沿着纵梁上的导轨滑动,根据测量要求,各梁在实际运行中的直线度误差保证≤2 mm。因此在结构设计过程中分两步进行处理:一是尽可能在横梁工作变形的基础上保证横梁的加工精度;二是在加工后按照横梁的实际载荷对导轨进行调试,最终满足实际使用要求。

图1 测量设备的主体结构原理
1 大跨度梁的结构设计
图1中的中间横梁为大跨度梁,横梁的两端支承在滑块1和滑块2上,滑块1和滑块2分别由两个伺服电机单元驱动并在两根纵梁导轨上支承滑动,横梁上的滑块3用于安装另一移动轴,滑块3连同驱动电机单元及其附属装置的总重量设计为300 kg。两侧的两根纵梁各有三个支承位,与横梁相比纵梁的支承跨距较小。因此,两根纵梁和一根横梁将采用通用的结构尺寸,文中以横梁为研究对象。横梁的力学模型如图2所示,工作过程中,滑块3在横梁导轨上左右往复运动,即滑块3的支承位记为C和D,横梁左端A和右端B分别支承在滑块1和滑块2之上,用L表示横梁跨距,用x表示滑块3在横梁上的具体位置,用d表示滑块的支承距离。
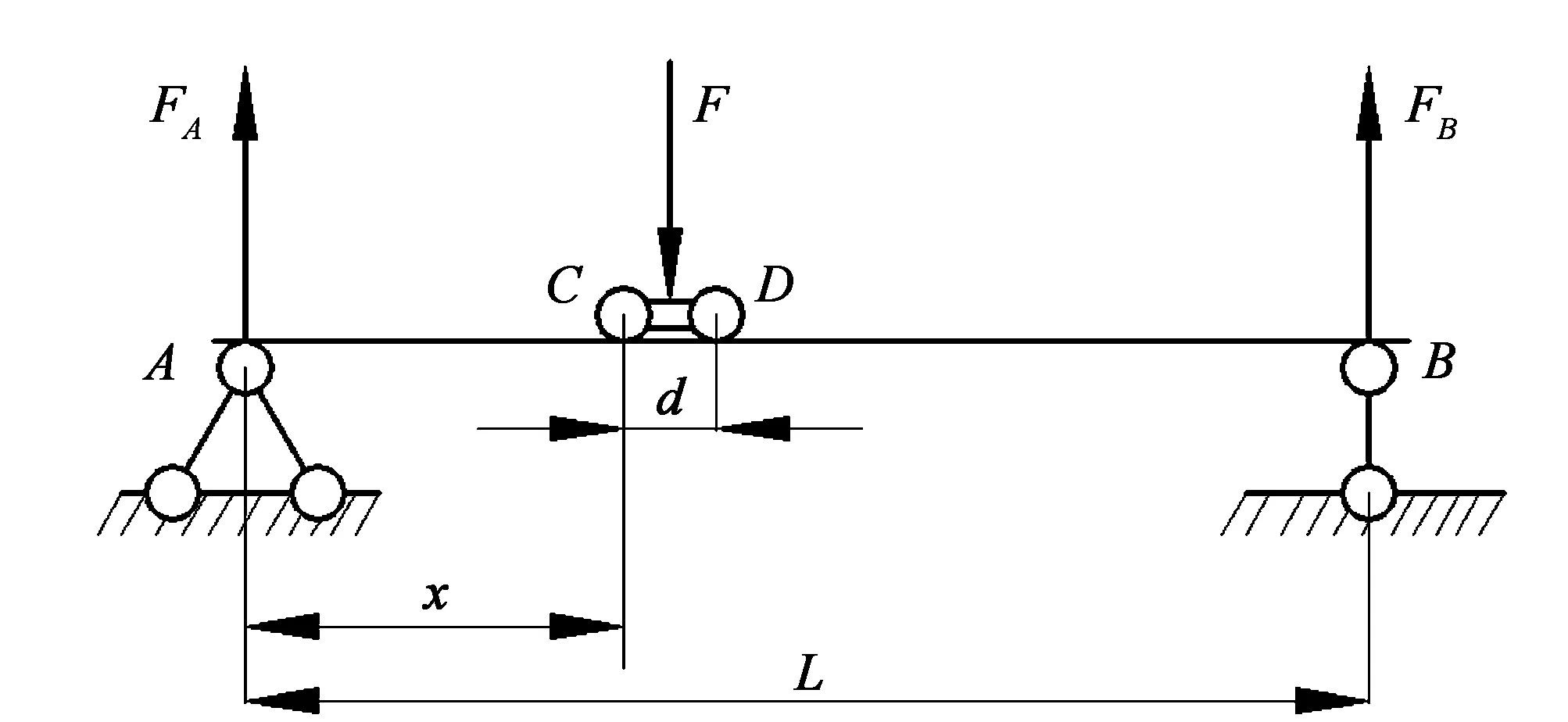
图2 横梁的计算简图
(1)横梁弯矩最大时滑块3的位置
如图2所示,电机通过滑块在导轨上移动,简支梁承受一个集中力F,所以分在滑块3的两个支承点C和D的力相等,即
(1)
由力矩平衡方程∑MB=0,可得
(2)
(3)

(4)
(2)横梁弯矩的极大值表示为
(5)
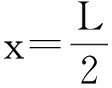
(3)横截面正应力计算
(6)
式中σ为正应力,M为横截面上的弯矩,Iz为横截面对中性轴z的惯性矩,y为所求应力点的纵坐标。
由以上公式可知,在横截面上离中性轴最远的各点处,正应力值最大。当中性轴z为截面的对称轴时,则横截面上的最大正应力为
(7)
令
(8)
则
(9)
式中,Wz为弯曲截面系数,其值与横截面的形状和尺寸有关。一般矩形和圆形截面的弯曲截面系数可以从相关书籍中查找,对于型钢截面的弯曲截面系数也可以从型钢规格表中查到。
由以上可知横梁的最大正应力发生在最大弯矩的横截面上距中性轴最远的各点处,而该处的切应力等于零。此外,纵截面上由横向力引起的挤压应力可忽略不计。因此,横截面上最大正应力所在各点处于单轴应力状态[4]。根据以上推导过程计算出矩形截面横梁的最大工作正应力σmax=59.47 MPa,未超出材料的许用弯曲正应力[σ],即满足如下判据
(10)
根据现有的型材截面以及加工工艺要求,可选的横梁截面形状如图3所示。
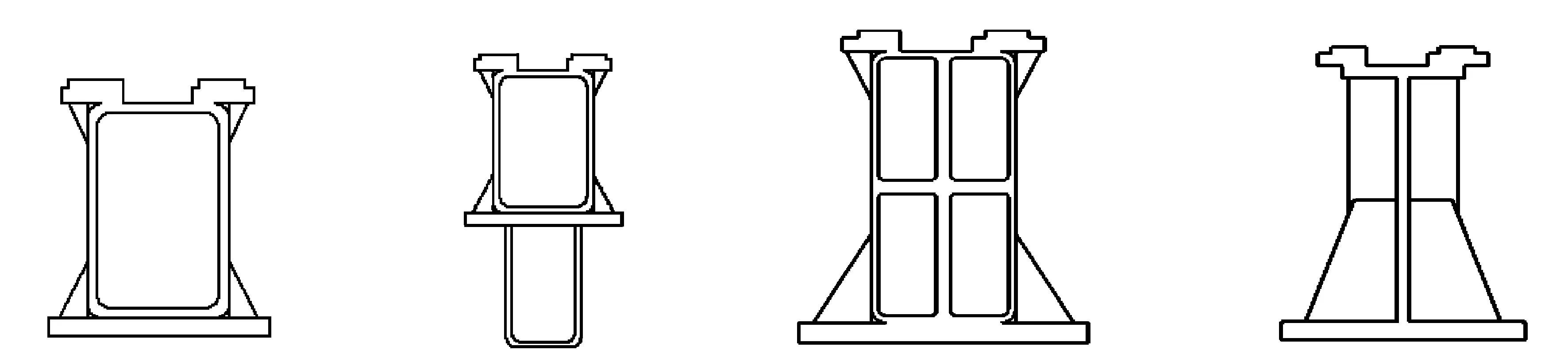
(a)矩形 (b)矩形下肋板 (c)四方管型 (d)H型侧肋板图3 横梁的4种不同截面形状
图3中所给出的4种不同的横梁截面形状,在上侧布置了导轨安装面,在不同位置分布了加强筋和肋板,使得不同截面的横梁弯曲截面系数Wz很难准确计算。因此,后续将采用有限元分析方法对不同截面形状的横梁进行强度和刚度校核。为了保证后期计算及仿真的一致性,横梁的上表面为导轨安装面,分布有加强筋和肋板,导轨安装面的结构尺寸相同,加强筋和肋板的布置方法一致,各板材的壁厚相同。
2 大跨度梁的有限元模型建立
2.1 大跨度梁的三维模型建立
建立准确、可靠的模型是有限元分析的前提之一。本文结合工程实践要求,需要在横梁上附加电机、托板、滑块等零部件,但这些零件对横梁的整体结构影响不大,可以忽略。为了方便后续仿真与对比,对不同截面的横梁结构进行如下简化[5]:
(1)将横梁上的非承载件去除,并等效为相应载荷;
(2)将结构中的焊接部分认为是理想焊接,焊接材料与副车架材料相同;
(3)在横梁中点处设计一个长宽高分别为340 mm、280 mm、30 mm的板块,等效替换托板,以便载荷的施加。
具体的仿真实现步骤如下:
首先在三维建模软件UG8.5中建立如图3所示的4种不同截面的横梁简化模型。然后将模型保存为通用的*.igs格式,并导入ANSYS Workbench15.0中,导入后的横梁模型如图4所示[6]。最后对导入的模型进行静力学仿真分析,完成对横梁的强度、刚度计算与校核。
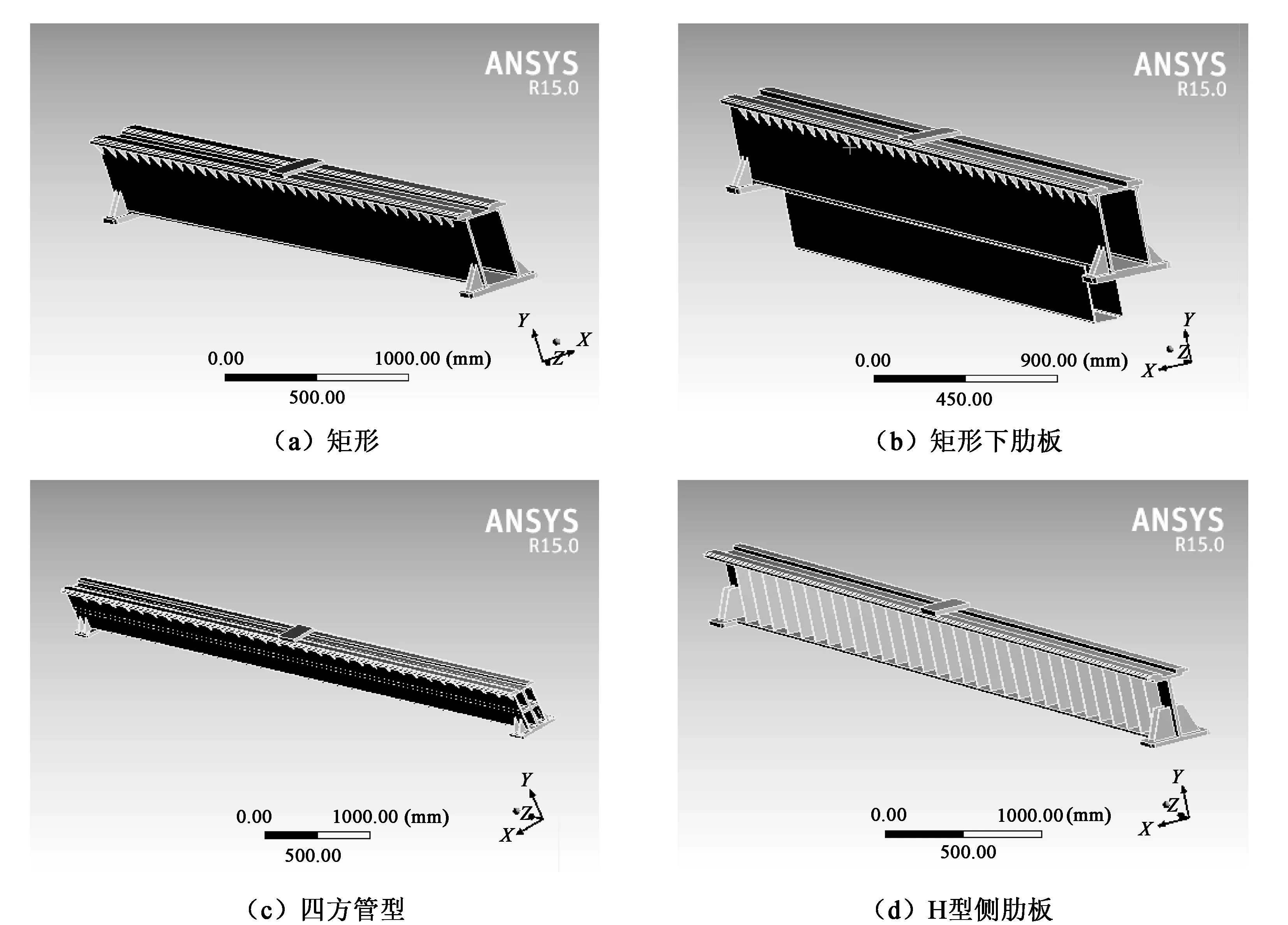
图4 不同截面的横梁仿真模型
2.2 材料属性及网格划分
由于设计了4种不同截面的横梁模型进行有限元静力学分析,其分析步骤都是一样的,所以下面只详细介绍其中一种模型的分析方法与思路,将其他三种模型的相应结果值罗列出。本文设计的横梁材料选用结构钢,其属性如表1所示。

表1 横梁的材料属性
网格划分质量对模型的分析结果影响很大。本文设计的不同截面模型,由于肋板和加强筋等不同结构存在,使整体模型复杂,所以采用自动划分方法对模型进行网格划分。为了保证分析结果的准确性,划分网格时,设置Element Size为50 mm,对如图3(a)中所示截面横梁结构进行网格划分后的结果如图5所示。

图5 网格划分结果
2.3 载荷的分析与施加
在静力学分析模块下,载荷必须根据实际情况加载到相应的部位,以保证分析结果的准确性[7-9]。横梁所受载荷分为以下两种:
(1)横梁自重
由于横梁截面形状和尺寸不同,加强筋和肋板的数量、位置不同,不同截面横梁的自重存在明显差异。通过在三维软件中建立的三维实体模型测算出的不同截面形状的横梁自重统计结果如表2所示。
(2)外加载荷
根据已知条件,横梁所受的外加载荷简化为300 kg的集中力,其作用点位于横梁长度方向的中点位置时,横梁的变形量最大。
当滑块1与滑块2移动到指定位置后,其两端在导轨上不运动。所以,在进行静力学分析时将横梁左右两端面固定,并将载荷施加在导轨上部的方块上,方向沿Y轴负方向。

表2 不同截面的横梁自重统计
3 大跨度梁的有限元分析结果
在有限元软件中,得到的不同截面横梁的分析结果如图6所示。由于有限元分析结果中云图较多,图6中仅展示模型在1.0(True Scale)状态下的整体变形云图[10-11]。

图6 不同截面横梁的变形云图
由图6横梁整体变形云图可以看出,横梁最大变形处在中点位置,且四方管型截面模型的变形量最大,矩形下肋板截面模型变形量最小。4种不同截面横梁模型加载求解结果统计如表3所示。
表3中所统计的4种截面模型的等效应力均在许用应力范围之内;由表2和表3可知矩形截面横梁自重最小,但其变形量最大;矩形下肋板截面横梁自重略大于矩形钢截面模型,但是矩形下肋板截面横梁的变形量远远小于矩形钢截面模型。综上所述,4种截面形状的横梁中,采用矩形下肋板钢横梁型截面作为大跨度梁的结构设计方案更为合理。利用有限元分析中的响应曲面优化模块的多目标优化方法,对矩形下肋板截型方案中的下肋板形状进行优化,优化的结果:下肋板长250 mm、宽120 mm、厚4.25 mm的矩形钢结构效果最好。按照此截面形式设计加工的梁的实物过程照片如图7所示。

表3 不同截面横梁的求解结果

(a)导轨面加工后的梁 (b)装配导轨后的梁图7 梁的实物照片
4 结 论
本文结合实际工程设计要求,设计了一种测量设备的龙门式主体结构,以其中的最大跨度横梁为研究对象,提出了4种不同截面形状的大跨度梁结构,建立了不同截面梁的三维模型,通过建立的力学模型计算出单一矩形截面的最大挠度≤2 mm。利用三维软件对不同截面的横梁结构进行了加强处理,在横梁上侧面布置导轨安装面、加强筋和肋板,对横梁不同截面进行了具体设计,构建出横梁的详细结构,通过有限元方法对比了不同截面横梁的自重和加载之后的静力学特性,对比结果显示:矩形下肋板截型的横梁结构方案最优。本文的设计过程解决了大跨度梁的实际工程问题,并为同类问题的解决提供了参考。
