Nano Fluid Flow Analysis in the Presence of Slip Effects and Wall Properties by Means of Contraction and Expansion∗
2018-09-10HinaSadafandRabiaMalik
Hina Sadafand Rabia Malik
1DBS&H,CEME,National University of Sciences and Technology,Islamabad,Pakistan
2Department of Mathematics and Statistics,International Islamic University,Islamabad 44000,Pakistan
AbstractThe present article is a study of mixed convective peristaltic flow of Cu-blood nano fluid confined in a non-uniform tube along with the velocity slip conditions and wall properties.Endoscopic or catheterized special effects are also taken into description.Upon utilization of the large wavelength and small reynolds number approximation,the non-dimensional governing differential equation took a more simplified form,which is then solved for the exact solutions.Afterwards,these outcomes are o ff ered graphically and are debated in detail.Velocity pro file for pure blood as well as Cu-blood and no-slip and slip effects are also discussed separately.Streamlines pattern is also discussed for different physical parameters.
Key words:peristaltic flow,exact solution,viscous nano fluid,mixed convection,velocity slip conditions,nonuniform tube,endoscopic tube,wall properties
1 Introduction
The term peristalsis is related to the Greek word peristaltikos,which defines compressing and clasping.The peristaltic passage is a device of fluid flow,which takes place due to the circulation of wave trains along the walls of tube/channel.In physical situations the prohibition of pumping machinery makes this mechanism indispensable.In general,its occurrence depends on the pressure difference variations.Pumping of bio fluids through this mechanism can be observed in many physiological systems,e.g.,lymph movement in lymphatic vessels, fluid mechanics in perivascular space of brain,chyme movement in intestinal tract,urine transport through the ureter,swallowing of food through esophagus and sperm transport in male reproductive tract etc.These peristaltic pumps are also widely used in industry and medicine,for example,to transport aggressive or corrosive fluids and for dialysis etc.From above explanation of the peristaltic transport mechanism,it is clear that the contaminations taking place due to direct contact with the external environment can be avoided by utilization of this mechanism.This advantage was convenient enough to encourage engineers to design various industrial devices using this mechanism like,hose pumps,pumps utilized to transport of corrosive and sensitive fluids in nuclear industry,roller/ finger pumps and heart-lung and dialysis machines etc.The relevance about the physiological applications of peristalsis was mainly given by Kill’s[1]research work.After some time,Latham[2]and Shapiro et al.[3]presented earliest peristaltic transport models for fluid motion.After above mentioned pioneering work,many researchers tended to explore the behavior of peristalsis by considering different aspects.[4−10]
Lately,a new branch of fluid mechanics namely“nano fluid dynamics” has emerged into spotlight which has diverse applications in the field of energy,medical science and process systems engineering.Nano fluids are engineered by suspending nanometer-sized particles in the base fluid such as water,propylene-glycol,emulsions,lubricants,coolants,bio fluids,oil and silk fibroin to enhance thermal conductivity of the fluid.Although,the great Scottish theoretical physicist,James Clerk Maxwell proposed the concept of nano fluids initially in 19th century,however,the term “nano fluid” was introduced after more than a century by Choi.[11]After,Choi[11]laid first stone in the field of nano fluids many researchers intended to explore this area of research.[12−16]
Recently,the peristaltic flow of nano fluids gained significant attention in biomedical engineering,most particularly in hyperthermia,drug delivery schemes and cryosurgery as a way to annihilate the undesired tissues in cancer therapy.The study of peristaltic flow of nano fluids by adopting Buongiorno model through a channel is carried by Tripathi and B´eg[17]under the approximations of long wavelength and low Reynolds number.Zeid[18]studied the combine effects of radiation,viscous dissipation and peristaltic motion of non-Newtonian nano fluid with heat transfer in an asymmetric channel while using the long-wavelength assumption.Sreenadh et al.[19]assumed the small reynolds number and elongated wavelength ap-proximations along with the asymmetric channel to scrutinize the peristaltic transport of nano fluid while taking into account the slip effects.Reddy and Makinde[20]explored the peristaltic flow of Jeffrey nano fluid through an asymmetric channel while considering the combined effects of buoyancy forces,magnetic field,thermophoresis and Brownian motion.Their research revealed that with an upsurge in the power of magnetic field velocity and nanoparticles concentration decrease while the temperature increases.Ghasemi[21]adopted the differential transformation method to determine the highly accurate analytical solution for the peristaltic nano fluid flow in drug delivery systems in the presence of thermophoresis and Brownian motion effects.Sucharitha et al.[22]obtained the exact and numerical solutions for the problem of peristaltic flow of nano fluid confined in a uniform or in a nonuniform porous channel in the presence of Joule heating and wall flexibility.Their key findings revealed that for uniform channel velocity is low as compared to the diverging channel but,opposite effects can be seen for the temperature and concentration fields.The exact solutions for the combined effects of wall properties and variable viscosity on the peristaltic flow of single wall carbon nanotubes are determined by Shahzadi et al.[23]
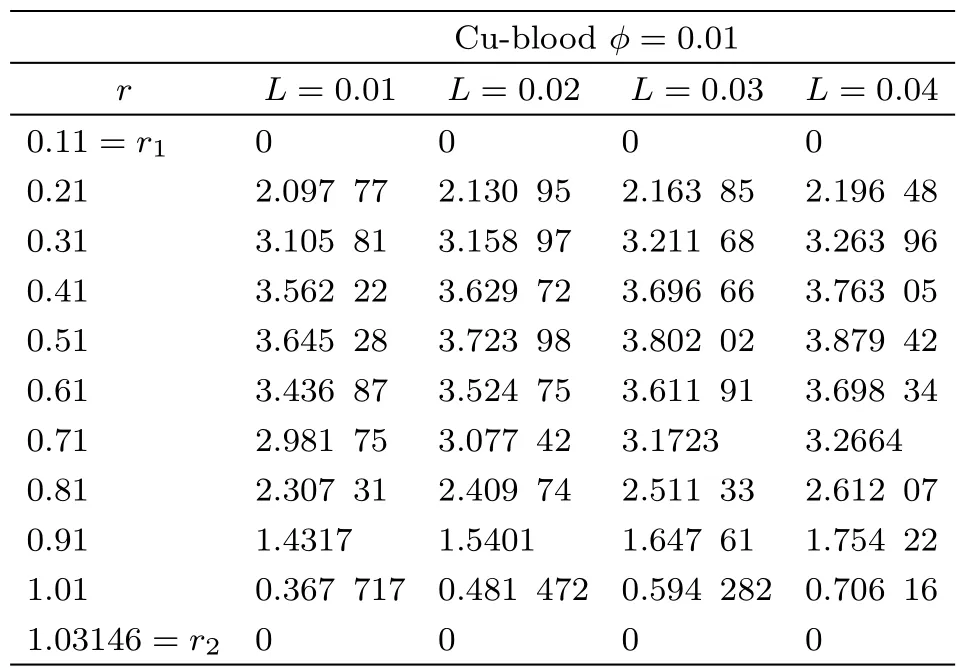
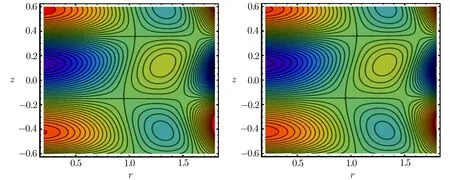
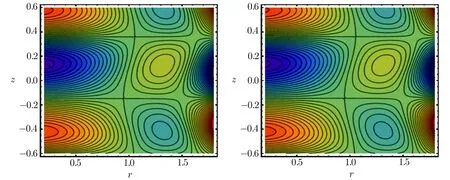
Some new dynamic features come into view when nano/micro scaled fluidic devices are concerned due to direct contact between the solid surfaces of the fluid container and the fluid constituent.Investigations suggest that for the nano/micro scale fluid flow no-slip condition near walls is not true,however,a certain degree of tangential slip must be considered.Applications regarding no-slip conditions include the polishing of the optical coatings,artificial heart valves and internal cavities,refrigeration equipment,inexpensive lubricating and many industrial processes.After pioneering work done by Navier,[24]Choi et al.[25]and Matthews and Hill[26−27]many researchers are seemed to be paying more attention to this phenomenon.[28−30]Khan et al.[31]discussed numerical study of partial slip on the MHD flow of an oldroyd 8-constant fluid.They concluded the result that the increase of the partial slip parameter,reduced the boundary resistance that leads to the increase of the velocity over the whole cross section.Derek et al.[32]explained experimentally that the fluid shows non-continuum effects such as slip flow when the molecular mean free path length of the fluid is comparable to the distance between the plates as in nano channels or micro channels.Renksizbulut et al.[33]explained the slip- flow and heat transfer in rectangular microchannels with constant wall temperature.They explained that the knudsen number is a measure of the degree of rarefaction,when lies in the range 10−3 The aforementioned work motivates us to venture the untouched regime of mixed convective peristaltic transport of Cu-blood nano fluid confined in non-uniform tube with slip and wall properties under large wavelength and low Reynolds number approximations.Due to slip effects non-continuum flow occurred at the peristaltic wall,also we are assuming flow motion for peristaltic problem so channel length is considered large.The exact solutions of the governing coupled differential equations will be obtained for nanoparticle temperature,nanoparticle velocity and stream function.These results will be then plotted and discussed at length. We have assumed the peristaltic flow occurrence for the two-dimensional incompressible viscous fluid in an annulus in the presence of nanoparticles,velocity slip and wall properties effects are also occupied.The equations for mass conservation,momentum and energy equations along with nanoparticles are defined as Fig.1 Flow geometry. The suitable boundary conditions for flow geometry(see Fig.1)are defined as[14,36−37] The leading equation of motion of the elastic wall may be specified as[22−23] Here σ is the elastic tension in the membrane,m is the mass per unit area,C′is the viscous damping forces.coefficient,p0is the pressure on the exterior surface of the wall owing to tension in the muscle,which is supposed to be zero here. Introduce the following dimensionless variables where d,Gr,B,L,E1,E2,E3denote for wave speed,Grashof number,heat absorption,velocity slip paramete,rigidity parameter,sti ff ness parameter,viscous damping force parameter respectively.Invoking Eq.(9)into the Eqs.(1)–(8),smearing the conventions of the small Reynolds number and large wavelength approximation,dipping the terms comprising Re,δ and greater we arrived at the following equations where Equation(10)specifies that p is independent of r and the dimensionless boundary conditions can be inscribed as The exact solution of the Eqs.(11)and(12)along with boundary conditions(14)is straight forward written as C3and C4are obtained by using boundary condition(14)and the stream function relation can be defined as u=−(1/r)((∂ψ)/(∂z)),w=(1/r)((∂ψ)/(∂z))at r=r2,whereas constants and G(z,t)are defined in appendix,and thermo physical properties are defined in Table 1. Table 1 Thermo-physical properties of fluid and nanoparticles. In order to perceive the assessable effects of numerous parameters convoluted in the study,the velocity,temperature and stream functions are designed for numerous values of the physical parameters.Tables 2 and 3 are considered to see the impact of velocity pro file for diverse values of nano particle volume fraction for both cases(velocity slip and no slip).It is portrayed from Tables 2 and 3 that velocity pro file gets a decreasing function when we insert nanoparticles into our base fluid for both cases e.g.velocity slip and no slip. Table 2 Velocity pro file for no slip flow for diverse values of ϕ with other fixed values of b2=0.24,λ =0.02,ϵ=0.05,z=0.22,r1=0.11,Gr=2.5,E3=1.5,t=0.12,k=0.16,E2=1.3,B=0.8,E1=1.5. Table 3 Velocity pro file for slip flow for diverse values of ϕ with other fixed values of b2=0.34,λ =0.02,ϵ=0.05,z=0.22,r1=0.11,Gr=2.5,E3=1.5,t=0.12,k=0.16,E2=1.3,B=0.8,E1=1.5. Table 4 Velocity pro file for no slip flow for diverse values of ϕ with other fixed values of b2=0.24,λ =0.02,ϵ=0.05,z=0.22,r1=0.11,Gr=2.5,E3=1.5,t=0.12,k=0.16,E2=1.3. Table 5 Velocity pro file for no slip flow for diverse values of ϕ with other fixed values of b2=0.24,λ =0.02,ϵ=0.05,z=0.22,r1=0.11,Gr=2.5,E3=1.5,t=0.12,k=0.16,E2=1.3. Tables 4 and 5 show the velocity pro file for swelling values of L(slip parameter)for both cases pure blood as well as Cu-blood case.It is depicted that with the rise of L(partial slip parameter),the velocity gradient for both pure blood as well Cu-blood falls,and hence the velocity pro files become flatter due to the reducing shear force from the slip boundary.Moreover,by the increase of slip parameter L,the main result appears to be that the reduced boundary resistance leads to the increase of the velocity pro file over the whole cross section(that agrees with Ref.[31]).Figures 2(a)and 2(b)are designed to see the impact of heat absorption parameter and volume fraction of the nanoparticle on the temperature pro file.It is depicted from Fig.2(a)that by increasing values of heat source parameter,temperature pro file gets an increasing behavior(Metabolic process is one of the best heat source tool in the human body).Figure 2(b)is plotted to see the impact of nano particle volume fraction on the temperature pro file.Temperature pro file diminutions when we increase nanoparticle into our base fluid.This is owing to the fact that high thermal conductivity of the nanoparticles shows a significant role for rapid dissipation this leads to the results that the use of the nanoparticles in different type as a coolant. Fig.2 (Color online)Nanoparticle temperature pro file for diverse values of B and ϕ with other fixed values of b2=0.34,λ =0.22,ϵ=0.15,z=0.22,r1=0.11,t=0.12,k=0.34. Fig.3 (Color online)Velocity pro file(a)for E2=1.5,(b)for E1=1.5,b2=0.34,λ =0.02,ϵ=0.05,z=0.22,r1=0.11,t=0.12,k=0.16,Gr=2.5,B=0.8,E3=1.55. Fig.4 (Color online)Velocity pro file(a)for Gr=2.5,(b)for E3=1.5,b2=0.34,λ =0.02,ϵ=0.05,z=0.22,r1=0.11,t=0.12,k=0.16,E2=1.3,B=0.8,E1=1.5. Figures 3(a)and 2(b)are prepared to inspect the effects of embedded parameters such as rigidity parameter,sti ff ness parameter,viscous damping force parameter and Grashof number on the velocity pro file for both cases(pure blood and Cu blood).It is portrayed in Figs.3(a)and 2(b)that by increasing values of rigidity and sti ff ness parameter,velocity pro file gets an increasing function for both cases(pure blood and Cu blood).Basically,the wall properties provides less resistance to the flow,thus velocity increases.It is also depicted from these figures,velocity pro file for pure blood case gets the larger curves as equated to Cu-blood case.Figure 4(a)are planned to perceive the impact of viscous damping force parameter on velocity pro file.Velocity pro file decreases due to increase in viscous damping force parameter for pure blood as well as Cu-blood case.Velocity pro file for swelling values of Grashof number for pure blood as well as Cu-blood is displayed in Fig.4(b).Buoyancy forces plays a dominant role as compare to the viscous damping force parameter,this contributes in enhancing velocity pro file for pure blood as well as Cu-blood case.One depiction from these figures is that velocity pro file closer to the endoscopic duct gets closer curves whereas,near the peristaltic wall more variation is seen.Trapping is stimulating occurrence,whereby a bolus is elated at the wave speed and this trapped bolus pushed onward along the peristaltic wave.Figures 5–7 are drawn to see the impact of rigidity parameter,sti ff ness parameter and viscous damping force parameter on trapping phenomenon.It is obviously understood from Figs.5(a)–5(b)that number of the trapped boluses as well as size of the trapped bolus remains same.It is evident from the Figs.5(a)–5(b)quantity of the trapped bolus remains same but magnitude,of the trapped bolus slightly decreases.It is also depicted from the stream Figures 6(a)–6(b),no change is observed from these plots when we upsurge the value of viscous damping force pa-rameter. Fig.5 (Color online)Stream plots for diverse values of E1with fixed values of λ =0.02,b2=0.34,E2=1.5,ϵ=0.05,z=0.34,r1=0.11,t=0.12,k=0.16,Gr=2.5,B=0.8,E3=1.55.(a)E1=1.1,(b)E1=1.5. Fig.6 (Color online)Stream plots for diverse values of E2with other fixed values of b2=0.34,λ=0.02,E1=1.5,ϵ=0.05,z=0.34,r1=0.11,t=0.12,k=0.16,Gr=2.5,B=0.8,E3=1.55.(a)E2=1.1,(b)E2=1.5. Fig.7 (Color online)Stream plots for diverse values of E3with other fixed values of b2=0.34,E2=1.5,λ=0.02,ϵ=0.05,z=0.34,r1=0.11,t=0.12,k=0.16,Gr=2.5,B=0.8,E1=1.55.(a)E3=1.1,(b)E3=1.5. In the present study,we are deliberating the physiological fluid flow analysis for viscous nano fluid due to the combined effects of velocity pro file and slip effects.The main deduction can be brie fly as follows (i)Velocity pro file drops for swelling values of volume fraction of the nanoparticle for both cases(velocity slip and no slip case). (ii)Velocity pro file increases due to less resistance in the fluid for increasing values of rigidity and sti ff ness parameter. (iii)Temperature pro file declines with an upsurge in ϕ this justifies that the use of the copper nanoparticle plays a key role for coolant. (iv)Number of trapped bolus almost remains unchanged for rigidity parameter,sti ff ness parameter,viscous damping force parameter cases. Appendix2 Problem Formulation


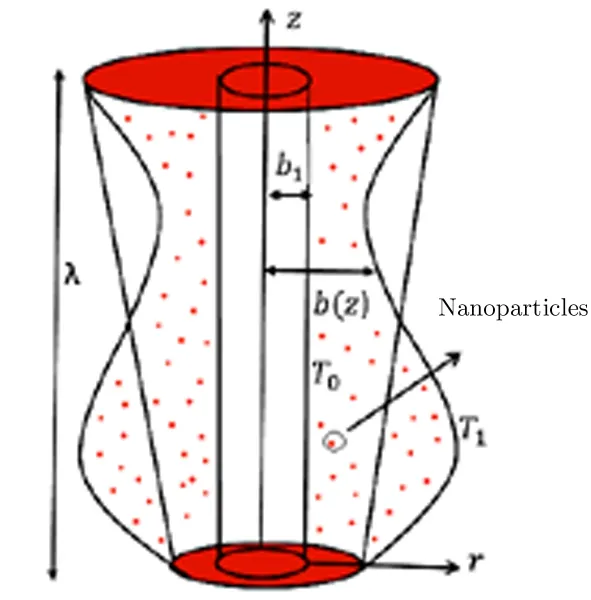


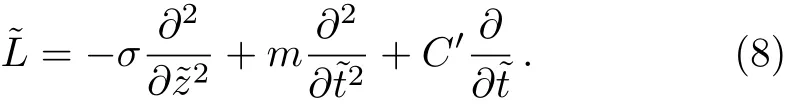

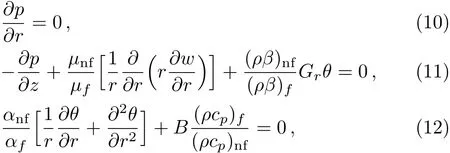

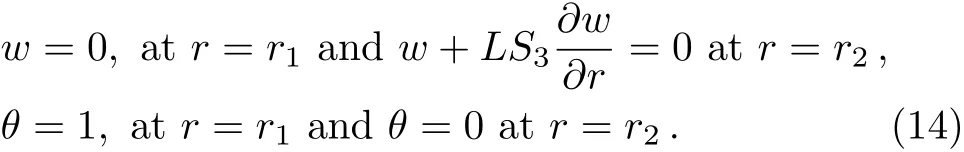
3 Technique of the Solution

4 Discussion of Results






5 Main Findings

杂志排行
Communications in Theoretical Physics的其它文章
- Vertical Sediment Concentration Distribution in High-Concentrated Flows:An Analytical Solution Using Homotopy Analysis Method
- Significance of Darcy-Forchheimer Porous Medium in Nano fluid Through Carbon Nanotubes
- Third-Order Optical Nonlinearity in Two-Dimensional Transition Metal Dichalcogenides∗
- Improving the Performance of Practical Decoy-State Measurement-Device-Independent Quantum Key Distribution with Biased Basis Choice∗
- Cylindrical Three-Dimensional Dust-Ion Acoustic Propagation in Plasmas
- Quadruple Gaussian Laser Beam Pro file Dynamics in Collisionless Magnetized Plasma
