Universal Pseudo-PT-Antisymmetry on One-Dimensional Atomic Optical Lattices∗
2018-09-10XinWang王欣andChangPuSun孙昌璞
Xin Wang(王欣) and Chang-Pu Sun(孙昌璞)
1Beijing Computational Science Research Center,Beijing 100193,China
2Graduate School,China Academy of Engineering Physics,Beijing 100193,China
AbstractWe present the interesting result that under sinusoidal field detuning setting along the propagation direction of 1D atomic lattices,the probe susceptibility response of the lattices,regardless of atomic configuration,uniformly demonstrates pseudo-PT-antisymmetry,which by our definition corresponds to n(z)= −n∗(−z),the complex refractive index antisymmetry along propagation axis,and when being cast back to quantum mechanical side,corresponds to V(x,t)= −V∗(x,−t),the conjugate time-reversal antisymmetry of complex potential.We define this as the pseudo-PT-antisymmetry,and prove the reason for this phenomenon to be the quantum-mechanical nature described by master equation under weak field approximation for any configuration of 1D atomic lattices.This work will help to deepen the understanding of origin of optical response features of atomic lattices,and will certainly open up the gate to a more rigorous,durable and flexible method of atomic optical lattice design.
Key words:pseudo-PT-antisymmetry,conjugate time-reversal antisymmetry,zigzag-type atom configuration
1 Introduction
Since the concept of PT-symmetry was raised by Bender and co-workers,[1−2]in the past decade there has been growing interest in the study of this area due to the fact that non-Hermitian PT-symmetric Hamiltonian extends the framework of quantum mechanics into the complex domain.Although in recent years much work has been done on the theoretical side of this issue,[3−12]up till this day,there has not been genuine experimental realization of PT-symmetric quantum system yet,because the PT-symmetry requires V(x)=V∗(−x)for one-dimensional Hamiltonian,which demands existence of complex potential for the system,something hard to realize despite the theoretical proposal.
Fortunately,the study of PT-symmetry found its cast in the field of optics,thanks to the isomorphism between Schrödinger equation and optical paraxial wave equation.For this reason,many endeavors have shown up in realizing PT-symmetric optical metamaterials in recent years. On one hand,artificial optical materials have already shown the advantages for achieving unusual electromagnetic properties compared to natural media,not to mention the fact that the PT-symmetry will certainly open up the gate to more intriguing properties,like double refraction and band merging,[13−14]power oscillations,[15−16]coherent perfect absorbers,[17−19]unidirectional invisibility,[14,20−21]and so on.However as a matter of fact,most of these works are carried out on solid-state optical systems,without much attempt to utilize atomic lattices.Considering that atomic optical lattices have their big advantages in real-time,all-optical tunable and reconfigurable features in control as compared to solid-state systems,it is of valuable importance to extend the study of PT-symmetry to this area.In recent years several works have come into sight[22−26]on this aspect.
For study of PT-symmetry in optical field,when mapping the time-dependent Schrödinger equation to the paraxial wave propagation equation,the role of time variable t in Schrödinger equation is cast to the spatial variable of propagation direction(we use z in this work)in paraxial wave equation,and the PT-symmetry condition V(x)=V∗(−x)is mapped to the complex refractive index symmetry n(x)=n∗(−x)in transverse plane of propagation.Many works have been done under this scheme.[15−16,27−33]
On the other hand,the question has been asked about what if we implant the symmetric modulation of complex refractive index n to the longitudinal direction instead of transverse plane of optical wave propagation.[34]Inspired by this,we propose the scheme of realizing complex refractive index symmetry along the propagation direction of one-dimensional atomic optical lattices.
Surprisingly and most interestingly,in our study we find that under spatial sinusoidal detuning setting along propagation direction,1D atomic lattices of any configuration could uniformly demonstrate pseudo-PT-antisymmetry,by which we mean n(z)= −n∗(−z),where z denotes the propagation axis.When being cast back to quantum-mechanical side,this corresponds to V(x,t)=−V∗(x,−t),the conjugate time-reversal antisymmetry of complex potential V(x,t)in Schrödinger equation.
The phenomenon of universal inducement of pseudo-PT-antisymmetry goes beyond our usual recognition that the optical features of atomic lattices are predominantly related to the energy level configuration of atoms,which together with particular setting of applied fields determine the optical response features of the lattice.Rather,it must originate from some fundamental physical features in the atomic optical lattice system,so that it could not see the difference between configuration details.And we find that the reason for this phenomenon is the quantummechanical nature described by master equation under weak probe field approximation.
The article is organized as follows.In Sec.2 we deif ne the concept of pseudo-PT-antisymmetry.In Sec.3 we give the proof of universal inducement of pseudo-PT-antisymmetry under spatial sinusoidal detuning setting.In Sec.4 we present an example of pseudo-PT-antisymmetry inducement on the family of zigzag-type configurations.And finally in Sec.5 we conclude the article.
2 Pseudo-PT-antisymmetry
The effects of parity operatorand time-reversal operatoron quantum-mechanical coordinate operatorand momentum operatorare
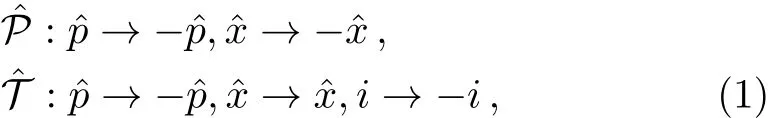

This suggests a complex potential setting,which is not normally applicable in physical experimental environment.However the complex potential V has found its cast in the complex refractive index n in optics.
Optical lattice can be looked on as non-magnetic medium with no free charges or currents in it,then for electric field propagation we have the Helmholtz equation
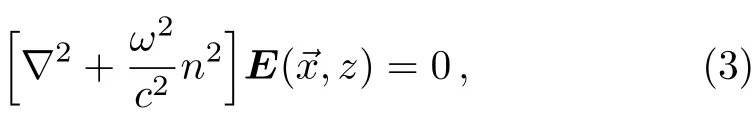
where z is the variable on propagation axis of 1D atomic lattices,stands for any vector in transverse plane,ω the angular frequency of the electromagnetic wave oscillation,and c the speed of light in vacuum.In homogeneous media,Eq.(3)reduces to a scalar equation.
In our one-dimensional optical lattice model,n could be designed as the periodic function of z,i.e.n(z+a)=n(z),where a is the spatial period of 1D optical lattice.Including the real background refractive index n0,we have n(z)=n0+δn(z),with δn(z)=nR(z)+inI(z)being complex and|δn(z)|≪ |n0|.The propagating electric field is given by E(x,z)= ϕ(x,z)eik0z,where ϕ(x,z)is the envelope function.Then under paraxial approximation,the scalar Helmholtz equation reduces to
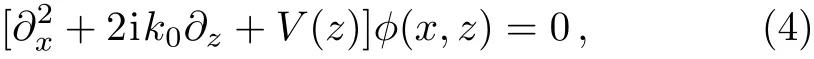
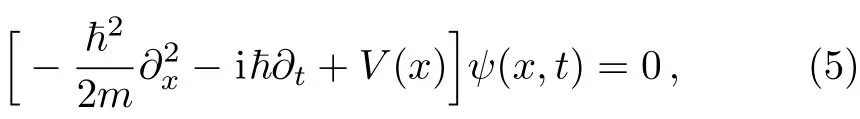
because the genuine analog requires that time variable t in Eq.(5)be cast to longitudinal variable z in paraxial wave equation,and spatial variable x in Eq.(5)be cast to transverse variable x,which is to say,V in Eq.(4)should be a function of x,not a function of z.This means the normal PT-symmetry requires the complex refractive index to satisfy δn(x)= δn∗(−x)in transverse plane,with no restriction set for z direction for 1D optical lattices.Compared to this,what we realized in this paper is δn(z)= −δn∗(−z)along the propagation direction of 1D atomic lattices.From the point of view of PT-symmetry,δn(z)= −δn∗(−z)corresponds to the condition

which is the conjugate time-reversal antisymmetry of complex potential V(x,t),and we call it pseudo-PT-antisymmetry.We expect the study on the optical side could eventually shed light on the quantum-mechanical side,for interest of investigating V(x,t)= −V∗(x,−t).
One may ask why in casting back the pseudo-PT-antisymmetry to Schrödinger equation,both variables x and t are included in potential V,while in Eq.(2)only variable x is shown.This comes from the features of 1D atomic optical lattices,which cause the difference between paraxial wave equation and Schrödinger equation in spite of the isomorphism.Since the atomic lattices are constructed by forming dipole traps to trap the atoms,there is density distribution in transverse plane,which affects the complex refractive index n,so n is not only function of z,but also x.However along the z axis of atomic optical lattices,settlement on any value of x does not affect the pseudo-PT-antisymmetry,so we can express n as n(z).
3 Universal Pseudo-PT-antisymmetry on One-dimensional Atomic Lattices
For any atomic configuration,the density matrix equations of o ff-diagonal terms can be expressed in the general form of master equation

The Hamiltonian can be written as,whereis the Hamiltonian of free atom,andthe interaction between atom and applied fields.Then since(En− Em)ρnm,the master equation becomes

On 1D atomic lattices,we are applying a weak field to probe the optical response.Compared to all the other strong coupling fields,this is a perturbation,therefore we can turn to the traditional perturbative calculation method in nonlinear optics to carry out our calculation.
First suppose all external fields are treated as perturbation,then from Eq.(7),we have the first and second order perturbed ρnmexpressed as
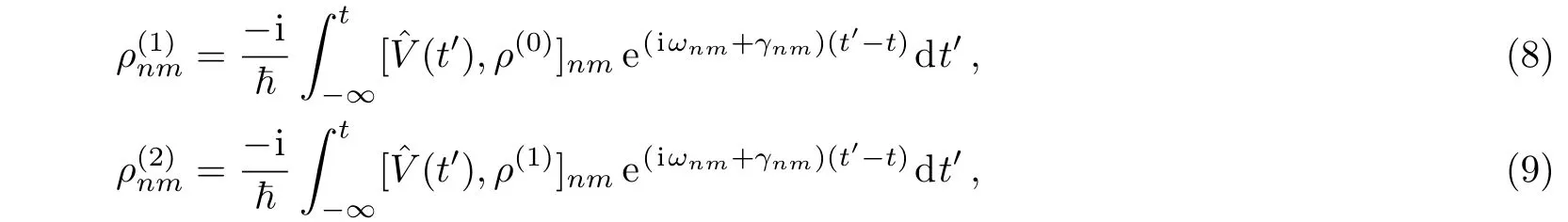
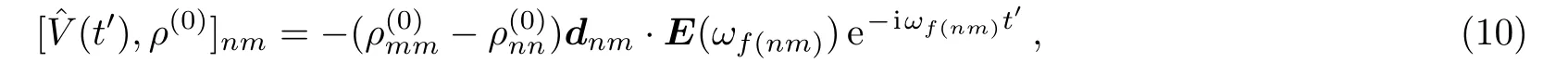
therefore
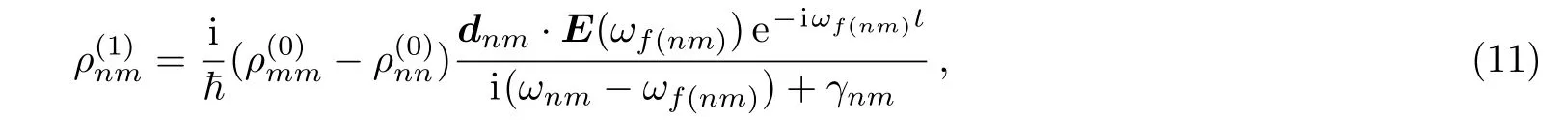
and we can derive from here

where N is the atomic distribution function.
To get the second order perturbed density matrix term,normally we should directly bring the result ofinto Eq.(9)for a second round calculation.But things get different here when using weak probe field approximation.Because the probe field is so small compared to the strong coupling fields,in the first round calculation of,we usually ignore the existance of the probe field.Then when calculating,we begin to include the effect of probe field.This is to say,thein Eq.(8)and Eq.(9)are different by an addition of probe field.And the optical response of the probe field is the difference between the originalwithout throwing in probe field

and that after throwing in the probe field

where under the assumption that the probe field is coupled to energy leveland


On the other hand,it is straightforward to get

since this is analogous to the expression in Eq.(10),comparing with following the same path we have
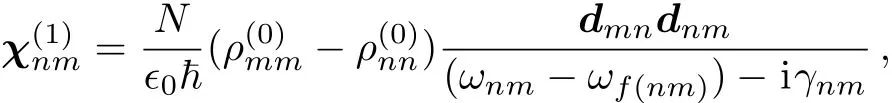

This is the expression of weak probe field susceptibility.Now we relate this to the spatial sinusoidal field detuning set.We get this idea from solving the zigzag-type configuration problems,which we will present as an example in the next section.We rewrite the above expression as

The part i(ωkl−ωf(kl))in the denominator is by definition the term i∆d,where∆dis the frequency detuning of the probe field.So in a generalized way,we can say that the denominator can be expressed as the polynomial in the indeterminate i∆din the form

knowing γklcan be looked on as γkl(i∆d)0.On the other hand,for the numerator,bothandare real numbers that can be expressed in form

which is a special case of Σj=0Aj(i∆d)j.Therefore we can say the expression of Eq.(14)is a special case of expression

where N1is the highest order of indeterminate i∆din the numerator’s polynomial,and N2the highest order of i∆din the denominator’s polynomial.If we can prove that the expression in Eq.(15)can have the universal pseudo-PT-antisymmetry,then it will also work on its special case,Eq.(14).
Equation(15)can be rewritten as
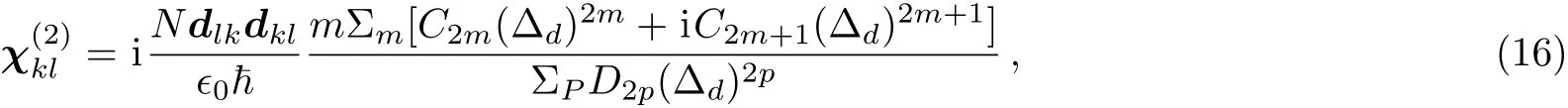
where C2m,C2m+1(m = 0,1,2,...)and D2p(p=0,1,2,...)are real coefficients from rearranged polynomials of Aj(j=0,1,...,N1)and Bl(l=0,1,...,N2).Normally for 1D atomic lattices,N=N(z)is the periodic Gaussian distribution function of the atom density,which can be expressed as
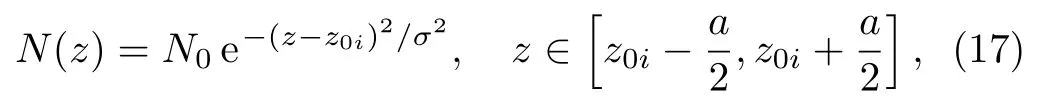
where z0iis the i-th lattice center,a the length of the lattice unit(also the spatial period of the 1D optical lattice),N0the density of atoms at lattice center,and σ the standard deviation of the Gaussian distribution.We can always choose an appropriate reference point z0(in this case,any z0i)to make N(z)an even function about z0.After that,it is straightforward to see that if we set the coupling field frequency detuning∆dto be a sine function of z axis,i.e.,
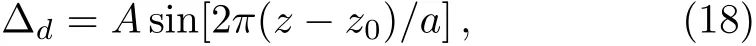
where A represents the real amplitude of the oscillation,then about the reference point z0along z direction,is an odd function andis an even function,which indicates the realization of pseudo-PT-antisymmetry n(z)= −n∗(−z).
We have proved that under spatial sinusoidal detuning setting,a probe field susceptibility described by Eq.(15)will demonstrate pseudo-PT-antisymmtry.Since under the weak probe field approximation,the probe susceptibility of 1D atomic lattices of any configuration can always be expressed by Eq.(14),a special case of Eq.(15),we have arrived at the conclusion that the sinusoidal detuning setting can induce universal pseudo-PT-antisymmtry on 1D atomic optical lattices,regardless of energy level configuration.
In the next section we will present an example of universal pseudo-PT-antisymmtry inducement on the zigzagtype configuration family of 1D atomic lattices,where we first found the idea of sinusoidal detuning setting in our early study,and where we got our first inspiration on the general case proof shown above.
4 Universal Pseudo-PT-Antisymmetry on Zigzag-Type Configuration Family:An Example
4.1 Case Study:N Configuration(i)The Model
We first point out that the control of n is eq uivalent to modulating probe susceptibility χp.and from Sec.2 we know that n=n0+δn with n0being the background refractive index,also for atomic optical lattices n0=1,so we have δn= χp/2.

Fig.1 (Color online)(a)Diagram of the four-level N configuration(4-zigzag),into which the atoms are driven by a weak probe field Ωpand two moderate coupling fieldΩcand Ωd.(b)An ensemble of cold87Rb atoms forming 1D optical lattice by being trapped at the bottom of periodically distributed dipole traps along z direction.The spatial period of the dipole trap distribution(and therefore the spatial period of atom distribution)is a.Within each dipole trap,we assume the atoms to be in Gaussian distribution,with σ being the standard deviation,as described by Eq.(17).
We design a system of one-dimensional optical lattice,composed of Gaussian-distributed bunches of cold87Rb atoms,with each bunch seated at the bottom of a dipole trap along z direction,and atoms coherently driven into N-type configuration by three coherent laser if elds applied to the system,at frequencies(amplitudes)ωp(Ep), ωc(Ec),and ωd(Ed),as shown in Figs.1(a)and 1(b).The N-configuration consists of two ground levelsandand two excited levelsandand the weak probe field ωpinteracts with the dipole-allowed transitionwhile the two strong pump fields ωcand ωdact upon transitionsandrespectively.The corresponding frequency detunings are defined asand the Rabi frequenciesandwith ωij= ωi− ωjbeing resonant transition frequencies and dijthe relevant dipole moments(i,j are labels of the energy levels).
With rotating-wave and electric-dipole approximations,the interaction Hamiltonian can be written as
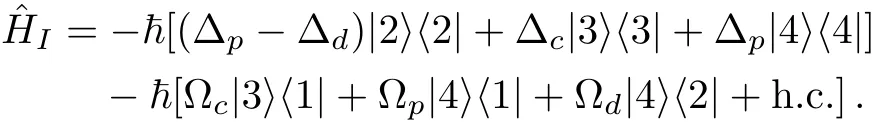
We then get the density matrix equations:

(ii)A Special Case of Pseudo-PT-Antisymmetry on N Configuration
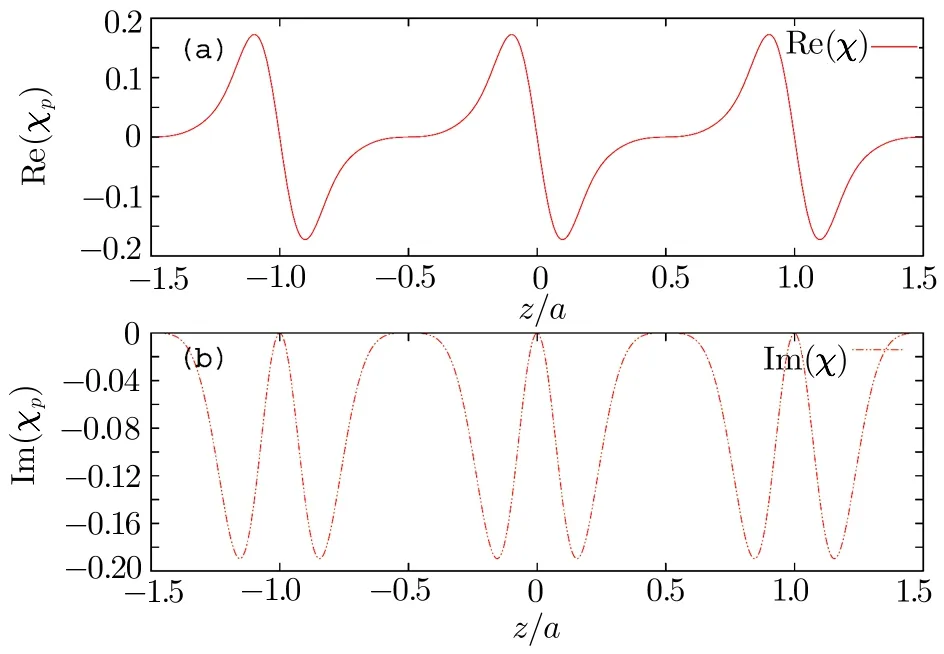
Fig.2 (Color online)The pseudo-PT-antisymmetry of χp(z)under condition of Eq.(18).(a)The real part of probe susceptibility Re[χp]for N configuration as function of z,with x axis in unit of z/a.(b)The imaginary part of probe susceptibility Im[χp]for N configuration as function of z,with x axis in unit of z/a.Here we set z0=0 and A=1 MHz in ∆d=Asin[2π(z− z0)/a],Ωc= Ωd=5 MHz,Ωp=0.06 MHz,and Γ31= Γ32=Γ41= Γ42=3 MHz.We take σ =0.2a in Gaussian distribution function of Eq.(17).
Using weak probe field approximation,we obtain the first-order steady-state solutions of Eqs.(19),and since we are interested in the probe field,we directly go for the expression of.For simplicity,we set γ12=0 and look at the special case

then obtain
Here we have uniformly replaced all the∆cby∆d,while still writing down Ωcand Ωdseparately.The reason of doing this will be explained later.
We can see that under the assumption that Ωc= Ωdare real numbers,both the numerator and the denominator of the formula can be expressed as polynomials in indeterminate i∆d,i.e.,


where N1is the highest order of term i∆din numerator,and N2the highest order of i∆din denominator.Aj(j=0,1,...,N1)and Bl(l=0,1,...,N2)are real coefficients determined by Eq.(21). The expression of Eq.(22)goes back to the form of Eq.(17),usingand setting N(z)to be the periodic Gaussian distribution function described by Eq.(17),we realize pseudo-PT-antisymmetry n(z)= −n∗(−z)for 1D optical lattice on N-configuration.
In Figs.2(a)and 2(b)we plot the real and imaginary parts of probe susceptibility χpas function of z.The parameters used here are Ωc= Ωd=5 MHz,Ωp=0.06 MHz,Γ31= Γ32= Γ41= Γ42=3 MHz.For the frequency detuning function∆d=Asin[2π(z−z0)/a],we choose z0=0 and set A=1 MHz.
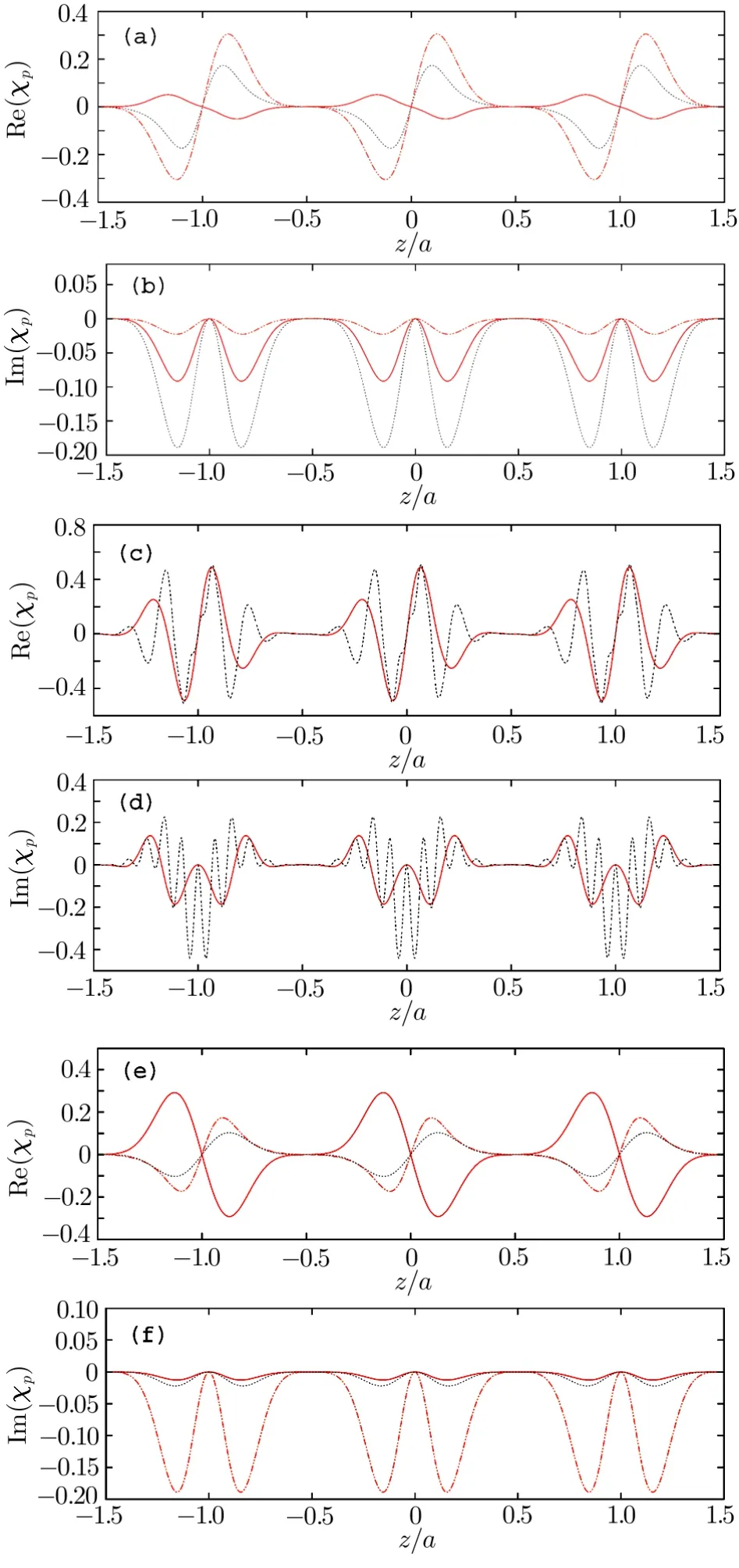
Fig.3 (Color online)(a)and(b)are the real and imaginary parts of χp(z)under different oscillation amplitudes of∆cand∆d.The red solid line corresponds to A1/A2=0.3,black dashed line corresponds to A1/A2=1,and orange dashed line corresponds to A1/A2=3 in Eqs.(23).(c)and(d)are the real and imaginary parts of χp(z)under different spatial periods of∆cand∆d.Red solid line corresponds to m=3,n=1,gray dashed line corresponds to m=5,n=7 in Eqs.(24).(e)and(f)are the real and imaginary parts of χp(z)under different values of Ωcand Ωd.Red solid line corresponds toΩc=3 MHz,Ωd=6 MHz,orange dashed line corresponds to Ωc=5 MHz,Ωd=5 MHz,black dashed line corresponds to Ωc=7 MHz,Ωd=2 MHz.All the other parameters are the same as in Fig.2.
(iii)Pseudo-PT-Antisymmetry on N Configuration under Modified Parameters
Setting∆c=∆din Eq.(20)ensures the expression of ρ14in Eq.(21)to be a function of indeterminate i∆d,however,loosening this condition to
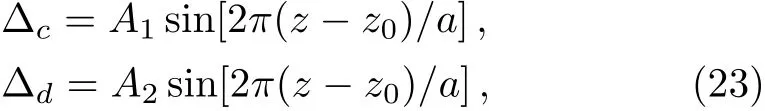
where A1≠A2are both real amplitudes,we still get the pseudo-PT-antisymmetry,as shown in Figs.3(a)and 3(b).
We can also modify the periods instead of amplitudes of the sine functions by setting
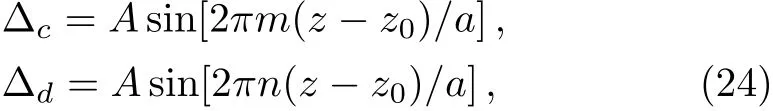
where m and n are different integers,and we get the modulated periodical spatial distribution of χp,which still satis fies the pseudo-PT-antisymmetry as shown in Figs.3(c)and 3(d).
For the condition Ωc= Ωdin Eq.(20),we change them to different values and still get the pseudo-PT-antisymmetry.The results are shown in Figs.3(e)and 3(f).
4.2 Numerical Study on Di ff erent Zigzag Con figurations
We now look at the different zigzag-type atom configurations as shown in Fig.4,on the same setting of optical lattice described by Fig.1(a).In Fig.4(a)we show the M-type zigzag configuration,which is the original N-type configuration spreading out one“leg” on the left-hand side to an additional ground level state(labeled|1⟩here).Figure 4(b)is the N-type configuration spreading out one“leg” on the right-hand side to an additional excited level(labeled|5⟩here),which we call W-type configuration.Combining these two,the N-type spreading out one “leg”to each side gives the six-level zigzag type in Fig.4(c).And lastly,adding one more“leg” on the right-hand side of six-level zigzag gives seven-level zigzag in Fig.4(d).
For convenient comparison between different configuration types,we assume that in and between each type:
(i)All the Rabi frequencies Ωciand Ωdi(i is integer)are of equal values.
(ii)All the lower level states are treated as ground states,and for integer i,j representing different ground states,γij=0.
(iii)Γij(i,j are different integers)only exists between adjacent excited and ground states that are coupled by external fields.
Notice that if we also include the N-type into the current group for comparison,we should set Γ32=0,which is different from the N-type setting previously used in this section.
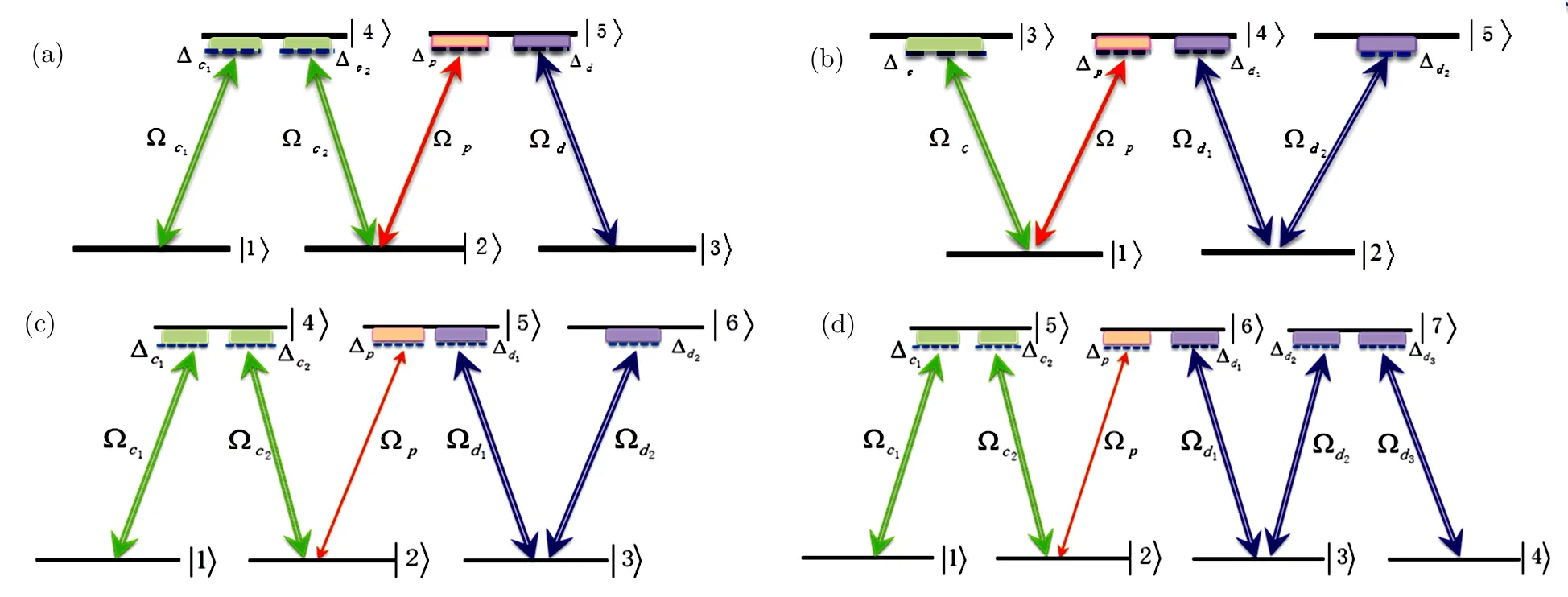
Fig.4 (Color online)(a)M-type zigzag configuration,which is N-type configuration spreading out one “leg” on the left-hand side to the newly added ground state labeled|1⟩.(b)W-type zigzag configuration,which is N-type configuration spreading out one “leg” on the right-hand side to the newly added excited state labeled|5⟩.(c)Six-level zigzag configuration,which is N-type configuration spreading out one “leg” on the left-hand side to the newly added ground state labeled|1⟩,and one “leg” on the right-hand side to the newly added excited state labeled|6⟩.(d)Seven-level zigzag configuration,which is six-level zigzag configuration spreading out one “leg” on the right-hand side to the newly added ground state labeled|4⟩.

Fig.5 (Color online)The pseudo-PT-antisymmetry of χp(z)on N-type(red solid line),M-type(green dashed line),W-type(blue dotted line),six-level zigzag(black dotted line)and seven-level zigzag(orange dashed line)atom configurations.(a)The real part of probe susceptibility Re[χp]for different atom configurations as function of z,with x axis in unit of z/a.(b)The imaginary part of probe susceptibility Im[χp]for different atom configurations as function of z,with x axis in unit of z/a.The parameters used here are Ωci= Ωdi=5 MHz,Ωp=0.06 MHz,Γij=3 MHz(when being nonzero term),∆ci= ∆di=Asin[2π(z− z0)/a]with z0=0 and A=1 MHz.The atom density distribution function is the periodic Gaussian function given by Eq.(17)and σ=0.2a.
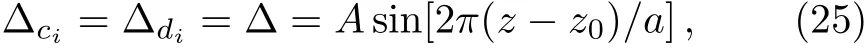
Following these setting,in drawing the plot of Fig.5,we set Ωci= Ωdi=5 MHz,Ωp=0.06 MHz,Γij=3 MHz whenever it is nonzero,and for the key role of coupling field detunings,we set and choose z0=0 and A=1 MHz.The periodic Gaussian distribution function of atom density on the optical lattice is still given by Eq.(17).The uniform inducement of pseudo-PT-antisymmetry on different zigzag-type atomic optical lattices are shown in Fig.5.
From Fig.5 we see that the N-type configuration has the largest amplitude in both real and imaginary parts of probe susceptibility χp.The M-type and W-type are both N-type spreading out one “leg”,one to an extra ground state,one to an excited state.Compared to N-type,the W-type has both the real and imaginary parts of χpsuppressed to a moderate level,while for the M-type,the real part of χpis also suppressed largely but less than the W-type,however the imaginary part is suppressed almost to zero.The six-level zigzag configuration is the W-type spreading out one“leg” to an extra ground state,and the seven-level zigzag configuration is the six-level configuration spreading out one more“leg” to a ground state on the other side.Compared to the W-type,the real part of χpof six-level configuration is strongly suppressed,but that of seven-level is strongly enlarged.On the contrary,the imaginary part of χpof six-level configuration is strongly enlarged,and that of seven-level is strongly suppressed.We leave the detailed and systematic study of the correlation between the atom configuration and probe susceptibility to the future work.
5 Conclusions
In this paper,we show the result that under the setting of sinusoidal spatial distribution of coupling field detunings,the pseudo-PT-antisymmetry,i.e.δn(z)=−δn∗(−z),the complex refractive index antisymmetry along propagation direction of 1D atomic lattices,can be universally induced on the 1D atomic lattices of any configuration.
We find that the reason for the uniform inducement of pseudo-PT-antisymmetry is rooted in the quantummechanical nature of atom- field interaction,which can be derived directly from the general form of master equation under weak probe field approximation.
Forfutureinterestoftheuniversalpseudo-PT-antisymmetry,we also point out that when being cast back to quantum-mechanical side,δn(z)= −δn∗(−z)corresponds to V(x,t)= −V∗(x,−t),the conjugate timereversal antisymmetry of complex potential V(x,t)in 1D Schrödinger equation.
In conclusion,the universal inducement of pseudo-PT-antisymmetry is a novel observation.It expands our understanding of the origin of optical response of atomic lattices,provides more reliable and variable method in designing atomic optical lattices,and o ff ers more flexibility and stability to the optical features of atomic lattices.
Acknowledgements
X.Wang would like to thank Jilin University and Center for Quantum Sciences of Northeast Normal University,where this work was first started.
猜你喜欢
杂志排行
Communications in Theoretical Physics的其它文章
- Vertical Sediment Concentration Distribution in High-Concentrated Flows:An Analytical Solution Using Homotopy Analysis Method
- Significance of Darcy-Forchheimer Porous Medium in Nano fluid Through Carbon Nanotubes
- Third-Order Optical Nonlinearity in Two-Dimensional Transition Metal Dichalcogenides∗
- Nano Fluid Flow Analysis in the Presence of Slip Effects and Wall Properties by Means of Contraction and Expansion∗
- Improving the Performance of Practical Decoy-State Measurement-Device-Independent Quantum Key Distribution with Biased Basis Choice∗
- Cylindrical Three-Dimensional Dust-Ion Acoustic Propagation in Plasmas
