基于FPGA的图像畸变矫正研究
2018-09-10裴明敬符茂胜董文忠
裴明敬 符茂胜 董文忠
(皖西学院电子与信息工程学院, 安徽 六安 237012)
目前,图像畸变矫正技术多停留在理论研究阶段,在工业上的应用主要基于PC来实现。畸变矫正包括摄像机标定和矫正部分,其中标定部分比较复杂。当摄像机位置固定并且模组在同一水平面的情况下,只做一次标定即可,而矫正则需每次重复进行。畸变矫正过程涉及到图片的映射,映射是随机存储过程,处理比较耗时。在此,我们提出了一种新的矫正方法 —— 阵列点阵标定板法。为了达到更快的矫正速度,矫正部分也在FPGA(Field Programmable Gate Array,现场可编程门阵列)上进行硬件加速处理,这样可以分别将摄像机标定部分和矫正部分做成硬件加速模块,并结合FPGA并行处理,利用乒乓操作以及流水线等优势进行设计,从而实现图像实时处理。
1 相关理论
本次实验不采用物理标定版,而是在LCD屏幕中生成pattern标定图,然后通过摄像机采集得到畸变图。通过pattern标定图的已知信息,可以得到畸变图的信息,在畸变图和pattern图之间建立映射关系,就可以计算出畸变参数。传统的畸变算法比较复杂,实时性差,其主要作用在于实现非线性变换[1-3]。
通过透视变换将空间中的点投影到图像平面即形成视图,投影公式如下:
S·m′=A·[R|t]·M′
(1)
(2)
式中:S为摄像机平面空间,以(X,Y,Z)为某一点的世界坐标;(u,v)为点投影在图像平面的坐标;以像素为单位,A被称作摄像机矩阵,或者内参数矩阵;(cx,cy)为基准点,通常在图像的中心;fx、fy为以像素为单位的焦距。如果针对摄像机所拍的某幅图像进行升采样或者降采样,参数fx、fy、cx,cy都将缩放同样比例。内参数矩阵不依赖于场景视图,只需固定焦距即可,矩阵计算数据可以重复使用。旋转-平移矩阵[R|t]为外参数矩阵,用于描述摄像机相对于某个固定场景的运动轨迹,或者场景相对于摄像机的运动轨迹。如果场景围绕摄像机作刚性运动,也就是[R|t]将点(X,Y,Z)的坐标变换到某个坐标系,这个坐标系相对于摄像机来说是固定不变的。真正的镜头通常有一些形变,主要的变形为径向形变,也会有轻微的切向形变。模型可以扩展为:
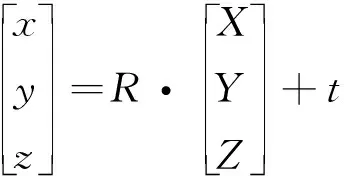
(3)
x′=x/z
y′=y/z
(4)
x″=x′(1+k1·r2+k2·r4)+2p1x′y′+
p2(r2+2x′2)
(5)
y″=y′(1+k1·r2+k2·r4)+2p1x′y′+
p1(r2+2x′2)
(6)
r2=x′2+y′2
u=fx·x″+cx
v=fy·y″+cy,
式中:k1和k2是径向形变系数,p1和p2是切向形变系数。
根据以上模型来完成以下步骤:
(1) 给定内参数和外参数,将点投影到图像平面。
(2) 给定内参数,根据几个点坐标和其对应的图像坐标计算外参数。
(3) 根据已知的定标模式,从几个角度的照片来计算摄像机的外参数和内参数,运用最小二乘法估计相关参数[4-5]。
2 系统设计
2.1 系统标定方案
设计系统标定总体方案。图1所示为标定方案总体框图。这是针对畸变矫正效果要求非常苛刻的情况所作的设计。标定只需要做一次,标定时间很长,但是整个系统对一次标定的时间并不是非常敏感,故考虑在下层实现标定。
方案总体包括二值化角点粗提取、腐蚀和膨胀、Blob分析、外参摄像机标定、坐标生成和坐标映射等部分,各部分均挂在系统总线上,与微处理器相互交换数据。

图1 标定方案总体框图
摄像机标定步骤如下:
(1) 找棋盘标定板平面中的角点。在此过程中,要保证角点数目正确,精确到每行、每列各多少个点,不能多检或漏检。此步骤只是粗略提取角点,如果精度不高,矫正效果就会严重受损。
(2) 对角点进行提取,保证达到亚像素级别。
(3) 按照一定规则对角点进行排序。
(4) 计算角点的世界坐标系和图像坐标系,对内外参数进行初始化。
(5) 计算摄像机单应性矩阵等内部参数,对单应性矩阵归一化处理,利用最小二乘法原理计算出4个内参数。
(6) 利用畸变模型求解畸变参数,然后利用非线性最小二乘法进行参数优化。
(7) 计算外参数。根据内参数、畸变参数和已知点分别求解畸变坐标、单应性矩阵、旋转矩阵和平移矩阵,然后通过高斯-牛顿法对旋转矩阵和平移矩阵进行优化提炼(大约进行20次迭代),每次迭代都需要进行一次投影映射变换。
(8) 利用高斯-牛顿方法对所有的参数进行优化提炼,迭代30次,以最后一次的结果作为最终参数值。
本方案基于FPGA平台来实现标定,系统从上层发出指令,在下位机进行标定。当接收到命令后,系统会立即进行图片采集,并将图片送入下位机进行标定,然后分别计算出内参数、外参数和畸变参数。此过程只需要进行一次标定,后期只需进行矫正即可。
2.2 畸变矫正
当下位机计算出参数之后,立即进入畸变矫正过程。在此过程中,将原始图像按照一定大小分块,并通过畸变模型找出畸变图中对应块的大小,然后进行坐标映射。考虑到FPGA资源情况,选择了8个图像块同时进行处理,这样可以大大缩短矫正时间。
畸变矫正的理想图分辨率为6 576× 4 384,畸变图分辨率为6 576×4 384。将理想图按照行列自行分块,每块大小为822×548。横向分为8个块,纵向分成8个块,一共64个块。
分块后,通过畸变模型计算出原始畸变图中的畸变块,然后计算出畸变块的外接矩形,将畸变图外接矩形作为畸变图的分块。图2所示为原始图像到目标图像的映射过程。blockij模块中的像素坐标,通过畸变模型计算的坐标在畸变图外接块中进行插值,将计算处理的像素值返回,赋值给blockij模块中像素坐标对应的像素值。为了缩短处理时间,采用模块并行操作。
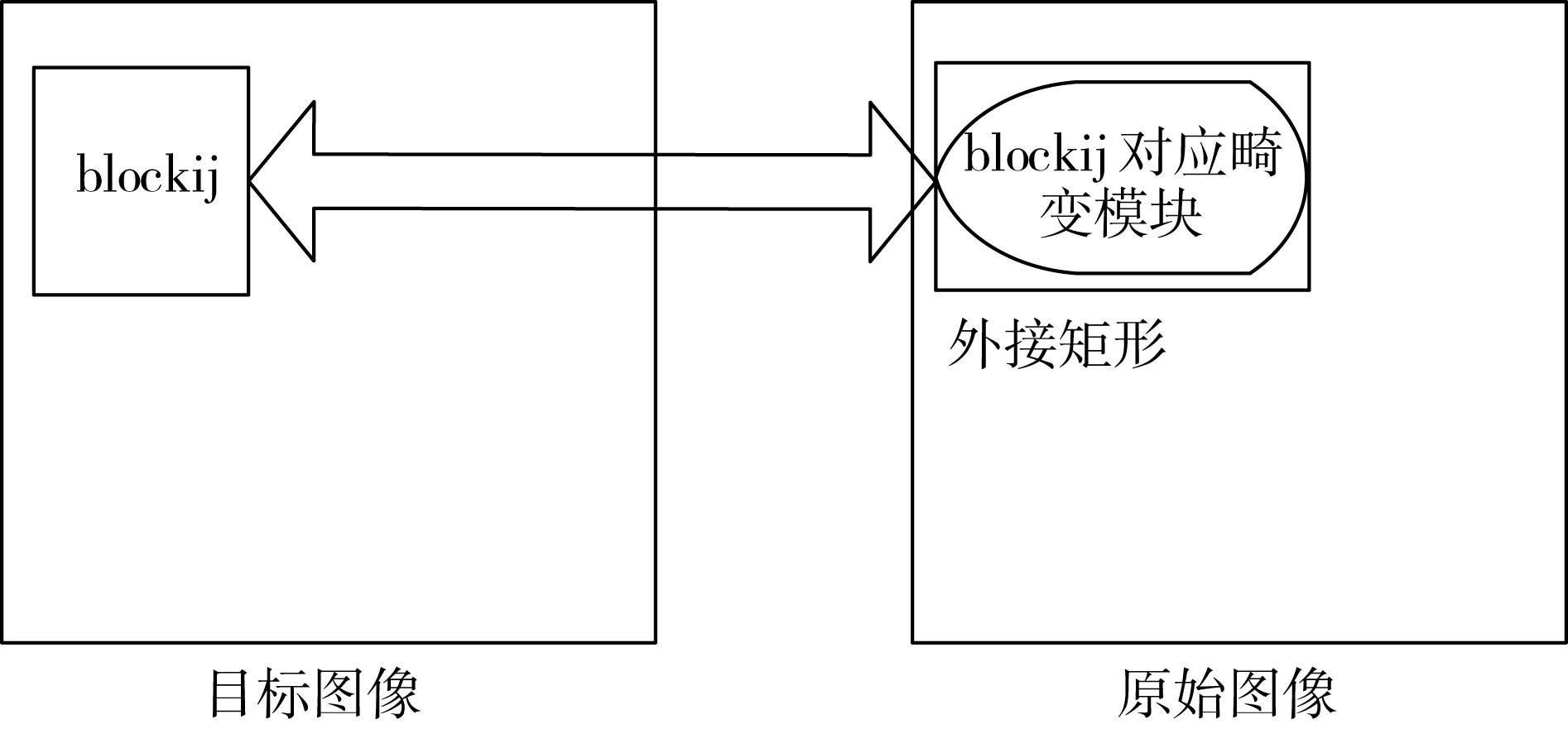
图2 原始图像到目标图像的映射过程
此方案称为阵列点阵标定板,也适用于透视变换。透视变换在FPGA的实现包括坐标生成和坐标映射,畸变矫正也包括坐标生成和坐标映射,二者的算法差异在于坐标生成实现过程不同。透视变换的坐标生成为单应性和线性,而畸变矫正的坐标生成模块中畸变模型是非线性的,其参数不同。二者的坐标映射是相同的,此部分可以融合在一起。将畸变矫正和透视变换进行合并,运行时间缩短了一半。图3所示为透视变换和畸变矫正融合流程。

图3 透视变换和畸变矫正融合流程
3 实验结果分析
在FPGA开发板ZC702平台进行矫正实验,运行环境为Win7操作系统,CPU为酷睿i7,内存为16 GiB。实验图像的分辨率是6 576×4 384,开发板的时钟频率是100 MHz。在一般软件平台下需要3 000 μs,而本方案总共耗时315 ms,速度提高了9.5倍之多。
图4所示为畸形图像矫正效果。可以看出,原始图像有明显的桶形畸变,通过矫正之后,桶形畸变明显改善。表1所示为矫正前后图像参数。

图4 畸形图像矫正效果
倾斜度是指图像有效区间外界矩形与水平方向的角度;边界最大间隙是指图片有效区和其外界矩形没有重合的最大间隙;背景亮度是指图像的平均亮度;缺陷亮度是指图像中缺陷的平均亮度。
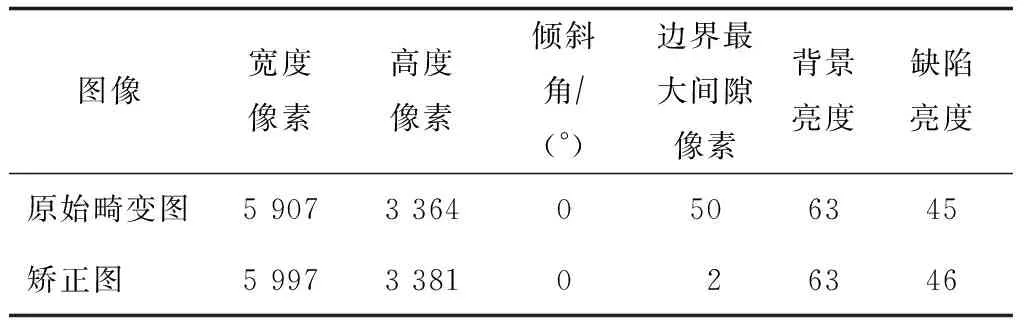
表1 矫正前后图像参数
对棋盘格图像进行校正后,图像方格的大小(宽度和高度)如图5所示。在理想状态下,校正后棋盘格图像垂直方向长度像素为485,水平方向长度像素均为670,所有方格的大小应该相同。
实验测量结果显示,方格与理想方格宽度和高度差距只在1个像素范围以内,说明矫正精度很高。

图5 矫正后的棋盘格图像
4 结 语
本次研究中,提出了阵列点阵标定板的方案,采用FPGA工具对畸变图像进行校正。实验效果图非常完美,图像矫正速度相比传统基于纯软件的方案提高了9.5倍,图像矫正的像素精度可以达到1。本次研究仅基于单通道,在以后的研究中将尝试双通道、四通道等处理技术的实验。
