高速收费站广场设计及收费亭分布优化

2018-09-10姚兴贵赵陆挺徐正阳薛良松

重庆科技学院学报（自然科学版） 2018年4期

姚兴贵赵陆挺徐正阳张超薛良松

(安徽农业大学工学院，合肥 230036)

某高速收费站广场设计存在以下不足：(1) 收费方式单一。只设计了人工收费方式，未设计半自动收费(磁卡收费)、全自动收费(不停车收费)等收费方式。(2) 未考虑出口车道容量。为了保证在入口区的吞吐量，在入口区增建了收费亭。收费亭过多，导致出口区车流量增加，而出口车道容量有限，这样很容易造成交通堵塞，从而降低收费站的吞吐量。(3) 未考虑施工成本和事故率。收费亭数量较多，一方面使收费广场的占地面积增大，建设成本上升；另一方面增加了车辆的车道合流次数，容易造成事故的发生。(4) 未考虑车辆类型的多样化发展趋势。随着科技的进步，今后将出现更多类型的自动驾驶车辆。高速收费广场必须适应这种发展趋势[1]。

在不能改变原有公路车道的条件下，如何合理设计收费站广场，保证车辆的顺利通行是亟待解决的问题。本次研究将根据高速收费站广场车辆进出口情况、行驶方式及收费方式，对收费站广场进行优化设计[2]。

1 理论与算法

1.1 排队论

排队论提供了一种对服务对象到来及服务时间进行统计研究的方法，可用于统计相关数量指标(等待时间、排队长度服务时间长短等)的变化规律。根据这些规律，可以改进服务系统的结构或重新组织被服务对象，使得服务系统既能满足服务对象的需要，又能使机构费用支出的经济性和合理性最高，或使某些指标达到最优。根据排队论，建立收费站广场模型，模型结构如图1所示。

图1 模型结构图

1.2 工程造价

工程造价主要包括2部分：一是土地购置费用；二是收费站的建设成本。土地购置费用根据收费广场的土地面积来确定，假设土地购置费用单价为c元，那么征地费用C土地为：

C土地=c[(L入口+L出口)H+0.5(H+WL)×

(H-WL)(cotθ入口+cotθ出口)+

H收费亭W收费亭B]

式中：C土地—— 收费站广场土地购置费用，元；

c—— 土地购置单价，元/m2；

L入口、L出口—— 入口区、出口区队列长度,m；

H—— 单边收费广场宽度,m；

WL—— 公路宽度,m；

θ入口、θ出口—— 扇入区、扇出区倾角,(°)；

H收费亭—— 收费亭的长度,m；

W收费亭—— 收费亭的宽度,m；

因此，建设成本C建设表示为：

C假设=c[(L入口+L出口)H+0.5(H+WL)×

(H-WL)(cotθ入口+cotθ出口)+

1.2 入口排队区长度与收费亭数的函数关系

入口区的排队长度由收费亭数所决定。收费亭越多，排队的车辆就越少，吞吐量也就越大；反之，排队车辆越多,吞吐量就越小。假设：车辆流为泊松流在某段时间内到达的车辆数是满足泊松分布X～P(λEN)，在一定时间内到达的车辆平均到达率为λEN，3种车辆的比例分别为k1、k2、k3，3个收费亭的数目分别为B1、B2、B3，3种收费方式服务率分别μ1、μ2、μ3[3]。

基于M/M/B排队模型，得出各类车辆排队数与收费亭数之间的函数关系：

ρi—— 系统的服务强度；

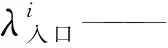
μi—— 不同收费亭的服务率；

Ni—— 到达各个收费亭车辆数量。

1.3 出口排队区长度与收费站数的函数关系

当车辆离开收费广场时，无须区分其类型。因此，在出口车道确定的情况下，扇出区内的队列长度由总交通量确定。

到达出口区域车辆的概率满足泊松分布，因此,在扇出区车辆的平均到达率是：

2.1 两组新生儿3种疾病初筛率比较研究组筛查134 886例，对照组筛查128 828例。研究组新生儿的CH、PKU和G6PD缺乏症的初筛率(97.78%)均明显高于对照组(92.05%)，差异有统计学意义(χ2=4 539.07，P<0.05)。

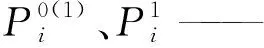
基于模型M/M/L，有：

式中：L—— 车道数；

μ—— 总服务率，辆/h；

λ出口—— 出口区车辆的平均到达率，辆/h；

ρ—— 出口系统的服务强度；

P0—— 出口系统状态概率。

1.4 事故率函数

假设收费亭与车道一一对应，显然，当车辆进入收费站对应的车道类型时，只需作直线运动即可。在此，改变车道的时间上限为B-L。单位时间和单位面积在入口扇入区和出口扇出区的合并时间上限为：

I入口=λ入口(B-L)/S入口/T入口

I出口=λ出口(B-L)/S出口/T出口

式中：I入口、I出口—— 扇入区、扇出区事故率；

T入口、T出口—— 扇入区、扇出区等候车辆时间，h；

S入口、S出口—— 扇入区、扇出区面积，m2。

在入口扇入区和出口扇出区，等候车辆在预期时间内会相遇：

式中：D入口、D出口—— 扇入区、扇出区的排队车辆数。

下面计算扇入、扇出区发生交通事故可能造成的损失：

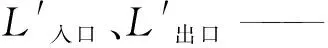
Pi—— 不同类型车道合并发生事故的概率；

Ci—— 每次事故造成的损失；

T收费站—— 收费站广场的使用寿命，a。

当车辆的平均到达率λ、车道数L、收费站数量B确定时，显然扇入区和扇出区交通事故损失只能由出入口扇形角来决定。

2 方案数据

收费站广场计算所需数据如下：到达率，600辆/h；车道宽度,3.5 m ；收费亭宽度，5.8 m；收费亭长度，4.2 m；车辆长度，5.0 m；车间距，5.0 m；道路建设成本，13 821元/m2；使用寿命，20 a。选择不同收费方式时，服务率和收费亭建造成本有所不同。选择人工收费方式时，服务率为350辆/h，收费亭建造成本为366 903元/个；选择半自动收费方式时,服务率为550辆/h,收费亭建造成本为450 462元/个；选择全自动收费方式时，服务率为1 200辆/h，收费亭建造成本为523 340元/个。

收费站广场计算结果总共有8 000种组合，在此只选择部分结果(见表1)。