基于中心节点和局部优化的复杂网络社团划分方法*

（平顶山学院计算机学院，平顶山467000）

1 引言

自然界与现实世界中的许多系统都可以用由节点和边组成的网络抽象地来表示，如社会关系网、流行病传播网、蛋白质交互网、Internet网络等，这些网络因其具有高复杂性被称为“复杂网络”。复杂网络通常具有小世界效应和无标度特性这两个统计特性。其中，“小世界效应”是指复杂网络具有短路径长度和高聚类系数的特点[1]；“无标度特性”则是指复杂网络中的结点的度服从幂率分布特征[2]。“社团结构”是复杂网络的一种重要结构特性，指的是社团中的点相互连接紧密，而这些点同社团外的点连接较为松散[3]。社团的发现和划分对于分析网络的组织结构、功能划分和成员关系等有着重要的理论意义和实际价值。

近年来，随着社团结构研究不断深入，社团挖掘算法被主要分为全局社团挖掘算法和局部社团挖掘算法。全局社团挖掘算法基于全网信息进行分析，如谱聚类算法[4]、GN 算法[5]、快速 Newman 算法[6]，但目前复杂网络的规模愈来愈大、动态性愈来愈强，导致算法的普适性、复杂度和效率等有待改进。局部社团挖掘算法基于网络的局部信息进行挖掘，如Clauset等提出的基于局部模块度R（R是社团内部总边数与社团内外边数之和的比值）的算法，它是通过最大化局部模块度增量来进行局部社团搜索[7]；Luo等提出的另一种评价局部模块度的指标M（M是社团内部总边数与社团外部节点和边界节点连边数之比）的算法[8]，其中，局部社团的规模、初始节点的位置等均会影响到社团最终的划分结果。评价社团划分算法的优劣，一个通常的做法是对每个划分给出一个度量，较合理的划分有较高的度量，优化该度量以得到最优或次优的社团结构。第一个 (也是目前最有效的)度量是“模块优度”（modularity），是由 Newman 在 2004 年提出的[9]，其值越大说明社团结构越明显，在实际网络中，该值通常位于0.3～0.7之间。

本文结合复杂网络社团结构的相关研究，提出了一种基于中心节点和局部优化的复杂网络社团划分方法。该算法首先通过多个节点中心性指标对复杂网络中节点的中心性进行综合判断，找出网络的中心节点集，接着使用局部优化思想基于每个中心节点进行社团扩张，从而形成多个社团，然后再对一些特殊节点进行处理，最终实现整个复杂网络的社团划分。

2 基于多属性判别和相似性的社团中心节点发现算法

Reihaneh等人首次提出了基于中心节点的社团定义，即将社团看作由一个领导者和聚集在其周围的跟随者组成，其中领导者就是社团的中心节点[10]。因此，在复杂网络的社团划分中，首先要做的就是寻找网络的中心节点，然后再根据中心节点选取适当的方法进行社团挖掘。

2.1 节点中心性指标

节点的中心性评价指标较多，下面仅对新算法需要用到的度中心性、介数中心性、接近中心性三项指标展开介绍。

(1)度中心性

度中心性（degree centrality，DC）是描述无标度网络结构的基本参数[11]。为了适应不同规模的网络，这里进行归一化处理，定义度中心性为节点实际关联的边数与可能关联的最大边数之比。节点v的度中心性DCv表达式为：

其中，n为网络中节点的个数，d(v)是节点v的度，指其实际所关联的边的数目。

度中心性表明了节点在网络中的直接影响力，其值越大，节点属于局部中心点(即社团中心点)的可能性越大。

(2)介数中心性

介数中心性（betweenness centrality，BC）用途经节点的任意节点对间最短路径的多少来衡量该节点在网络中的地位。节点v的介数中心性BCv表达式为：

其中，V为网络中节点的集合，gxy(v)表示节点x和y之间途经节点v的最短路径的条数，gxy为节点x和y之间最短路径的总数。

若一个节点是网络中其他节点对之间通信的必经之路，则其在网络中必有重要地位，因此，节点的BC值越大，说明在网络传输信息、物质或能量时，其负载越重，可以被认为是网络的中心节点之一[11]。

(3)接近中心性

接近中心性（closeness centrality，CC）用节点到网络中其它节点的距离来衡量该节点是否处于中心地位。节点v的接近中心性CCv表达式为：

其中，n为网络中节点的个数，d(v ,u)表示节点v到u的距离，即两节点之间最短路中边的数量。

一个节点到网络中其它节点的距离越短，节点的接近中心性的值就越大，表明节点居于网络中心位置的可能性越大。

2.2 基于多属性判别的节点中心性计算

由上述节点中心性指标的定义可以看出，不同的指标从不同的角度描述了节点在复杂网络中的中心程度。由于只利用单一中心性指标来计算节点在网络中的中心性可能存在偏差，故此提出一种基于多属性判别的节点中心性计算方法。该方法将网络中的每一个节点作为一个方案，将节点的多个中心性指标作为方案的属性，则节点的中心性计算就转化为一个多属性判别问题[12]。

设网络中有n个节点，则对应的方案集合可以表示为P={P1,P2,…,Pn}，若节点的中心性指标有m个，则对应的方案属性集合I={I1,I2,…,In},第i个节点的第j个指标的值记为Pi=(Ij)（i=1,2,…,n;j=1,2,…,m。下同），构成判别矩阵：

由于各指标的量纲不同，为了便于比较，对上述矩阵做如下标准化处理：

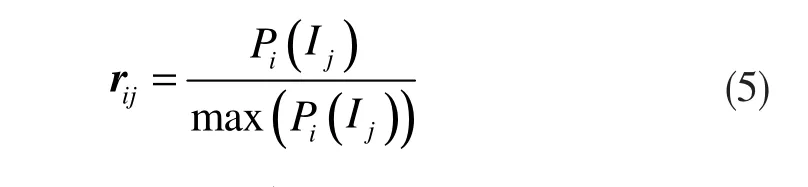
标准化处理后的矩阵记为 R=（rij）n×m。

设第j个指标的权重为ωj（j=1,2,…,m；则加权标准化判别矩阵为：

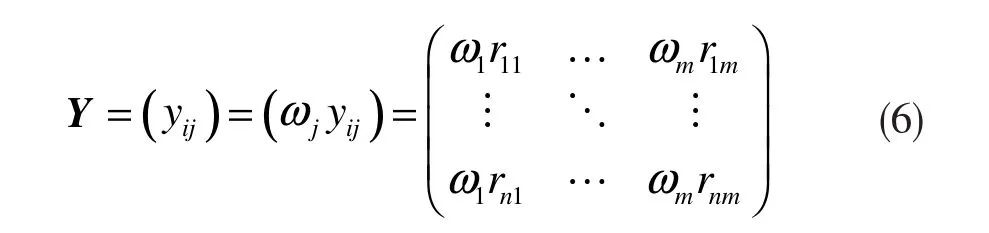
由上，计算第i个节点的综合中心性Ci为:

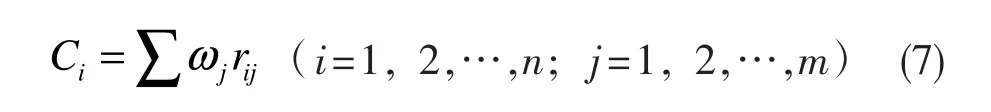
采用度中心性DC、介数中心性BC、接近中心性CC这三个指标对节点的中心性进行综合判断，各指标的权重按照文献[12]中使用的层次分析法进行计算，得到 ωDC=0.5493，ωBC=0.2616，ωCC=0.1891。

2.3 社团中心节点发现算法

基于不同社团的中心点之间应当保持一定距离的思想，还需要对节点之间的相似性进行计算，在选取综合中心性值大的节点时，将相似度极高的节点去掉。

(1)节点相似性

节点相似性用两个节点的共有邻居节点的数目来描述节点间的紧密程度，节点u和v的相似性Suv的表达式为:

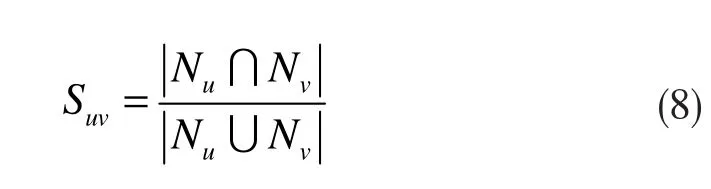
其中，Nu表示节点u的邻居节点集（且包含u点自身）表示节点u和v的共有邻居节点的数目表示节点u和v包含自身在内的所有邻居节点的数目。

一般情况下，两个节点的相似度越高，即Suv值越大，则这两个节点属于同一个社团的概率就越大。

(2)算法描述

至此，给出基于多属性判别和相似性的社团中心节点发现算法，首先根据综合中心性值选取候选中心节点，然后计算候选节点之间的相似度，相似度大的话，就将相似的两个节点中综合中心性值较小的那个节点删掉。算法流程如图1所示。

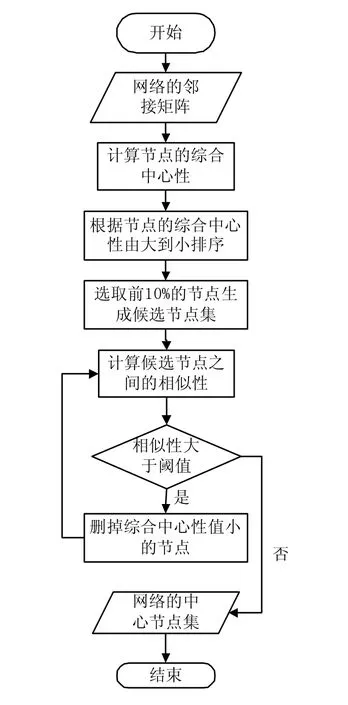
图1 复杂网络中心节点发现算法流程图

3 基于局部优化的社团划分方法

社团往往是指一个内部连接紧密、外部连接松散的子图。在确定了网络的中心节点集后，对每个中心节点利用局部优化的思想，不断地将邻近节点归入社团以实现社团规模的扩大，从而形成多个局部社团。下面先给出局部模块优度的定义，然后对基于局部优化的社团划分算法展开描述。

3.1 局部模块优度

用社团的局部模块优度LC来衡量一个社团划分的优劣，其表达式为:

其中，Ein是社团内部边的数目，内部边指边的两个顶点都在社团中；Eout是社团外部边的数目，外部边指的则是边的一个顶点在社团内部，另一个顶点在社团外部。

加入邻居节点后的社团局部模块优度LC'的表达式为：

加入邻居节点后，社团的局部模块优度增量ΔLC的表达式为：

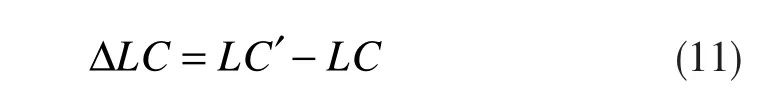
通过ΔLC可以衡量邻居节点对社团局部模块优度的影响，进而判断该邻居节点是否要划归到社团内部。

3.2 社团划分算法描述

基于局部优化的社团划分算法，是逐个计算加入邻居节点后的局部模块优度增量ΔLC，将增量大于设定阈值的邻居节点加入候选节点集，然后从候选节点集中选择与社团具有最多共同邻居节点的节点来更新社团，直到没有大于设定的增量阈值的节点出现。以一个中心节点为例挖掘以该节点为中心节点的社团，算法流程如图2所示。

在对所有的中心节点执行完局部社团挖掘后，需要对一些特殊节点进行处理。一类是未被划分至任何社团的节点，另一类是被划分至多个社团的节点，这些节点最终均将被划分至与其有最多邻居节点的社团。

4 实验验证

4.1 算法结果评价指标

主要的算法结果评价指标包括以下三种：

(1)准确率（Precision，P）

准确率为划分结果中正确节点数量与划分结果中总节点数量之比，表达式为：

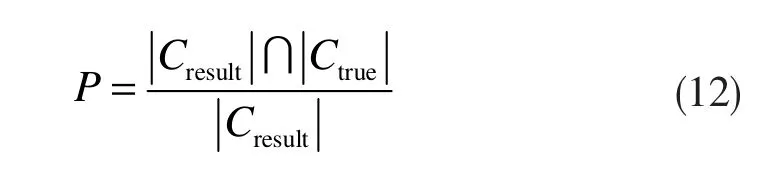
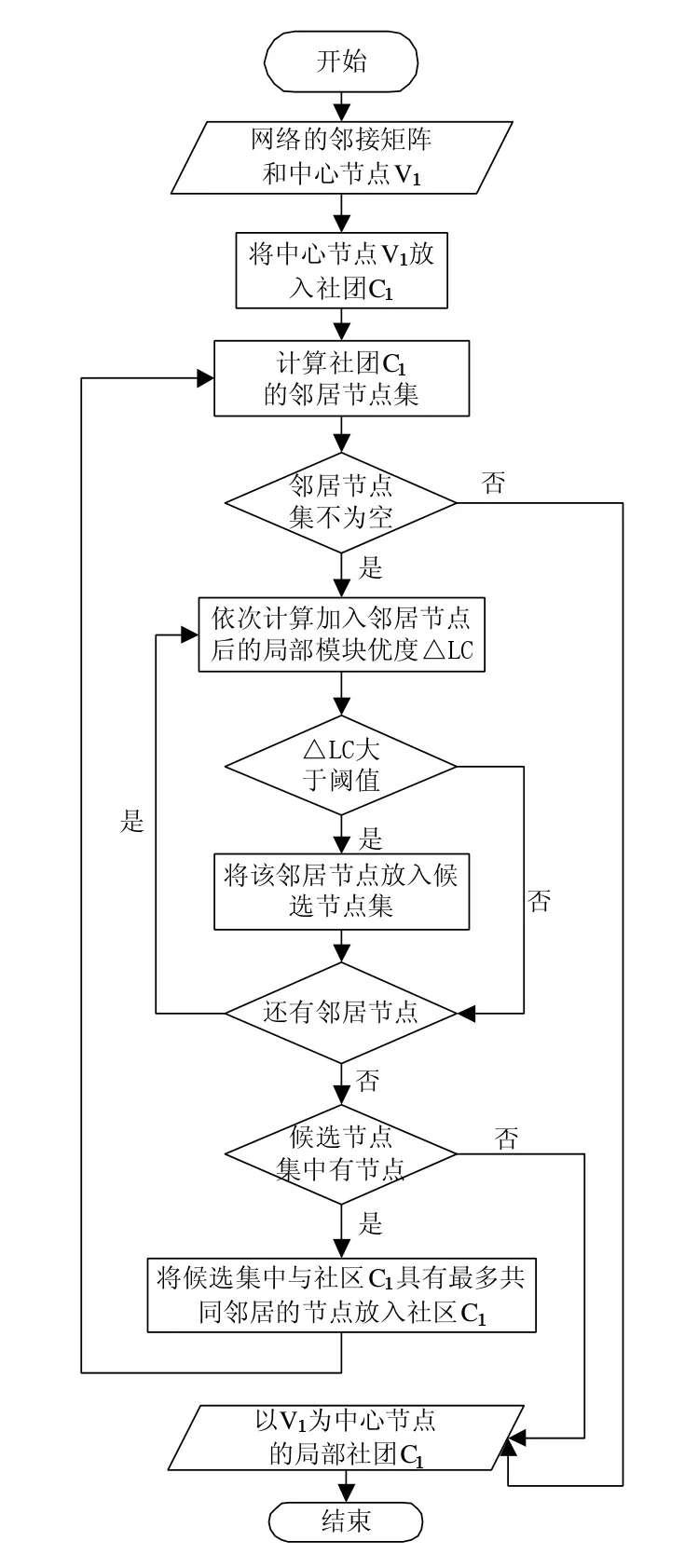
图2 社团划分算法流程图

(2)召回率（Recall，R）

召回率为划分结果中正确节点数量与真实社团中总节点数量之比，表达式为:

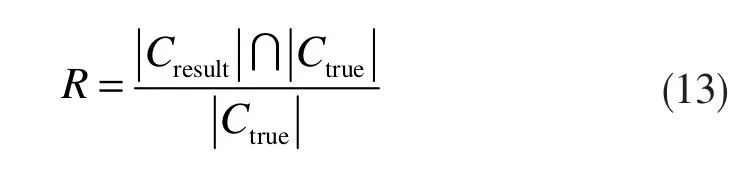
(3)综合评价指标

为防止过分割和欠分割的情况，用综合评价指标F来对社团划分进行总体评价，表达式为:

4.2 实验结果

为了验证算法的准确性，分别以空手道俱乐部成员关系网络数据集Zachary[13]和海豚网络数据集Dolphin[14]为例进行了测试。经验证，中心节点相似度阈值和局部模块优度增量阈值分别为0.3和0.33时，最符合真实的网络社团结构。

算法对Zachary的测试结果如图3所示，其中，网络被分成了两个社团。

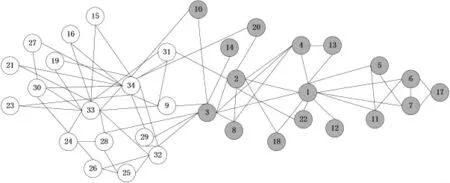
图3 Zachary社团结构图

实验中，针对上述定义的准确率、召回率、综合评价这三个算法评价指标，将此算法与引言中介绍的R算法及M算法进行了对比。对比结果如表1所示，从中可以看出，在Zachary数据集的测试结果中，此算法明显优于其它算法，在Dolphin数据集的测试结果中，除了准确率低于R算法，其它指标均优于所对比的算法。

表1 算法对比数据表

5 结束语

对复杂网络中节点的度中心性、介数中心性、接近中心性、相似度、局部模块优度等指标做了归纳、整理并适当加以扩展。分别应用基于多属性判别和相似性的社团中心节点发现算法和基于局部优化的社团划分方法对Zachary和Dolphin数据集进行了测试，同时与R算法和M算法进行了对比，结果表明新算法具有较好的社团划分能力，可以有效地挖掘出社团结构。在此基础上，进一步降低算法的时间复杂度和解决大规模真实网络应用中的优化问题，将是下一步的研究重点。