不良交通流状态实时监测支持向量机模型算法研究

游锦明，方守恩，唐 棠，张兰芳

(同济大学道路与交通工程教育部重点实验室，上海201804)

0 引言

随着我国高速公路网络的不断完善和加密，高速公路对国民经济增长和社会发展方面起到了巨大的推动和促进作用.截止2015年底，我国公路总里程达到457.73万km，其中高速公路12.35万km，交通通达性的提高也大大地促进了高速公路出行需求，同时其事故数量也一直居于高位.由于高速公路封闭的特性，车辆在高速公路中行驶时车速较高，发生事故程度更加严重，救援时间也较长，事故所造成的损失也更大.据公安部2015年道路交通事故统计年报[1]统计，2015年，高速公路交通事故起数8 252起(占总数4.39%)，死亡人数5 477(占总数 9.44%)，受伤人数 11 515(占总数 5.76%)，直接财产损失348 251 010元(占总数33.59%)，相对于一般公路而言，高速公路事故致死致伤率较高，高速公路安全形势十分严峻.因此，各级交通安全管理部门和公众开始聚焦高速公路安全出行，着力打造信息化下的平安高速公路，这也为信息化发展下的高速公路交通运行安全风险监测预警研究带来了契机.

国内外针对高速公路交通运行安全风险监测预警方面开展了大量的研究.国外由于高速公路建设起步时间较早，高速公路信息化程度较高，因此，国外高速公路上的交通流检测设备布设密度较高，种类较为齐全，国外大量的专家学者通过充分利用该部分连续的交通流检测设备所采集的海量交通流数据，开展了大量的不良交通流状态识别与事故先兆方面的研究，旨在通过对不良交通流的分辨，从而达到实时事故风险预测的目的.Hassan等采用随机森林和配对案例对照的Logistic回归方法对低能见度下的事故风险进行研究，结合气象站检测的气象数据，最终模型能够达到69%的事故预测精度[2].Shi等通过对未处理的自动车辆识别系统原始数据对事故风险进行研究，采用多层随机参数模型和负二项模型进行建模来提升模型对于复杂数据和样本间的非匀质性的适应能力，研究表明低速、高速度离散性和高流量会显著提升事故风险[3].Kwak等针对不同路段(基本路段，匝道邻近区域、匝道)不同交通状态(拥堵、非拥堵)分别构建了Logistic回归模型、遗传算法模型和综合模型，结果发现综合模型的AUC值高于单一模型(高约7%～11.2%)，说明综合模型的分类预测效果较优[4].

国内研究受限于交通流数据稀缺，对不良交通流检测预警的研究较少.孙剑等基于上海市快速路上的线圈交通流数据和事故数据，采用贝叶斯网络(BN)对事故风险进行建模，分别对事故点前后2组检测器和4个时间段的8组交通流数据进行建模，结果表明使用事故点上下游各一检测器、基于事故前5～10 min内的交通流数据的模型效果最优，其事故预测精度达到了76.94%[5].总体而言，由于国内外的驾驶习惯、交通模式上的差异，国外该部分研究成果无法在国内高速上得到验证和应用；而少量基于城市快速路的事故预测模型同样是基于密集检测器数据建立的，无法在检测器稀缺的高速公路上得到验证与应用，因此，本文将基于我国高速公路实际交通流数据现状，对不良交通流状态实时监测进行研究.本文主要由以下部分组成：①数据来源与准备，主要介绍了数据来源和基本的数据筛选过程；②基于主成分分析法的不良交通流状态评价参数框架构建，主要介绍了主成分分析法的分析过程和车道级的交通流参数提取过程；③基于自适应过抽样方法的不良交通流状态监测支持向量机模型，主要介绍了自适应过抽样方法、支持向量机建模过程.本文的主要技术路线如图1所示.

图1 技术路线图Fig.1 Modeling process in this study

1 数据来源与准备

数据来源于G60沪昆高速公路上海段，路段总长48 km，双向3～5车道，设计速度120 km/h.

1.1 事故数据

数据分为2个部分，事故数据和交通流数据.研究采用的原始事故数据为2014年1月1日～2015年9月30日期间，沪昆高速(G60)上海段发生的所有事故.研究期间内总共发生有记录的事故913起.由于本文研究对象为不良交通流状态监测判别，所以仅考虑与不良交通流状态密切相关的车辆间事故作为研究对象，而与不良交通流状态关系不甚密切的由车辆因素导致的车辆故障、货物洒落、货物着火等因素导致的单车事故则不考虑在内，故最后仅将追尾、刮擦事故纳入分析范畴，共547起.

1.2 交通流数据

交通流数据方面，沪昆高速(G60)上海段沿线共布设了9组车流检测器，负责采集9个断面的流量信息.检测器布设信息在表1中列出.其中由于编号D05～09的车流检测器布设在匝道上，桩号及布设条件不明，所以仅考虑4个高速公路主线线圈检测器检测的数据用以后续分析.

表1 车流检测器布设信息Table 1 Installation information of the loop detectors

1.3 样本构建

本文旨在研究不良交通流状态的监测，因此将车辆间事故作为不良交通流状态的演化结果进行分析，同时考虑到G60沪昆高速上布设检测器的密度问题，由于主线上检测器布设密度过低，两检测器间最短的距离为2.63 km，最远的为18.6 km，检测器间平均距离8.7 km，与国外研究中采用的平均0.5 mile(约800 m)的检测器密度相比过于稀疏.此外，由于检测器布设间距差异性过大，上下游检测器数据之间的相关程度不一，故采用单断面检测器的数据作为衡量路段交通流状态的基础依据，那么本文的因果逻辑关系便为通过对单断面检测器的交通流状态的演化判别实现对车辆间事故的预测.

为了有效地对不良交通流状态进行分辨，采用流行病学中常用的案例配对对照方法进行样本选取，即需要对有效事故样本所对应的不良的交通流状态提取相应的几组正常状态交通流状态数据作为对照组.为了排除工作日、时间段等因素的影响，本研究提取每一组有效事故发生前2周、前1周、后1周、后2周的同一工作日的同一时段的检测器数据作为对照.提取的每一组数据应该添加上对应的事故编号，便于建模时对不同条件下的事故样本及该样本的对照组进行筛选.

由于原始数据部分时段检测器的数据缺失或检测器线圈返回故障状态信息，会导致数据库查询返回的数据为空或无效的状况.对于出现数据异常的事故应加以排除.同样对照组检测器数据查询也会存在数据缺失、返回空值和数据无效的情况，需要对该类对照组进行排除.在时间片段选取和集计方法上，考虑到最终分辨效果和实际应用中的实时监测目的，选取有效车辆间事故前10 min至事故前5 min内的5 min的交通流数据作为衡量不良交通流状态的标准，并同步将20 s的原始线圈采集的交通流状态数据集计为5 min的交通流状态数据，减少数据噪声的影响.

1.4 车道级参数选取

在参数选取方面，为了充分利用车道级交通流数据的特点，引入平均值、标准差、变异系数和车道间相关系数4种计算方法.在数据类型上采用了检测器返回的流量、速度、密度3类数据.研究路段为单向3～5车道，所以采用了L(left)、M(middle)、R(right)和A(all)这4个值来标记不同的车道.特别要指明的是，对于单向4车道的道路，M可代表中间的2个车道；对于单向5车道的道路，M可代表中间3个车道.通过对上述3个维度的组合，最终构建出1个含45个参数的交通流参数体系，其中平均值、标准差、变异系数各12个，车道间相关系数9个，即对以下3个15行3列(t为时间片段编号，其中Q2t、V2t、C2t分别指中间若干车道的流量、速度、占有率在第t个20 s时刻所采集的交通流信息)的矩阵(流量矩阵、速度矩阵、占有率矩阵)提取相应的特征信息.

由于我国实行法定节假日高速通行免费的政策，节假日期间高速公路的流量与平常会有明显的差异.G60作为上海与杭州的主要交通干道，其交通流也会受到明显的影响.在建模工作中，需要将节假日作为1个重要的控制条件.对数据进行以上多次筛选后，排除节假日期间发生的事故，最终得到116起有效事故数据组参数与401组对照组数据组参数.部分参数相关统计信息如表2所示.

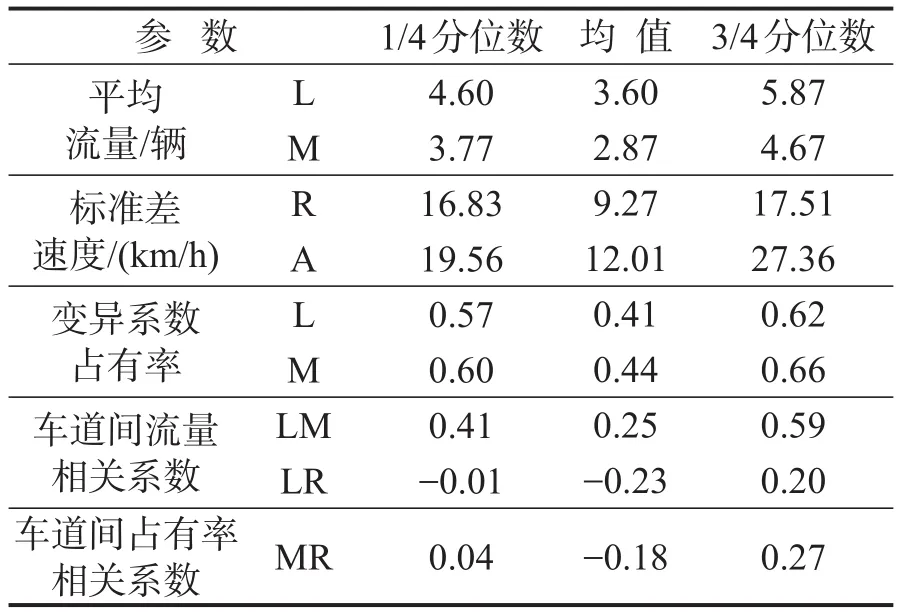
表2 部分车道级参数统计信息Table 2 Summary statistics of part of the lane-level parameters

在初步的样本参数确定后，下面将对不良交通流状态评价参数框架进行优化构建.

2 基于主成分分析法的不良交通流状态评价参数框架构建

主成分分析(Principal Component Analysis，PCA)是研究如何将多指标问题转化为较少的综合指标的一种重要统计方法，能将高维空间的问题转化到低维空间去处理，使问题变得比较简单、直观，而且这些较少的综合指标之间互不相关，又能提供原有指标的绝大部分信息.在实际研究工作中，通常只挑选前几个方差最大的主成分，从而达到简化系统结构、抓住问题实质的目的.

本文选用SPSS中的因子分析模块进行主成分分析工作，按照初始特征值的抽取指标为1的规则，最终从45个成份中提取了前9个成份作为新的变量，这9个成份对于原有变量的解释程度为84.185%(即方差的累积值).在主成分分析中，由于因子的舍去不可避免地会导致部分信息的丢失，通常的分析经验认为新的因子对旧变量保留有85%的解释度即可.提取的前9个变量的解释度为84.185%，基本满足要求，所以将初始特征值的抽取指标设置为1是比较合理的，其对应过程的碎石图如图2所示.

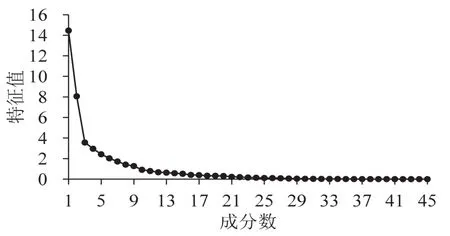
图2 主成分分析结果碎石图Fig.2 Scree plot of the principle component analysis

对该9个变量的主要成分计算其因子负荷、特征向量，经过标准化后最终得到新的9个变量对应的值，用以在后续建模工作中作为预测模型的训练数据，表3为主成分分析后新样本变量的参数统计信息.

表3 主成分分析后样本参数统计信息Table 3 Summary statistics of variables afterprinciple component analysis

3 基于自适应过抽样方法的不良交通流状态监测支持向量机模型

本文对不良交通流状态的判别基于事故发生与否，为典型的模式识别中的分类问题.而支持向量机在模式识别各种算法中，由于具备较强的泛化能力，能够较好地解决传统学习方法中高维数据、小样本、非线性和局部极值等问题，能够较好地对样本进行分类识别.因此，本文选用常用的基于RBF(径向基核函数)的支持向量机分类器CSVC模型作为识别分类模型，其决策函数为

式中：xi，yi，αi，b为模型优化求解得到的参数；K(xi,x)为高维映射选用的核函数.

由于样本中不良交通流状态对应的样本较少，约占总数的20%，机器学习算法在遇到该类样本时，易导致样本不均衡识别现象，即分类明显偏重于多数类样本，因此，为了避免样本不均衡给建模带来的影响，采用自适应过抽样方法对样本结构进行优化，从而避免样本不均衡问题.

在C-SVC模型的构建时，引入了常数C作为惩罚系数控制损失的大小.模型求解中C可作为调节参数，影响训练模型的分类性能.此外，RBF核函数中γ参数也是模型训练前需输入的常数，该参数的数值也会明显影响模型的分类性能.所以应用SVM方法解决分类问题还需解决SVM模型参数及核函数参数的寻优问题，得到分类效果最佳的1组C、γ参数.对ADASYN算法处理后得到的样本按测试集与训练集比例3∶7的比例进行多次随机分配.对上述随机分配情况下的样本采用网格遍历法进行参数寻优，得到的C最优值范围为[0.03，1.74]，γ最优值多为0.57.根据多次试验总结，设C=1，γ=0.6，对该组参数进行多次样本随机分配建模，建模的结果如表4所示.

表4 测试集分类结果Table 4 Classier performance of the test dataset(%)

采用测试集分类准确率对C-SVC模型性能进行评价必选可以发现，C=1，γ=0.6的参数组合能保证多次试验下分类准确率维持在较高的水平，该参数组合的取值是比较合理的.在9次试验中获得了9个C-SVC分类模型，其分类效果各有差异，对比各模型分类准确率，选择分类效果最好的第9次试验模型为最终的不良交通流状态实时判别监测模型，其事故对应的不良交通流状态分类准确率高达79.55%，表5为国外相似研究中相关方法和结果.

表5 模型性能对比Table 5 Comparison of the performance of the models

同国外既有研究中构建的模型比较可以发现，本文提出的基于单检测器的实时监测算法能够有效地识别不良交通流状态，从而为交通管理人员提供可靠的决策支持.

4 结论

本文结合国内高速公路稀疏检测器现状，提出了基于单检测器的不良交通流状态实时监测判别支持向量机方法.采用事故所对应的交通流状态作为不良交通流状态进行研究，通过对海量车道级的线圈检测器采集的交通流数据提取平均值、标准差、变异系数、车道间参数相关系数等45个参数指标，经由主成分分析法对参数进行优化实现参数降维最终保留9个参数，最后结合自适应过抽样方法避免样本不均衡现象，采用C-SVC支持向量机模型实现了对不良交通流状态的实时监测识别，其识别精度高达79.55%，可以有效地对不良交通流状态进行识别.