面向班型动态生成的地服人员排班算法

卢 敏，王 莉

(1.中国民航大学a.中国民航信息技术科研基地，b.计算机科学与技术学院，天津300300；2.中山大学机器智能与先进计算教育部重点实验室，广州510275)

0 引言

为了快速且有效地保障航班地面服务，大型机场地面服务部门需生成员工排班方案，将员工分配到班型(组)中，以班型为航班的保障单元，其原由是：①班型有利于地服部门以组为单位监控服务质量和计算员工工作时长；②班型落实了低资质员工需要高资质员工从旁指导和协助的硬性要求；③班型能满足员工自愿组对的个性化需求.

由于机场地服无法获知班型数，机场地服人员排班本质是融合班型动态生成、员工层次资质和员工白夜班等约束的人员排班问题.人员排班是指通过最大化任务完成率和员工满意度将员工分配到任务上[1]，被应用于交通[2]、医疗[3]、酒店[4]等领域.班型动态生成是指自动生成班型，在此基础上将员工和航班分配到班型中，且要求班型内员工能够满足组内航班的资质需求.资质是指员工执行任务的能力，而层次资质是指员工教育程度和工作经验使得员工资质存在层次关系[4].员工白夜班指员工每天只能从事白天或夜晚的航班.由于班型内的人员分配、班型内航班分配都是建立在已知班型数的重要前提下，而实际应用中班型数是未知而需要动态生成，使得机场地服排班是一个具有挑战性的问题.

直观上可借助面向层次资质的排班算法[5-7]和面向班型的排班算法[8-9]解决机场地服人员排班.然而，面向层次资质的排班算法[5-7]未考虑班型约束，而面向班型的排班算法[8-9]则是在已知班型数前提下优化班型内的人员构成和任务集，不适用班型数未知的排班问题.此外，它们采用的列生成技术、启发式算法和贪婪算法不适用班型动态生成约束.

为解决上述问题，提出面向班型动态生成的地服人员排班算法.算法首先生成满足员工层次资质和白夜班的可行解，在此基础上将优化问题分解为班型内人员构成、班型内航班集、优化班型等3个子问题，通过block Gibbs有放回抽样快速优化上述子问题.

本文主要贡献为：①提出了面向班型动态生成的地服人员排班算法，解决了大型枢纽机场地服人员排班问题，可拓展应用于机组人员排班和医生/护士值班等；②针对班型未知的排班问题，提出基于block Gibbs替换抽样求解算法，通过迭代合并、分裂、重组合班型以更新班型，并在此基础之上重新调整班型内的人员构成和任务构成.

1 问题定义与建模

1.1 问题定义

机场人员排班是在给定航班计划和员工资质集前提下，生成以组为单位的排班方案.同一组内航班需满足的规则为：

(1)同一组内航班必须为归属同一天；

(2)同一组内航班白夜班类型须一致；

(3)满足组内航班的层次资质数.

S={1,2,…,|S|}表示航班地面保障的任务种类，|S|表示总任务类型数；L={1,2,…,|L|}表示航班保障涉及的员工资质种类.

假设员工集合P={1 ,2,…,d}.每名员工i具备资质集合SKi∈{0,1}|S|×|L|，其值为 1 表示员工i在任务类型s上具备l类型资质.员工工作经验不同使得员工在同一种任务类型上具有向下兼容的层次资质，即当

优化变量xijg∈{0,1}表示员工i是否服务第j天第g个班型，取值为1代表执行.据xijg生成1周班型集合Φ={(djg,bjg,ejg,Rjg,Pjg,Χjg)|j=1,…,7;g=1,…,nj} ，分别表示第j天第g个班型的白夜班类型、开始时间、结束时间、资质需求数、员工集合和航班集合，其中班型开始(或结束)服务时间为班型内所有航班中最早开始(或最晚结束)服务时间.

1.2 数学建模

基于上述建模，面向班型动态生成的地服人员排班优化目标为

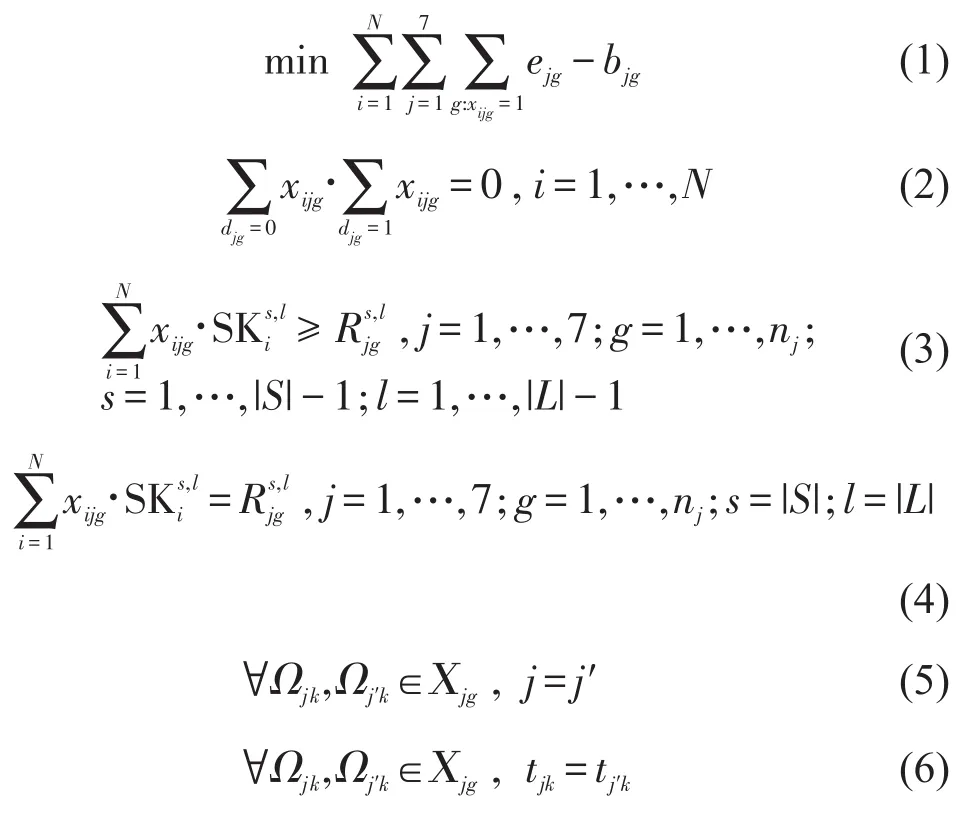
式(1)旨在最小化员工总工作时长，其中员工i第j天的工作时长等于员工i在第j天保障所有航班的时长总和.式(2)表示员工只能选择服务白天或夜晚的班型.式(3)和式(4)表示每个班型内任务所需的资质数需得到满足，式(3)融入员工资质层次结构，即高资质员工可弥补需要低资质员工的空缺；式(4)表示为班型分配的总人数恰好等于班型所需的总人数.式(5)表示同一个班型内所有航班来自同一天.式(6)表示同一个班型内所有航班的白夜班类型一致.

2 求解算法

提出基于block Gibbs的快速求解算法以优化式(1)～式(6)，如Algorithm 1所示.其核心思想是：首先设计一子模块生成满足员工层次资质和白夜班的可行解，然后设计另一子模块迭代优化班型内人员构成、优化班型内航班集、优化班型，最终生成以班型为单位的排班方案.

Algorithm 1:面向班型动态生成的地服人员排班算法输入：航班集合Ω；员工集合P；迭代次数niter；退火温度T；衰减因子β输出：员工任务排班方案{xijg}初始化：生成初始解foriter=1,…,niter：fori=1,…,N：xijg=0,j=1,…,7;g=1,…,nj采用式(9)抽取yi∼p(∙|y-i,x-i)foreachΦjg∈Φ：if(RQjg-SKi＜RQjganddig=yi)thenxijg=1 if(式(7)的值等于∑mj)then break//生成初始解迭代优化：优化班型、优化班型内人员构成和航班集foriter=1,…,niter：子问题I：优化班型内人员构成fori=1,…,N：xijg=0,j=1,…,7;g=1,…,nj采用式(9)抽样yi∼p(∙|y-i,x-i)forΦjg∈Φ：if(式(3)和式(4)不满足)thenxijg=1,yi=djg elseif(djg=yiandRQjg-SKi＜RQjg)then将班型Φjg加入到候选班型集合Φ1中foreachΦhr∈Φ1：xihr=1,Γ ={i|xihr=1,i=1,…,N}采用式(10)抽样i1∼p(i1∈Γ|x,y)令xi1hr=0子问题II：优化班型内航班集foreachΩjk∈Ω：从航班Ωjk所在班型Φjg1中移除航班Ωjk，修改班型Φjg1的开始和结束时间foreachΦj'g∈Φ：if(j'!=jor式(3)和式(4)不满足)then continue将班型Φj'g加入到候选班型集合Κ中根据式(11)抽样Φhr∼p(Φhr∈Κ|Φ)将航班Ωjk加入到班型Φhr中，修改班型Φhr开始和结束时间子问题III：优化班型foreachΦjg∈Φ：//班型合并foreachΦj'g'∈Φ：if(j'!=jordj'g'!=djg)then continue将班型Φj'g'加入到班型集合Κc中根据式(11)抽样Φhr∼p(Φhr∈Κc|Φ)，将服务班型Φjg的员工集和航班集全部加入到班型Φhr中，修改班型Φhr的开始和结束时间foreachΦjg∈Φ：//班型拆分foreachΩjk∈ Χjg：以航班Ωjk的开始时间为分界线将班型Φjg中航班分为2组航班将2个班型加入到班型对集合Θjt中根据式(11)抽样Θkjt∼p(Θkjt∈Θjt|Φ)，将班型Φjg中航班拆分为Θkjt中包含的2个班型，修改2个班型的开始和结束时间，原始班型中员工分别服务拆分后的2个班型T=T⋅β

2.1 初始可行解生成

为了快速生成满足员工资质和员工白夜班约束的初始可行解，设计了优化目标和约束，即

式(7)为优化目标，统计满足资质需求的航班数.若每个航班的资质需求都得到满足，则式(7)目标值等于总航班数∑mj；否则存在未满足资质需求的航班，无法得到初始解.式(8)为约束条件，表示员工只能选择白天或夜晚航班.

初始解生成核心是确定员工的白夜班类型和保障航班分配所需资质数.引入Xi表示员工i的任务集，yi表示员工i的白夜班类型，yi抽样分布如式(9)所示.I[A]为指示函数，当条件A成立时取值为1，否则为0.ε=le-06为平滑项.式(9)表示当存在不满足约束式(3)的班型时，将yi设置为此班型对应的白夜班类型，否则根据白天夜晚班型数量进行抽样.

2.2 迭代优化求解

优化班型内人员构成的核心是通过对同一班型内员工有放回的抽样，即先增加1名员工后抽样撤销1名员工，实现班型内人员调整以缩短员工总工作时长.具体过程为：首先确定员工白夜班类型，即撤销员工所保障的班型，判断是否存在不满足资质需求的班型，若有则将员工白夜班类型设置为不满足资质需求班型的白夜班类型，反之通过式(9)抽样确定员工白夜班类型.然后，调整员工i的保障候选班型集合Φ1中每一个班型Φhr，即xihr=1.保障班型Φhr的员工集合为Γ={i|xihr=1,i=1,…,N}，此时员工集合Γ比需求多1名员工，根据式(10)抽样1名员工i1，从该班型中撤销员工i1，即xi1hr=0.此过程保证不违反约束式(3)和式(4).

优化班型内航班集的核心是优化航班的所属班型，本质是将航班从当前班型调整到另一个班型中.首先针对航班Ωjk从原始所属班型中撤销，修改原始班型的开始和结束时间，然后构造航班Ωjk可放入的班型集合Κ，在班型集合Κ中通过式(11)抽样得到1个班型Φhr，最后将航班Ωjk放入班型Φhr中，修改此班型的开始和结束时间.其中班型集合Κ中的每一个班型需要满足：①白夜班类型须与航班Ωjk一致；②与航班Ωjk在同一天；③班型所包含的员工能够满足航班Ωjk的资质需求.

优化班型的核心是结合员工工作时长，通过分裂和合并现有班型以更新班型.

班型合并的核心是将2个班型合并为1个班型.针对班型Φjg∈Φ，将与班型Φjg同一天且白夜班类型相同的班型加入班型集合Κc中，通过式(11)在班型集合Κc中进行抽样，得到班型Φhr，将班型Φjg与班型Φhr包含航班和员工合并，修改合并后班型的开始与结束时间.

班型拆分的核心是将1个班型拆分成2个班型.针对班型Φjg∈Φ，以班型Φjg中航班的开始时间为准将班型内航班分成2组，构成班型对集合Θjg，根据式(11)在班型对集合中抽样得到1个班型对Θkjg，将原始班型Φjg中的员工分别分配到被拆开的2个班型中.

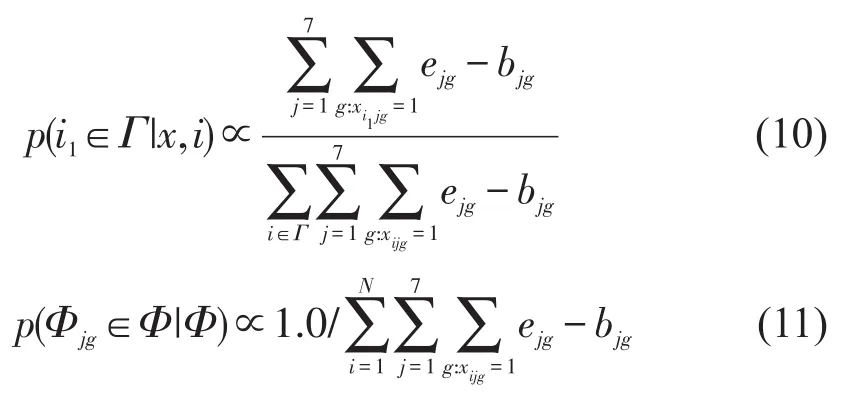
3 实验及分析

3.1 实验数据

实验数据集是某机场1周航班计划和值机员工的资质集.每个航空公司的所有航班归属于同一任务，涉及的3种资质，分别为“组长”“控制人员”“普通员工”.为描述方便，采用3表示组长，2表示控制人员，1表示普通员工，0表示没有服务资质.

航班数据包括49个航班，属性包括星期、航班号、任务类型、开始时间、结束时间、所需组长人数、所需控制人员数、所需普通员工人数，数据样本如表1所示.员工资质集则是39名员工在各航空公司(任务)的资质信息，数据样本如表2所示.

表2 员工信息数据示例Table 2 Samples from persons with skills

3.2 实验结果

算法需要人工预先设置3个参数，分别为迭代次数niter、退火温度T、衰减系数β.实验过程中T和β设置参考经验值，分别为T=100，β=0.99，niter=200,300,400.本次实验中niter设置为200，在第3.3节算法收敛性中验证niter取值200的合理性.

实验结果部分数据，如表3所示.表3中1行是1个班型，包含班型的开始时间、结束时间、班型内的航班列表和班型内的员工名单.例如，星期一第1个班型包括2个航班“PK852”“J2067”，而根据表1航班PK852共需6名员工，航班J2067需1名员工，据表2员工“王岩”同时具备“PK”“J2”类型航班资质，即能够满足班型对资质需求.

以员工“李仁骥”为例展示1周的服务班型，如表4所示，其中“21:30-02:30”指当天晚上的21:30到第2天02:30.员工“李仁骥”1周的班型都是夜晚班型，满足员工白夜班约束.此外，员工“李仁骥”在星期一和星期三都同时服务2个班型，究其原因是算法为了最小化员工总工作时长，会将员工分配到2个相邻的班型中.例如星期一的2个班型之间的间隔只有20 min.

表3 实验结果数据示例Table 3 Samples from experimental results

表4 员工“李仁骥”的1周任务示例Table 4 Tasks for Renji Li at one week

3.3 实验分析

3.3.1 班型分析

算法主要是最小化员工工作时长以生成班型，为此从两方面对班型进行分析：

(1)1周中每天航班个数与班型个数如表5所示.表5结果表明：平均每天将员工分为4组，而每组平均服务7个航班.如将班型分成白天班型和夜晚班型的情况下，则每天平均会有2个白班班型和2个夜晚班型，对管理人员更方便管控员工的上下班时间.

(2)每个班型的时长如图1所示.班型时长大多分布在[3,4)h和[4,5)h，对于机场值机人员每个班型时长[3,5)h较为合理.

表5 航班个数和班型个数Table 5 The number of flights and shifts

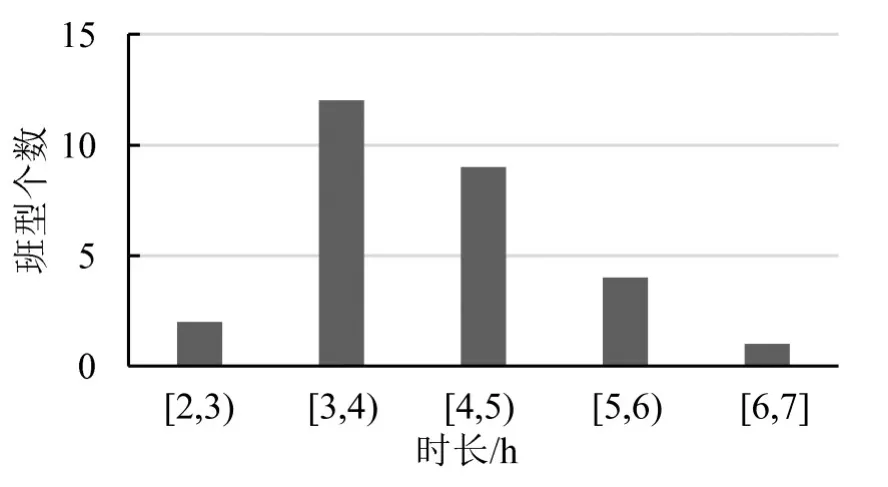
图1 班型时长分布Fig.1 Groups duration distribution

3.3.2 算法特性分析

分析算法收敛性，即随着迭代次数增加，目标函数取值的变化程度，如图2所示.算法在前50轮迭代中总工作时间迅速减少，之后趋于稳定，验证迭代次数取值200是合理的.

图2 算法收敛性分析图Fig.2 Algorithm convergence analysis

分析算法稳定性，即多次运行算法，比较员工总工作时长和算法运行时长，如图3所示.从图3可知，随着算法运行次数的增加，工作时长、运行时间趋于稳定状态.

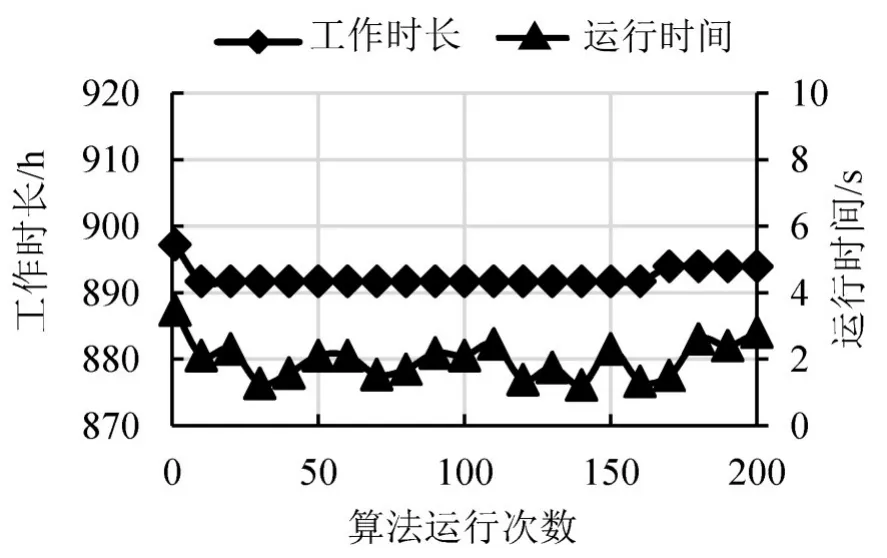
图3 算法稳定性分析图Fig.3 Algorithm stability analysis

4 结论

针对机场地服人员排班过程中班型数未知和员工层次资质等约束，提出了面向班型动态生成的地服人员排班算法.算法首先把每个航班作为1个班型，利用一子模块生成满足得到满足员工层次资质和员工白夜班的可行解.在此基础上，设计了基于block Gibbs有放回抽样算法，以迭代优化班型内人员构成、班型内航班集和班型动态生成.在国内某大型机场地服人员排班数据集上实验结果表明算法的可行性与稳定性.未来可进一步开展具有组内约束的人员排班，如班型内航班冲突和人员冲突等.