茧丝纤度曲线函数模型的构建与分析
2018-09-10黄继伟陈玄墨钱爱芬宁晚娥林海涛凌新龙岳新霞
黄继伟 陈玄墨 钱爱芬 宁晚娥 林海涛 凌新龙 岳新霞


摘要: 构建合理的茧丝纤度曲线描述模型是开展蚕品种选育、缫丝工艺制定和计算机模拟缫丝的重要基础。文章在分析了茧丝纤度曲线形态特征的基础上,将茧丝纤度曲线呈“细-粗-细,最末处最细”的特征归咎于蚕吐丝时吐丝口逐渐张开和绢丝液或吐丝力持续减弱的综合结果,提出采用Logistic函数和二次函数的复合函数来模拟茧丝纤度曲线。经非线性回归分析和模拟生成验证,确认该复合函数模型具有良好的适用性,有望成为新的茧丝纤度曲线描述和模拟生成方案。
关键词: 茧丝纤度曲线;计算机模拟缫丝;Logistic函数;二次函数;非线性回归分析 中图分类号: TS141.91
文献标志码: A 文章编号: 1001-7003(2018)11-0031-10 引用页码: 111106
Construction and analysis of cocoon filament size curve function model
HUANG Jiwei 1,2 , CHEN Xuanmo 1, QIAN Aifen 3, NING Wane 1, LIN Haitao 1, LING Xinlong 1, YUE Xinxia 1
(1. College of Biological and Chemical Engineering, Guangxi University of Science and Technology, Liuzhou 545006, China;
2. College of Textile and Clothing Engineering, Soochow University, Suzhou 215123, China;
3.Shaoxing Customs (Shaoxing Entry-Exit Inspection and Quarantine Bureau), Shaoxing 312000, China)
Abstract: The rational description model of cocoon filament size curves is an important foundation for silkworm varieties breeding, silk reeling process and computer simulation of silk reeling. Based on the analysis of morphological characteristics of cocoon filament size curves, the characteristics of “fine-thick-fine, the finest at the end” of the cocoon filament size curves were attributed to the composite results that the silkworm spinning mouth opened gradually and spun silk liquid or spinning force decreased continually. Besides, the compound function of Logistic function and quadratic function was applied to simulate the cocoon filament size curve. By means of nonlinear regression analysis and simulation, it is believed that the compound function model has good practicability, and it is expected to become a new generating scheme of cocoon filament size curve description and simulation.
Key words: cocoon filaments size curves; computer simulation of silk reeling; Logistic function; quadratic function; nonlinear regression analysis
若以一定絲长依次摇取一粒茧的茧丝可得到一系列丝段,这些丝段被称为“纤度丝”,将这些纤度丝按获取的顺序(即从茧丝的头端到尾端)编号、称重和换算后可得到一系列有序的纤度值,称为“茧丝纤度序列”或“茧丝纤度曲线” [1] 。茧丝纤度曲线是对茧丝在其长度方向上粗细变化的描述,是蚕茧重要的性状特征,是蚕品种选育和缫丝工艺制定的依据 [2-3] 。有关茧丝纤度曲线的研究已有大量报道 [4-6] ,也被作为概率统计中随机过程的一种实例而广泛关注 [7-9] 。
进一步地,模拟生成茧丝纤度曲线是开展计算机模拟缫丝的前提和基础 [10-12] 。多种方法已被提出用以模拟和生成茧丝纤度曲线,包括阶梯式自回归模型 [13-14] 、二次曲线解析模型 [15] 、有限长度非平稳时间序列模型 [16-17] 、经验模型和其他曲线拟合模型等 [18-19] 。这些方法以茧丝纤度调查时获得的离散茧丝纤度数据为基础,所生成的茧丝纤度数据也是离散化的,其离散间隔与茧丝纤度调查时获得的茧丝纤度数据的离散间隔(即纤度丝的长度,一般为50回或100回,1回=1.125m)一致,但与缫丝中纤度感知器间歇探测纤度的取样间隔不一致,这给计算机模拟缫丝带来不便 [20-22] 。对此,已存在两种解决方案,一是通过插值的方法调整离散间隔,如费万春 [23] 建立的茧丝纤度序列长度的变换方法,其实质是线性或三点二次曲线插值,可用于调整离散间隔。二是采用曲线拟合的方式获得连续化的茧丝纤度曲线,使可获得茧丝任意部位的纤度,如罗军 [24] 用自然边界条件的三次样条函数或直线拟合方法获得的茧丝纤度曲线。
本文从蚕吐丝行为的角度出发,在分析了茧丝纤度曲线形态变化的基础上,将茧丝纤度曲线形态的产生原因归于蚕吐丝时吐丝口的开口大小变化和蚕体内绢丝液或吐丝力变化的复合 [25] 。并用Logistic函数模拟蚕吐丝口的逐步张开对茧丝纤度曲线形态的影响,用二次函数模拟绢丝液或吐丝力的逐渐减弱对茧丝纤度曲线形态的影响,并通过二者的复合模拟茧丝纤度曲线的形态变化,进而建立了茧丝纤度曲线函数模型。进一步地,利用非线性函数回归分析法对函数模型的参数进行分析,提出可用于计算机模拟缫丝的茧丝纤度曲线模拟生成方法。该方法不仅可获得茧丝上任意部位的纤度值,并且通过设置函数参数可更方便地调控茧丝纤度曲线的形态,为下一步进行计算机模拟缫丝提供新的茧丝纤度曲线模拟生产解决方案。
1 蚕吐丝的行为及茧丝纤度曲线形态
蚕吐丝的行为是指蚕将其体内的绢丝液吐出形成茧丝纤维的过程,该过程中绢丝液受丝腺和肌体的收缩挤压而逐渐向吐丝口流动,至吐丝口时,借助蚕体的移动和蚕头部的左右摆动产生牵引作用,使从吐丝口吐出的绢丝液纤维化,形成茧丝 [26-27] 。蚕的这种吐丝行为是其在长期进化中形成的,受蚕品种的影响很大,也与蚕饲育条件、蚕吐丝时的环境等因素密切相关 [28] 。进一步地,茧丝纤度曲线的形态是由蚕吐丝的行为决定的,但即使是同一蚕品种,相同的蚕饲育条件和吐丝环境,不同的蚕个体吐丝形成的茧丝纤度曲线形态依然变化多样,如图1所示。
由图1可知,茧丝纤度曲线的形态虽然各不相同,但基本符合“细-粗-细,最末处最细”的变化趋势。文献[25]认为,这种呈“细-粗-细,最末处最细”变化趋势的茧丝纤度曲线形态是蚕吐丝口逐渐张开和蚕体内绢丝液或吐丝力持续减弱的综合结果。即蚕在吐丝的初期,蚕体内的绢丝液多,吐丝力强,但蚕的吐丝口并未完全张开,导致茧丝初期的纤度并未达到最大值。随着吐丝的进行,虽然蚕体内的绢丝液继续减少,吐丝力量继续减弱,但吐丝口却逐渐张开,综合结果是茧丝纤度逐渐增大,直至最大值。之后,蚕体内的绢丝液持续减少,吐丝力量持续减弱,而吐丝口已张开至最大值,对茧丝纤度变化趋势的影响已十分微弱,故此茧丝纤度又开始逐渐降低。这或许是大部分茧丝的纤度呈“细-粗-细,最末处最细”变化趋势的重要原因,这一原因提示或可采用“S”形函数和单调递减函数分别模拟蚕吐丝口的逐步张开情况和绢丝液或吐丝力的逐渐减弱的情况,并用二者的复合模拟茧丝纤度曲线的形态。
2 函数模型的构建
2.1 Logistic函数
Logistic函数的图形呈“S”形,又被称为sigmoid函数。1844或1845年,法国人皮埃尔·弗朗索瓦·韦吕勒在研究它与人口增长的关系时命名 [30] 。 Logistic 曲线可以模仿生物生长或事物发展中呈现的“S”形变化形态,即起初阶段大致呈指数增长,然后逐渐变得饱和,增加变慢,最后达到成熟时增加停止 [31] 。Logistic函数的表达式 [30] 如下式所示:
f(x)=L1+e -k(x-x 0) (1)
式中:L表示函数曲线的最大值,x 0表示了函数曲线的中心,k表示了曲线的坡度;当L=1,x 0=0,k=1时为其标准式。
Logistic函数在回归分析中有大量的应用 [30] ,也被广泛地应用于生物生长或发展现象的模拟中 [31] 。本文采用Logistic函数模拟蚕吐丝的逐渐开口情况,并探讨Logistic函数的曲线坡度对茧丝纤度曲线形态的影响。
2.2 二次函数
二次函数是最常见的初等函数,其图形是一条抛物线,又被称为抛物线函数。下式为二次函数的顶点式:
g(x)=a(x-l 0) 2+b(2)
式中:a是二次函数的开口率,当a>0时,开口方向向上,坐标(l 0,b)是抛物线的顶点。
前人在对茧丝纤度曲线的研究中指出,茧丝纤度曲线的变化趋势可用二次函数、三次函数、分段函数等形式进行模拟 [32-35] 。特别是,白伦 [15] 在建立茧丝纤度曲线的解析模型时注意到:茧丝纤度曲线从头至尾存在着连续的倾向性变化,且这种连续的倾向性变化随着丝长的延伸其变化率是渐次下降的,而变化率的下降又近似为一定值。这符合开口向上的二次函数的左半部分的变化特征,即其变化率(一阶微分)是渐次下降的,变化率的下降量(二阶微分)是一定值。这些研究提示可采用开口向上的二次函数的左半部分模拟绢丝液或吐丝力的逐渐减弱对茧丝纤度曲线的影响。
2.3 复合函数模型
为了模拟茧丝纤度的这种“细-粗-细,最末处最细”变化趋势,将Logistic函数和二次函数进行复合,如下式所示:
h(x)=f(x)g(x)=L(a(x-l 0) 2+b)1+e -k(x-x 0)
(3)
作為一种函数模型,这里设L=1将不会改变函数的性质,只是使a和b的值有所不同,但a和b属于需要拟合的参数,故这里设L=1是无妨的。另外,为了简化模型,这里设置x 0=0,参数x 0的主要作用是使Logistic函数的图形可沿横轴(x轴)左右横移,这里将x 0=0的实质是将Logistic函数的曲线中心设为0,对曲线的形态并无影响。简化后的复合函数模型如下式所示:
h(x)=a(x-l 0) 2+b1+e -kx (4)
3 函数模型的非线性拟合
为了探讨式(4)所示的函数模型是否适宜于模拟茧丝纤度曲线的形态,在此先以茧丝纤度调查获得的茧丝纤度曲线数据为基础,对函数模型进行非线性拟合,并探讨茧丝纤度曲线形态与函数模型参数之间的关系。
3.1 数据的准备与预处理
1)设图1(a~d)所示茧丝纤度曲线数据均具有如下格式:
S=y 1,0 y 1,1 y 1,2 …y 1,i …y 1,n 1-2 y 1,n 1-1
y 2,0 y 2,1 y 2,2 …y 2,i …y 2,n 2-2 y 2,n 2-1
y j,0 y j,1 y j,2 y j,i y j,n j-2 y j,n j-1
y N,0 y N,1 y N,2 …y N,i …y N,n N-2 y N,n N-1 (5)
式(5)的矩阵中,每行代表1粒茧的茧丝纤度曲线数据,y j,i 表示第j粒茧丝的第i部位的纤度值;n j为用正整数表示的第j粒茧的茧丝长度,同一个庄口茧粒的茧丝长度{n j}符合正态分布;N为调查的茧粒数(图1(a)的N=210,图1(b)的N=200,图1(c)的N=50,图1(d)的N=50)。
2)假设茧丝纤度曲线中的每一个纤度值为其纤度丝长度(记纤度丝长为L T,图1(a~b)的L T=50回=56.25m,图1(c~d)的L T=100回= 112.5m) 内中点的纤度值。
3)茧丝头端与末端的纤度值用各自临近两个纤度值作直线连接延长而得。
4)进一步地,将序号下标转变为茧丝上的长度位置值。
将所有茧丝纤度曲线数据参照步骤2~4进行处理,可完成所有茧丝纤度数据的准备。
3.2 拟合程序说明与参数初始值的设置
3.2.1 函数拟合程序说明
由式(4)可知,该函数模型为非线性函数。本文采用基于Levenberg-Marquardt算法的最小二乘法对函数的参数进行拟合,拟合程序采用基于lmfit包的Python语言编写。
3.2.2 拟合参数的猜测初始值
在采用Levenberg-Marquardt算法的最小二乘法对函数进行拟合时,需要给出拟合参数的合理初始值,这里为了使参数对茧丝纤度曲线形态的模拟具有一定的意义,对参数的初始值作了如下推断。
1)由式(4)可知,记茧丝长为L s,则茧丝纤度曲线的初始纤度和终端纤度分别为:
h(0)=al 2 0+b2(6)
h(L s)=a(L s-l 0) 2+b1+e -kL s (7)
2)由前述分析可知,至繭丝纤度曲线的尾部,Logistic函数对茧丝纤度曲线模型函数变化形态的影响极小,即函数h(x)中的1+e -kL s 部分应近似为一常数,这里设为c,则:
h(L s)≈a(L s-l 0) 2+bc(8)
1+e -kLs ≈c→k≈-log(c-1)L s(9)
由log函数的性质可知,应有c-1>0。作为一种猜测,这里不妨设log(c-1)=1,则:
k=-1L s(10)
c=e+1(11)
3)根据前述分析,式(2)所示的二次函数用于模拟绢丝液或吐丝力的逐渐减弱对茧丝纤度曲线的影响。当a>0时,二次函数开口方向向上,其以l 0为对称轴的左半部是单调下降的,正好符合绢丝液或吐丝力的逐渐减弱的变化,若记茧丝长为L s(L s= n j× L T×1.125),则应有L s≤l 0,这里将参数l 0=L s作为其猜想初始值。
4)当l 0=L s,c=e+1时,h(L s)≈b1+e→b≈ h(L s) (1+e),故此,这里将b=h(L s)(1+e)作为参数b的猜测初始值。
5)当l 0=L s,b=h(L s)(1+e)时,由式(9)可推知:
a=2h(0)-h(L s)(1+e)L s,故此,这里将
a=2h(0)-h(L s)(1+e)L s作为其猜测初始值。
综上,只要知道茧丝纤度序列的初始纤度值、终端纤度值和茧丝长,即可得到函数参数的猜测初 始值。
3.3 函数拟合的结果与分析
参照3.1对纤度曲线数据进行预处理和3.2所述的程序及参数设置方法,对图1(a~d)所示庄口的茧丝纤度曲线逐一进行拟合,并统计其参数的分布特征,结果如图2所示。其中,结果中拟合优度的计算公式如下式所示:
R 2=1-∑(y-y *) 2∑y 2(12)
式中:y为实际茧丝纤度曲线数据,y *为拟合函数计算得到的拟合数据。
由图2可知,四个庄口的拟合优度分布虽有不同,但均得到较好的拟合效果。而拟合优度分布的差异与庄口茧丝的样本量和部分茧丝呈现的特殊形态有关。
4 茧丝纤度曲线的模拟生成方法
4.1 函数参数与茧丝纤度曲线特征纤度值之间的关系
4.1.1 公式推演
式(4)所示的函数,可通过茧丝纤度曲线的一些特征值计算得到函数模型参数a,l 0、b和k。这里以茧丝纤度曲线的初始端纤度、终端纤度、最大纤度和茧丝长为特征,作如下推演。
首先,将复合函数h(x)对自变量x开导数, 可得:
h(x)x=e kx (bk+a(x-l 0)(2+2e kx -kl 0+kx))(1+e kx ) 2(13)
若令h(x)x=0,则可求出茧丝纤度曲线最大纤度位置。虽然式(13)所示的零点位置不易直接求出,但根据函数模型的含义,x=l 0为二次函数的顶点,该处为二次函数的极小值位置,而Logistic函数在x=l 0处已对函数h(x)的形态几乎没有影响,故此可知x=l 0可近似为函数h(x)的极小值位置,即当x=l 0时,h(x)x=0。进一步地,若使x=l 0处h(x)x=0,则必有bk=0,至此,出现三种情况:
1)k=0,b≠0,则式(4)变为:
h 1(x)=a(x-l 0) 2+b2(14)
由式(14)可知,茧丝纤度曲线函数蜕变为二次函数,其中h 1(0)=al 2 0+b2、h 1(L s)=a(L s-l 0) 2+b2。
此时,可假设l 0=L s,则b=2h 1(L s),a=(2h 1(0)-2h 1(L s))L 2 s。
2)k=0,b=0,则式(4)变为:
h 2(x)=a(x-l 0) 22(15)
此时有h 2(0)=al 2 02、h 2(L s)=a(L s-l 0) 22。
解此方程组可得l 0=L s1±h 2(L s)h 2(0)、a=2h 2(0)l 2 0。
3)k≠0,b=0,则式(4)变为:
h 3(x)=a(x-l 0) 21+e -kx (16)
此时有:
h 3(0)=al 2 02(17)
h 3(L s)=a(L s-l 0) 21+e -kLs (18)
另外,此时函數h 3(x)存在除x=l 0外的另一个极值点,即极大值点,使h 3(x)x=0。由式(13)可知,只有
2+2e kx -kl 0+kx=0时,可使h 3(x)x存在另一个零点。假设x=t 时h 3(x)x=0,此时茧丝纤度曲线的纤度值最大,记y max 为其最大纤度值,则有:
h 3(t)=a(t-l 0) 21+e -kt =y max (19)
2+2e kt -kl 0+kt=0(20)
综上式(17)~(20)构成了一个非线性方程组,利用Python语言scipy包中optimize模块的fsolve函数,可求出此非线性方程组的数值解,从而得到参数a,l 0、b和k。
4.1.2 拟合验证
为了验证所推导的模型参数值是否合理,以推演的模型计算值为横坐标,以函数拟合后获得的最优拟合值为纵坐标,分别绘制四个庄口结果的散点图,如图3所示。
由图3可知,除极少数的异常点外,计算获得的模型参数与拟合最优参数值之间存在着密切的正相关关系,说明计算获得的模型参数具有良好的适 用性。
4.2 茧丝纤度曲线的模拟生成步骤
基于以上的分析,可将茧丝纤度曲线的模拟生成方法总结如下:
1)对所要模拟的蚕茧庄口进行茧丝纤度调查。
2)根据3.1所述的方法,对调查获得的茧丝纤度曲线数据进行预处理。
3)分别统计该庄口茧丝纤度曲线的初始端纤度均值(μ 0)及方差(σ 0)、终端纤度的均值(μ n)及方差(σ n)、茧丝长度的均值(μ L)及方差(σ L)、最大纤度的均值(μ ymax )及方差(σ ymax )。
4)基于步骤3所得的庄口茧丝纤度曲线特征,根据正态分布抽样原理,分别抽样获得初始端纤度值、终端纤度值、茧丝长度值、最大纤度值。
5)根据步骤4所得抽样值组,分别计算函数模型参数a,l 0、b和k。
6)根据函数模型式(4)和所得参数a,l 0,b和k,获得一条茧丝纤度曲线。重复步骤(4)~(6)可获得无数条符合所调查庄口茧丝纤度特征的茧丝纤度曲线函数组。
4.3 茧丝纤度曲线模拟生成效果
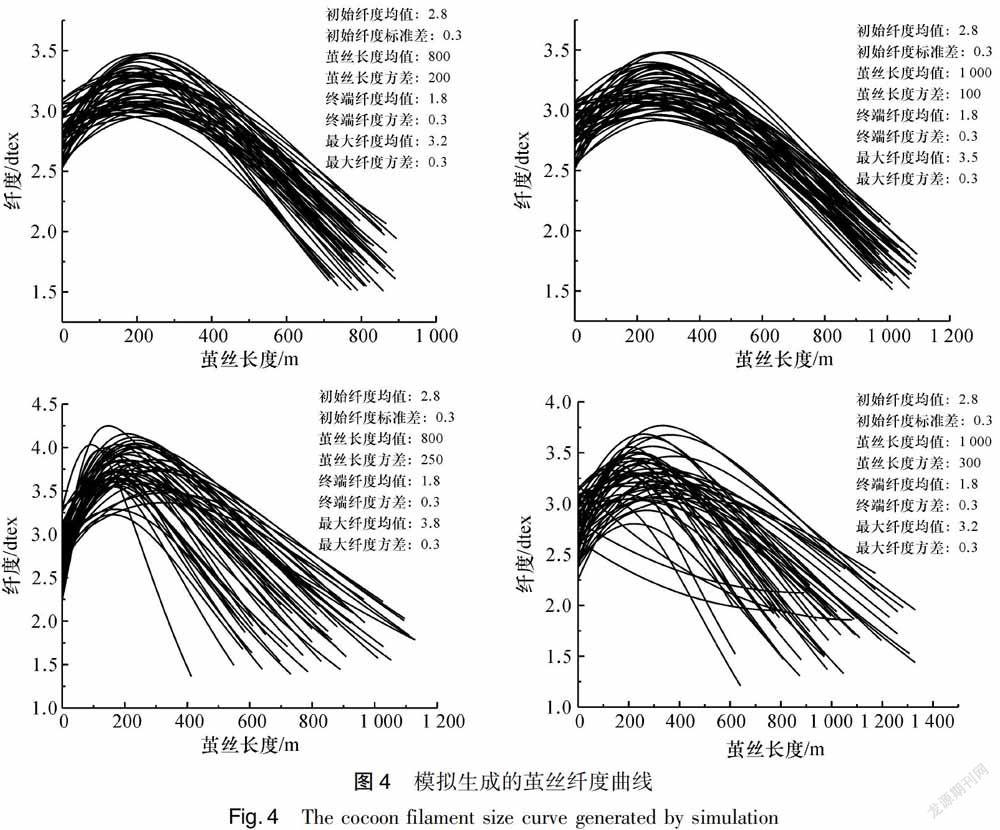
根据4.2所述方法,可生成一系列茧丝纤度曲线,如图4所示为4组不同参数设置值产生的茧丝纤度曲线图形。由图4可知,所生成的茧丝纤度曲线的形态特征与实际纤度调查获得的茧丝纤度曲线形态特征近似,说明该模拟方法具有良好的模拟生成效果。
5 结 语
本文在分析了茧丝纤度曲线形态的基础上,从蚕吐丝行为的角度出发,将茧丝纤度曲线形态的产生原因归于蚕吐丝时吐丝口的开口大小变化和蚕体内绢丝液或吐丝力变化的复合。并用Logistic函数模拟蚕吐丝口的逐步张开对茧丝纤度曲线的影响,用二次函数模拟绢丝液或吐丝力的逐渐减弱对茧丝纤度曲线的影响,并通过二者的复合模拟茧丝纤度曲线的形态变化,进而建立了茧丝纤度曲线函数模型。通过理论分析和非线性函数回归分析可知:
1)所建立的茧丝纤度曲线函数模型具有模拟茧丝纤度曲线形态的可行性和合理性。
2)茧丝纤度曲线的初始端纤度值、终端纤度值、茧丝长度值和最大纤度值与函数模型的参数密切 相关。
3)通过模拟生成茧丝纤度曲线的初始端纤度值、终端纤度值、茧丝长度和最大纤度值可获得茧丝纤度曲线函数模型的参数,进而获得茧丝纤度曲线函数。
4)建立了茧丝纤度曲线模拟生成方法,该方法可通过设置函数参数方便地调控茧丝纤度曲线的形态,为下一步进行计算机模拟缫丝提供新的茧丝纤度曲线解决方案。
5)就庄口茧丝纤度曲线的统计特征的模拟,有待进一步深入研究。
参考文献:
[1]荣光远. 制丝工艺设计与质量管理[M]. 北京: 中国纺织出版社, 1993.
RONG Guangyuan.Process Design and Quality Management of Filature [M]. Beijing: China Textile and Apparel Press, 1993.
[2]赵巧玲, 魏兆军, 夏定国, 等. 家蚕茧丝纤度性状基因效应分析[J]. 中国蚕业, 2001(1): 43.
ZHAO Qiaoling, WEI Zhaojun, XIA Dingguo, et al. Analysis of the gene effect of Bombyx mori silkworm cocoon filament [J]. Sericulture in China, 2001(1): 43.
[3]郭冬阳, 谭端, 代方银. 家蚕茧丝纤度的研究现状及相关探究[J]. 蚕学通讯, 2014, 34(4): 18-22.
GUO Dongyang, TAN Duan, DAI Fangyin. The current status of researches of silkworm cocoon silk fineness and related studies [J]. Newsletter of Sericultural Science, 2014, 34(4): 18-22.
[4]盛井龙. 基于虚拟仪器的茧丝细度连续测量的研究[D]. 苏州: 苏州大学, 2008.
SHENG Jinglong. The Study of Continuous Testing for the Fineness of Cocoon Based on Virtual Instrument [D]. Suzhou: Soochow University, 2008.
[5]黄继伟, 洪基武, 林海涛, 等. 茧丝强力序列的测试与分析[J]. 丝绸, 2014, 51(2): 30-34.
HUANG Jiwei, HONG Jiwu, LIN Haitao, et al. Test and analysis of cocoon filament strength sequence [J]. Journal of Silk,2014,51(2):30-34.
[6]费万春, 描述茧丝纤度序列的理论模型[J]. 丝绸, 2007(2): 19-21.
FEI Wanchun. Theoretical model for describing size series of cocoon filament [J]. Journal of Silk, 2007(2): 19-21.
[7]鲁星星, 费万春. 时间序列分析上的丝绸之路[J]. 现代丝绸科学与技术, 2011(1): 38-40.
LU Xingxing, FEI Wanchun.The silk road above on time series analysis [J]. Modern Silk Science and Technology, 2011(1): 38-40.
[8]周桂霞. 基于函数系数自回归的非线性时间序列分类[D]. 苏州: 苏州大学, 2012.
ZHOU Guixia. Classification of Nonlinear Time Series using Functional-Coefficient Regression [D]. Suzhou: Soochow University, 2012.
[9]洛鍵. 基于茧丝纤度序列的多总体分类判别及其比较[D]. 苏州: 苏州大学, 2011.
LUO Jian. The Classification and Discrimination Methods among Several Populations Based on Size Series of Cocoon Filament and Their Comparison [D]. Suzhou:Soochow University, 2011.
[10]张晓光, 姚跃飞. 缫丝模拟系统的设计[J]. 浙江工程学院学报, 2004, 21(3): 169-173.
ZHANG Xiaoguang, YAO Yuefei. Design of simulation system about silk-reeling [J]. Journal of Zhejiang Institute of Science and Technology, 2004, 21(3): 169-173.
[11]罗军. 定纤自动缫丝的计算机模拟及其应用[J]. 丝绸, 2006(11): 42-45.
LUO Jun. Computer simulation and application of automatic reeling with fixed size [J]. Journal of Silk, 2006(11): 42-45.
[12]黎霞. 定纤缫丝及质量检验模拟系统研究[D]. 苏州: 苏州大学, 2002.
LI Xia. System of Simulation Fixed Size Silk Reeling Process and Assessing Silk Quality [D]. Suzhou: Soochow University, 2002.
[13]白伦, 谢佳, 李林甫, 等. 茧丝纤度曲线的模拟生成[J]. 苏州丝绸工学院学报, 1998, 18(1): 1-8, 26.
BAI Lun, XIE Jia, LI Linfu, et al. Generation of the size curve of cocoon filament by computer simulation [J]. Journal of Suzhou Institute of Silk Textile Technology, 1998, 18(1): 1-8, 26.
[14]白伦, 谢佳, 李林甫, 等. 模拟茧丝纤度曲线的统计特征[J]. 苏州丝绸工学院学报, 1999, 19(1): 1-7.
BAI Lun,XIE Jia,LI Linpu,et al.Statistical characters of the size curve of cocoon filament by computer simulation [J]. Journal of Suzhou Institute of Silk Textile Technology, 1999, 19(1): 1-7.
[15]白伦, 费万春, 罗军, 等. 茧丝纤度曲线的解析模型及其在模拟缫丝中的应用[J]. 蚕业科学, 2002, 28(3): 233-237.
BAI Lun, FEI Wanchun, LUO Jun, et al. An analytical model of the size curve of cocoon filament and its application to the simulation text [J]. Acta Sericologica Sinica, 2002, 28(3): 233-237.
[16]费万春. 茧丝纤度曲线的预测研究[D]. 苏州: 苏州大学, 2002.
FEI Wanchun. Study on Forecasting Size Curves of Cocoon Filaments [D]. Suzhou: Soochow University, 2002.
[17]黄洁. 有限长非平稳时间序列的模拟方法[D]. 苏州: 苏州大学, 2012.
HUANG Jie. A Simulation Method for Finite Non-Stationary Time Series [D]. Suzhou: Soochow University, 2012.
[18]胡征宇, 俞海峰.茧丝线密度变化的拟合与预测[J]. 纺织学报, 2008, 29(10): 29-33.
HU Zhengyu, YU Haifeng. Fitting and forecasting the silk size curve [J]. Journal of Textile Research, 2008, 29(10): 29-33.
[19]唐映珊, 陆鹏祥. 利用经验公式预测茧丝纤度和粒茧丝长[J]. 广西蚕业, 2010, 47(2): 62-66.
TANG Yingshan, LU Pengxiang. The forecast for length and size of cocoon filament by the empirical formula [J]. Guangxi Sericulture, 2010, 47(2): 62-66.
[20]张淑娜, 姚跃飛, 张晓光, 等. 定纤自动缫丝机的计算机模拟系统设计[J]. 丝绸, 2005(10): 19-21.
ZHANG Shuna, YAO Yuefei, ZHANG Xiaoguang, et al. Design of computer simulation system for automatic reeling with fixed size [J]. Journal of Silk,2005(10): 19-21.
[21]罗军. 定粒生丝纤度管理研究[D]. 苏州: 苏州大学, 2002.
LUO Jun. Study on Management of Raw Silk Size in Fixed Cocoon Number Reeling Process [D]. Suzhou: Soochow University, 2002.
[22]吴春丽. 定粒配茧缫丝的建模及模拟研究[D]. 苏州: 苏州大学, 2005.
WU Chunli. The Study on Modeling and Simulating of Reeling Process with Fixed Number of Matched Cocoons [D]. Suzhou:Soochow University, 2005.
[23]费万春, 罗军, 黎霞, 等. 茧丝纤度序列长度的变换方法[J]. 苏州大学学报(工科版), 2003, 23(2): 17-23.
FEI Wanchun, LUO Jun, LI Xia, et al. On the length transform of size series of cocoon filaments [J]. Journal of Soochow University (Engineering Science Edition), 2003, 23(2): 17-23.
[24]罗军, 常春枝. 茧丝纤度曲线模型在模仿缫丝上的应用[J]. 苏州丝绸工学院学报, 2000, 20(1): 36-42.
LUO Jun, CHANG Chunzhi. Application of the model of cocoon filament size curve to the simulation of the silk-reeling[J]. Journal of Suzhou Institute of Silk Textile Technology, 2000, 20(1): 36-42.
[25]徐水, 胡征宇. 茧丝学[M]. 北京: 高等教育出版社, 2016.
XU Shui, HU Zhengyu. Cocoon Silk Science[M]. Beijing: Higher Education Press,2016.
[26]陈文兴, 傅雅琴, 江文斌. 蚕丝加工工程[M]. 北京: 中国纺织出版社, 2013.
CHEN Wenxing, FU Yaqin, JIANG Wenbin. Silk Processing Engineering [M]. Beijing:China Textile and Apparel Press,2013.
[27]ASAKURA T, UMEMURA K, NAKAZAWA Y, et al. Some observations on the structure and function of the spinning apparatus in the silkworm bombyx mori [J]. Biomacromolecules, 2007, 8(1): 175-81.
[28]KUMAR C M K. Development of Bivoltine Silkworm Breeds of Bombyx Mori L with Reference to Cocoon Filament Characters [D]. Mysore: University of Mysore, 2010.
[29]陸开阳. 生丝纤度控制理论与纤度质量辅助分析软件开发[D]. 苏州: 苏州大学, 2007.
LU Kaiyang.Control Theory of Raw Silk Size and Computer Aided Analysis Software Development of Size Quality [D]. Suzhou: Soochow University, 2007.
[30]MENARD S. 应用Logistic回归分析[M]. 2版. 李俊秀, 译. 上海: 格致出版社, 2016.
MENARD S. Applied Logistic Regression Analysis[M]. 2nd Edi.Translated by LI Junxiu. Shanghai: Truth and Wisdom Press, 2016.
[31]张显真, 杨晓峰. 温室水果黄瓜叶片生长规律研究[J]. 气象与减灾研究, 2008, 31(3): 43-47.
ZHANG Xianzhen, YANG Xiaofeng. Study on disciplinarian of greenhouse cucumber leaf growth [J]. Methorology and Disaster Reduction Research, 2008, 31(3): 43-47.
[32]胡琛瑜. 茧丝纤度标准曲线的探讨[J]. 丝绸, 1992(12): 14-15.
HU Chenyu. Discussion on the standard curve of cocoon filament size [J]. Journal of Silk, 1992(12): 14-15.
[33]胡琛瑜. 茧丝纤度标准曲线在工艺设计中的应用[J]. 丝绸, 1993(5): 20-22.
HU Chenyu. Application of the standard curve of cocoon filament size in process design [J]. Journal of Silk, 1993(5): 20-22.
[34]胡琛瑜. 茧丝纤度特征数计算方法的探讨及外、中、内层的划分[J]. 丝绸, 1993(10): 37-38.
HU Chenyu. Discussion on the characteristic number of cocoon filament size curve and the division of the outer, middle and inner layer [J]. Journal of Silk, 1993(10): 37-38.
[35]梁烈峰. 茧丝纤度曲线的拟合及其应用[J]. 现代纺织技术, 1998,6(2): 33-36.
LIANG Liefeng. The fitting and application of cocoon filament size curve [J]. Modern Textile Technology, 1998,6(2): 33-36.
