基于RNN模型的工业机器人故障可跟踪预测方法

李丹婷

摘要：针对工业机器人故障导致的生产浪费和安全问题，提出了一种基于递归神经网络（RNN）的工业机器人故障可跟踪预测方法。结合RNN模型的时间序列自适应学习能力，设计了基于聚类分析的关键影响因子提取方法，提升了预测的召回率和准确率，借助于专家系统的解释器机制，实现了故障定位功能。实验表明，相对于无关键影响因子提取的RNN模型，此方法将故障预测能力提升了1倍以上，且最多能够提前20 min给出故障告警，解释器故障定位的平均准确率为87.11%，为维护人员发现和解决故障提供了有力的保障。

关键词：故障预测；关键影响因子提取；RNN；解释器；工业机器人

中图分类号：TP242文献标志码：A文章编号：1008-1739（2018）02-68-4

Traceable Fault Prediction Method for Industrial Robot Based on RNN Model

LI Danting

（Nanjing ESTUN Automation Corp.， Ltd， Nanjing Jiangsu 210000， China）

0引言

随着智能制造的快速发展，工业机器人应用也越来越广泛，发生故障不但会导致生产停滞，甚至将威胁人们的生命，如何有效预测工业机器人的故障，是保障工业机器人安全稳定运行的重要手段。

机器学习是人工智能领域最受关注的研究课题之一，如SVM[1-2]、CNN[3-4]及RNN[5-7]等，已经成功应用于垃圾邮件过滤、图像识别、语音处理、文本分析、OCR及网络入侵检测等多个领域，极大地推动了现代社会智能化进程。RNN是机器学习中应用广泛的一个模型，它的隐藏层具有记忆功能，能够按时间顺序将前后影响因素综合起来分析，从而可以综合工业机器的历史情况分析系统，为故障预测提供全面支撑。但RNN并不具备解释机制，当检测到可能出现故障时难以追溯原因。

本文将以RNN技术为基础，结合解释器机制，提出了一种面向工业机器人故障的可跟踪预测方法。该方法基于聚类分析对工业机器人故障的关键因子进行提取，提升了工业机器人故障预测的效率和准确性，同时利用解释器机制，实现了故障预测的可跟踪性。

1递归神经网络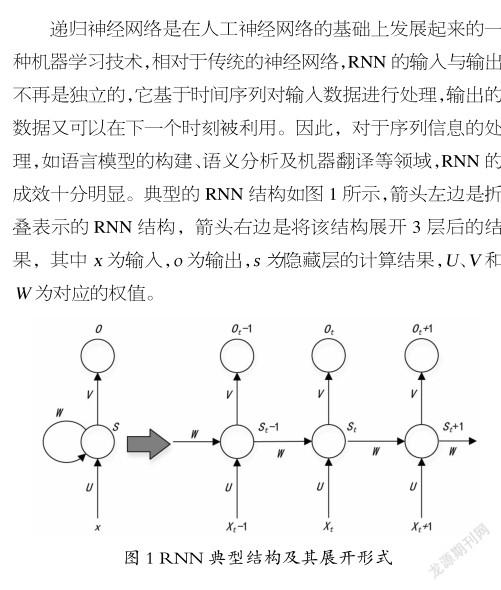

2基于RNN模型的故障可跟踪预测方法

由于工业机器人操作精细化程度高，故障预测实时性要求强，因此，本文对故障的影响因子进行了筛选，剔除了影响较弱的因素，减少了RNN需要的参数，以提升模型的构建、更新及预测性能。同时，便于维护人员定位故障，在RNN正向计算的过程中，保留了最近2次的中间计算结果，以便于在故障出现时通过解释器的对比分析，将可能的故障点反馈给维护人员。基于RNN模型的故障可跟踪预测方法的基本框图如图1所示，包括模型训练和故障预测2个部分。

（1）模型训练主要通过训练数据实现预测模型的构建与更新。在系统运行前，它以历史记录的工业机器人系统故障和正常状态数据为初始训练数据，通过关键影响因子提取处理后，选取与故障发生最紧密的影响因子作为特征向量，使用RNN进行模型训练。当系统运行后，系统的状态信息和实际的故障预测结果将传输到训练数据库，以便于模型的重新训练与更新，提升预测模型的鲁棒性。

（2）故障预测主要通过故障预测模型对系统出现故障的可能性进行预测，并将预测的依据通知给维护人员，主要包括以下2个步骤：

①根据关键影响因子提取过程获得的因子，对系统状态信息进行预处理，提取其中的关键因子进行序列化，转换为故障预测模型可以接受的数据格式；

②故障预测模型对序列化后的数据进行处理，并保留最近2次计算的中间计算结果；如果预测到系统故障，则由解释器分析最近2次的中间计算结果，根据故障前后激活点的不同，形成故障点预测报告，传递给维护人员核实。

在该方法中，关键影响因子的提取和解释器的增加是保障故障预测性能、提升预测模型鲁棒性和实现故障可跟踪的重要手段。

2.1基于聚类分析的关键影响因子提取方法

影响因子主要用来表征系统状况的正常情况，为获得准确有效的关键影响因子，采用基于聚类分析的提取方法。

定义1：2个聚类的边缘点：如果一个点到聚类中心1的距离与到聚类中心2的距离的比值小于2并且大于0.5，则认为该点是这2个聚类的边缘点。

定义2：聚类离散率：聚类边缘点数与总点数的比例。关键影响因子提取方法包括以下步骤：

①根据工业机器人的功能特性和工作环境，构建故障预测的影响因子初始集合，主要包括环境因素（如温度、湿度及海拔等）、电气特征（如电压、电流及时钟频率等）、物理特性（压力和力矩等）以及其他关键信号等；对于训练数据集中的每个数据，计算其影响因子相对于运行状态的信息熵[8]，进而根据式（1）计算每个因子的权值；

2.2基于隐藏节点时间序列状态差异的故障点提取方法

解释器最主要的工作是找出故障点。由于本文修改了RNN的計算过程，保存了连续2次RNN计算的中间结果-1和，因此可以知道每次结果产生时哪些状态是激活的，哪些状态是未激活的，而2次中间结果正好能够记录故障产生前后的2个状态。通过对比这2个状态下激活因子的差异，解释器就可以确定故障是因为哪些因子发生变化引起的，从而可以给出相应的故障点，为维护人员提供支撑。

提取故障點的具体算法如下：输入：

其中和分别为和故障前后各隐藏节点的激活状态，

为从隐藏节点到影响因子的映射关系，的每一个元素0表示影响隐藏节点0取值的输入因子集合（忽略权值小于阈值的输入因子，实验中该阈值取值为0.01）。

3实验结果及分析

以TensorFlow[10]为RNN计算的基本框架，以某机器人公司6个类别工业机器人系统的运行状态信息库为基础，抽取了前10天的运行数据作为初始训练数据（其中故障记录52条），初始的影响因子为全部的318个影响因子。设置关键影响因子提取方法中最大迭代次数为100，候选集提取的聚类离散度阈值设置为0.1，按照本文方法构建相应的预测模型。

本文方法与未进行关键影响因子提取的RNN模型对剩余的71个故障的预测时间曲线如图3所示，由于通用RNN未对关键影响因子进行过滤，分析的影响因子多，噪声也多，50%以上的节点未达到故障预测的目的（提前发现时间为0的节点），即使能够对故障进行预测，但由于处理无关影响因子多、模型更新处理速度慢的原因，最快的提前发现时间不足10 min，而本文方法对剩余的71个故障都进行了准确预测，刚开始的故障节点，故障预测与故障实际出现的时间相差不大，约为3 min左右。随着时间的增加，训练数据的积累，模型的快速调整，故障预测的速度有了明显的提升，最长的甚至可以提前20min，为预防故障的发生提供了充足的时间。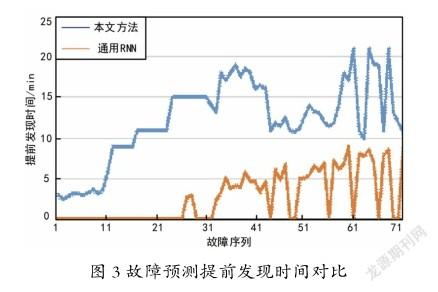

本文方法故障定位的精度如图4所示，6类工业机器人故障定位的平均准确率约为87.11%，最高可达93.33%，为维护人员定位故障点提供了有力的支撑。

4结束语

工业机器人的广泛应用，一方面大幅度节约了人力成本、保证了产品的质量和提升了生产效率，但另一方面，由于人们对工业机器人的过度依赖，一旦发生故障将产生严重的后果。针对工业机器人可能发生的故障，设计了一种基于RNN模型的工业机器人故障可跟踪预测方法，通过关键因子提取和解释器的结合，有效地提升了故障预测的准确率，为及早定位并解决工业机器人故障，保障生产经营的顺利进行提供了有力的支持。

参考文献

[1] Zhang Y，Li B，Lu H，et al.Sample-Specific SVM Learning for Person Re-identification[C]// IEEE Conference on Computer Vision and Pattern Recognition，Las Vegas：USA，July 5，2016： 1278-1287.

[2] Kumar M， Gromiha M M， Raghava G P. SVM based Prediction of RNA-Binding Proteins Using Binding Residues and Evolutionary Information[J].Journal of Molecular Recognition，2015，24（2）：303-313.

[3]李彦冬，郝宗波，雷航.卷积神经网络研究综述[J].计算机应用，2016，36（9）：2508-2515.

[4] Tajbakhsh N， Suzuki K. Comparing Two Classes of End-to-End Machine-Learning Models in Lung Nodule Detection and Classification： MTANNs vs.CNNs[J]. Pattern Recognition，2016.

[5] Jain A， Zamir A R， Savarese S， et al.Structural-RNN： Deep Learning on Spatio-Temporal Graphs[C]//IEEE Conference on Computer Vision and Pattern Recognition. IEEE Computer Society， 2016：5308-5317.

[6] Wang J， Yang Y， Mao J， et al. CNN-RNN： A Unified Framework for Multi-label Image Classification[C]// IEEE Conference on Computer Vision and Pattern Recognition，Las Vegas：USA，July 5，2016：2285-2294.

[7]张舸，张鹏远，潘接林，等.基于递归神经网络的语音识别快速解码算法[J].电子与信息学报，2017，39（4）：930-937.

[8] Núnez J A，Cincotta P M，Wachlin F C.Information entropy[J].Celestial Mechanics & Dynamical Astronomy，1996，64（1-2）：43-53.

[9] Deng Z，Zhu X，Cheng D，et al.Efficient kNN Classification Algorithm for Big Data[J].Neurocomputing，2016，195（C）： 143-148.

[10] Abadi M，Barham P，Chen J，et al.TensorFlow： A System for Large-Scale Machine Learning[C]//Usenix Conference on Operating Systems Design and Implementation，USENIX Association，San Jose，USA，May 26，2016：265-283.