WEIGHTED COMPOSITION OPERATORS ON THE HILBERT SPACE OF DIRICHLET SERIES∗

Maofa WANG(王茂发)

School of Mathematics and Statistics,Wuhan University,Wuhan 430072,China

E-mail:mfwang.math@whu.edu.cn

Xingxing YAO(姚兴兴)†School of Science,Wuhan Institute of Technology,Wuhan 430205,China

E-mail:xxyao.math@whu.edu.cn

Fangwen DENG(邓方文)

Wuhan Institute of Physics and Mathematics,Chinese Academy of Sciences,Wuhan 430071,China

E-mail:fwdeng@wipm.ac.cn

Abstract In this paper,we study weighted composition operators on the Hilbert space of Dirichlet series with square summable coefficients.The Hermitianness,Fredholmness and invertibility of such operators are characterized,and the spectra of compact and invertible weighted composition operators are also described.

Key words weighted composition operator;Hermitianness;Fredholmness;invertibility;spectrum

1 Introduction

Let H be the Hilbert space of Dirichlet series with square summable coefficients

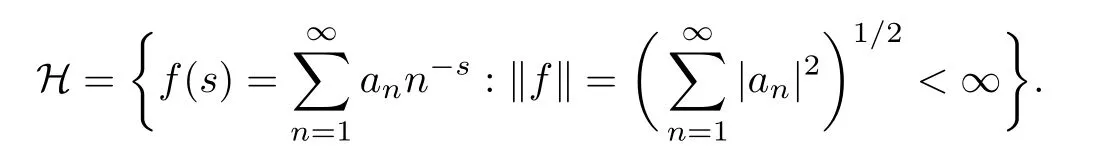
By the Cauchy-Schwarz inequality,the functions in H are all analytic on the half-plane C1/2(where,for θ∈ R,Cθ={s∈ C:Res> θ}and C+=C0).In the process,we also encounter the space D of functions f,which in some(possibly remote)half-plane admit representation by a convergent Dirichlet series

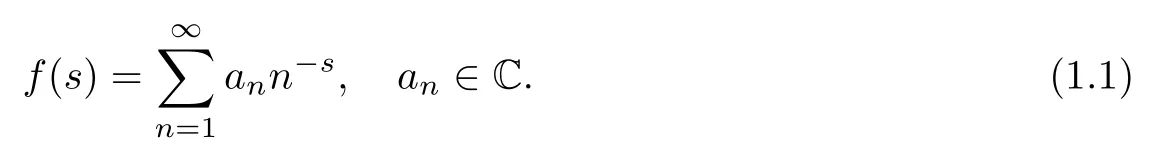
Let f be a Dirichlet series of form(1.1).There are several abscissas attached to it

It is easy to see that−∞ ≤ σc(f)≤ σu(f)≤ σa(f)≤ +∞ for all f of form(1.1).We will also need the abscissa of regularity and boundedness σb(f),which is the infimum of those σ ∈ R for which the function f defined as in(1.1),possibly by analytic continuation from a smaller half-plane,is analytic and bounded on Cσ.An important result of Bohr[3]is that σu(f)and σb(f)coincide.We also recall that a series in D actually converges absolutely in the half-plane one unit to the right of the half-plane of convergence.

As usual,we denote by H∞(C+)the set of all bounded analytic functions on C+,and by U the subset of H∞(C+)of functions belonging to D.In particular,Theorem 7 of[1]asserted that the set of multipliers of H is U.

Throughout this paper,a weighted composition operator WΨ,Φon H takes an analytic function f ∈ H to the analytic function Ψ ·f ◦ Φ,where Ψ is an analytic function on the halfplane C1/2and an analytic map Φ :C1/2→ C1/2defines a composition operator on H.Clearly,there are two particularly interesting special cases of such operators:the composition operator CΦby taking Ψ =1 and the multiplication operator TΨby putting Φ =id,the identity function of C1/2.It should be mentioned that,by the closed graph theorem,every composition operator CΦ:H→H is automatically bounded(see[8]).Moreover,the following comes from[8,14],which gives some explicit properties of composition symbols.

Theorem A An analytic function Φ :C1/2→ C1/2determines a bounded composition operator CΦ:H→H if and only if

where c0is a nonnegative integer,andconverges uniformly in Cǫfor every ǫ>0 and has the following mapping properties.

(a)If c0=0,then ϕ(C+)⊂ C1/2.

(b)If c0≥ 1,then either ϕ ≡ 0 or ϕ(C+)⊂ C+.

Weighted composition operators,on classical spaces of analytic functions on the unit disk of the complex plane C,were fundamental objects of study in analysis that arise naturally in many situations;e.g.,[7,12,17].Moreover,such operators arose in the study of commutants of multiplication operators,and they played a crucial role in the theory of dynamical systems as well.We refer to monographs by Cowen-MacCluer[6],Shapiro[16]and Zhu[19]for general information of composition operators on classical spaces of analytic functions on the unit disk.The problem of relating operator theoretic properties of WΨ,Φto function theoretic properties of Ψ and Φ was a subject of great interest for quite some time;e.g.,[4,5,9,10],on those classical spaces.The purpose of this paper is to generalize some results on them to the case H.

This paper is organized as follows.Section 2 includes the background material needed to make this paper as self-contained as possible.Section 3 characterizes the Hermitian weighted composition operators on H.Moreover,the Fredholmness and invertibility of such operators are characterized completely in Section 4.Finally,the spectra of compact and invertible weighted composition operators are described in Section 5.

2 Background Material

Assume that Ψ is analytic on C1/2and an analytic map Φ :C1/2→ C1/2defines a composition operator on H.If the weighted composition operator WΨ,Φis bounded on H,then Ψ ∈ H and Φ satisfies the conditions given in Theorem A(call this Φ a c0-symbol).As we know,the reproducing kernel at w∈C1/2for H is given by Kw(s)=ζ(w+s)for Res>1/2,and its norm equals ζ(2Rew)1/2,where ζ is the Riemann zeta functionRecall that the function ζ satisfies the identity

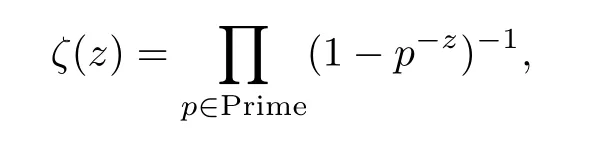
and has no zeros in C1,where and in the following,we use the notation “Prime” to denote the set of all prime numbers.It has zeros at z= −2,−4,−6,···called the trivial zeros,and all other zeros lie in 0≤Rez≤1.If we denote by W∗Ψ,Φthe adjoint of WΨ,Φwhenever it is bounded,then for w∈C1/2,

Let Φ be an analytic self-map of C1/2.For all n ∈ N we denote the n-th iterate of Φ by Φn,that is

For n=0 we set Φ0:=id,the identity function of C1/2.If Φ is a biholomorphic map of C1/2,then we denote Φ−n:=(Φ−1)n.It is easy to check that

for all n≥1,f∈H and s∈C1/2.Hence(WΨ,Φ)n=Ψ(n)CΦn,where

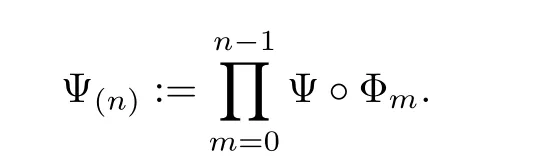
Also for n=0 we set Ψ(0)=1 for convenience.

The following lemmas are from[1]and[8],respectively.

Lemma 2.1 Let Φ(s)=c0s+ϕ(s)be an analytic self-map of C+.If Φ(s)6=s+iτ,τ∈ R,then there exist η >0 and ǫ>0 such that Φ(C1/2−ǫ) ⊂ C1/2+η.

Lemma 2.2 Let m be a positive integer,and letbe a Dirichlet series from the class D,starting from the index m.Then msf(s)→amuniformly as Res→+∞.

If T is an operator on a Hilbert space H,we denote by σ(T)its spectrum

and σp(T)its point spectrum

where IHis the identity operator on H.Also we denote by r(T)its spectral radius:r(T)=sup{|λ|:λ ∈ σ(T)}.The following is Lemma 7.17 in[6],which allows us to reduce the eigenvalue problem to a finite dimensional problem.

Lemma 2.3 Suppose H is a Hilbert space with H=K⊕L,where K is finite dimensional and C is a bounded operator on H that leaves K or L invariant.If the operator C has the matrix representation

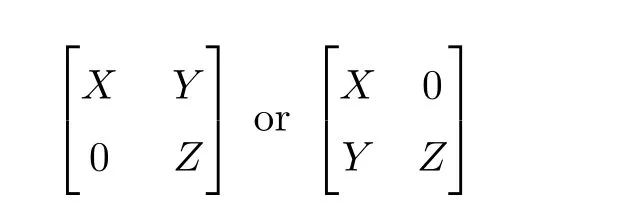
with respect to this decomposition,then σ(C)= σ(X)∪ σ(Z).

3 Hermitianness

We first characterize the Hermitian composition operators on H.

Lemma 3.1 Let Φ be a c0-symbol.Then the composition operator CΦis Hermitian on H if and only if Φ(s)=s+c with c≥ 0.

Proof The sufficiency is trivial,so it is needed only to prove the necessity.To this end,we assume that CΦis Hermitian on H,then it is normal.It follows from Theorem 15 in[1],Φ(s)=s+c with Rec≥ 0.In this case,it is obvious that

and thus

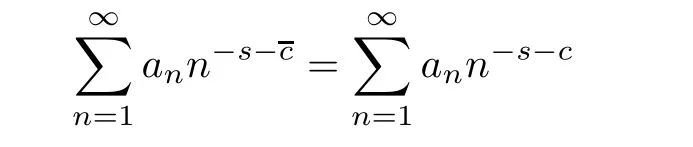
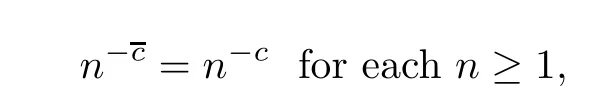
Here,we will distinguish between the two cases c0=0 and c06=0.

for every prime number p and s∈C1/2.

Proof Let Kwbe the reproducing kernel for H at w ∈ C1/2.If WΨ,Φis Hermitian on H,then(WΨ,ΦKw)(s)=(W∗Ψ,ΦKw)(s),i.e.,

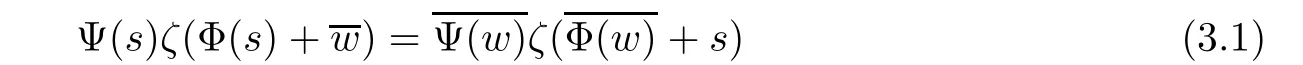
for each s,w∈C1/2.Since c0=0,then the left hand side of(3.1)is

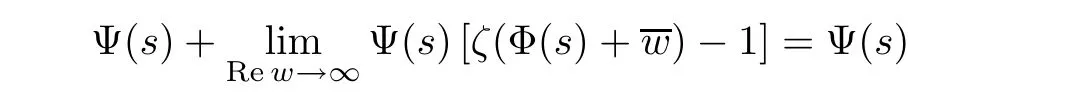
for Res large enough.Indeed,it follows from Lemma 2.2 that

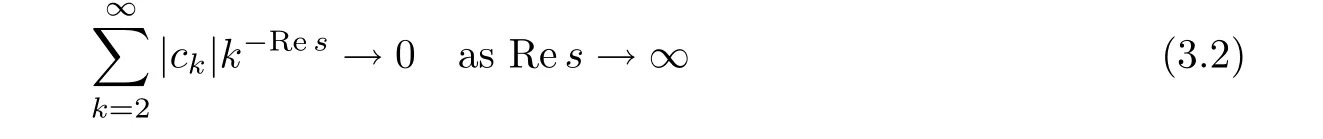
with uniform convergence.In addition,in the case of c0=0,we have Rec1>1/2(see[8],p.319).Hence,in some sufficiently remote half-plane s∈Cθ(θ∈R+),the inequality

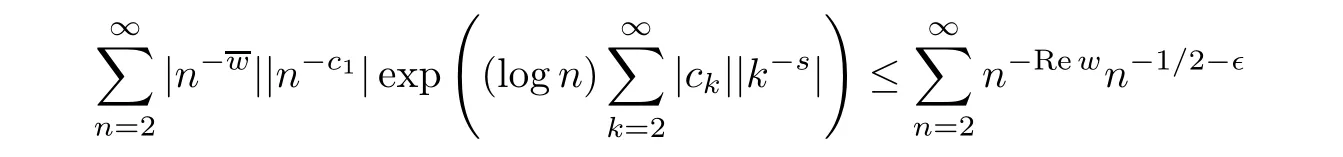
holds with some ǫ>0,and then

Also,the right hand side of(3.1)is

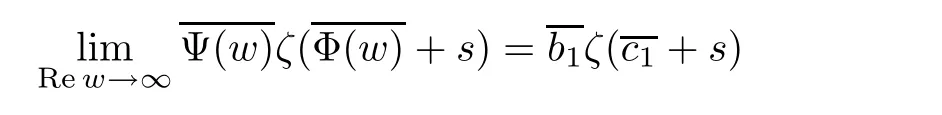
for s in some sufficiently remote half-plane.In fact,it follows from(3.2)that the expressionis uniformly bounded in some half-plane w ∈ Cϑ(ϑ ∈ R+).Then the series ζ(Φ(w)+s)is absolutely convergent in some sufficiently remote half-plane s ∈ Cθ′(θ′∈ R+).Therefore

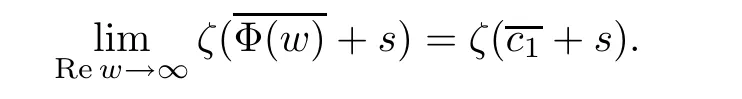
Consequently,Ψ(s)=b1ζ(c1+s).Now let Res→ ∞,then again following from Lemma 2.2,b1=b1.Therefore Ψ(s)=b1ζ(c1+s)with b1∈ R.

Now,(3.1)can be written as

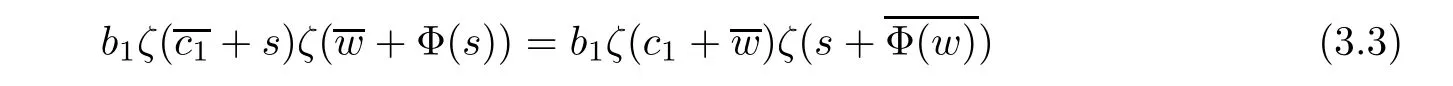
for each s,w∈C1/2.Note that

for some dk∈C,in the half-plane of the absolute convergence of the Dirichlet series obtained by expanding above.We now consider the coefficients of form p−wfor every prime number p of both sides in(3.3).It is easy to see that

Note that ζ(c1+s)6=0 with s ∈ C1/2for Re(s+c1)>1.Then the desired is obtained. ?

The following corollary may be interesting.

Proof Clearly,it suffices to show the sufficiency.To this end,assume that cp=0 for some prime number p.If the weighted composition operator WΨ,Φis Hermitian on H and b16=0,then p−Φ(s)=p−c1by Theorem 3.2.Thus ReΦ(s)=Rec1and for each s∈ C1/2,

with some integer ks.Since Φ is analytic in C1/2,then ImΦ(s)is continuous.Therefore ImΦ(s)=Imc1,which in turn implies that Φ(s)=c1in C1/2. ?

Next,we consider the case c0≥1.

Proof The sufficiency is trivial,so it is needed only to prove the necessity.If WΨ,Φis Hermitian on H,then as in the proof of Theorem 3.2,

for s,w∈C1/2.First,since c0≥1,then it follows from Lemma 2.2 that

in some sufficiently remote half-plane s∈ Cθ(θ∈ R+).Indeed,it is sufficient to notice that the expressionis uniformly bounded in some half-plane,and

Next,it is easy to see that the series ζ(Φ(w)+s)in(3.4)is absolutely convergent in some half-plane w∈Cϑ(ϑ∈R+),due to the fact that the analytic function

for each s∈C1/2.Therefore

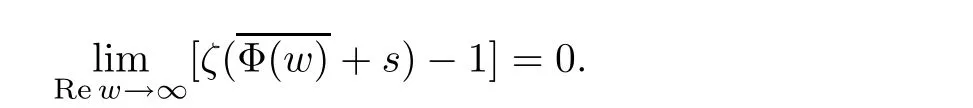
Then letting Rew → ∞ in(3.4)implies that Ψ(s)= Ψ(+∞).Thus b1=b1,and then Ψ is a real-valued constant function on C1/2.If Ψ is nonzero,then WΨ,Φ=TΨCΦis Hermitian on H if and only if CΦis Hermitian on H.In this case,by Lemma 3.1,we have Φ(s)=s+c1with c1≥0.Then the necessity is proved. ?

The following characterizes the Hermitian isometric weighted composition operators.

Theorem 3.5 Let Ψ ∈ H and Φ a c0-symbol.Then the weighted composition operator WΨ,Φis a Hermitian isometry on H if and only if Ψ ≡ 1 or −1 on C1/2,and Φ is the identify function of C1/2.

Proof Clearly,it is needed only to show the necessity.To complete the proof,we first claim that the Hermitian weighted composition operator WΨ,Φon H can never be isometric in case c0=0.In fact,if c0=0 and WΨ,Φis Hermitian on H,then by Theorem 3.2,Ψ(s)=b1ζ(c1+s)with some b1∈ R.Thus for each w ∈ C1/2,we have

If WΨ,Φis an isometry on H,then kWΨ,Φ(Kw)k=kKwk,and thus

for each w ∈ C1/2.But it follows from Lemma 2.1 that there exist η >0 and ǫ>0 such that Φ(C1/2−ǫ)⊂ C1/2+η.Now take a sequence of points wnin C1/2satisfying that wn→ w0with Rew0=1/2,as n→∞.And set Φ(wn)→as n→∞.So Re>1/2+η.Replacing w by wnand letting n→∞in(3.5)yield that the right hand side tends to the infinity,but the left hand side is

because of Rec1>1/2.This is a contradiction,which implies the claim.

Next,assume that c0≥1,due to the Hermitianness of the weighted composition operator WΨ,Φand Theorem 3.4,then Ψ ≡ 0,or Ψ(s) ≡ b1on C1/2with b1a nonzero real constant,and Φ(s)=s+c1with c1≥ 0.Note that Ψ can never be a zero constant function.So in this case,WΨ,Φ(f)(s)=b1f(s+c1)for all f ∈ H.Since WΨ,Φis an isometry on H,

At the end of this section,we characterize the spectra of Hermitian weighted composition operators on H in case c0≥1.

Proof Under the hypothesis,it follows from Theorem 3.4 that either Ψ ≡ 0,or Ψ is a nonzero real-valued constant function on C1/2,and Φ(s)=s+c1with c1≥ 0.It is only needed to consider the case that Ψ(s)≡ b1with b1∈ R{0}.In this case,CΦ:H → H is Hermitian and Φ(s)=s+c1with c1≥ 0.Then WΨ,Φ(f)=b1CΦ(f)for all f ∈ H.Notice that we can obtainand σp(CΦ)={n−c1:n ≥ 1}by the same method as in the proof of Theorem 3.1 in[18].Soby the spectral mapping theorem. ?

4 Fredholmness and Invertibility

Let X be a Banach space,and denote by B(X)the space of all bounded linear operators on X.Recall that an operator T∈B(X)is said to be Fredholm if both the dimension of its kernel and the codimension of its range are finite.This occurs if and only if both KerT and KerT∗are finite dimensional.Equivalently,T is Fredholm if and only if T is invertible modulo compact operators,that is,there is a bounded operator S∈B(X)such that both TS−IXand ST−IXare compact on X,where IXis the identity operator on X.It is well-known that an operator T is Fredholm if and only if its adjoint T∗is Fredholm;see[13]for more details on Fredholm operators.

Lemma 4.1 Let Φ be a c0-symbol.If the weighted composition operator WΨ,Φis Fredholm on H,then Φ(s)=s+iτ with τ∈ R.

Proof We argue by contradiction.If Φ(s)6=s+iτ, τ ∈ R,then by Lemma 2.1,Φ(C1/2−ǫ) ⊂ C1/2+ηfor some ǫ,η >0.To complete the proof,we choose a sequence of complex numbers wnin C1/2such that wn→w0with Rew0=1/2,as n→∞.And then let Φ(wn)→with Re>1/2+η,as n→∞.Also notice that for each w∈C1/2,

where kwis the normalized reproducing kernel at w given by kw:=Kw/kKwk,and

because of Ψ∈H.While

for each w∈C1/2,since kw=Kw/kKwk converges weakly to zero as Rew→1/2 and Ψ∈H,then k(kwn)k→0,as n→∞.

On the other hand,since WΨ,Φis Fredholm,there are operators S and K on H with K compact such that WΨ,ΦS=I−K,where I is the identity operator on H.Hence S∗=I−K∗,and also

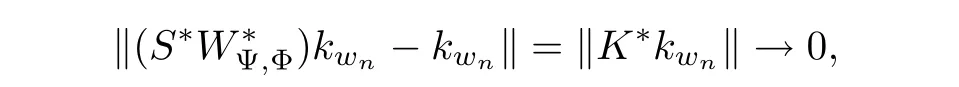
as n→∞.Thus we get k(S∗)kwnk→1 as n→∞.As this is a contradiction,we conclude that Φ(s)=s+iτ with τ∈ R. ?

Now we can characterize the Fredholm weighted composition operators.

Theorem 4.2 Let Φ be a c0-symbol.The weighted composition operator WΨ,Φis Fredholm on H if and only if the multiplication operator TΨis Fredholm and Φ(s)=s+iτ with τ∈R.

Proof We first assume that WΨ,Φis Fredholm on H.Lemma 4.1 asserts that Φ(s)=s+iτ with τ∈ R.Then by Theorem 14 in[1],CΦis invertible on H,and=CΦ−1.Therefore the operator TΨ=WΨ,Φis bounded on H.Furthermore,

and

Thus TΨis Fredholm.

Conversely,suppose that TΨis Fredholm and Φ(s)=s+iτ with τ∈ R.Then CΦis invertible.Since WΨ,Φ=TΨCΦ,KerWΨ,Φ=KerTΨand KerW∗Ψ,Φ=KerT∗Ψ,then the claim follows. ?

Next we consider the invertible weighted composition operators.

Lemma 4.3 Let Φ be a c0-symbol.If the weighted composition operator WΨ,Φis invertible on H,then Φ(s)=s+iτ with τ∈ R,and Ψ is bounded on C+and bounded away from zero on the half-plane C1/2.

Proof Since every invertible linear operator is Fredholm and WΨ,Φis invertible on H,then Φ(s)=s+iτ with τ∈ R by Theorem 4.2.Thus by[1,Theorem 14],CΦis invertible onSo WΨ,ΦCΦ−1is also bounded.Note that for f ∈ H,

Hence WΨ,ΦCΦ−1is the multiplication operator whose multiplier is Ψ.By Theorem 7 in[1],Ψ is in U,which implies that Ψ is bounded on C+.

Moreover,since WΨ,Φis invertible on H,the adjoint W∗Ψ,Φis bounded from below.Then

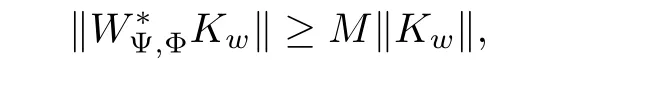
and hence

for all w∈C1/2and some positive constant M.Note that

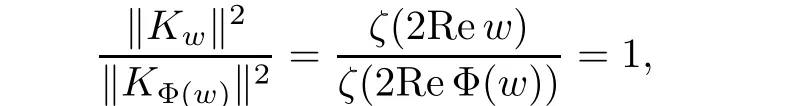
which implies that Ψ is bounded away from zero on the half-plane C1/2. ?

In the next theorem the inverse of weighted composition operators are formulated.

Theorem 4.4 Let Φ be a c0-symbol.The weighted composition operator WΨ,Φis invertible on H if and only if the following statements hold

(1) Φ(s)=s+iτ,τ∈ R.

(2)Ψ is bounded on C+and bounded away from zero on the half-plane C1/2.Moreover,(WΨ,Φ)−1=W1/Ψ◦Φ−1,Φ−1.

Proof The necessity is Lemma 4.3,so it is needed only to show the sufficiency.To this end,assume that Φ(s)=s+iτ(τ∈ R),then CΦis invertible on H andis a bounded operator with Φ−1(s)=s − iτ,τ∈ R.Also assume that Ψ is bounded on C+and bounded away from zero on the half-plane C1/2,then Ψ◦Φ−1is also analytic and bounded away from zero on C1/2.Hence 1/Ψ◦Φ−1is bounded on C1/2.We now claim that 1/Ψ◦Φ−1∈ H.Indeed,by Bohr’s theorem,it suffices to show that 1/Ψ◦Φ−1∈ D.For this,supposethen it is clear to see that b16=0,by the assumption that Ψ is bounded away from zero on C1/2.Note that

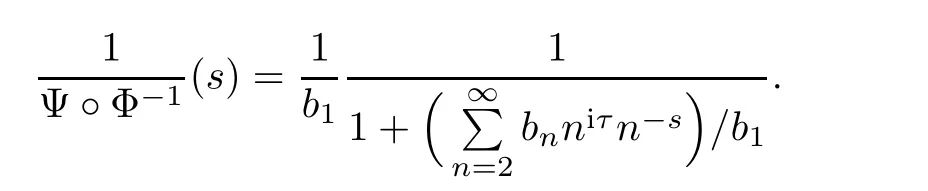
It follows from Lemma 2.2 that there exists a positive constant r<1,such that

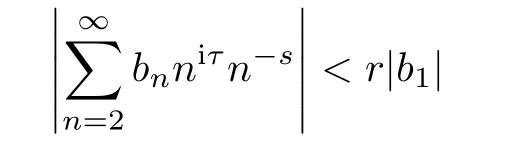
in some possibly remote half-plane Cθ(θ∈R+).So

converges absolutely on Cθ,which implies the desired.

Then T1/Ψ◦Φ−1CΦ−1=W1/Ψ◦Φ−1,Φ−1is a bounded operator on H.Moreover,a computation implies that

for any f∈H,which yields the desired result.?

5 Spectrum

Here,we will also distinguish the cases c0=0 and c06=0.Recall that,if c0=0,then Φ(+∞)6=+∞.In particular,Φ admits a fixed point in C1/2.

Lemma 5.1 Let Φ be a c0-symbol with c0=0.Then the spectrum of the bounded weighted composition operator WΨ,Φon H contains the number Ψ(α)(Φ′(α))jfor any nonnegative integer j,where α is the fixed point of Φ in C1/2.

Proof The proof uses the ideas from Lemmas 2 and 3 in[9]and Theorem 4 in[2].We denote by Kαthe reproducing kernel at α∈C1/2and by K[m]αits m-th derivative.Ifthen

where f(m)(α)is m-th derivative of f at α.Set Km=span{Kα,,···,}.Then we claim that Kmis an invariant subspace ofin H.In fact,for any f∈H,

Now take is the n-th derivative of Ψ ·f(Φ)at α,that is,

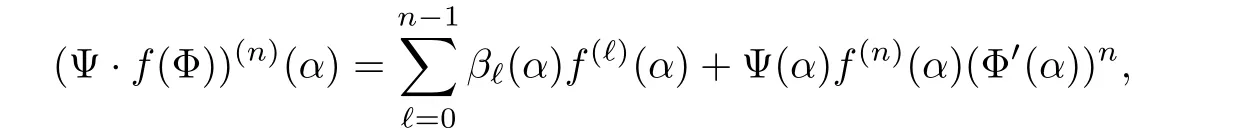
where βℓ(α)∈ C for ℓ=0,1,···,n − 1.So

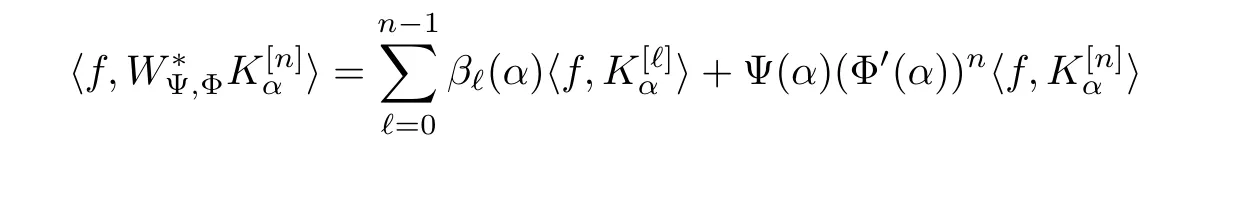
which implies that

Notice that the order of the highest derivative on the right hand side does not exceed n.So the desired result is obtained.

Next,for each m,let Xmbe the restriction ofto Km.Then by the above argument,the matrix Amof the operator Xmwith respect to this basis is upper-triangular,and the elements on the diagonal arefor integers 1 ≤ j ≤ m.

Moreover,it is obvious that the subspace Kmis finite dimensional and therefore is closed.Then Amis a finite-dimensional upper-triangular matrix,whose spectrum consists of the diagonal values.Therefore by Lemma 2.3,the spectrum ofcontains the set

Since m is arbitrary,any number of the form,for any nonnegative integer j,is in the spectrum of the adjoint operatoSo the spectrum of the operator WΨ,Φcontains the numbers of the form Ψ(α)(Φ′(α))jfor any nonnegative integer j,which completes the proof.?

Now we completely describe the spectra of compact weighted composition operators in case c0=0.

Theorem 5.2 Let Φ be a c0-symbol with c0=0.If the weighted composition operator WΨ,Φis compact on H,then

where α is the fixed point of Φ in C1/2.

Proof By Lemma 5.1,it is sufficient to prove that the spectrum of the compact weighted composition operator WΨ,Φis contained in the set

where α is the fixed point of Φ in C1/2.To end the proof,here we continue to use the same notation as in the proof of Lemma 5.1.For each fixed m∈N,let Lmbe the orthogonal complement of Kmin H.Then we can give the block matrix for W∗Ψ,Φ

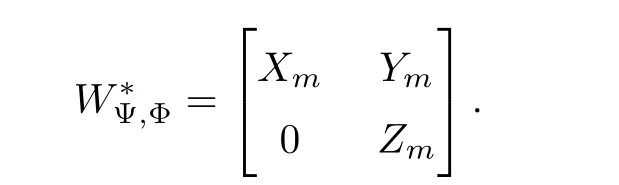
where the first two terms are in Kmand the last is in Lm.In particular,

which contradicts the compactness of

The following two lemmas concern the point spectrum of weighted composition operators in case c06=0.

Proof Assume that the weighted composition operator WΨ,Φis bounded on H.Let f(s)=be an eigenvector of WΨ,Φfor λ,so that

In the above equation,we first take s=+∞.Then we have either λ =b1,or λ 6=b1and a1=0.Next writewith ℓ≥ 2 and aℓ6=0,and consider the coefficient of ℓ−sin Ψ(s)f(Φ(s)).Note that the Dirichlet series of Ψ(s)f(Φ(s))can be obtained by expanding the product in the representation

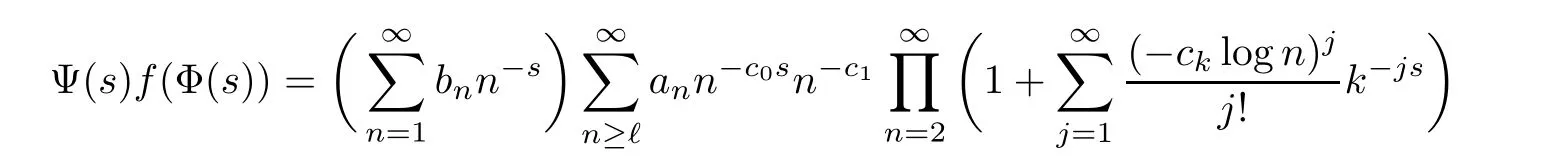
in some(possibly remote)half-plane Cθ′(θ′∈ R+).In particular,if c0>1,there is no term involving ℓ−s,and then σp(WΨ,Φ) ⊂ {b1}.If c0=1,the coefficient of ℓ−sis b1aℓℓ−c1.Hence λaℓ=b1aℓℓ−c1,and λ =b1ℓ−c1. ?

(1){b1}∪{b1n−c1:n ≥ 2}⊂ σ(WΨ,Φ),if c0=1.

(2){b1} ⊂ σ(WΨ,Φ),if c0>1.

Proof(1)For c0=1,let Km=Span{1,2−s,···,m−s}and Lm=Km⊥.Then Lmis invariant under WΨ,Φand we have the block decomposition

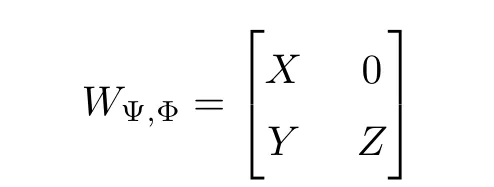
with respect to the decomposition H=Km⊕ Lm,which ensures that σ(X)⊂ σ(WΨ,Φ).Note that

in some(possibly remote)half-plane Cθ(θ ∈ R+).In particular,the matrix of X is lowertriangular and the subspace generated by Kmis finite dimensional,and therefore σ(X)={b1,b12−c1,···,b1m−c1}.By the arbitrariness of m,{b1} ∪ {b1k−c1:k ≥ 2} ⊂ σ(WΨ,Φ).

(2)For c0>1,one can use the similar argument as above to get that{b1} ⊂ σ(WΨ,Φ).?

In the next theorem we summarize the preceding results to characterize the spectrum of the compact weighted composition operator on H.

(1)If c0=0,σ(WΨ,Φ)={0,Ψ(α),Ψ(α)(Φ′(α))1,Ψ(α)(Φ′(α))2,···},where α is the fixed point of Φ in C1/2.

(2)If c0=1,σ(WΨ,Φ)={0,b1}∪ {b1n−c1:n ≥ 2}.

(3)If c0>1,σ(WΨ,Φ)={0,b1}.

At the end of this section,we consider the spectra of the invertible weighted composition operators.

Theorem 5.6 Assume that Φ(s)=s+iτ with τ∈ R and the weighted composition operator WΨ,Φis invertible on H.Then

where kΨkinfis the infimum of Ψ on C1/2.

which implies that kf ◦ Φnk=kfk.Also(WΨ,Φ)n(f)(s)= Ψ(n)(s)f(Φn(s)),then

which implies that k(WΨ,Φ)nk ≤ kΨkn∞.Therefore

Similarly,we can get

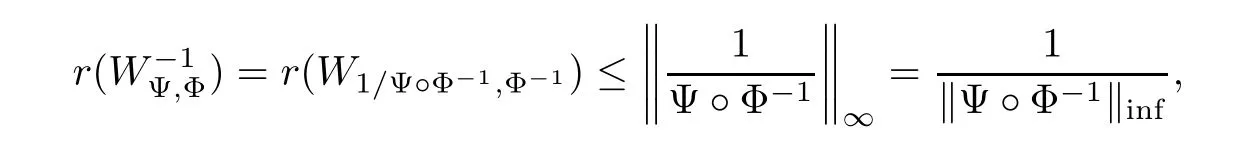
where kΨ ◦ Φ−1kinf=inf{|Ψ(Φ−1)(s)|:s ∈ C1/2}.It is obvious that kΨ ◦ Φ−1kinf=kΨkinf.Thereforefor any λ ∈ σ(WΨ,Φ),then|λ|≥kΨkinf.So

Recall that a well-known fact that,for a bounded analytic function F in Cθ,the associated function

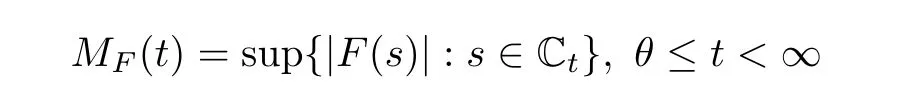
is decreasing and logarithmically convex(see[15,Theorem 12.8]).We apply the fact above to the function Ψ,then which completes the proof.