GENERALIZED DISCRETE Q-HERMITE I POLYNOMIALS AND Q-DEFORMED OSCILLATOR∗
2018-09-08KamelMEZLINI
Kamel MEZLINI
High Institute of Applied Sciences and Technologies of Mateur,University of Carthage,Tunisia
E-mail:kamel.mezlini@lamsin.rnu.tn;kamel.mezlini@yahoo.fr
Néji BETTAIBI
Department of Mathematics,College of Science,Qassim University,KSA
E-mail:neji.bettaibi@ipein.rnu.tn
Abstract In this paper,we present an explicit realization of q-deformed Calogero-Vasiliev algebra whose generators are first-order q-difference operators related to the generalized discrete q-Hermite I polynomials recently introduced in[14].Furthermore,we construct the wave functions and we determine the q-coherent states.
Key words basic orthogonal polynomials;quantum algebra;coherent states
1 Introduction
The q-deformed harmonic oscillator algebras[11,12,16,17]were intensively studied in recent years due to their crucial role in diverse areas of mathematic and physics.The basic interest in q-deformed algebras resides in the generalization of the fundamental symmetry concept of classical Lie algebras.
Many algebraic constructions were proposed to describe various generalization of the quantum harmonic oscillator in the literature.The difficulty for most of them is to realize an explicit form of the associated Hamiltonian eigenfunctions.It is well known that the Hermite polynomials are connected to the realization of the classical harmonic oscillator algebra.It is natural then,that generalizations of quantum harmonic oscillator lead to generalizations of the Hermite polynomials.An explicit realization of the q-harmonic oscillator was explored by many authors see for example Atakishiev[2,3],Borzov[6],also Kulish and Damaskinsky[16],where the eigenfunctions of the corresponding Hamiltonian are given explicitly in terms of the q-deformed Hermite polynomials.The generators of the corresponding algebra are realized in terms of first-order difference operators.
In particular,as pointed out by Macfarlane in[17,18],the Calogero-Vasiliev oscillator generalizes the parabose oscillator and its q-deformation describes the q-analogue of the parabose oscillator[12].In one dimensional case,Rosenblum in[21]studied the generalized Hermite polynomials associated with the Dunkl operator and used them to construct the eigenfunctions of the parabose oscillator Hamiltonian.This oscillator,as it was shown in[18],is linked to two-particle Calogero model[7].
The purpose of this paper is to explore the generalized discrete q-Hermite I polynomials hn,α(x;q),recently introduced in[14]to construct the Hamiltonian eigenfunctions for the qdeformed Calogero-Vasiliev oscillator.This allows to find an explicit form of the generators of the corresponding algebra in terms of q-difference operators.
This paper is organized as follows:in Section 2,we recall some notations and useful results from[14]about the generalized discrete q-Hermite I polynomials hn,α(x;q).In Section 3,we review briefly the Fock space description of the Calogero-Vasilievoscillator and its q-deformation as developed by Macfarlane in[17,18].In Section 4,we introduce an explicit form of the eigenfunctions of the q-deformed Calogero-Vasiliev oscillator Hamiltonian.This directly leads to the dynamical symmetry algebra(1,1),whose generators are explicitly constructed in terms of the q-difference operators,we construct the family of coherent states of this oscillator.Finally,we investigate the limiting case of the q-deformed Calogero-Vasiliev oscillator.
2 Notations and Preliminary
For the convenience of the reader,we provide in this section a summary of the mathematical notations and definitions used in this paper.We refer to the general reference[13]and[14]for the definitions and notations.Throughout this paper,we assume that 0 The q-number and the q-factorial are defined as follows: We shall also use an alternative definitions of q-number and the q-factorial,which are symmetric under q↔ q−1, It is easy to see that for all x∈C,have the property and the relation The generalized q-integers and the generalized q-factorials are defined by For complex number a,the q-shifted factorials are defined by For α ∈ R,the generalized q-shifted factorials(q;q)n,αare defined by We may express the generalized q-factorials as where Γq(z)is the q-Gamma function given by(see[10,13]) and tends to Γ(z)when q tends to 1−.In particular,we have the limits where γµis the Rosenblum’s generalized factorial(see[21]). Remark 2.1 If α = −12,then we get(q;q)n,α=(q;q)nand n!q,α=n!q. The two Euler’s q-analogues of the exponential function are given by(see[13]) For z∈C,the generalized q-exponential functions are defined by(see[14])and[x]denoting the integer part of x ∈ R.Note that(z)is the q-Dunkl kernel defined in[4]. A particular case,where α =,and by Remark 2.1 it follows that Eq,α(z)=Eq(z)and eq,α(z)=eq(z). The Jackson’s q-derivative Dq(see[9,13,15])is defined by The generalized backward and forward q-derivative operators Dq,αandare defined as(see[14]) The generalized q-derivatives operators are given by where feand foare respectively the even and the odd parts of f defined by We can rewrite the q-Dunkl operator introduced in[4]by means of the generalized q-derivative operators as It is noteworthy that for a differentiable function f,we have where Λνis the classical Dunkl operator defined by We shall need the Jackson q-integral defined by(see[9,13,15]) The generalized q-exponential function(x)gives rise to a q-integral transform,called the q-Dunkl transform on the real line,which was introduced in[4]as where and The Calogero-Vasiliev oscillator algebra[17,18](also called the deformed Heisenberg algebra with reflection[8])is generated by the operators{I,a,a+,N,K}subject to the Hermiticity conditions and it satisfies the relations where[A,B]=AB − BA.The operators a−,a+and N generalize the annihilation,creation and number operators related to the classical harmonic oscillator. This oscillator,as it has been shown by Macfarlane in[17],also describes a parabose oscillator of order p=2ν+1.In particular,is linked to two-particle Calogero model[18]and Bose-like oscillator[21].This algebra has a basic one-dimensional explicit realization in terms of difference-differential operators where I is the identity mapping and Λνis the Dunkl operator defined by(2.21).The Hamiltonian is expressed as where{A,B}=AB+BA.The eigenvalues of H are n++ν and corresponding eigenvectors(x),which are the generalized Hermite functions introduced by Rosenblum in[21]as where γνthe generalized factorial on which the conjugation relations(3.1)are satisfied.Let Sνbe the space spanned by the generalized Hermite functions{φνn(x)}∞n=0.The operators Aν,A+νand N act on Sνas follows The number operator N is given explicitly in terms of the creation and annihilation operators by K is realized in terms of the N operator K=(−1)N.Obviously,the operators Aν,A+ν,N and K satisfy the commutation relations(3.2)and(3.3)on Sν. It is well known that in one dimension the two-particle Calogero system realizes an irreducible representations of the Lie algebra su(1,1)[19].Then one can easily verify that the operators satisfy the commutation relations Thus K0,K+and K−are the generators of Lie algebra su(1,1).The representations are characterized by eigenvalues of the Casimir operator given by which commutes with K0,K±.It follows from(3.6)that C takes the value throughout the even and odd subspaces of Sν.Thus S±νcarry out unitary irreducible representations of su(1,1)with distinct eigenvalues of the Casimir operator C. The q-deformed Calogero-Vasiliev oscillator algebra is defined as the associative unital algebra generated by the operators{b,b+,N}which satisfy the relations where[x]qis the q-number defined in(2.1)and K=(−1)N. The Fock representation of this q-oscillator algebra is constructed on a Hilbert space H with an orthonormal basis{en}∞n=0.The operators b,b+,and N act on the subspace Sqνspanned by the basis vectors enaccording to the formulas(see[17,18,22]) It follows from(3.9)that we have the following equalities The operators b,b+and N directly lead to the realisation of the quantum algebra suq(1,1)with the generators(see[16–18]) They satisfy the commutation relations and the conjugation relations The Casimir operator C,which by definition commutes with the generators K±and K0is The action of the operator C on the vectors enis given by the formulas In the space Sqνthe Casimir operator C has two eigenvalueswith eigenvectors in the subspacesformed by the even and odd basis vectors en,respectively.Thus Sqνsplits into the direct sum of two suq(1,1)-irreducible subspacesand In particular Macfarlane in[18]explored the links between the q-Deformed Calogero-Vasiliev Oscillator and the q-analogue of the parabose oscillator of order p=2ν+1 studied in[12]. In this section we discuss an explicit realization of one-dimensional q-deformed Calogero-Vasiliev oscillator algebra.We give an explicit expression of the representation operators b,b+and N defined in the previous subsection in terms of q-difference operators.It is known that such representation can be realized on a Hilbert space,on which all these operators are supposed to be well defined and the conjugation relations in(3.7)hold.For this purpose we take as Hilbert space,the space(X)equipped with the scalar product The generalized discrete q-Hermite I polynomials{hn,α(x;q)}∞n=0are defined by(see[14]) They have the following properties. •Generating function •Inversion formula •Forward shift operator or equivalently •Backward shift operator or equivalently •Orthogonality relation where We now construct a convenient orthonormal basis of(X)consisting of the(q,α)-deformed Hermite functions defined by where hn,α(x;q)and dn,αare given by(4.1)and(4.9),respectively. Proof The(discrete)orthogonality relation(4.8)for hn,α(x;q)can be written as By using the inverse formula(4.3),we obtain The Plancherel theorem implies that f=0. We denote by δqthe q-dilatation operator in the variable x,defined by δqf(x)=f(qx),and the operator of multiplication by a function g will be denoted also by g. Let Sqαbe the finite linear span of(q,α)-deformed Hermite functions(x;q).From the forward and backward shift operators(4.5)and(4.7),we define the operators A and A+on Sqαin a 2×2 matrix form by where feand foare respectively the even and the odd parts of f ∈ Sqα. The reader may verify that these operators are indeed mutually adjoint in the Hilbert space(X). The action of the operators A and A+on the basisleads to the explicit results. Proposition 4.2 where JnKq,αis defined by(2.3). Proof (4.13)is an emmediate consequence of definitions(4.10).(4.14)and(4.14)follow from the forward and backward shift operators(4.5)and(4.7)and from the fact that From(4.14)and(4.15),one deduces that The number operator N is defined in this case by the relations Using the fact that we obtain Formulas(4.18)can be inverted to determine an explicit expression of the operator N as follows From(4.16),(4.17)and(4.19),we obtain Now,we shall construct explicitly the generators b and b+of the q12-deformed Calogero-Vasiliev algebra defined in the previous subsection by means of the operators A,A+and N in the following way One easily verifies that the actions of operators b and b+on the basisare given by Using relation(2.2),then the expressions in(4.20)can be written as From(4.21),the basis vectors(x;q)may also be expressed in terms of the operator b+and(x;q)as follows where[n]!q,αis the generalized q-factorial given by(2.4). From the above facts,we may check that equation(3.7)holds and We deduce from(4.22)that the operators b and b+satisfy the relations This leads to an explicit expressions for the generators{b,b+,N}of the q12-deformed Calogero-Vasiliev oscillator algebra.The corresponding Hamiltonian is defined from b and b+according to Thus,we recover in the limit q→1 the eigenvalues of the Hamiltonian of the Calogero-Vasiliev oscillator. In the same manner as in the case of su(1,1),by virtue of the results of the previous subsection,we construct an explicit realization of the operators B−,B+and B0generators of the quantum algebra suq12(1,1)in terms of the oscillatorial operators b,b+and N by setting From(4.21),we derive the actions of these operators on the basis It follows that Using the following identity(see[5]p.58) with x=2n+2,y= −2n−2α,z=2 and with x=2n+2,y= −2n−2α −2,z=2,respectively,we obtain from which follows the commutation relations and the conjugation relations We conclude an explicit realization of generators B0,B−and B+of the quantum algebra To analyze irreducible representations ofalgebra,we need the invariant Casimir operator C,which in this case has the form From(4.25)and(4.26),we obtain the action of this operator on the basis Then,the Casimir operator C has two eigenvaluesin the subspacesformed by the even and odd basis vectors{(x;q),respectively.Thus Sqαsplits into the direct sum of two suq12(1,1)-irreducible subspacesand In particular Macfarlane in[18]showed that this oscillator realises the q-deformed parabose oscillator of order p=2ν+1 studied in[12]. Hence we derive an explicit realizations of the annihilation and creation operators of qdeformed parabose oscillator in terms of q-difference operators. The normalised q-coherent state ϕζ(x;q)related to the q-deformed Calogero-Vasiliev oscillator is defined as the eigenfunction of the annihilation operator a with eigenvalue ζ∈C, Theorem 4.1 The q-coherent states are of the form where cαis given in(4.9)and Proof By expressing ϕζ(x;q)in terms of the wave functions(x;q), From the eigenvalue equations(4.13)and(4.14),we can write Replace ϕζ(x;q)by series(4.31)in(4.28)and equate the coefficient of(x;q)on both sides to get By iterating the last relation,we get since f0,α(q)=C0=C0(ζ),the relations which inserted into expansion(4.31),give Now,for ζ,ζ′∈ C,we have the scalar product But,the orthogonality relation(4.8)and definition(4.30)imply that The normalized condition requires to choose So,we can write From definitions(4.10)and(4.9),we obtain By the generating function(4.2)for the polynomials hn,α(x;q)we get the explicit form of the normalized q-coherent state(4.29). Lemma 4.1 ProofWe have We have the limit(see[1],Corollary 10.3.4) In the limit as q→1−the q-Calogero-Vasiliev oscillator reduces to the Calogero oscillator.To show this,one first easily verifies that where∆α,qis defined by(2.17).One rescaleswe get Using limits(4.34),(4.35)and(2.20),we find that By definition of the Rosenblum’s Hermite function φµn(3.5)and property of the Dunkl operator Λα,we have where I is identity map.In the same way,we can write where∆α,qis the operator(2.18).Hence we get By(4.34),(4.35)and(2.20),we obtain Note that if we replace α +by ν we obtain the annihilation and creation operators of onedimensional two-particle Calogero oscillator given by(3.4).2.1 The q-Numbers and the q-Factorials
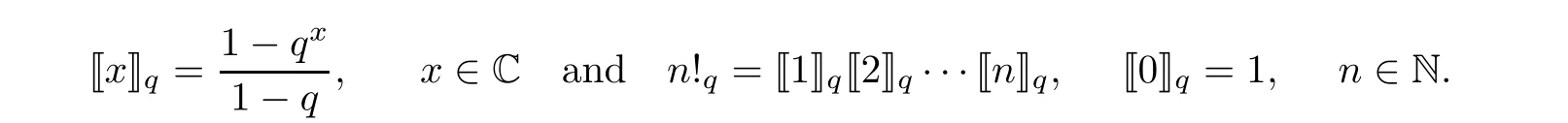







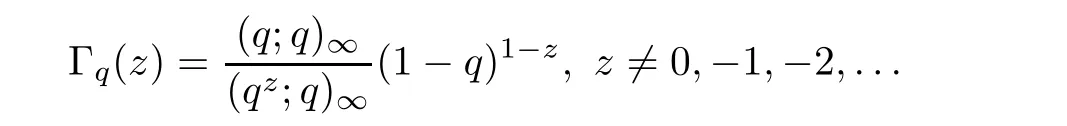

2.2 The Generalized q-Exponential Functions
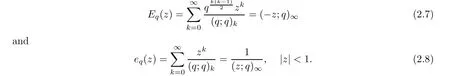
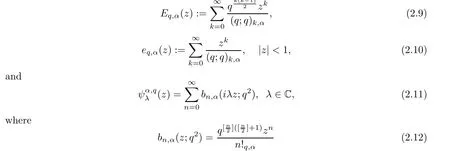
2.3 The Generalized q-Derivatives

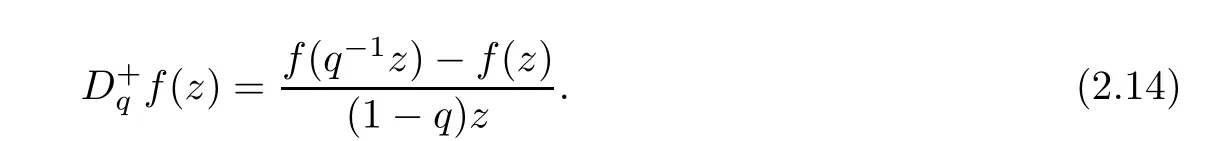

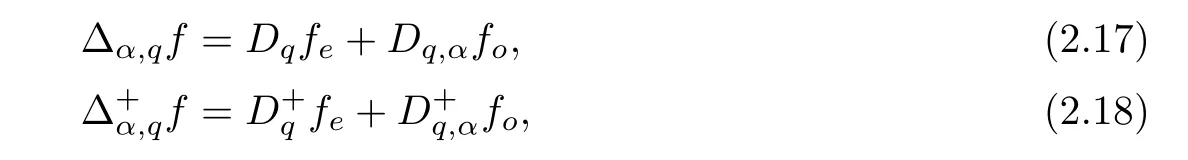
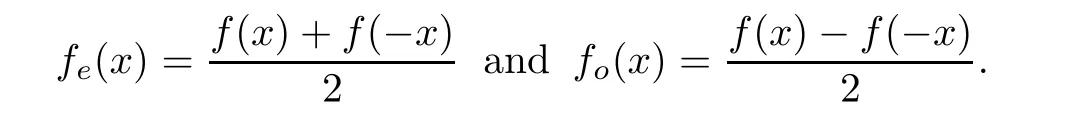



2.4 The q-Dunkl Transform




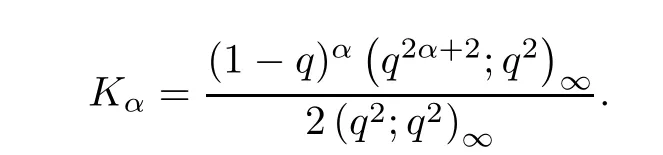
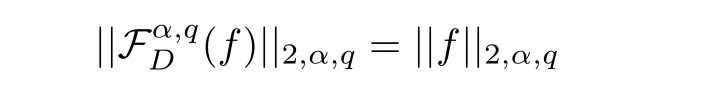
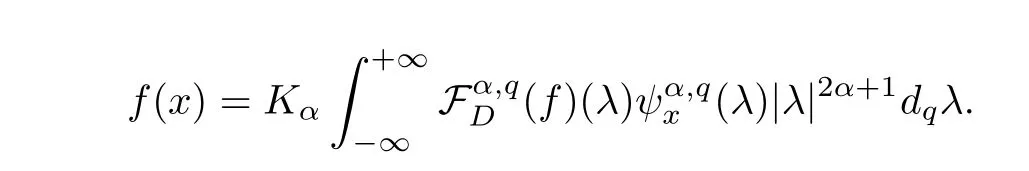
3 The Calogero-Vasiliev Oscillator and q-Deformation
3.1 The Calogero-Vasiliev Oscillator


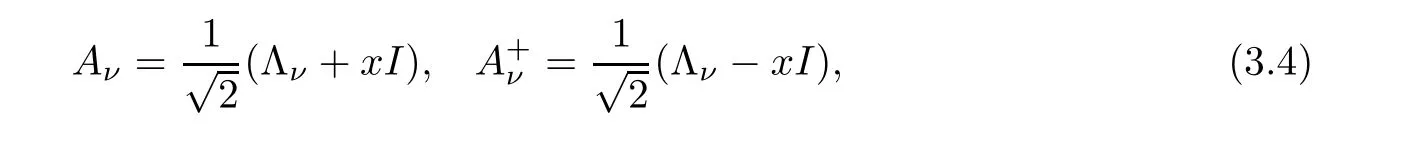





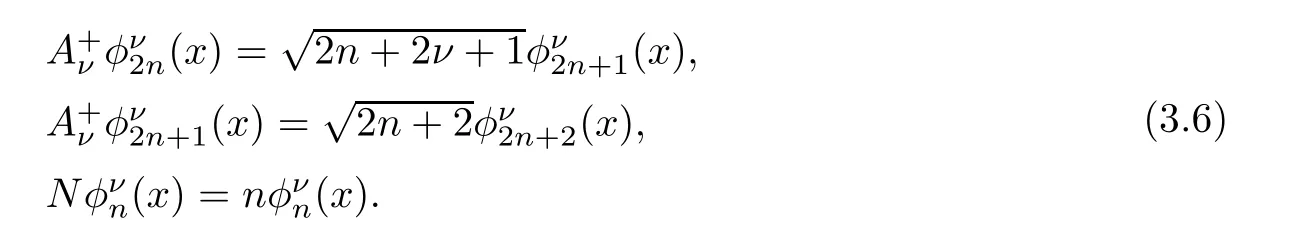



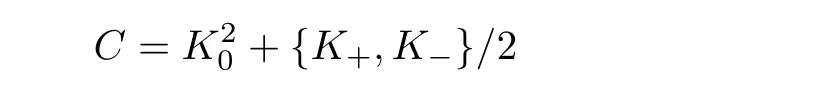
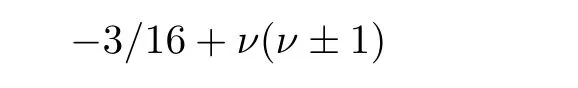
3.2 The q-Deformed Calogero-Vasiliev Oscillator







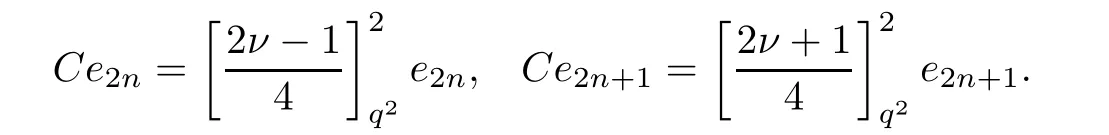
4 Realization of the q-Deformed Calogero-Vasiliev Oscillator

4.1 The Generalized Discrete q-Hermite I Polynomials





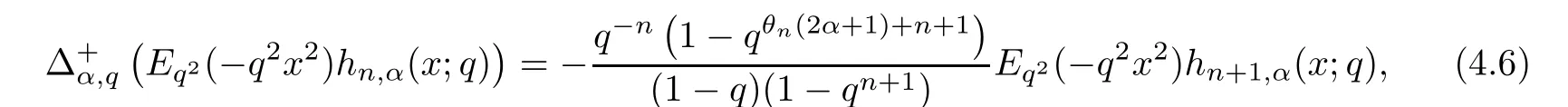


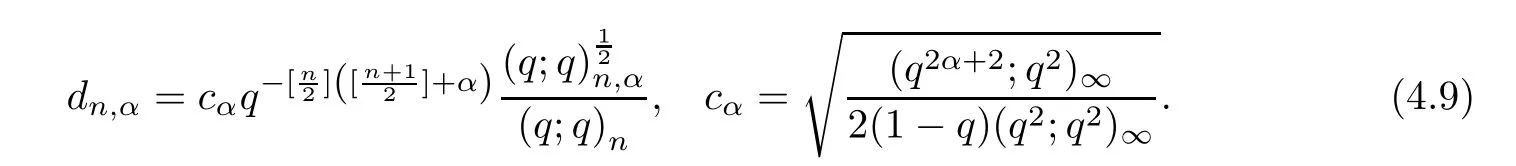
4.2 The(q,α)-Deformed Hermite Functions


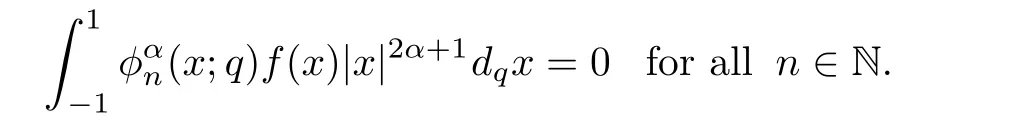
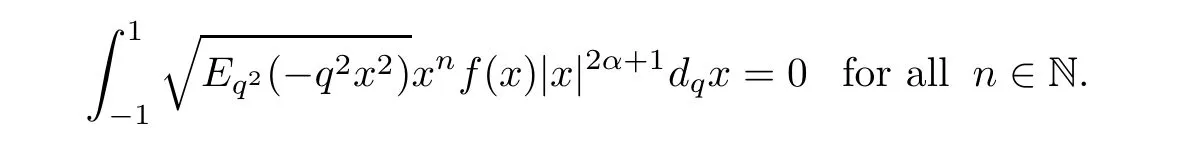


4.3 The-Deformed Calogero-Vasiliev Algebra



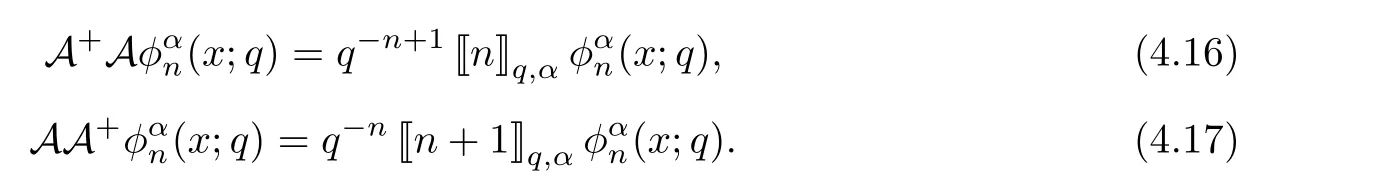

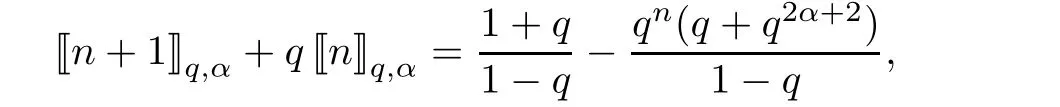
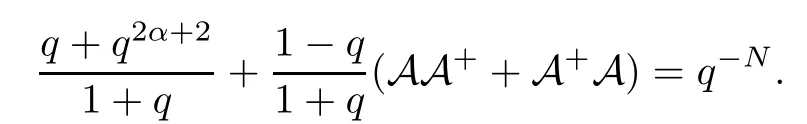



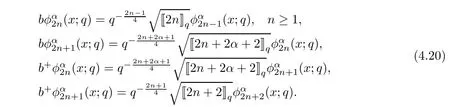

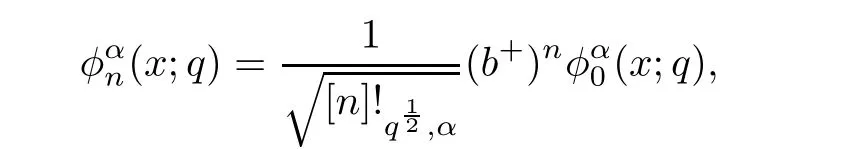




4.4 An Explicit Realization of the Quantum Algebra(1,1)

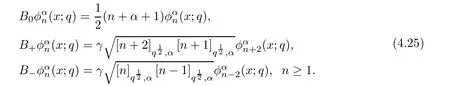









4.5 The q-Coherent States



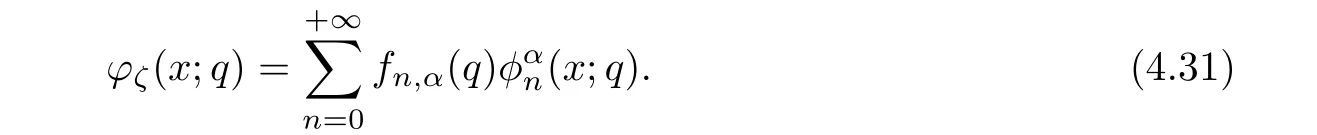



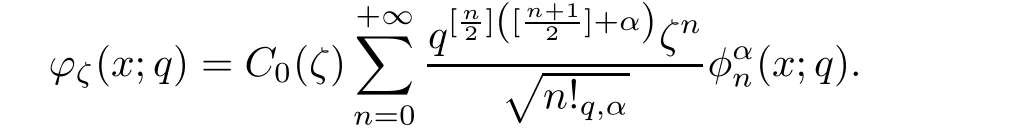

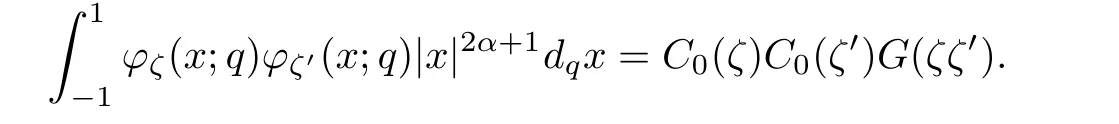
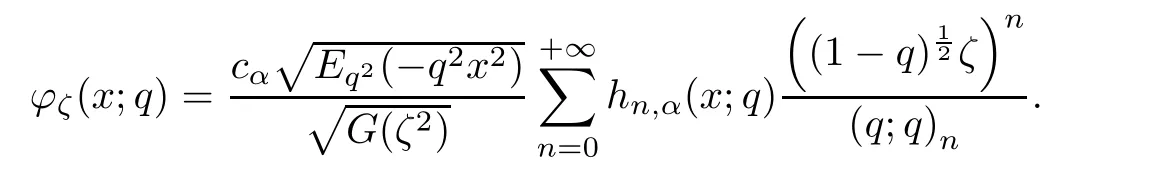
4.6 Limit of the Calogero Oscillator
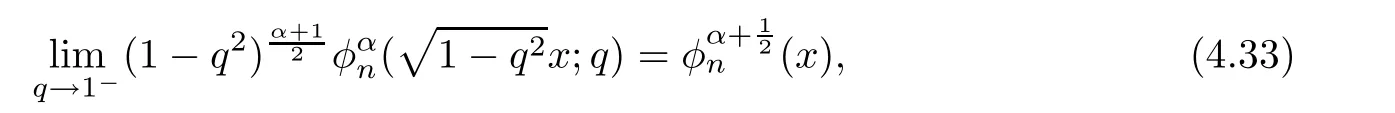
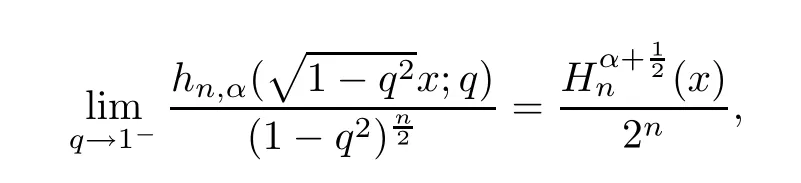









杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- PRODUCTS OF WEIGHTED COMPOSITION AND DIFFERENTIATION OPERATORS INTO WEIGHTED ZYGMUND AND BLOCH SPACES∗
- A NOTE ON THE UNIQUENESS AND THE NON-DEGENERACY OF POSITIVE RADIAL SOLUTIONS FOR SEMILINEAR ELLIPTIC PROBLEMS AND ITS APPLICATION∗
- SOLUTIONS TO THE SYSTEM OF OPERATOR EQUATIONS AXB=C=BXA∗
- BURKHOLDER-GUNDY-DAVIS INEQUALITY IN MARTINGALE HARDY SPACES WITH VARIABLE EXPONENT∗
- CHAIN CONDITIONS FOR C∗-ALGEBRAS COMING FROM HILBERT C∗-MODULES∗
- SINGULAR LIMIT SOLUTIONS FOR 2-DIMENSIONAL ELLIPTIC SYSTEM WITH SUB-QUADRTATIC CONVECTION TERM∗
