PULLBACK EXPONENTIAL ATTRACTORS FOR THE NON-AUTONOMOUS MICROPOLAR FLUID FLOWS∗
2018-09-08孙文龙,黎野平
Abstract This paper investigates the pullback asymptotic behaviors for the non-autonomous micropolar fluid flows in 2D bounded domains.We use the energy method,combining with some important properties of the generated processes,to prove the existence of pullback exponential attractors and global pullback attractors and show that they both with finite fractal dimension.Further,we give the relationship between global pullback attractors and pullback exponential attractors.
Key words micropolar fluid flow;pullback exponential attractor;global pullback attractor;
1 Introduction
In this paper,we investigate the following non-autonomous micropolar fluid equations
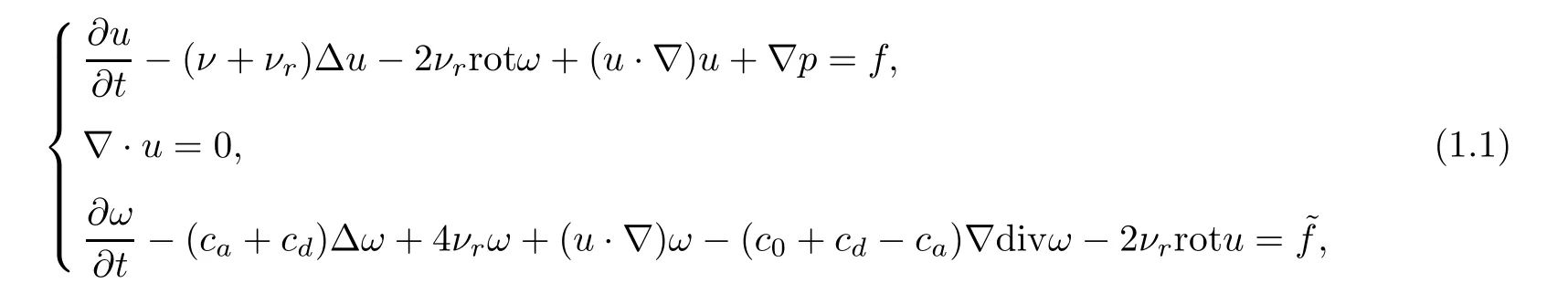
where u=(u1,u2,u3)is the velocity,ω =(ω1,ω2,ω3)is the microrotation field interpreted as the angular velocity field of rotation of particles,p represents the pressure,f=(f1,f2,f3)andare the external force and moments,respectively.The positive parameters ν,νr,c0,ca,cdrepresent the viscosity coefficients.Indeed, ν represents the usual Newtonian viscosity and νris called the microrotation viscosity.System(1.1)was introduced in the pioneer work of Eringen[11]in 1966,which can describe a class of non-Newtonian fluid motions with micro-rotational effects and inertial force involved.This model took an important role in the fields of applied and computational mathematics,and we can see more details in[11,16]etc.Note that when the gyration is neglected,the micropolar fluid flows reduce to the Navier-Stokes flows.
Due to the wide applications in the real world,there is a large literature on the mathematical theory of the micropolar fluid equations(1.1).The existence and uniqueness of solutions for the micropolar fluids was investigated in[12–14,16,17].At the same time,lots of works were devoted to the long time behavior of solutions for the micropolar fluids.More precisely,Chen,Chen and Dong proved the existence of H2-compact global attractors in a bound domain and the existence of uniform attractors in non-smooth domains in[2]and[4],respectively.Lukaszewicz[17]verified the estimates of Hausdor ffand fractal dimension of the L2-global attractor.Later,L ukaszewicz and Tarasin´ska[20]proved the existence of H1-pullback attractor for non-autonomous micropolar fluid equation in a bounded domain.As for the long time behavior of solutions for the micropolar fluid flows on unbounded domains.Dong and Chen[6]discussed the existence and regularity of the global attractors.Later,they[7]obtained the L2time decay rate for global solutions of the 2D micropolar equations via the Fourier splitting method.Chen and Price[3]obtained the L2time decay rate for small solutions of the 3D micropolar equations via Kato’s method.There are also some efforts are focused on the 2D micropolar equations with partial dissipation.Dong and Zhang[8]examined the micro-rotation viscosity,namely ca+cd=0.The global regularity problem for this partial dissipation case is not trivial due to the presence of the term∇×ω in the velocity equation.They overcame the difficulty by making full use of the quantity∇×u−ω,which obeys a transportdiffusion equation.When the parameters ν =0 and νr6=ca+cd,the global well-posedness of the micropolar fluid equations were obtained in the frame work of Besov spaces in[27].More recently,Dong,Li and Wu[10]studied the global regularity and large time behavior of solutions to the 2D micropolar equations with only angular viscosity dissipation,in which they established the well-posedness of the solutions by fully exploiting the structure of the system and controlling the vorticity via the evolution equation of a combined quantity of the vorticity and the micro-rotation angular velocity,and they obtained suitable decay rates of the solution by combining diagonalization process with the uniformly bounded estimates for the first derivatives of the solutions.For more theories about the micropolar fluid flows and other dynamical systems,one can see[5,9,18,19,22–26,28,29,31,32].So far,to our knowledge,there are no results about pullback exponential attractors of the micropolar fluid equations(1.1)in 2D bounded domains.Here,we will partly give a positive answer for this important problem.
In this paper,we consider a two-dimensional micropolar fluid model in a 2D smooth bounded domains Ω⊆R2.More precisely,we set a cross section x3=constant of the threedimensional domain Ω×R when the external fields and the flow itself do not depend on the x3coordinate.Then,we assume that the velocity component u3in the x3direction is zero and the axes of rotation of particles are parallel to the x3axis.In this case,the form of u,ω,f,f are that
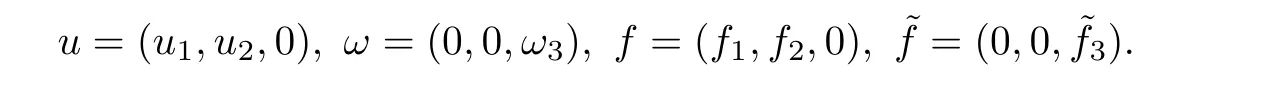
Hence,equations(1.1)can be reduced to the following two-dimensional non-autonomous dy-namical system
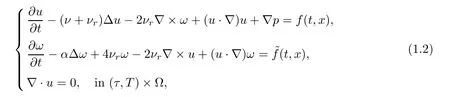
where α:=ca+cd,x:=(x1,x2)∈Ω⊆R2,u:=(u1,u2),f:=(f1,f2),ω andf are scalar functions,

We also give the following initial boundary conditions

Further,introducing the following three operators

we can represent(1.2)–(1.4)into the following abstract form

The purpose of this work is concerned on proving the existence of the pullback exponential attractors being a family of compact and positively invariant sets with finite fractal dimension which pullback attract bounded subsets of the phase space at a uniform exponential rate for the non-autonomous incompressible micropolar fluid flows.In order to state our main results,we first give the following assumption of F in(1.5).
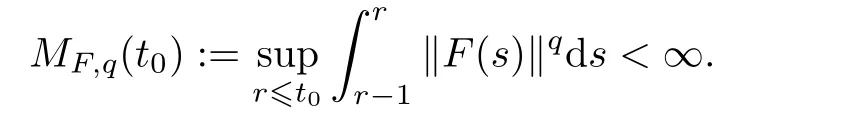
Now we state our main results in the following theorem.
Theorem 1.1 Suppose(H1)holds,then the process UF(t,τ)t>τdefined by(2.13)has a pullback exponential attractorcM={MUF(t):t∈R}with finite fractal dimension.
As a consequence of Theorem 1.1,we also have the following results.
Theorem 1.2 Suppose(H1)holds,then the process UF(t,τ)t>τhas a global pullback attractor={AUF(t):t∈R}with finite fractal dimension.Furthermore,

The outline of the proofs for Theorems 1.1 and 1.2 is as follows.First,we recall the definition of weak solutions for(1.5).Then we derive the estimates of the weak solutions by energy methods.Finally,using the arguments of[21]and some important properties of the generated processes,we prove the existence of pullback exponential attractors and global pullback attractors,and show that they both with finite fractal dimension.Further,we also give the relationship between global pullback attractors and pullback exponential attractors.
Remark 1.3 Compared with the Navier-Stokes equations(w=0,νr=0)in[21],we emphasize that the micropolar fluid flows consist the angular velocity field ω of the micropolar particles,which leads to a different nonlinear term B(u,w)and an additional term N(u)in the abstract equation(see(1.5)).Due to these differences,more delicate estimates and analysis for the solutions are required in our study.
Throughout this paper,we denote the usual Lebesgue space and Sobolev space by Lp(Ω)and Wm,p(Ω)endowed with norms k ·kpand k ·km,p,respectively.
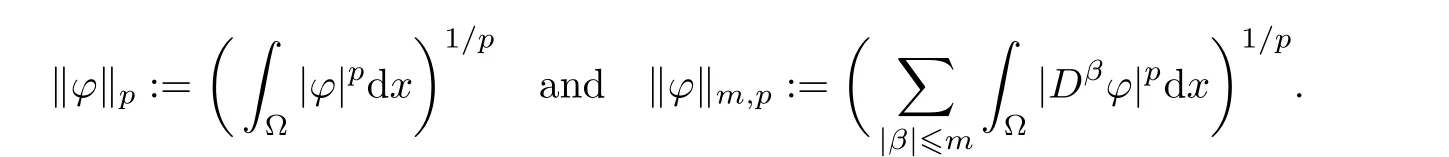
Especially,we denote Hm(Ω):=Wm,2(Ω)and(Ω)the closure of{ϕ ∈(Ω)}with respect to H1(Ω)norm.

(·,·)− the inner product in L2(Ω),H orbH,h·,·i− the dual pairing between V and V∗or between bV andbV∗.Throughout this article,we simplify the notations k·k2,k·kHand k·kbHby the same notation k·k if there is no confusion.Furthermore,we denote
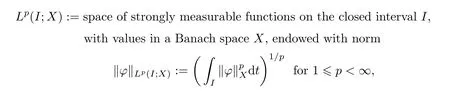

The rest of the paper is organized as follows.In Section 2,we make some necessary preliminaries.That is,we introduce several important definitions and recall some known results of non-autonomous micropolar fluid flows.Section 3 is devoted to investigating some useful estimates of the solutions of the micropolar fluid flows.Finally,we give the proof of Theorems 1.1 and 1.2 by the estimates of the solutions and the properties of the generated process in Section 4.
2 Preliminaries
In this section,we make some necessary preliminaries.That is,we will give some definitions and recall some known results about the non-autonomous micropolar fluid model.To begin with,we list some useful estimates with respect to the operators A,B(·,·)and N(·)as follows.
Lemma 2.1(see[17,18,28,30]) (1)There are two positive constants c1and c2such that
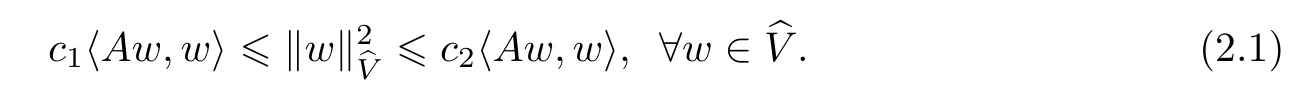
In addition,for any w∈D(A),there holds
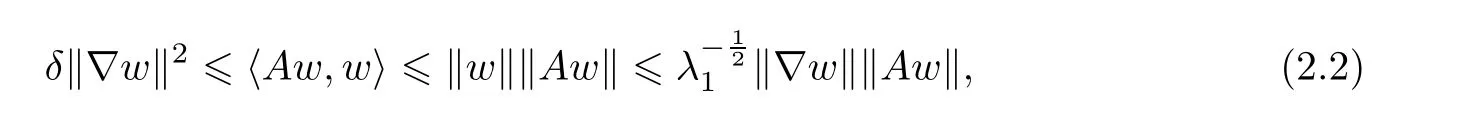
where δ=min{ν + νr,α}and λ1is the constant from(3.1).
(2)There exists a positive constant λ which depends only on Ω,such that for any(u,w,ϕ) ∈V×bV×bV,there holds

Furthermore,for(u,w,ϕ)∈V ×D(A)×and(u,w,ϕ)∈ V ×D(A)×D(A),then the following inequalities hold,respectively,
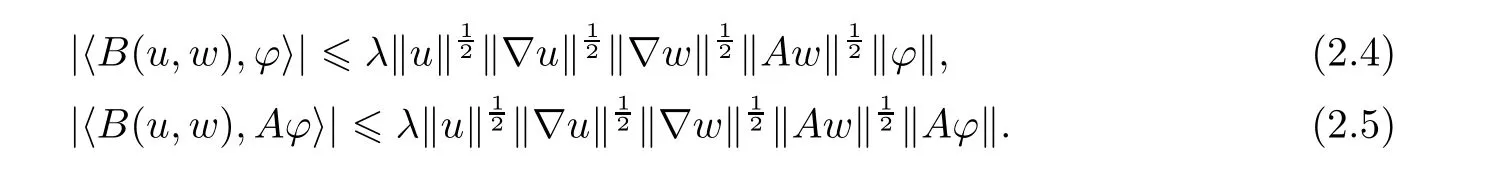
(3)There exists a positive constant c(νr)such that

where δ1:=min{ν,α}.Moreover,for any w ∈ D(A),there holds
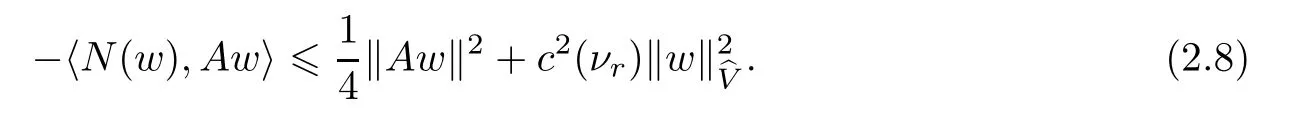
Based on Lemma 2.1,we immediately have
Lemma 2.2 (1)The operator A is a linear continuous operator both fromto∗and fromto,and so is for the operator N(·)fromto
(2)The operator B(·,·)is continuous from V ×to.Moreover,for any u ∈ V,w ∈ bV,there holds
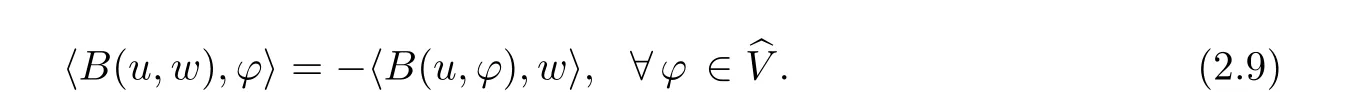
Proof (1)The continuity of the operators A and N(·)follows directly from(2.1)–(2.2)and(2.6),respectively.The linearity of the operator A is evident.So we only need check the linearity of the operator N(·).Indeed,by the definitions of∇ × u(t),∇ × ω(t)and N(·),for anywe see that

(2)The continuity of the operators B(·,·)follows directly form(2.3).We only need to verify(2.9).In fact,for any u∈V,w∈bV,we have

Hence(2.9)is valid as a consequence of(2.10).This completes the proof. ?
Moreover,we give the definition and existence result of weak solutions for(1.5).
Definition 2.3(see[17,28]) For any T> τ,τ∈R,function w is called a weak solution of(1.5)if,w=(u,ω)∈ L2(τ,T;)∩ L∞(τ,T;satisfies
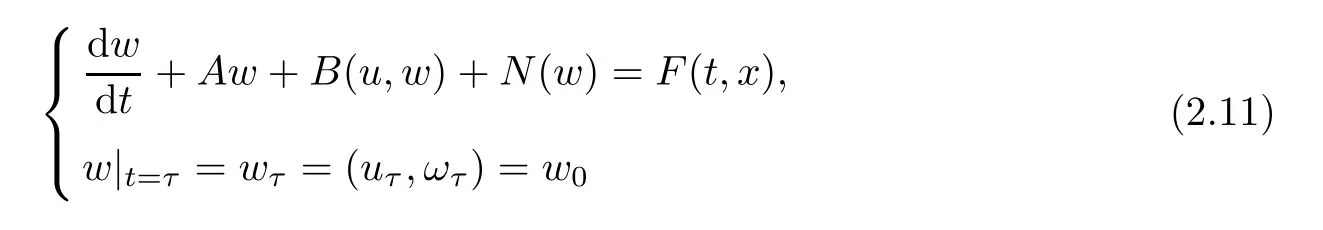
in the sense of distribution in D′(τ,T;).
Lemma 2.4(see[17,28])Assume F(t,x)
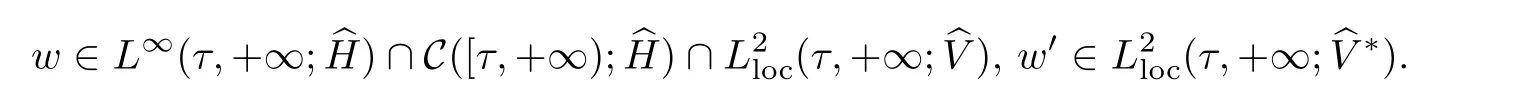
And w depends continuously on the initial value wτwith respect to thebH norm.
(2)If wτ∈problem(1.5)has a unique solution w satisfying
(1)If wτ∈then system(1.5)has a unique solution w satisfying
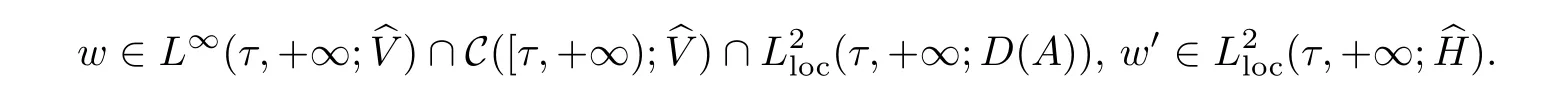
Moreover,the solution w depends continuously on the initial value wτwith respect to thebV norm.
Next,we state the definitions of the process.
Definition 2.5 A biparametric family of maps{U(t,τ)}t>τis called a process on X,which satisfies the following properties
◦U(t,s):X 7→X, for any s 6 t;
◦U(s,s)=identity;
◦U(t,r)U(r,s)=U(t,s) for any s 6 r 6 t.
Moreover,{U(t,s)}t>sis a continuous process on X if,for any t>s,U(t,s)is continuous on X.
Therefore,we have the following facts about the weak solutions of system(1.5):let w be the weak solution of system(1.5),then
(i)w satisfies the “enstrophy equality”
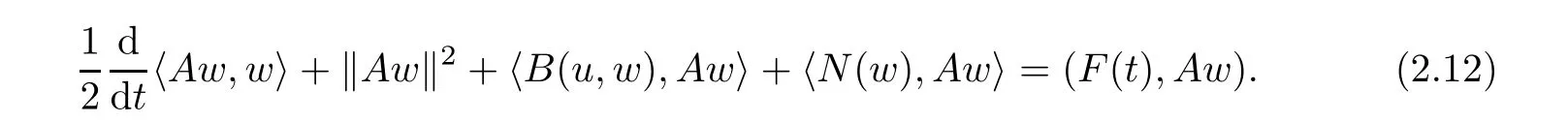
(ii)from Lemma 2.4,the maps defined by

generate a continuous process{UF(t,τ)}t>τinandrespectively.
To end this section,we restate the definitions of the pullback exponential attractor and the global pullback exponential attractor for non-autonomous dynamical systems in the following.Denote by P(X)the family of all nonempty subsets of X.
Definition 2.6(see[21]) A family of sets={M(t):t∈R}⊆P(X)is called a pullback exponential attractor for the process{U(t,τ)}t>τon X if it has the following properties
◦ Compactness:for any t∈R,M(t)is a nonempty compact subset of X.
◦ Positive invariance:U(t,τ)M(τ)⊆ M(t),∀t> τ.
◦Pullback exponentially attracting:pullback exponentially attracts bounded subsets of X,that is,there exists a positive constant c>0,for every t∈R and any bounded subset D⊆X,there exists k>0 such that

◦ Finite fractal dimension:the fractal dimension in X of the sections M(t)is uniformly bounded,that is

where Nǫ(M(t),X)is the minimal number of cubes with length ǫ in X which are necessary to cover M(t).
Definition 2.7(see[21]) A family of sets={A(t):t∈R}⊆P(X)is called a global pullback attractor for the process{U(t,τ)}t>τon X if it has the following properties.
◦Compactness:for any t∈R,A(t)is a nonempty compact subset of X.
◦ Invariance:U(t,τ)A(τ)=A(t),∀t> τ.
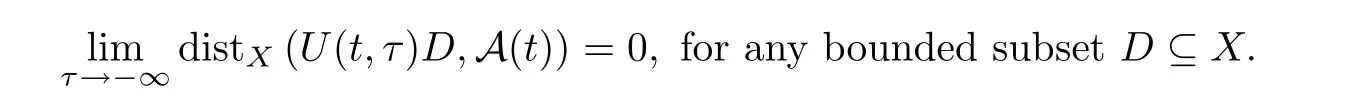
◦ Minimality:the family of setsbA is minimal in the sense that ifbO={O(t):t∈R}⊆P(X)is another family of closed sets such that
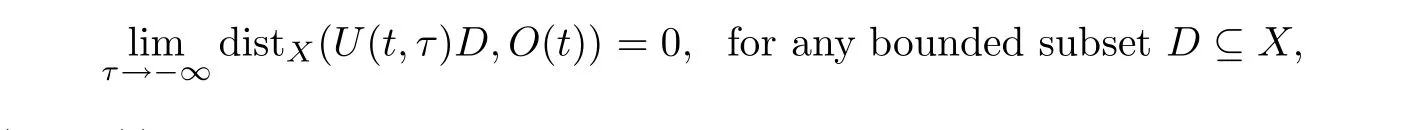
then A(t)⊆O(t)for t∈R.
3 The Key Estimates
In this section,we are going to give the estimates of weak solutions for(1.5).To begin with,let us recall the following Poincaré’s inequality

where λ1>0 represents the first eigenvalue of the operator−∆ in L2(Ω)with domain(Ω)∩H2(Ω)and satisfies the Dirichlet boundary condition,and λ1is a constant depending only onΩ.
Moreover,we also give a weaker assumption of F as follows
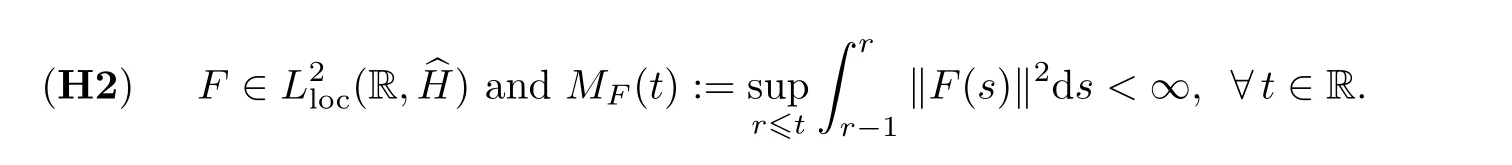
It is obvious that assumption(H1)implies(H2).Then we have the following estimates of the solutions of system(1.5).
Lemma 3.1 Suppose(H2)holds,and let D⊆bH be a bounded subset,then,for any t0∈R,t 6 t0,w0∈D,we have

where
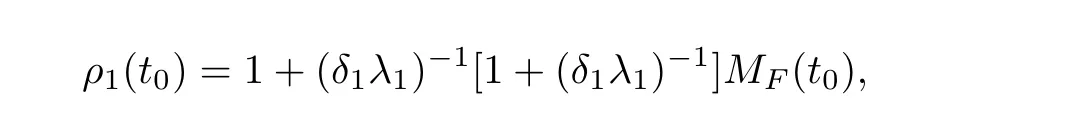
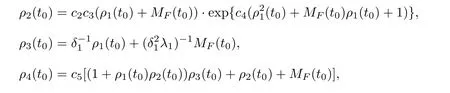
Proof Let w(t)=(u(t),ω(t))be the unique solution of(1.5)corresponding to initial data wτ=(uτ,ωτ) ∈ D.Multiplying(1.5)by w(t)and integrating the resultant equality over Ω,then from(2.7),(2.10),(3.1),Schwartz’s inequality and Young inequality,we have
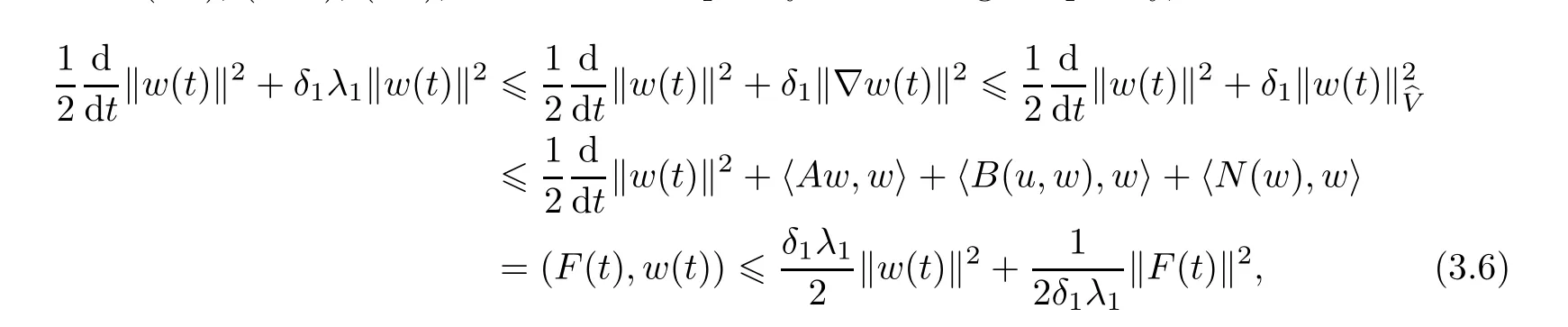
which yields that
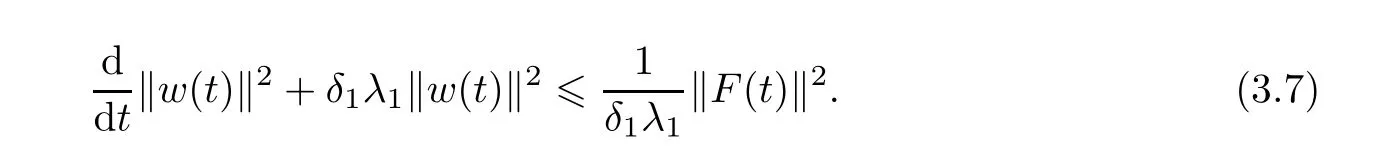
Multiplying(3.7)by eδ1λ1t,then integrating with respect to t,we obtain
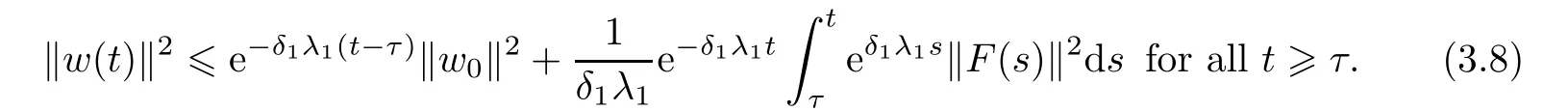
Note that

which together with(3.8)yields
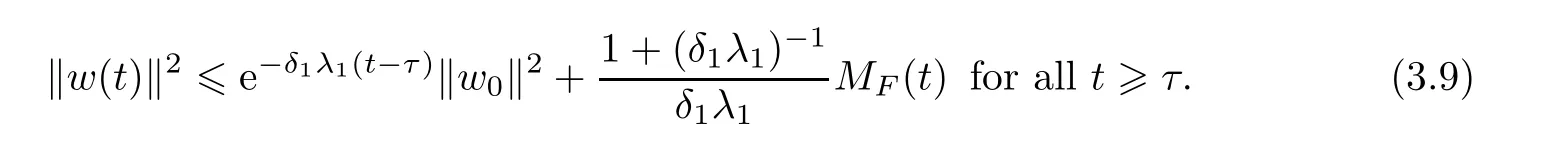
Further,for all t 6 t0,τ 6 t− 2(δ1λ1)−1ln|D|,from(3.9),we have

which immediately implies(3.2).
Next,from(3.6),we also have

Integrating above inequality with respect to t,leads to
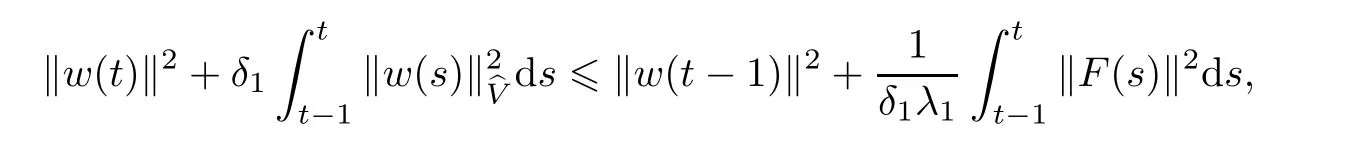
which implies

Therefore,from(3.2),it holds that,for any bounded subset D ⊆ bH,t 6 t0,τ 6 t−1−2(δ1λ1)−1ln|D|,w0∈ D,

This completes the proof of(3.4).
Now let us deal with(3.3).First,for τ Moreover,using Young inequality and taking(2.5)and the fact into account,we can obtain Therefore,equality(3.13)implies Further,using(2.1),we have Then we can rewrite(3.17)as which together with Grownwall’s inequality,we have Integrating(3.18)with respect to s from t−1 to t,one has Therefore,from(2.1)and(3.11),we have which is(3.3). Finally,similar as(3.16),we have which implies Integrating the above inequality with respect to t and using(2.1),we obtain for any t 6 t0,τ In the following,we give the estimates of the difference of solutions and initial data,and that of two solutions. Lemma 3.2 Assume two functions Fi∈and two initial datum w0i∈i=1,2,and we denote by wi(t)=UFi(t,τ)w0i,i=1,2,the corresponding solution of(1.5).Then,for all τ 6 t,it holds For the difference of two solutions of(1.5),we have the following three estimates here ci(i=1,···,9)are positive constants,ν comes from(3.28). with the aid of(2.7).In the following,we estimate the terms on the right-half side of(3.27)one by one.First,we have whereν:=max{ν+νr,α}.From(2.3),(2.10)and(3.14),we obtain Next,it is easy to know from(2.6)and Schwartz’s inequality that Finally,from(3.1),we get Substitution of above four inequalities into(3.27),yields Using Gronwall’s inequality,we deduce that This is(3.22). In order to deal with(3.23),we set w(t)=(u(t),ω(t))=w1(t)− w2(t),then the following equation holds Multiplying(3.29)by w(θ)and integrating the resultant equality over Ω,we have From(2.3),(2.9)and(3.14),we can deduce Moreover,from(3.1),it holds that Combining(2.7)and(3.30)–(3.32),we have Using Gronwall’s inequality to(3.33),we can get for all t> τ that which together with(3.11)implies Next,multiplying(3.29)by Aw(θ),we obtain Due to(2.5),(2.6),(3.1)and(3.14),it holds that and Therefore,using(2.1)and(3.34)–(3.36),we obtain Finally,let us derive(3.25).Without loss of generality,we let τ=0.Then multiplying(3.29)by θAw(θ),we have Similar as(3.35)and(3.36),it is easy to see and From the above three inequalities and(2.1),we obtain where c7is given in(3.37).Using Gronwall’s inequality,we have Moreover,from(3.33),we obtain From(3.10)and(3.23),we also have Hence,the above two inequalities gives where c8comes from(3.38).Further,combining(2.1)and(3.39)–(3.41),we have which implies(3.25).Therefore,we complete the proof of Lemma 3.2. From(3.24)and(3.25)in Lemma 3.2,we immediately have the following results. Corollary 3.3 Assume function F∈(R;),then there exists a positive function G:=G(r1,r2,r3,r4),depending also on Ω and positive constants ν,νr,α,but not on F,such that G ∈ C∞(R4),is increasing in each of the four variables ri,i=1,2,3,4,and for all τ 6 t,w01,w02∈,satisfies In this section,we are going to prove the main result.That is,the existence of pullback exponential attractors with finite fractal dimension for the micropolar fluid flows is shown.To begin with,we consider the family of maps where the process UF(t,τ)defined by(2.13)is restricted toAnd,UF(t,τ):7→is continuous for any τ 6 t,which could be known from estimate(3.24).Then we have Proposition 4.1 Suppose(H2)holds,then there exists a bounded and closed set B⊆and a time sD>0 such that,for all s>sDand any bounded subset D⊆, Proof It is not difficult to get from(3.3)in Lemma 3.1 that Thus,the proof is complete. Further,we obtain Proposition 4.2 Suppose(H2)holds, Proof It follows from(3.3)in Lemma 3.1 and(3.43)in Corollary 3.3. In the following,we also show the following important results with respect to the maps{UF(t,τ)}t>τ. Proposition 4.3 Assume(H1)holds.(I)Continuity with respect to the initial data:There exists a constant CB>0,such that,∀v,w ∈ B,t 6 t0,0 6 s 6 2τ0, (II)Future continuity with respect to the initial data:There exists a constantG(t,D1,D2)>0,such that,for D1,D2bounded subsets ofbV and for any t>t0,v∈D1,w∈D2, (III)Continuity with respect to the forcing terms:There exist C0>0,0< ε06 τ0and γ >0 such that,for all t 6 t0,τ06 r 6 2τ0,0 6 s 6 ε0,v ∈ Oσ(B), (IV)Continuity with respect to the final time:There existsuch that,for all t 6 t0,τ06 r 6 2τ0,0 6 s 6 ε0,v ∈ B, Proof First,from Corollary 3.3,we have,for all t∈R,s> In particular,for all t 6 t0,s∈ [0,2τ0],v,w ∈ B, Therefore,UFsatisfies(I)with Next,UFsatisfies(II)could be got easily from(3.42)in Corollary 3.3. For(III),setting w(t)=UF(t,τ)w0,for any 0 6 s,t− s 6 τ,we have which implies, Moreover,it is easy to get from(2.4),(3.1)and(3.14)that Noting that further,we have From(4.3)and(4.4),therefore,for any t 6 t0,0 6 s 6 1,τ06 r,w0∈ O1(B),we have Obviously, which together with(3.22),(3.23)and the fact∀s∈[0,1],implies that,for any Hence(4.5)–(4.7)yield that there exists a positive constantsuch that,for any t 6 t0,0 6 s 6 1,τ06 r 6 2τ0,w0∈ In the following we verify a bound of the norm of UF(t,τ)w0in,for any t 6 t0,τ 6 t− 1− τ0,w0∈ O1(B).First,from(4.4),we have τ 6 t− 3−ln|O1(B)|.Moreover,from(3.3)and(3.5)in Lemma 3.1,we have which together with(4.2)and Hölder’s inequality,similar as(4.3),yields that there exists a positive constantindependent of t,τ and w0,such that the function Set v(θ)=(θ− t+2)w(θ).It is obvious that v satisfies therefore,from Theorem 2.1 in[15],we deduce that there exists a positive constant C=C(ν,νr,α,Ω,q),independent of t,τ and w0,such that moreover,we also note that Therefore,we deduce from(4.11)and(4.12)that which together with(4.9)and(4.10)implies that there exists a positive constantbC4,independent of t,τ and w0,such that Due to the equivalence of kAwk and kwk(H2(Ω))3,(4.13)implies w′(θ) ∈ Lq(t− 1,t;bH)and w(θ)∈ Lq(t−1,t;D(A)).Then,from Theorem 1.4 in[1]and the compact embedding relationship: Therefore,for any t 6 t0−1,τ 6 t−τ0,w0∈ O1(B), Applying the interpolation inequality,we have Finally,let us deal with(IV).Similarly,it follows from(4.5)and(4.14)–(4.15)that,for any t 6 t0−1,0 6 s 6 1,τ06 r 6 2τ0,w0∈ O1(B), On the basis of the above three propositions and using Theorem 2.3 in[21],we immediately have the following results. Lemma 4.4 Assume(H1)holds,UF,t0defined by(4.1)is a process onbV,then the family cM={MUF(t):t∈R}defined by satisfies (1)UF(t,τ)MUF(τ) ⊆ MUF(t)for all τ 6 t. (2)MT−τUF(t)=MUF(t− τ)for all τ>0 and any t 6 t0− 1,where T−τUF(t,s):=UF(t−τ,s−τ). Proof Under assumption(H1),Propositions 4.1–4.3 are valid.From Propositions 4.2 and 4.3(I),one can verify(1)and(2).Propositions 4.2 and 4.3(I)(II)imply(3).Proposition 4.1 together with Proposition 4.3 yields(4).For the detailed proof one can see the proof of Theorem 2.3 in[21],we omit here.This completes the proof. ? Now let us give the proofs of our main results as follows. Proof of Theorem 1.1 According to the Definition 2.6,Theorem 1.1 follows directly from Lemma 4.4. ? Proof of Theorem 1.2 The existence of the global pullback attractorsbA for UFis based on the definition 2.7 and Lemma 4.4.Further,by comparing Definition 2.6 and Definition 2.7,one has In particular,as a consequence of Theorem 1.1,it holds that Therefore,the proof of Theorem 1.2 is completed.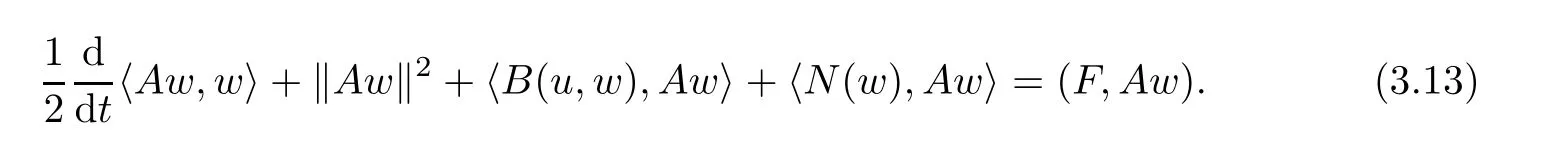
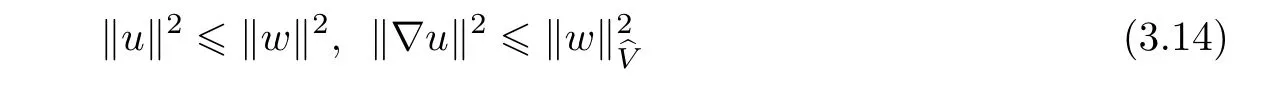






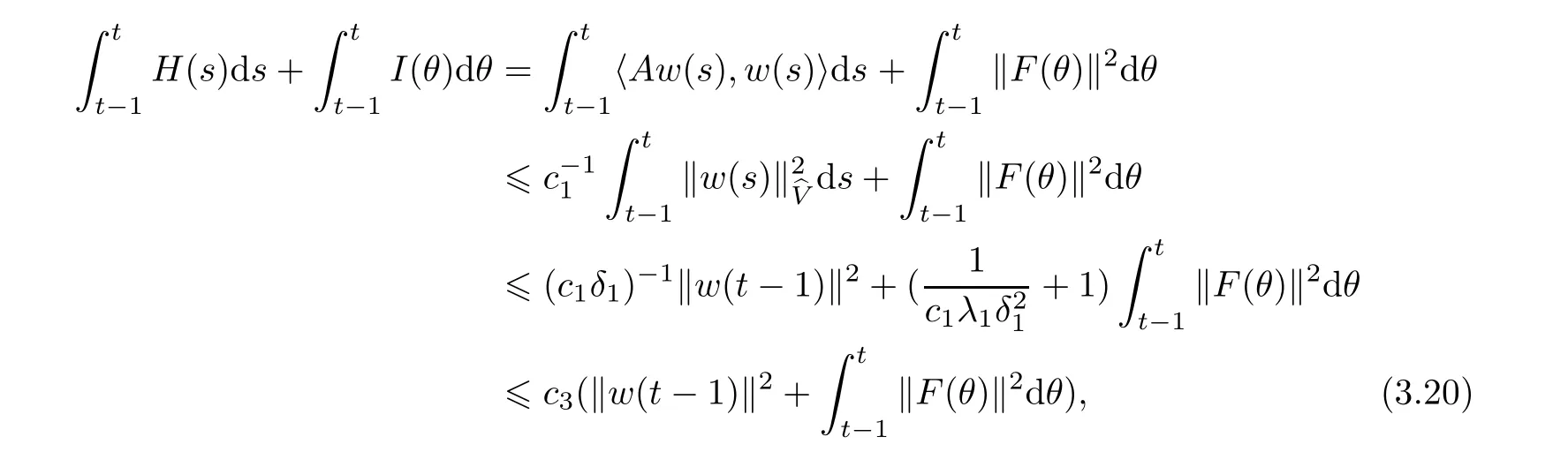
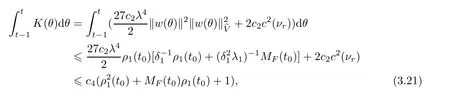
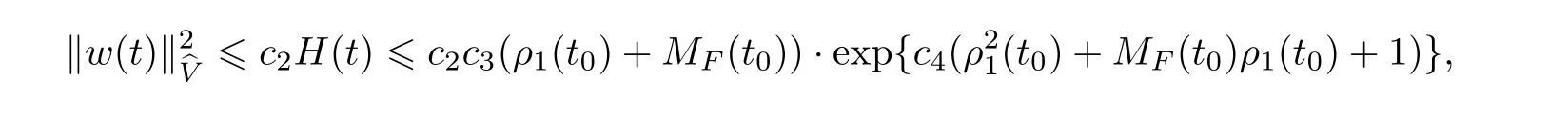
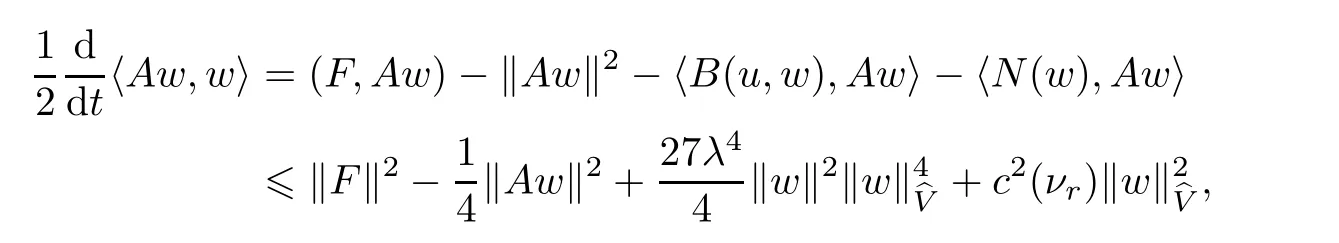
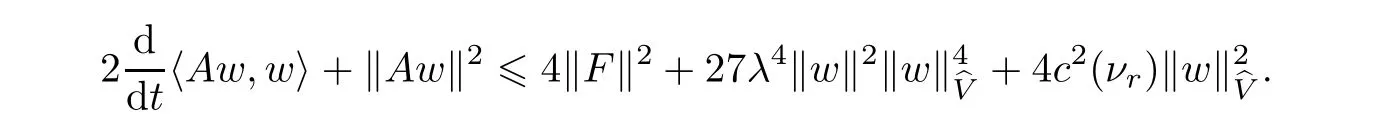
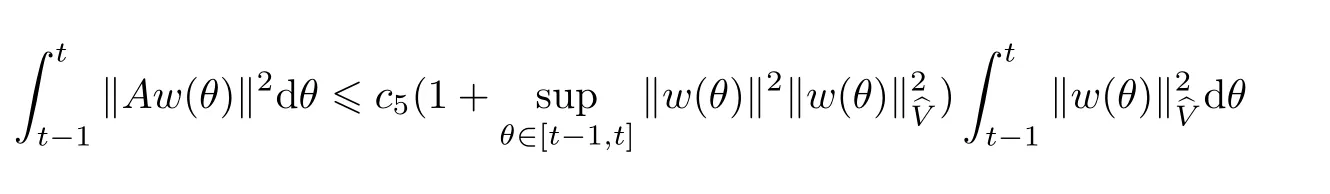


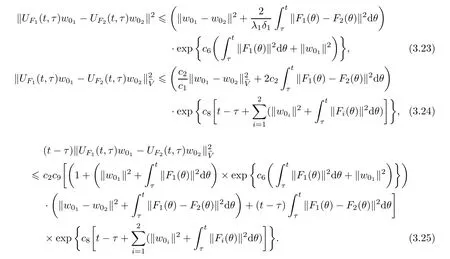

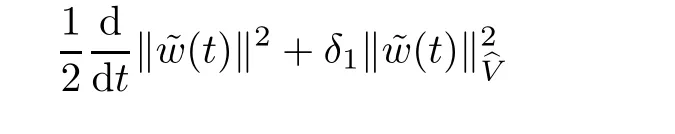

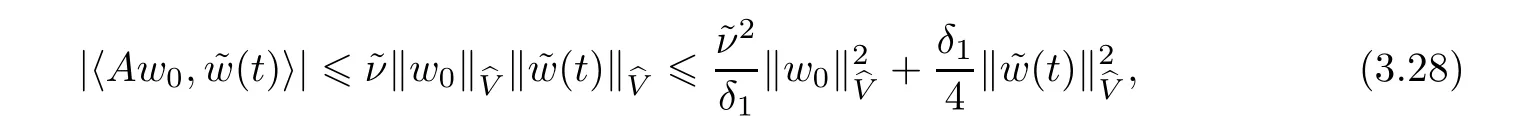
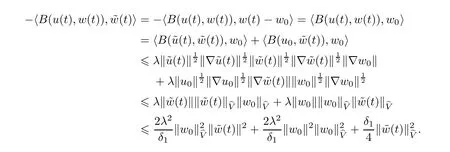
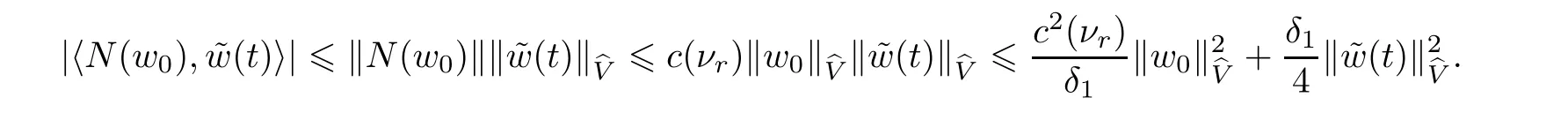

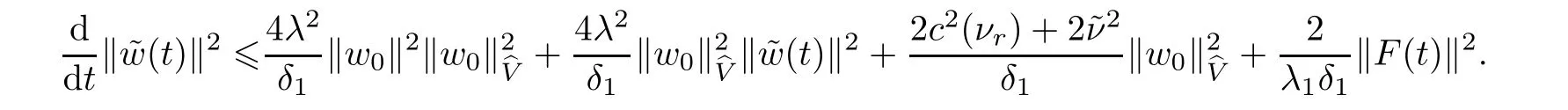

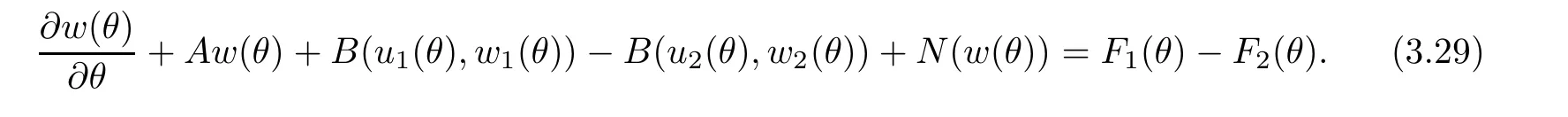
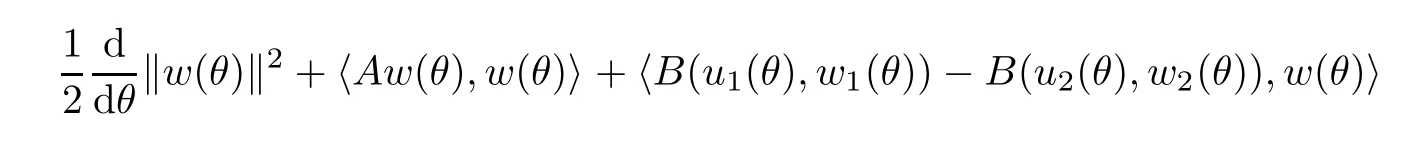
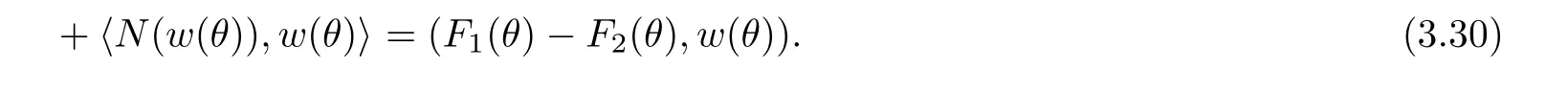
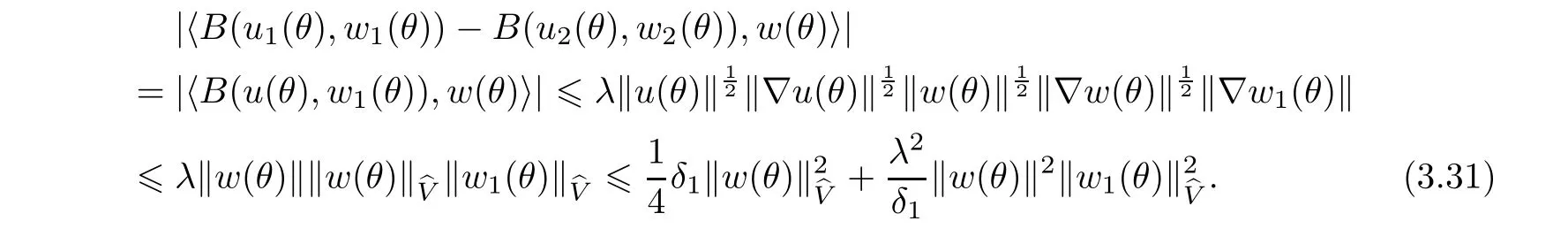
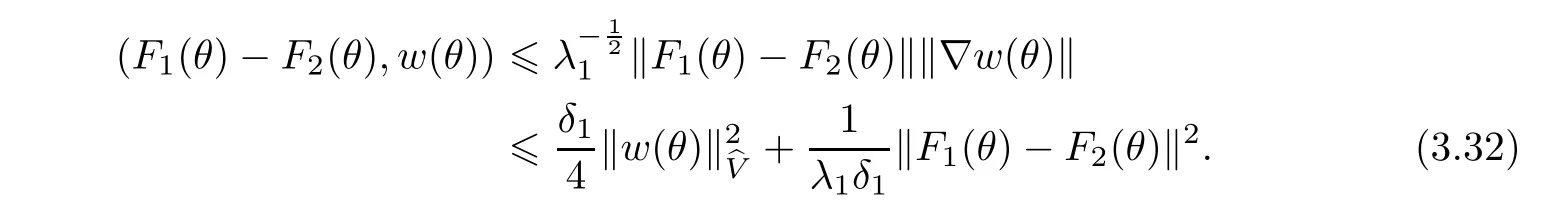
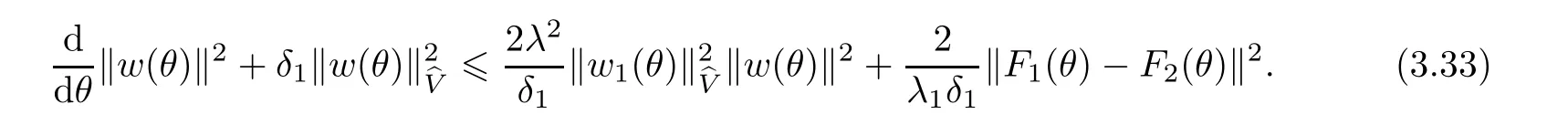

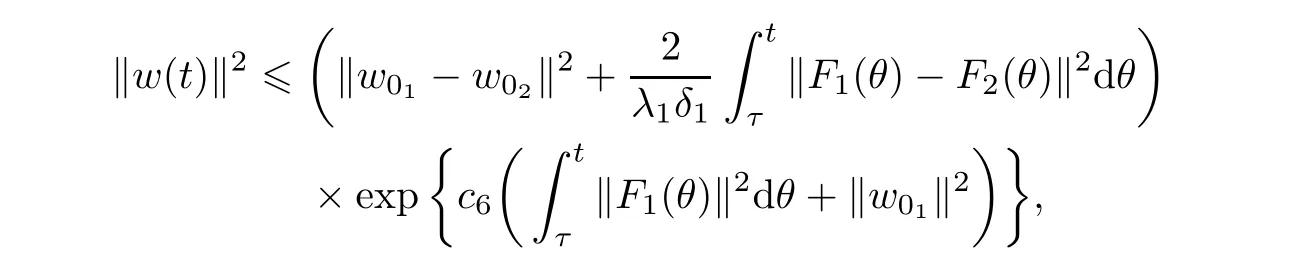
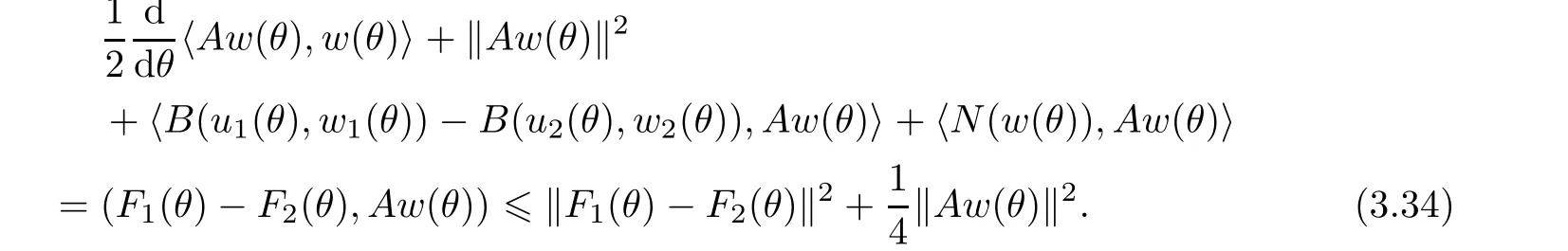

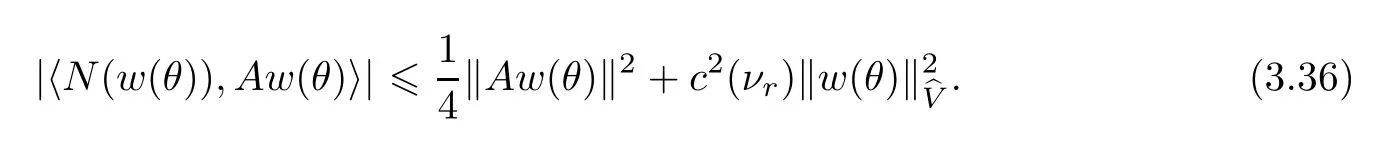


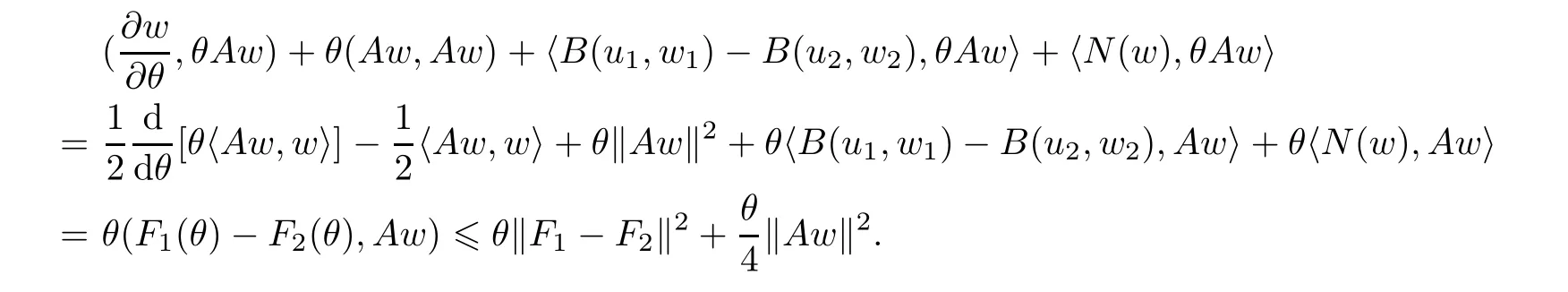
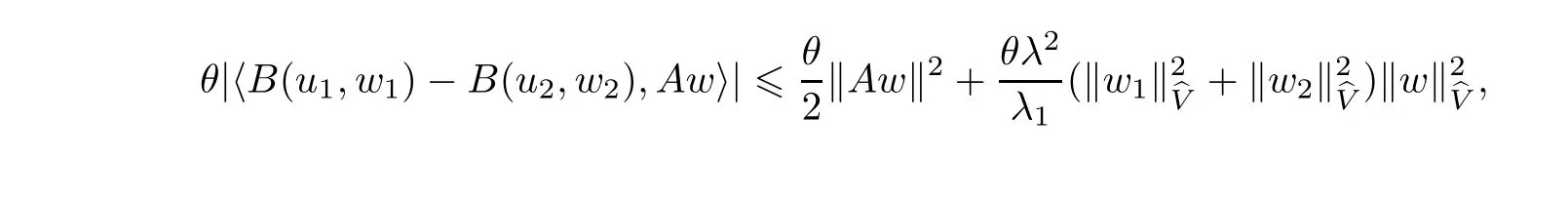
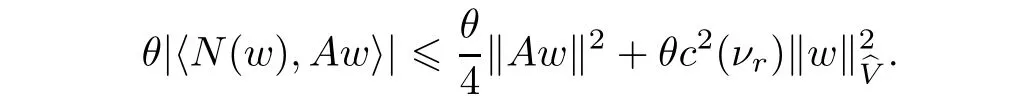




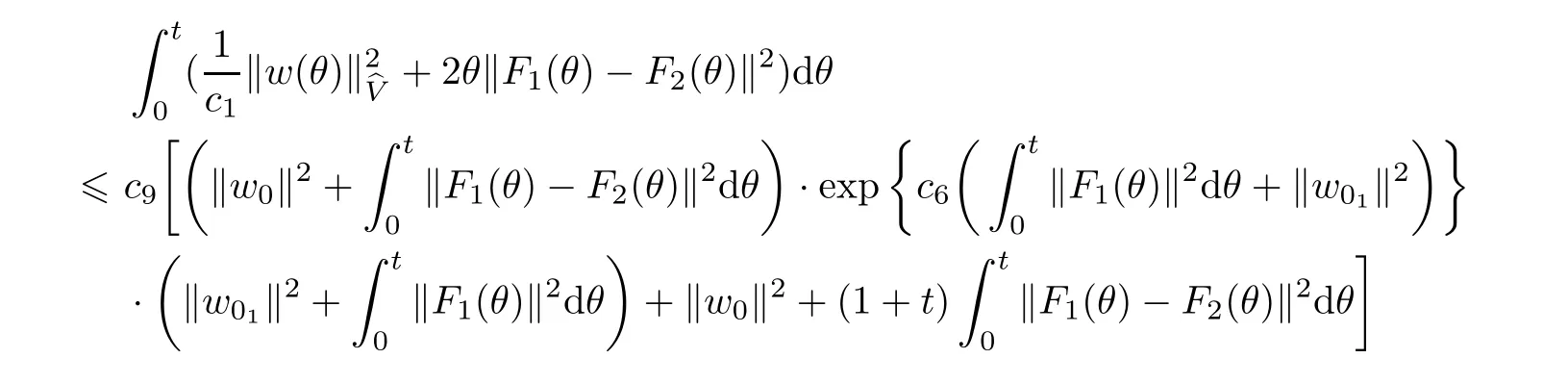


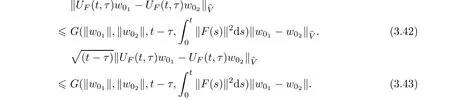
4 The Proof of Theorems 1.1 and 1.2

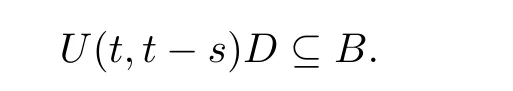


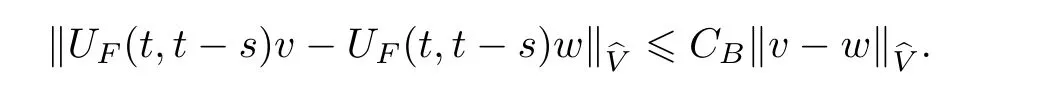
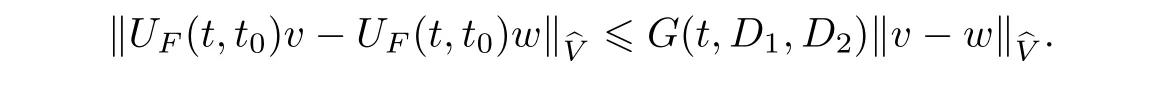

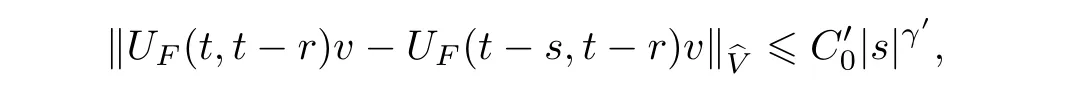
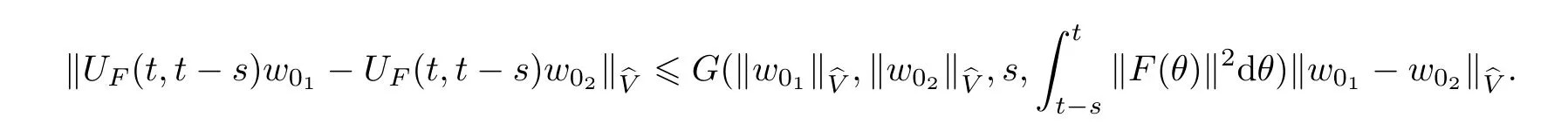



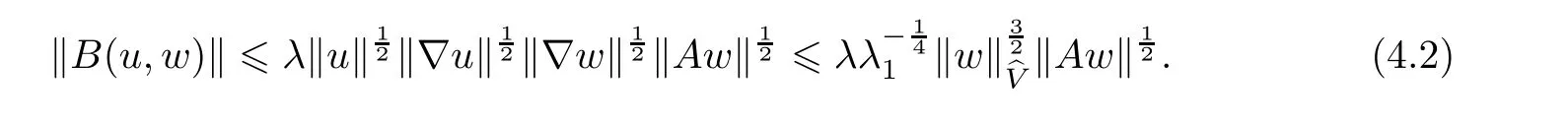

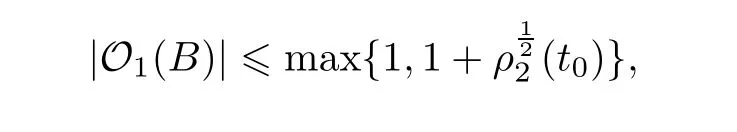



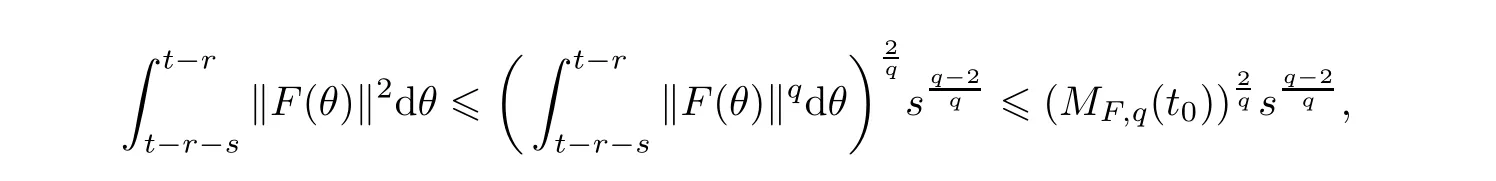
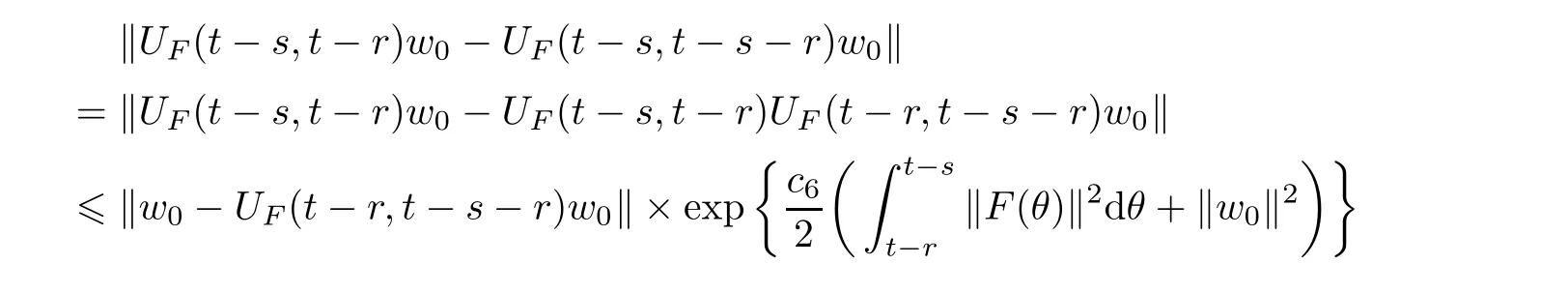
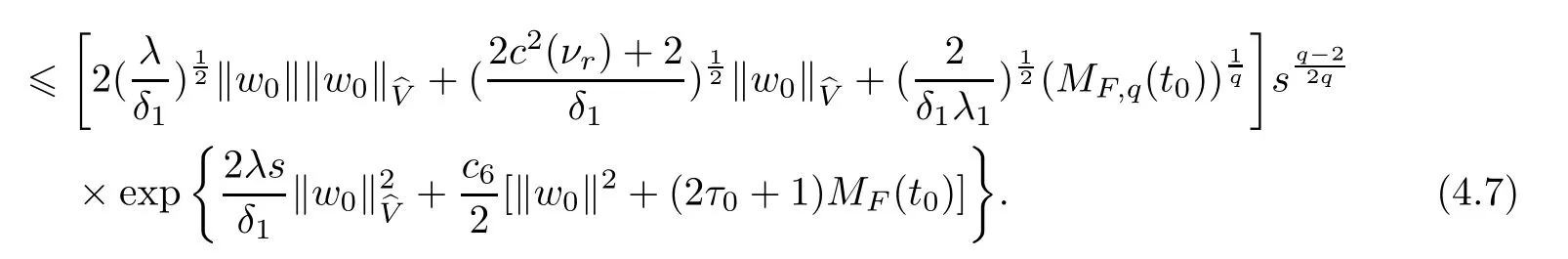
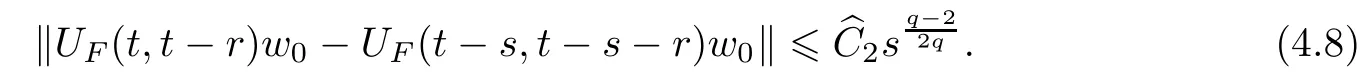

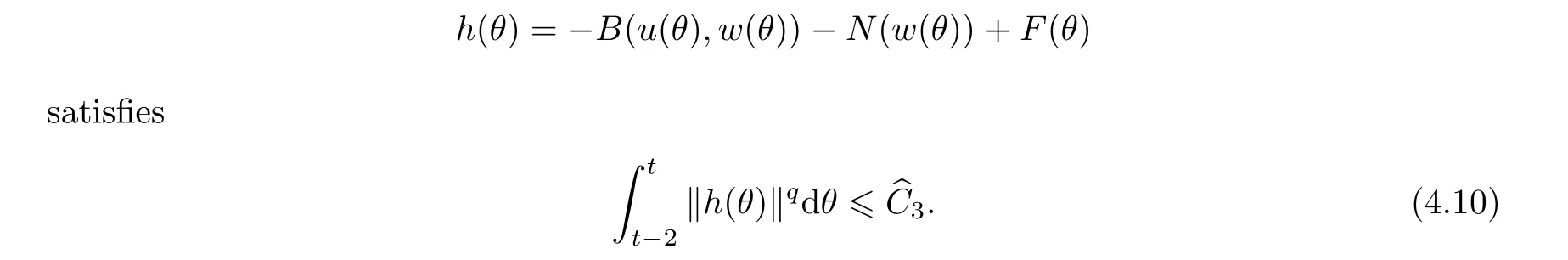
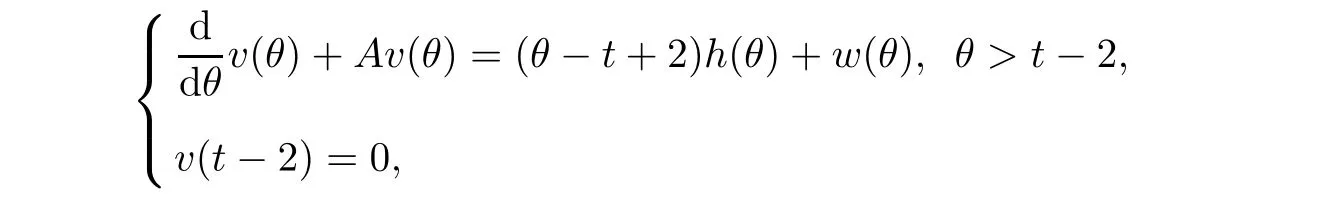



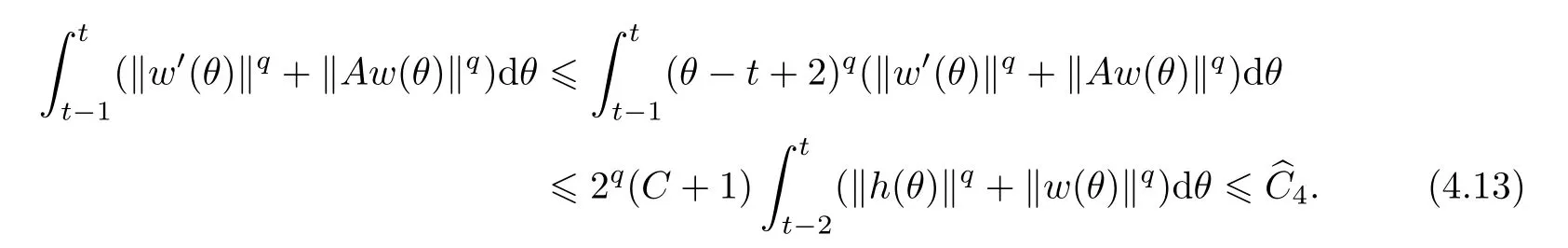
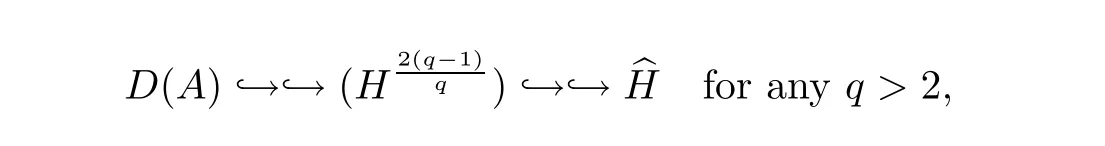



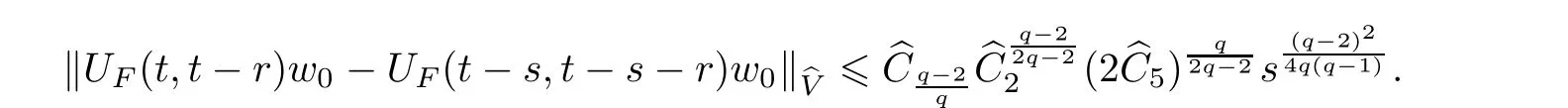

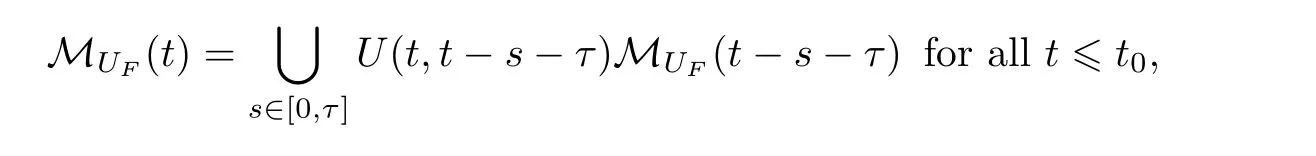
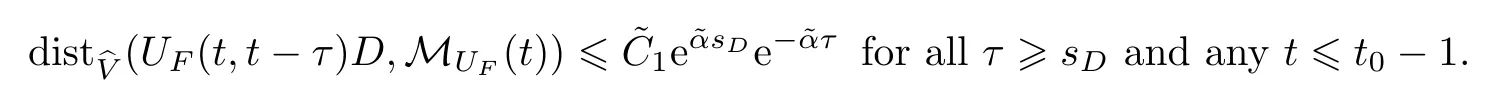


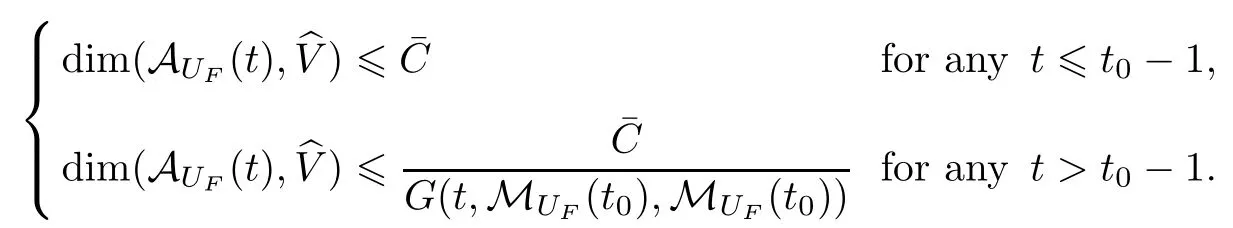
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- WEIGHTED COMPOSITION OPERATORS ON THE HILBERT SPACE OF DIRICHLET SERIES∗
- GENERALIZED DISCRETE Q-HERMITE I POLYNOMIALS AND Q-DEFORMED OSCILLATOR∗
- ON THE FINITE MELLIN TRANSFORM IN QUANTUM CALCULUS AND APPLICATION∗
- OPTIMAL ERROR ESTIMATES OF A DECOUPLED SCHEME BASED ON TWO-GRID FINITE ELEMENT FOR MIXED NAVIER-STOKES/DARCY MODEL∗
- PARAMETER IDENTIFICATION BY OPTIMIZATION METHOD FOR A POLLUTION PROBLEM IN POROUS MEDIA∗
- DEVIATION OF THE ERROR ESTIMATION FOR VOLTERRA INTEGRO-DIFFERENTIAL EQUATIONS∗
