CHAIN CONDITIONS FOR C∗-ALGEBRAS COMING FROM HILBERT C∗-MODULES∗

Mahmood POURGHOLAMHOSSEIN Mohammad ROUZBEHANI

Department of Mathematics,Faculty of Sciences,University of Qom,Qom,Iran

E-mail:m-purghol@qom.ac.ir;mrouzbehani@stu.qom.ac.ir

Massoud AMINI

Department of Mathematics,Faculty of Mathematical Sciences,Tarbiat Modares University,14115-134 Tehran,Iran

E-mail:mamini@modares.ac.ir

Abstract In this paper we define and study chain conditions for Hilbert C∗-modules through their C∗-algebras of compact operators and discuss their perseverance under Morita equivalence and tensor products.We show that these chain conditions are passed from the C∗-algebra to its Hilbert module under certain conditions.We also study chain conditions for Hilbert modules coming from inclusion of C∗-algebra with a faithful conditional expectation.

Key words Hilbert C∗-module,Noetherian and Artinian C∗-algebras,purely infinite C∗-algebras,Morita equivalence

1 Introduction

Chain conditions for a C∗-algebra[7]are defined in its set of closed(two-sides)ideals,while in an earlier definition,they are defined for its closed left ideals[26].The main goal of this paper is to extend chain conditions to Hilbert C∗-modules.

Hilbert C∗-modules were first appeared in the work of Kaplansky[10]in the commutative case,and later in[20]and[22]for general C∗-algebras(independently)and soon found applications in dilation theory[11]and Morita equivalence[24].It now plays a significant role in K-theory and KK-theory,as well as representation theory(via Morita equivalence)[14,16].

Let A be a C∗-algebra.A Hilbert C∗-module E over A(or a Hilbert A-module)is a vector space over C and a right A-module with compatible scalar multiplication equipped with an A-valued inner product satisfying

Let A be a C∗-algebra and E be a Hilbert A-module.Let LA(E)be the C∗-algebra of adjointable operators on E.Every element of LA(E)is a bounded A-linear map.Let KA(E)be he closed linear span of the set of all elementary operators θx,y:E → E given by θx,y(z)=x;x,y,z ∈ E.The elements of KA(E)are called compact(adjointable)operators.KA(E)is a closed ideal in LA(E)and so is a C∗-algebra.The linking algebra of E is denoted by L(E)(c.f.,[21],p.51).

A Hilbert C∗-module E is called(algebraically) finitely generated if there exists a finite set S⊆E such that E equals the linear span(over C and A)of this set([16],p.8).If S is a countable set and E is the closed span of S.A,then E is called countably generated.

Let E′be the set of all bounded A-inear maps from E to A.This set is itself a right A-module by the scalar multiplication(λf)(x)=λf(x)and the module action(f.a)(x)=a∗f(x),for λ ∈ C,f ∈ E′,x ∈ E([20],p.450).This is called the dual(Banach)module of E.A Hilbert A-module E is called self-dual if E=E′.

Let A and B be two C∗-algebras.An A-B-imprimitivity bimodule X is an A-B-bimodule such that

(i)X is a full left Hilbert A-module and a full(right)Hilbert B-module,

for x,y,z∈X,a∈A,b∈B.

Two C∗-algebras A and B are called(strongly)Morita equivalent if there exists an A-B-imprimitivity bimodule.Rieffel called a pair of algebras admitting an imprimitivity bimodule strongly Morita equivalent,and used Morita equivalence to mean that the two C∗-algebras had isomorphic categories of representations on Hilbert space.Here,Morita equivalence always means strong Morita equivalence in the sense of Rieffel.Morita equivalence preserves several properties of C∗-algebras such as nuclearity and simplicity but it is weaker than the notion of C∗-isomorphism[3,8].For more details on Hilbert C∗-modules see[14,16,21].

2 Chain Conditions on Ideals

Chain conditions for a C∗-algebra are defined in its set of closed(two-sides)ideals.A C∗-algebra A is called Noetherian if it satisfies the ascending chain condition for closed ideals,that is,for any ascending chain I1⊆ I2⊆ I3⊆ ···of closed ideals of A,there is an integer n such that Ii=Infor all i≥ n.The dual notion to a Noetherian C∗-algebra is an Artinian C∗-algebra,which satisfies the descending chain condition for closed ideals.

Definition of a Noetherian C∗-algebra differs from the traditional definition of a Noetherian Banach algebra,which imposes the same chain condition on the set of closed left ideals.In[26],it was shown that every Noetherian Banach algebra is finite dimensional.This result is still true for commutative C∗-algebras,but not in general.In[7],there are examples of infinitedimensional Noetherian C∗-algebras.Clearly,every C∗-algebra with finitely many ideals is Noetherian and Artinian,such as simple C∗-algebras.Examples of nontrivial Noetherian C∗-algebras(i.e.,the Noetherian C∗-algebras with infinitely many closed ideals)are given in[7].

Each C∗-algebra A is a Hilbert C∗-module over itself with respect to the inner product ha,biA=a∗b(a,b∈ A).This provides the motivation for extending chain conditions to Hilbert C∗-modules.Of course,we cannot define Noetherian Hilbert C∗-modules directly based on ascending chain conditions on closed submodules,since closed submodules of a C∗-algebra A(as a Hilbert A-module)correspond to closed right ideals in A.Instead,we use the following definition.

Definition 2.1 Let A be a C∗-algebra.A Hilbert A-module E is called Noetherian(resp.Artinian)if C∗-algebra KA(E)is Noetherian(resp.Artinian).

A C∗-algebra A is Noetherian(resp.Artinian)as a Hilbert A-module if and only if it is Noetherian(resp.Artinian)as a C∗-algebra,because we have KA(A) ∼=A(see[16],Proposition 2.2.2).

If I is a closed ideal in C∗-algebra A,then a ideal submodule for E,denoted by EI,is defined as follows

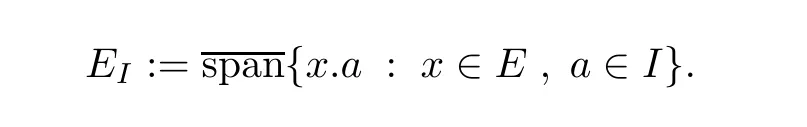
This is a closed submodule of E.Indeed EI=E.I=E.I={x.a:x∈E,a∈I}(see[2],Definition 1.1 and Proposition 1.2).

It’s worth mentioning that for a C∗-algebra A,considered as a Hilbert A-module,the ideal submodules are precisely the closed ideals.

If A is a C∗-algebra and S ⊆ A,then the closed ideal I generated by S is the smallest closed ideal containing S(see[17],p.4).

Lemma 2.2 A C∗-algebra A is Noetherian(resp.Artinian)if and only if every hereditary C∗-subalgebra of A is Noetherian(resp.Artinian).

Proof Let D be a hereditary C∗-subalgebra of A and J be a closed ideal in D.We set

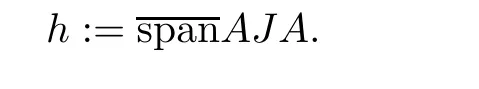
Then h is a closed ideal in A contained in k=ADA.Let Id(D)be the set of closed ideals in D and Idk(A)be the set of closed ideals in A contained in k.We know that the map

is a bijection(see[4],p.90).Therefore,the ascending(resp.descending)chain J1⊆J2⊆J3⊆ ···(resp.J1⊇ J2⊇ J3⊇ ···)of closed ideals of D stabilizes,because A is Noetherian(resp.Artinian).Thus D is Noetherian(resp.Artinian).The converse is clear. ?

This lemma implies that a C∗-algebra A is Noetherian(resp.Artinian)iffevery closed ideal in A is Noetherian(resp.Artinian),because a closed ideal is also a hereditary C∗-subalgebra.

Proposition 2.3 Let A be a C∗-algebra.A Hilbert A-module is Noetherian(resp.Artinian)if and only if any of its ideal submodules are Noetherian(resp.Artinian).

Proof Let E be a Noetherian(resp.Artinian)Hilbert A-module,I a closed ideal in A and EIan ideal submodule of E.According to the previous definition,C∗-algebra KA(E)is Noetherian(resp.Artinian).On the other hand,KA(EI)is(up to isomorphism)a hereditary C∗-subalgebra of KA(E)(see[15],Lemma 2.13).Now KA(EI)is Noetherian(resp.Artinian),by the previous lemma,and so EIis Noetherian(resp.Artinian).The converse is clear. ?

Let A and B be two C∗-algebras,I be a closed ideal in B and X an A-B-imprimitivity bimodule.In this case,X.I is a closed A-B-submodule of X andAhX.I,X.Ii(taking the closed span)is a closed ideal of A.In addition,if X∗is dual(or adjoint)module of X(see[21],p.49)and we set then L(X.I)is a closed ideal of linking algebra L(X).

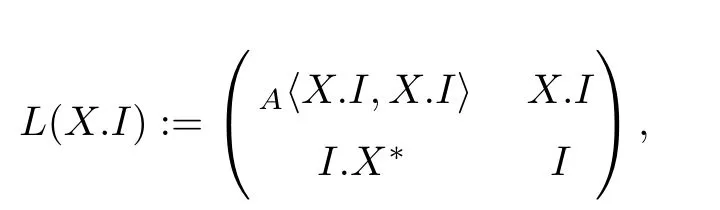
Theorem 2.4 Let A and B be two C∗-algebras and X an A-B-imprimitivity bimodule.Then the following assertions are equivalent

(i)A is Noetherian(resp.Artinian);

(ii)B is Noetherian(resp.Artinian);

(iii)L(X)is Noetherian(resp.Artinian);

(iv)KA(X)is Noetherian(resp.Artinian);

(v)KB(X)is Noetherian(resp.Artinian).

Proof In the above notations,the maps I 7−→Aand I 7−→ L(X.I)provide inclusion preserving bijective correspondences between the closed ideals of B,the closed ideals of A and the closed ideals of the linking algebra L(X),respectively(see[21],§3.3).Thus(i)⇔ (ii)⇔ (iii).On the other hand,since X is an A-B-imprimitivity bimodule and X∗is a B-A-imprimitivity bimodule,then KB(X) ∼=A and KA(X∗) ∼=B(see[21],Proposition 3.8).But KA(X)KA(X∗)(via x∗T=(T∗x)∗),therefore(i) ⇔ (v)and(ii) ⇔ (iv). ?

As stated in the introduction,two C∗-algebras A and B are called Morita equivalent if there exists an A-B-imprimitivity bimodule(see[16],Definition 1.5.5).Two Hilbert C∗-modules E and F,respectively,over C∗-algebras A and B are Morita equivalent,E ∼MF,if the C∗-algebras KA(E)and KB(F)are Morita equivalent(see[9],Definition 2.1).Morita equivalence in the classes of C∗-algebras or Hilbert C∗-modules is an equivalence relation(see[14],Proposition 7.5 and[9],p.3).

Corollary 2.5 Noetherian(resp.Artinian)property is preserved under Morita equivalence of C∗-algebras and Hilbert C∗-modules.

Proof Let A be a Noetherian(resp.Artinian)C∗-algebra,B be a C∗-algebra,E be a Noetherian Hilbert A-module and F be a Hilbert B-module.If A∼MB,there is an A-B-imprimitivity bimodule.Thus,it follows from the previous theorem that B is Noetherian(resp.Artinian).If E ∼MF,then KA(E)∼MKB(F).Since KA(E)is Noetherian(resp.Artinian),KB(F)is also Noetherian(resp.Artinian)and so F is Noetherian(resp.Artinian). ?

Let{Hn}be a set of Hilbert spaces and{An}be a set of C∗-algebras.Then Hilbert space H and C∗-algebra A are defined as follows Of course,A is a closed ideal in

(see[4]).

Example 2.6The C∗-algebrais not Noetherian as a Hilbert A-module,because C CC2CC2C3···is a strictly ascending chain of closed ideals of KA(A)∼=A.Also,ideal submoduleis not Noetherian.Therefore,C∗-algebras C and A are not Morita equivalent as Hilbert C∗-modules in the sense of(see[9],Definition 2.1),by Corollary 2.5.But Hilbert spaces C andare Morita equivalent as Hilbert C-modules,since KC(C)∼MKC(H).Furthermore,for A and H as Hilbert C-modules and B=K(H)as a Hilbert B-module,we have A≁MH ∼MB.

Theorem 2.7 Let A be a C∗-algebra and E be a Hilbert A-module.Then the following assertions are equivalent

(ii)E is Noetherian(resp.Artinian);

(iii)L(E)is Noetherian(resp.Artinian);

(iv)Each ascending(resp.descending)chain of ideal submodules of E stabilizes;

(v)Each non-empty set of ideal submodules of E has a maximal(resp.minimal)element.

Proof Since each Hilbert A-module E is itself a KA(E)-hE,EiA-imprimitivity bimodule(with KA(E)-valued inner productKA(E)hx,yi:= θx,y;θx,y∈ KA(E)),Theorem 2.4 implies(i)⇔(ii)and(i)⇔(iii).There is a natural bijective correspondence between the set of all ideal submodules of a Hilbert C∗-module E and the set of all closed ideals of the corresponding linking algebra L(E)[2].Thus(iii)⇔ (iv).For(iv)⇒ (v),let(iv)holds and Γ be a non-empty set of ideal submodules of E.Since Γ 6= ∅,there exists EI1∈ Γ.If EI1is maximal(resp.minimal),the implication holds.Otherwise,there exists EI2∈Γ such that EI1⊆EI2(resp.EI1⊇EI2).By continuing this process,we will obtain an ascending(resp.descending)chain EI1⊆ EI2⊆ EI3⊆ ···(resp.EI1⊇ EI2⊇ EI3⊇ ···)of ideal submodules of E.Now,by assumption,this chain stabilizes and so there is a n∈N such that EIn∈Γ is maximal(resp.minimal).(v)⇒(iv)is clear. ?

According to this theorem,a full Hilbert A-module E is Noetherian(resp.Artinian)if and only if A is so.

Let the set HA={(ai)i∈N:ai∈ Aconverges in A}be the canonical countably generated Hilbert A-module(see[16])and K denote the C∗-algebra of compact operators on a separable Hilbert space H.

Lemma 2.8 Let A be a separable C∗-algebra and E a Hilbert A-module.Then KA(E)is σ-unital iff it is separable.

Proof Let KA(E)be σ-unital.Then E is countably generated(see[14],Proposition 6.7).Thus E ⊕ HA∼=HA,by Kasparov’s stabilization theorem(see[14],Theorem 6.2).On the other hand,KA(HA)is separable,because KA(HA)∼=K ⊗ A(see[14],p.63).Therefore,KA(E)is also separable.Since every separable C∗-algebra is σ-unital(see[4],p.81),the converse holds.

A topological space is Noetherian if it satisfies the ascending chain condition for open subsets(equivalently,if every family of open subsets contains a maximal element).Let Prim(A)be the set of primitive ideals in C∗-algebra A.Then Prim(A),with the hull-kernel topology(or Jacobson topology),is a topological space(see[17],p.159).If A and B are C∗-algebras,then we write A⊙B for their algebraic tensor product.We denote the completion of A⊙B with respect to the spatial(minimal)C∗-norm by A⊗B.We say a C∗-algebra A is nuclear if,for each C∗-algebra B,there is only one C∗-norm on A⊙B[4].

Theorem 2.9 Let A and B be two C∗-algebras.Then

(i)if A is Noetherian,then the topology on Prim(A)has a basis consisting of compact-open sets;

(ii)if A and B are separable and either A or B is nuclear,then A and B are Noetherian iff A⊗B is Noetherian.In particular,A is Noetherian iff Mn(A)is so,and also A is Noetherian iff A⊗K is so;

(iii)in general,if A and B are Noetherian,then A⊗B is not necessarily Noetherian.

Proof (i) We know that a C∗-algebra A is Noetherian if and only if Prim(A)is a Noetherian topological space(see[7],Lemma 2.2).Now,since Prim(A)is Noetherian,each open set in Prim(A)is compact[6],and so each element of the basis is both compact and open.

(ii)Let A and B be Noetherian.Since product of two Noetherian spaces is Noetherian[6],Prim(A)× Prim(B)is Noetherian.But we have a homeomorphism Prim(A)× Prim(B)∼=Prim(A⊗B)([21],Theorem B.45).Thus Prim(A⊗B)is also Noetherian.Conversely,let A⊗B be Noetherian but A(or B)is not Noetherian.In this case,since Prim(A)is not Noetherian,it has an open set U which is not compact.If V is an open set in Prim(B),then(U×V)is an open set in Prim(A)× Prim(B) ∼=Prim(A ⊗ B)which is not compact.Thus we obtain a contradiction.The last assertion holds,because Mn(A) ∼=Mn(C) ⊗ A and two C∗-algebras Mn(C)and K are simple,separable and nuclear.

(iii)Let D be the Dadarlat’s non-exact,separable,simple,unital C∗-algebra(see[18],§2.1)and A be the non-exact,separable,unital C∗-subalgebra of B(H),constructed in Theorem 2.6 of[18].Then Prim(A)consists of two points and Prim(A⊗D)does not have a basis for its topology consisting of compact-open sets(see[19],Proposition 4.5(i)).Thus C∗-algebras A and D are Noetherian,but A⊗D is not Noetherian,by(i). ?

Remark 2.10 It is not true that every Noetherian C∗-algebra is separable.For example,the Calkin algebra(i.e.,the quotient B(H)/K(H),on a separable infinite-dimensional Hilbert space H)is simple(and so Noetherian),but it is not separable.

Suppose that A and B are C∗-algebras,E is a Hilbert A-module,F is a Hilbert B-module.Let us briefly recall the construction the interior and exterior tensor products of E and F.

Let ϕ :A −→ LB(F)be an ∗-homomorphism.Then F could be considered as a left A-module,via a·y=ϕ(a)(y),for y∈F and a∈A.Consider the algebraic tensor product E⊙AF as a right B-module with action(x⊗y)·b=x⊗(y·b).Define

for x,x′∈ E,y,y′∈ F,extended B-linearity on E ⊙AF.The completion is a Hilbert B-module E ⊗ϕF,called the interior tensor product of E and F(via ϕ).There is a canonical∗-homomorphism π :LA(E)→ LB(E⊗ϕF),given on the algebraic tensor products by π(T)(x⊗y)=T(x)⊗ y.This is injective when ϕ is so.

The exterior tensor product E⊗F of E and F is defined directly.The algebraic tensor product E ⊙F is a right A⊙B-module via(x⊗y)·(a⊗b):=(x·a)⊗(y·b)and

for x,x′∈ E,y,y′∈ F,extended by linearity.There is a canonical∗-homomorphism σ :LA(E)⊗ LB(F)→ LA⊗B(E ⊗ F),given on the algebraic tensor products by σ(S ⊗ T)(x⊗y)=S(x)⊗T(y).Here we have used the minimal tensor norm for the completion,but the construction could be carried out for any C∗-norm on A⊙B[14].

A C∗-algebra A is infinite if A has an infinite projection and purely infinite if the hereditary C∗-subalgebra xAx contains an infinite projection,for each nonzero positive element x of A.Clearly,if A is purely infinite,then it is infinite and every hereditary C∗-subalgebra of A is purely infinite.The notion of purely infinite C∗-algebras could also be defined in terms of the Cuntz comparison.Let A+be the positive cone of A.For a,b∈A+we write a-b if there is a sequence(xk)⊆ A such that x∗kaxk→ b,as k → ∞.Now a C∗-algebra A is purely infinite iffthere is no character on A and for all a,b∈A+such that a belongs to the closed linear span of AbA,we have a-b[4].

Example 2.11 Assume that E is a Hilbert C∗-module over a Kirchberg algebra A that is a simple,separable,nuclear,purely infinite C∗-algebra(for instance,see theorem 6.11 of[25]).The Cuntz algebra O∞is a unital,simple,nuclear,purely infinite C∗-algebra and so A⊗O∞ ∼=A(see[4],Theorem V.2.2.3).Since A is simple,E is full and so,A=hE,EiA∼MKA(E).Furthermore,properties of simplicity,nuclearity and being purely infinite are preserved under Morita equivalence.Thus

In particular,the Hilbert C∗-modules E and E⊗O∞are Noetherian and Artinian and in fact,E∼ME⊗O∞.

Theorem 2.12 Assume that A and B are separable C∗-algebras that either A or B is nuclear.Also,assume that E and F are countably generated Hilbert C∗-modules,respectively,over C∗-algebras A and B.Then

(i)if A and B are Noetherian,then E⊗F is also Noetherian.In particular,the standard Hilbert B-module HBis Noetherian;

(ii)if E and F are full and Noetherian,then A⊗B and E⊗F are also Noetherian.

Proof (i)Since A and B are Noetherian,hE,EiA∼MKA(E)and hF,FiB∼MKB(F),KA(E)and KB(F)are also Noetherian.Furthermore,KA(E)and KB(F)are σ-unital and so are separable,by Lemma 2.8.Now if we assume that A is nuclear,then KA(E)is also nuclear,because we know that being nuclear is invariant under Morita equivalence of C∗-algebras(see[3],Proposition 3.2).Thus KA(E)⊗KB(F)is Noetherian,by Theorem 2.9(ii),But KA(E)⊗ KB(F)∼=KA⊗B(E ⊗ F)(see[21],Corollary 3.38).Therefore,KA⊗B(E ⊗ F)is Noetherian.Let H be a separable infinite-dimensional Hilbert space.In this case H is a Hilbert C-module and B a Hilbert B-module.Thus H⊗B∼=HBis Noetherian.

(ii)First,since E and F are full and Noetherian,A and B are also Noetherian,by Theorem 2.7.Thus A⊗B is Noetherian,by Theorem 2.9(ii).Furthermore,E⊗F is also Noetherian,by(i). ?

Proposition 2.13 Let E and F be Hilbert C∗-modules,respectively,over C∗-algebras A and B.If E is Noetherian and ϕ :A −→ LB(F)is a ∗-isomorphism,then E ⊗ϕF is also Noetherian.

Proof By assumption,KA(E)is Noetherian.But KA(E) ∼=KB(E ⊗ϕF)(see[14],Proposition 4.7),therefore,KB(E⊗ϕF)is Noetherian. ?

If we consider the example of C∗-algebras A and D,presented in the proof of Theorem 2.9(iii),as Hilbert C∗-modules,we conclude that being Noetherian as a Hilbert C∗-modules is not preserved under tensor product,in general.Of course,this property is always preserved under Morita equivalence of Hilbert C∗-modules and it passes to ideal submodules.

3 Properties of Projections

In this section we show that under certain conditions,we can attribute some of the properties of a simple C∗-algebra to Noetherian and Artinian C∗-algebras.As an application we obtain some properties of the C∗-algebra of compact operators of a Noetherian and Artinian Hilbert C∗-module.

Lemma 3.1 Suppose that the following conditions hold for properties X and Y in the category of C∗-algebras.

(i)Any simple C∗-algebra having property X,also as property Y.

(ii)Property X passes to closed ideals and quotients.

(iii)The property Y is preserved under extensions.

Then any Noetherian and Artinian C∗-algebra A having property X also has property Y.

Proof Since A is Noetherian,every non empty set of its closed ideals has a maximal element.Since A is both Noetherian and Artinian,it has composition series of closed ideals as 0=I0⊳I1⊳I2⊳···⊳In=A,such that Ij/Ij−1is simple,for each 1 ≤ j≤ n.By(ii),Ijand Ij/Ij−1have property X and so property Y0,by(i).In particular,A/In−1=In/In−1has the property Y.By(iii),A/In−2also has property Y because,the closed ideal In−1/In−2⊳A/In−2and the quotient(A/In−2)/(In−1/In−2) ∼=A/In−1have property Y.By continuing this process,A/I0∼=A has property Y. ?

We recall that the element a∈A is called full,if the closed ideal of A generated by a(i.e.,the smallest closed ideal containing a),is all of A.

Lemma 3.2 Let A be a Noetherian and Artinian C∗-algebra that has a full element a.Then either a is the only full element in A or there exists a neighborhood Nδ(a),with center a and radius δ>0,such that b is also full in A,for each b ∈ Nδ(a).

Proof Let

be a composition series of A.Then a ∈ AI(λ,n−1),(because if a belongs to a proper closed ideal in A,then the smallest closed ideal containing a is not A,which is a contradiction).Since I(λ,n−1)is closed,AI(λ,n−1)is open and so there is a neighborhood Nδλ(a),with center a and radius δλ>0,such that Nδλ(a) ⊆ AI(λ,n−1).Now suppose that{Sλ}λ∈Λis the set of all composition series in A and δ:=inf{δλ:λ ∈ Λ}.If δ=0,then a is the only full element in A,because if b is an element in A such that k a−b k> δ,then b must belong to a proper closed ideal in A and so it is not full.If δ>0,then there is the desired neighborhood Nδ(a). ?

A C∗-algebra A is said to have the ideal property,in short(IP),if projections in A separate closed ideals in A,i.e.,whenever I,J are closed ideals in A such that I*J,then there is a projection in in IJ,or equivalently if each of its closed ideals is generated(as an ideal)by its projections([19],Remark 2.1).Let a ∈ A+and ǫ>0.Then(a − ǫ)+:= ϕ(a),where ϕ :R+→ R+is given by ϕ(t)=max{(t− ǫ),0}([13],p.640).

Now we are ready to state the main theorem of this section.

Theorem 3.3 Let the C∗-algebra A be Noetherian and Artinian and also purely infinite.Let E be a Hilbert A-module.Then

(i)Every closed ideal in A is generated by a single projection and A has the ideal property.

(ii)KA(E)has a full projection,is purely infinite and has the ideal property.

Proof (i)Let I be a closed ideal in A.Then I is also Noetherian and Artinian,because being Noetherian and Artinian pass to closed ideals.First,we show that I is generated by a single positive element.Every simple C∗-algebra that is purely infinite,contains an infinite projection([4],Corollary V.2.3.1)that is full,by simplicity.Thus every purely infinite,simple C∗-algebra is generated(as a closed ideal)by a single positive element.Also,being purely infinite passes to closed ideals and quotients([13],Proposition 4.3).Furthermore,if the closed ideal J and the quotient I/J are generated(as closed ideals)by a single positive element and we consider the short exact sequence 0−→Jι−→Iπ−→I/J−→0,then by lifting the generator of I/J to I and adding the generator of J to it,we obtain a single generator for I.Thus I is generated by a single positive element a,by Lemma 3.1.We now consider two cases,by the previous lemma.If a is the only full positive element in I,then it is equivalent to a projection p in I,because I is purely infinite and so the positive element a is properly infinite.Thus p is full and so a=p by uniqueness.If there exists a neighbourhood Nδ(a)whose elements are also full in I,then since(a−ǫ0)+∈ Nδ(a),for an 0< ǫ0< δ,I is also generated by(a− ǫ0)+and so by a single projection,according to the argument in the implication(i)⇒(ii)in Proposition 2.7 of[19],(without needing to assumptions separability and(i)of that proposition and,of course,applying the previous lemma).Thus,every closed ideal in A is generated by a single projection.This implies that A has the ideal property.

(ii)This follows from(i),because being Noetherian and Artinian and being purely infinite pass to closed ideals and are preserved under Morita equivalence[13],and,moreover,we have hE,EiA∼MKA(E). ?

A C∗-algebra is said to be of type I(or postliminal,or GCR)if its image under every irreducible*-representation contains the compact operators(see[23],p.170).

Proposition 3.4 Let A be a Noetheian C∗-algebra and E be a countably generated Hilbert A-module.

(i)Every closed ideal in A corresponds to a compact-open subset of Prim(A).

(ii)If A is also separable and purely infinite,then every closed ideal in A is generated by a single projection and,in addition,KA(E)has a full projection,is purely infinite and has the ideal property.

(iii)If A is also separable and of type I,then KA(E)is a Noetherian AF-algebra.

Proof (i)Since Prim(A)is Noetherian,each open set in Prim(A)is compact and so each closed ideal in A corresponds to a compact-open subset of Prim(A),via I 7→{J ∈ Prim(A):I⊆J}c.

(ii)Every closed ideal in A is generated by a single projection,by(i)and Proposition 2.7 of[19]and so A has the ideal property.Since KA(E)is σ-unital,it is separable,by Lemma 2.8.Thus the last assertion holds.

(iii)Being of type I is preserved under Morita equivalence(see[23],p.170).Now,since KA(E)is Noetherian,separable and of type I,it is also an AF-algebra(see[5],p.80).

We know that if A ⊆ B is an inclusion of C∗-algebras with a faithful canonical conditional expectation E:B → A,then kxk=kE(x∗x)k is a norm induced by the inner product=E(x∗y)and so EE:=is a Hilbert A-module.A conditional expectation E:B → A is said to have finite index if there exists u1,u2,···,un∈ B such that[12,28].

We use the previous notation in the following theorem,which is the second main result of this section.

Theorem 3.5 Assume that A ⊆ B is an inclusion of C∗-algebras with a conditional expectation E:B→A that is faithful and of finite index.If A is Noetherian(resp.Artinian),then EEand LA(EE)are Noetherian(resp.Artinian).Furthermore,LA(EE)=B(EE).

Proof For any x∈EE=Bk.kE,there is a sequence(bm)m⊆B such that x= lim m→∞bm.But E is of finite index,thus there exists u1,u2,···,un∈ B such that for each m ≥ 1,

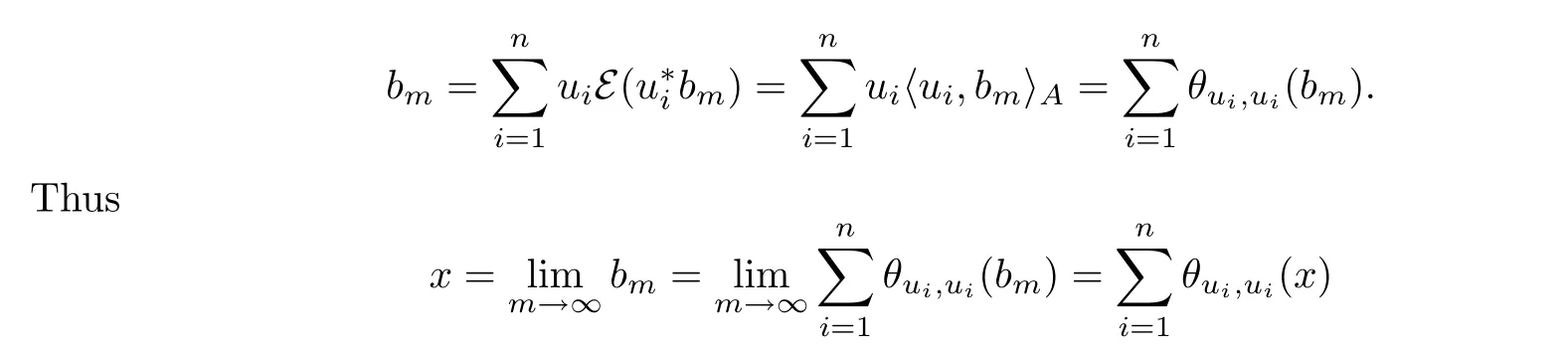
for each x∈EE.Thereforeis the identity operator and belongs to KA(EE).Now,let A be Noetherian(resp.Artinian).Sinceis a closed ideal in A,hEE,EEiA∼MKA(EE)and LA(EE)=M(KA(EE))=KA(EE),EEand LA(EE)are also Noetherian(resp.Artinian).Furthermore,since KA(EE)contains the identity operator,EEis self-dual(see[1],Lemma 3.3(i))and so LA(EE)=B(EE). ?

In particular,if A is finite-dimensional,then A,B and EEare Noetherian and Artinian.Because,we know that if E is of finite index,then A is finite-dimensional iff B is so(see[28],Lemma 2.7.1).Furthermore,since A is separable,KA(EE)is also separable,by Lemma 2.8.

In general,if a conditional expectation E:B→A is faithful and of finite index,A and B are not necessarily Morita equivalent.For example,the map E:M2(C)→C2,defined byis a faithful conditional expectation of finite index(see[27],Example 2.10).But M2(C)and C2are not Morita equivalent,because C2is non-simple.Of co urse,for a conditional expectation E:B→A,if(en)nis a countable approximate unit for B(i.e.,B is σ-unital)then(E(en))nis a countable approximate unit for A because

for each a ∈ A.Thus A is also σ-unital and so A ∼MB i ffA and B are stably isomorphic,by the Brown-Green-Rieffel theorem(see[21],Theorem 5.55).