A NOTE ON THE UNIQUENESS AND THE NON-DEGENERACY OF POSITIVE RADIAL SOLUTIONS FOR SEMILINEAR ELLIPTIC PROBLEMS AND ITS APPLICATION∗
2018-09-08ShinjiADACHI
Shinji ADACHI
Department of Mathematical and Systems Engineering,Faculty of Engineering,Shizuoka University,3-5-1 Johoku,Naka-ku,Hamamatsu 432-8561,Japan
E-mail:adachi@shizuoka.ac.jp
Masataka SHIBATA
Department of Mathematics,Tokyo Institute of Technology,2-12-1 Oh-okayama,Meguro-ku,Tokyo 152-8551,Japan
E-mail:shibata@math.titech.ac.jp
Tatsuya WATANABE
Department of Mathematics,Faculty of Science,Kyoto Sangyo University,Motoyama,Kamigamo,Kita-ku,Kyoto 603-8555,Japan
E-mail:tatsuw@cc.kyoto-su.ac.jp
Abstract In this paper,we are concerned with the uniqueness and the non-degeneracy of positive radial solutions for a class of semilinear elliptic equations.Using detailed ODE analysis,we extend previous results to cases where nonlinear terms may have sublinear growth.As an application,we obtain the uniqueness and the non-degeneracy of ground states for modified Schrödinger equations.
Key words positive radial solution;uniqueness;non-degeneracy;shooting method
1 Introduction and Main Results
In this paper,we consider the uniqueness and the non-degeneracy of positive radial solutions for the following semilinear elliptic problem

where N ≥2 and g:[0,∞)→R.Especially we are interested in the case where the nonlinear term g may have a sublinear growth at infinity.
Equation(1.1)appeared in various fields of mathematical physics and biology,and was studied widely.Particularly,almost optimal conditions for the existence of nontrivial solutions were obtained in[5,6,17].Equation(1.1)has the variational structure and solutions of(1.1)can be characterized as critical points of the functional E:H1(RN)→R defined by

There are lots of works concerning with the uniqueness of positive radial solutions for(1.1).See[10,20]for the model case g(u)= −u+u3or g(u)= −u+upand[4,18,22,23,25–27,29]and references therein for more general nonlinearities.But there still remains a gap between sufficient conditions for the existence and those for the uniqueness.Especially when the nonlinear term may have sublinear growth at infinity,the uniqueness is not known in general.
Once we could obtain the uniqueness of positive solutions of(1.1)and go back to its proof,we can also show that the unique positive solution of(1.1)is non-degenerate,that is,the linearized operator L= ∆+g′(u)has exactly N-dimensional kernel which is given by span(see also Corollary 2.4 below).This type of non-degeneracy can be applied in various ways.See for example[14,24]for singularly perturbed problems,[21]for the existence of traveling waves of nonlinear Schrödinger equations and[30]for the(in)stability of standing waves for nonlinear Schrödinger equations.
Our aim of this paper is to prove the uniqueness and the non-degeneracy of positive radial solutions of(1.1)for general nonlinearities to which previous results cannot be applied.Especially as we have mentioned above,we are interested in the case where the nonlinear term may have sublinear growth at infinity.
To state our main result,we impose the following conditions on the nonlinear term g:
(G1)g ∈ C1[0,∞),g(0)=0 and g′(0)<0.
(G3)There exists ζ>b such that G(ζ)=g(s)ds>0.
(G4)There exists s∗∈ (b,]such that Kg(s)is decreasing on(b,s∗)and Kg(s)>1 on(b,s∗).If s∗ (G5)Kg(s)≤1 on(0,b), here Kg(s)is the growth function of g(s)which is defined by Roughly speaking,the function Kgmeasures growth orders at zero and infinity.For example if g(s)= −s+sp,we can easily see that Kg(0)=1 and Kg(∞)=p.Especially when Kg(∞) ∈ (0,1),the nonlinear term g has sublinear growth at infinity.We also note that if b< ∞,then it follows that kukL∞ In this setting,we obtain the following result. Theorem 1.1 Assume(G1)–(G5).Then(1.1)has at most one positive radial solution.Moreover the corresponding linearized operator L= ∆ +g′(u)does not have 0-eigenvalue in As for the existence of a positive radial solution of(1.1),it suffices to assume(G1),(G3)and the following additional conditions(see[5,6,17]): Although the existence of a positive radial solution can be obtained under weaker assumptions,we don’t give precise statements here.By Theorem 1.1 and Corollary 2.4 below,we have the following result. Corollary 1.2 Assume(G1)–(G6).Then the positive radial solution of(1.1)is unique and non-degenerate. Now since we are interested in the positive radial solutions,(1.1)reduces to the following ordinary differential equation To obtain the uniqueness of positive radial solutions of(1.3),we apply the shooting method as in[20,22].More precisely,let us consider the initial value u(0)=d for d>0 and denote by R(d)the first zero of u=u(r,d).Then it suffices to show that there exists a unique d0>0 such that R(d0)= ∞.To this end,we consider the variation δ(r,d)=(r,d).As in[20,22],the key is to construct a suitable comparison function which has the same zero as δ.Although a general method based on I-theorem was established in[22],this method may fail if the nonlinear term has a sublinear growth at infinity.Thus our main purpose is the construction of the comparison function without using I-theorem(see also Remarks 2.6,3.7 below).Consequently,we are able to improve the result in[22]to obtain the non-degeneracy of the unique positive radial solution of(1.1). As an application of Theorem 1.1,we study the uniqueness and the non-degeneracy of ground states for the following modified Schrödinger equation where N≥2,λ>0,κ>0 and p>1.In Section 4,we will see that the quasilinear problem(1.4)can be transformed into a semilinear problem of form(1.1).Then by Theorem 1.1,two advances on previous results for(1.4)can be made:one is the uniqueness result for N=2 which was not studied in[3],and the other is the non-degeneracy result for 1 This paper is organized as follows.In Section 2,we classify the set of initial values as in[20,22]and prove Theorem 1.1,leaving the proof of the main proposition into Section 3.Section 3 is the most technical part and we will construct a suitable comparison function by using detailed ODE analysis.Finally in Section 4,we study the uniqueness of positive radial solutions for a class of quasilinear elliptic problems.Especially we will apply Theorem 1.1 to obtain a completely optimal result for the uniqueness and the non-degeneracy of complex valued ground states of modified Schrödinger equations in Subsection 4.4. In this section,we give some preliminaries and prove Theorem 1.1.To this end,we study the structure of radial solutions of the following ODE For d>0,we denote the unique solution of(2.1)by u(·,d).Then as in[20]and[22],we can classify the sets of initial values as follows When d ∈ N,we may assume that R(d)is a first zero of u(r,d).Then it follows that u′(R)<0.Furthermore when d∈G,we set R(d)=∞.In this setting,we have the following result. Proposition 2.1 We obtain the following properties. (i)The sets N,G and P are disjoint,N ∪P ∪G=(0,b)and(0,b]⊂ P.Especially if u is a solution of(1.3),then u(0)>b.Furthermore N and P are both open in(0,b). (ii)If d∈N∪G,then the corresponding solution u(r,d)of(2.1)is monotone decreasing with respect to r. (iii)If d∈G,then u(k)(r,d),k=0,1,2 decay exponentially at infinity.Moreover it follows that Next in order to study the uniqueness and the non-degeneracy of the positive radial solution of(2.1),we consider the following linearized problem For a solution u=u(·,d)of(2.1),we denote the unique solution of(2.3)by δ(·,d)and sometimes we denote it by δ(·)for simplicity.Our first purpose is to establish the following result. Proposition 2.2 Suppose(G1)–(G4)hold. (i)If d ∈ G,then δ(r,d)has at least one zero in(0,∞). (ii)Let d0=inf(N ∪ G).Then d0∈ G and δ(r,d0)has exactly one zero rδ∈ (0,∞).Moreover it follows that (iii)Let d ∈ G and suppose that δ(r)→ −∞ as r→ ∞.Then there exists ε>0 such that(d,d+ ε)⊂ N and(d− ε,d)⊂ P. Proof When b< ∞,the proof can be found in[25].Thus it suffices to consider the case b=∞. To prove(i),we suppose by contradiction that δ(r,d)>0 on(0,∞).First differentiating(2.1),we have Then by a direct calculation,we obtain the following Picone identity Integrating it over(r,r)for any(r,r)⊂(0,∞),we get Now since both u and u′decay exponentially at infinity,also decays exponentially.Moreover it follows that either δ),δ′()→0 or δ(),δ′()→ ∞as→ ∞(see[22]Lemma 2(b)for the proof).In the former case,δ,δ′decay exponentially and δ′/δ→pas→∞.In the latter case,we also have δ′()/δ(r)>0 for larger.Thus in both cases,we obtain On the other hand since δ(0)=1,δ′(0)=0 and u′(0)=0,we have from(2.1)that Thus it follows that This is a contradiction and hence δ has at least one zero. Finally proofs of(ii)and(iii)can be done by similar arguments in[22]Lemmas 3(b)and 10. ? We note that if δ(r,d)has exactly one zero in(0,R)for d ∈ N ∪ G,then d is called admissible.Moreover if d is admissible,and δ(R,d)<0 for d ∈ N or δ(r) → −∞ as r → ∞for d∈G,then d is said to be strictly admissible(see[20]and[22]).Our goal is to prove the following result which shows the strict admissibility of any admissible d∈N∪G.We will give its proof in Section 3. Proposition 2.3 Assume(G1)–(G5)and let d ∈ N ∪ G.Suppose further that δ(r,d)has exactly one zero in(0,R).Then it follows that δ(R,d)<0 for d ∈ N or= −∞ for d∈G. Now we are ready to prove Theorem 1.1. Proof of Theorem 1.1 First we prove the uniqueness.To this end,we suppose by contradiction that problem(1.3)has at least two positive radial solutions.Especially one has G 6=∅. Now by Proposition 2.2(ii),d0=inf(N∪G)∈G is admissible and hence d0is strictly admissible by Proposition 2.3.Thus by Proposition 2.2(iii),there exists ε>0 such that Moreover taking ε smaller if necessary,we may assume that d ∈ (d0,d0+ε)is admissible.In fact since d0is strictly admissible,it follows that δ(r0,d0)<0,δ′(r0,d0)<0 andfor sufficiently large r0>0.Thus for d sufficiently close to d0,δ(r,d)has exactly one zero on(0,r0],δ(r0,d)<0,δ′(r0,d)<0 and g′?u(r,d)?<0 for r ∈ (r0,R(d)).If δ(r)= δ(r,d)has a zero r1∈ (r0,R(d)),then δ has a negative minimum at r2∈ (r0,r1)and hence This is a contradiction.Thus d ∈ (d0,d0+ε)is admissible,that is,δ(r,d)has exactly one zero on(0,R(d))for any d∈(d0,d0+ε). Next since we assumed that the set G has at least two elements,we have(d0,) ∩ G 6= ∅and hence we can define Then from(2.4),it follows that d1>d0.Moreover by the definition,we can see that(d0,d1)⊂N.Finally since N and P are open by Proposition 2.1(i),we also have d1∈G.Especially by Proposition 2.2(i),δ(r,d1)has at least one zero on(0,R). Let N(d)be the number of zeros of δ(r,d)on(0,R(d)).Next we claim that N(d) ≤ 1 for d∈(d0,d1)⊂N.Indeed we know that N(d)=1 for any d∈(d0,d0+ε).Moreover by the continuity of zeros of δ(r,d)with respect to d,N(d)changes only one by one as d increases.Especially by Proposition 2.3,it cannot happen that N(d)increases from 1 to 2,otherwise such a d∈(d0,d1)is admissible but not strictly admissible.This implies that N(d)≤1 for any d∈(d0,d1). Now suppose that δ(r,d1)has exactly one zero.Then by Proposition 2.3,it follows that d1is strictly admissible and hence(d1− ε′,d1) ⊂ P for some ε′>0 by Proposition 2.2(iii).But this contradicts to the definition of d1.Next we suppose that δ(r,d1)has at least two zeros.Since zeros of δ(r,d)depend continuously on d,we have N(d) ≥ 2 for d Finally,let L= ∆ +g′(u):H2(RN) → L2(RN)be the linearized operator around u,and suppose that ϕ0is a nontrivial radial eigenfunction corresponding to 0-eigenvalue of L,that is, Since ϕ0and δ satisfy the same initial condition at the origin, ϕ0is a constant multiple of δ.Then by Proposition 2.3,we have ϕ0→ −∞ as r → ∞ and hence ϕ06∈(RN).This completes the proof. ? Once we could obtain the uniqueness of the positive radial solution,one can show more precise information on the spectrum of L.Indeed we can prove the following result. Corollary 2.4 Assume(G1)–(G6)and let L= ∆ +g′(u)be the linearized operator around the unique positive radial solution u of(1.1).Then the following properties hold. (i) σ(L)= σp(L)∪σe(L),where σp(L)and σe(L)are the point spectrum and the essential spectrum of L respectively. (ii) σe(L)=(−∞,g′(0)]and σp(L) ⊂ (g′(0),∞). (iii)Ifµ ∈ σp(L),then the corresponding eigenfunction ϕ(x)satisfies for any small ε>0 and some Cǫ>0. (iv)Ifµ∈σp(L)∩(0,∞),then the corresponding eigenfunction is radially symmetric. (v)The principal eigenvalue µ1(L)>0 is simple,and the corresponding eigenfunction ϕ can be chosen to be positive. (vi)The second eigenvalueµ2(L)is zero,and the eigenspace associated with the eigenvalueµ=0 is spanned by Proof The proof can be done in a similar way as in[4,Theorem 5.4,P.259].Thus we omit the proof. ? Now we give some preliminaries to prove Proposition 2.3.For s>0 and λ>0,we define the I-function by We note by the definition of Kg(s)that Lemma 2.5 Assume(G1)–(G5). (i)For each t∈ (b,s∗),there exists a unique Λ(t)>0 such that Moreover the map t 7→ Λ(t)is continuous. (iii)If s∗<,then I(s,λ)<0 for all s ∈ [s∗,)and λ >0. Proof (i)First we claim that I(s,λ)>0 for 0 Next by(G4),Kg(s)is decreasing on(b,s∗)and Kg(t)>1 for t∈ (b,s∗).Thus there exists a unique λ>0 such that Kg(t)=1+.Putting Λ(t)=,(i)holds. (iii)Let s ∈ [s∗,b).Then one has from(G4)that Kg(s) ≤ 1 and>1.Thus from(2.5),the claim follows.? Remark 2.6 Ifb=s∗= ∞,Lemma 2.5(i)shows that I-theorem in[22]holds(see[22,Theorem 1]).Then Proposition 2.3 follows from Lemma 8 in[22]. In this section,we prove Proposition 2.3.To this end,let d ∈ N∪G and assume that δ(r,d)has exactly one zero in(0,R).Furthermore we suppose by contradiction that δ(R)=0 when d ∈ N and δ(r)stays bounded at infinity when d ∈ G.Then by Proposition 2.2 and from(2.2),we can show that δ′(R)>0 if d ∈ N and δ(r) → 0 exponentially as r → ∞ if d ∈ G(see[22,Lemma 2,p.497]). To derive a contradiction,we define We note that vλ(0)= λu(0)>0.Moreover one can see that vλsatisfies Our aim is to compare δ with vλ,and our goal is to show the following lemma. Lemma 3.1(Key lemma) Let rδ∈ (0,R)be the unique zero of δ(r,d).Then there exists λ0>0 such that As we will see later,we can prove Proposition 2.3 by Lemma 3.1(see also Remark 3.7 below).The proof of Lemma 3.1 consists of several lemmas. Lemma 3.2 Let λ>0.Then we obtain the following properties. (i) For sufficiently large r>0,it follows that vλ(r)<0(vλ(R)<0 when R< ∞).Especially vλhas a zero on(0,R). (ii)For sufficiently large λ >0,vλdoes not have any zeros on[0,rδ].Especially it follows that vλ>0 on[0,rδ]. Proof (i)First we consider the case d∈G.By the definition of vλand from(2.2),one has Since vλis continuous and vλ(0)>0,the claim holds.When d ∈ N,the claim also follows from vλ(R)=Ru′(R)<0. (ii)By the definition of vλ,it follows that Thus the r.h.s of(3.3)is positive for sufficiently large λ. ? Lemma 3.3 Let rδbe the unique zero of δ(r)and suppose that δ(r)→ 0 as r → R.Then it follows that b Proof First we show that b Integrating(3.4)over[rδ,r]and using the integration by parts,we get Now suppose that d ∈ G.Then since u,u′and δ decay exponentially as r → ∞,we can pass the limit r→∞to obtain However since g(u)<0 and δ<0 on(rδ,∞),this is a contradiction.Next let d ∈ N.In this case,one has u(R)=0,u′(R)<0,δ(R)=0 and δ′(R)>0.Taking r=R,we get This is a contradiction again and hence b Next we prove u(rδ) Moreover taking large λ >0,we have by Lemma 3.2(ii)that vλ>0 on(0,rδ).Thus we obtain From(2.3),(3.2)and δ(rδ)=0,we can apply the Sturm Comparison Principle(Lemma A.1(b)below)to show that vλhas a zero on(0,rδ).This contradicts to Lemma 3.2(ii)and hence the claim holds. ? Now by Lemma 3.3,we can apply Lemma 2.5(i)with t=u(rδ).Putting λ = Λ?u(rδ)?,we get Then by Lemma 2.5(ii)and the continuity of u,we also have Finally since u is decreasing,we obtain Next we investigate the sign of vλnear its zero. Lemma 3.4 We obtain the following properties. (i) Let λ ≥ λ and suppose that vλhas a zero r0∈ (rδ,R).Then it follows that either(r0)0,or(r0)=0 and(r0)>0.In other words,if vλis negative before r0,then vλmust be positive after r0. (ii)Suppose that vλhas a zero r0∈(0,rδ).Then it follows that either(r0)6=0,or(r0)=0 andr0)<0.In other words,ifis positive before r0,then vλmust be negative after r0. Proof Assume that vλ(r0)=0 and(r0)=0 for some r0∈(rδ,R).Then from(3.1)and(3.5),one has Thus the claim holds.(ii)can be shown in a similar way. ? Lemma 3.5 Let λ ≥ λ.Then vλhas at most one zero on(rδ,R).More precisely if vλhas a zero r0∈ (rδ,R),then it follows that Proof First we prove the following claim. Indeed suppose by contradiction that vλ(r)>0 for r>nearThen by Lemma 3.2(i),vλhas a next zero∈(,R)and vλ>0 on().Thus from(3.5),one has In this case,we can apply Lemma A.1(a)to conclude that δ must have a zero on(ˆr0, r0)⊂(rδ,R).This contradicts to the assumption which we made in the beginning of this section and hence the claim holds. Now we assume that there exists r0∈ (rδ,R)such that vλ(r0)=0.Then by the claim above,it follows that vλ<0 on a right neighborhood of r0.Moreover if vλhas a next zero r1>r0,then vλmust change its sign from negative to positive by Lemma 3.4(i).This contradicts to the above claim provided=r1and hence Next we observe from(3.6)and by Lemma 3.4(i)that vλ>0 on a left neighborhood of r0.If there exists r2∈ (rδ,r0)such that vλ(r2)=0,it follows that vλ>0 on(r2,r0)⊂ (rδ,R).Then by applying the above claim withˆr=r2,we obtain a contradiction.This implies that vλ>0 on(rδ,r0)andr0)<0.? Lemma 3.6 vλhas a unique zero r ∈ (0,rδ),that is, Proof First we show that vλhas at least one zero on(0,rδ).Indeed if vλ>0 on(0,rδ),we have from(3.5)that Then by Lemma A.1(b),vλmust have a zero on(0,rδ).This is a contradiction and hence the existence of a zero r ∈ (0,rδ)holds.Moreover we may assume that r is the first zero of vλ. Now by Lemma 3.4(ii),vλ<0 on a right neighborhood of r.If vλhas a next zero r1∈ (r,rδ],it follows that vλ<0 on(r,r1).From(3.5),we get Then by Lemma A.1(a),δ must have a zero on(r,r1).This contradicts to the assumption of Proposition 2.3 and hence vλ<0 on(r,rδ].In this case,vλcannot have a zero on(rδ,R)by Lemma 3.5.This completes the proof. ? Now by Lemma 3.2(ii),we can choose large λ > λ so that vλ>0 on[0,rδ].Then by Lemmas 3.2(i)and 3.5,vλhas a unique zero r ∈ (rδ,R). To prove the key lemma,we define as in[20].Then one has Now we are ready to prove the key lemma. Proof of Lemma 3.1 From(3.7),(3.8)and by Lemma 3.5,it follows that Moreover by Lemma 3.6,we also have Next we claim that θ′>0 on(rδ,r].Indeed suppose by contradiction that θ′(ˆr)=0 for someˆr∈(rδ,r).Puttingˆλ:=θ(ˆr),it follows from(3.7)that vˆλ(ˆr)=0.Moreover since>rδ>r,we have from(3.10)that>λ.Thus by Lemma 3.5,we get<0 and hence>0 from(3.8).This is a contradiction and the claim holds. Now from(3.9),(3.10)and θ′>0 on(rδ,],it follows that Putting λ0:= θ(rδ),we have from(3.7)that This implies that vλ0>0 on a right neighborhood of rδ,which contradicts to the fact vλ0<0 on(rδ,R).Thus we obtain(rδ)<0. Finally we prove Proposition 2.3 by using Lemma 3.1. Proof of Proposition 2.3 As we have mentioned in the beginning of this section,we assume that δ(r,d)has exactly one zero rδ∈ (0,R)and suppose by contradiction that δ(R)=0 when d ∈ N and δ(r)stays bounded at infinity when d ∈ G.Then it follows that δ(r) → 0 exponentially as r→∞if d∈G. First we suppose that d∈N.In this case,one has by Lemma 3.1 and(3.5)that Since δ(rδ)= δ(R)=0,we can apply Lemma A.1 to show that vλ0has a zero on(rδ,R).But this contradicts to Lemma 3.1. Next we consider the case d∈G.We put Then from(3.5)and by Lemma 3.1,one has ϕ < ψ on(rδ,∞).Moreover since vλ06=0 on(rδ,∞),we can rewrite(2.3)and(3.2)as respectively.By a direct computation,one can obtain the following Picone identity holds: Integrating it over[r,t]⊂ (rδ,∞),we get Next from(2.1),(2.2)and by the definition of vλ0,it follows that Since δ decays exponentially at infinity,we have Moreover since δ(rδ)=0 and vλ0(rδ)=0,we can apply l’Hˆopital’s rule to obtain Thus we also have Now from(3.11),(3.12)and(3.13),it follows that This is a contradiction because ϕ < ψ on(rδ,∞)and hence the proof is completed. ? Remark 3.7 As we have noted in Remark 2.6,we can obtain Proposition 2.3 by the previous result in[22]when Kg(∞)≥ 1.Actually the key of the proof of the strict admissibility was to construct a comparison function vλhaving the same zero with δ.In[22],this construction was done by applying the I-theorem.Our argument shows that we can construct such vλwithout using the I-theorem. We also observe that Kg(∞)≥ 1 is equivalent to the fact that g(s)has superlinear or asymptotically linear growth at infinity.Since we were able to obtain Proposition 2.3 even if Kg(∞)<1,our result can cover the case where the nonlinearity may have sublinear growth or may be negative at infinity. In this section,we study the uniqueness of positive radial solutions for the quasilinear elliptic problem of the form: As an application,we will also show the uniqueness and the non-degeneracy of ground states for modified Schrödinger equations in Subsection 4.4. We impose the following conditions on the nonlinear term h(t)and the quasilinear term a(t). here Khand Kaare the growth functions of h and a respectively,which are defined in(1.2).We observe that if Ka(t)is non-decreasing on[0,∞),then(A3)automatically holds. A typical example of a(t)is given by a(t)=1+ κ|t|ℓfor κ >0 and ℓ≥ 2.Moreover by direct computations,we can see that a(t)=1+|t|ℓ1+|t|ℓ2for 0< ℓ1< ℓ2or a(t)=|t|2+e−ct2for 0 •Power nonlinearity: •Defocusing cubic-focusing quintic nonlinearity: •Focusing cubic-defocusing quintic nonlinearity: •Nagumo type nonlinearity: By elementary calculations,one can show that these nonlinearities fulfill(H1)–(H5).Similar statements also hold for quadratic-cubic nonlinearities h(t)= −t±c|t|t∓|t|2t. In this setting,we obtain the following result. Theorem 4.1 Assume(A1)–(A4)and(H1)–(H5).Then(4.1)has a unique positive radial solution u∈C2(RN).Moreover let L:H2(RN)→L2(RN)be the linearized operator of(4.1)which is given by In this subsection,we introduce a dual approach of(4.1)and prepare some auxiliary lemmas. To this aim,let f(s)be a unique solution of the following ODE From(A1),we can see that f is well-defined and f∈C2[0,∞).We also extend f(s)as an odd function for s<0.Then we have the following. Lemma 4.2 f(s)satisfies the following properties. (i)f>0 and f′>0 on(0,∞).Especially f is monotone on(0,∞)and hence the inverse f−1exists. Proof (i)and(ii)follow from(4.2).Moreover from(A4),we can show that(iii)holds(for the proof,we refer to[16]). ? Now we consider the following semilinear elliptic problem which we call a dual problem of(4.1).We also define the linearized operator L:H2(RN)→L2(RN)of(4.3)by Then we have the following relation between(4.1)and(4.3). Lemma 4.3 Let X={u∈H1(RN);a(u)|∇u|2∈L1(RN)}. (i) u∈ X∩C2(RN)is a positive radial solution of(4.1)if and only if v=f−1(u)∈H1∩C2(RN)is a positive radial solution of(4.3). Let u∈X∩C2(RN)is a positive solution of(4.1)and put v=f−1(u).Then (v)u is non-degenerate if and only if v is non-degenerate. For the proof of(i),we refer to[16].The proof of(ii)–(v)can be found in[3](see also[2,Lemmas 2.7 and 2.8]).By Lemma 4.3,it suffices to study the uniqueness and the nondegeneracy of positive radial solutions of(4.3). Remark 4.4 Let us consider the most typical case Then by Lemma 4.2(iii),we can see thatsatisfies for some C>0.This implies that if 1 In this subsection,we prove the existence of a positive radial solution u∈C2(RN)of(4.1).To this end,we show that the function satisfies(G1),(G3)and(G6)in Section 1.For s<0,we extend g(s)as an odd function. First we can easily see that g∈C1[0,∞).Moreover since h(0)=0 and f(0)=0,we also have g(0)=0.Next one has and hence(G1)holds. To prove(G3),we observe that Finally we show that(G6)holds.When N≥3,we have by(H5)and Lemma 4.2(iii)that Next suppose that N=2.By Lemma 4.2(iii),there exists C>0 such that f(s)ℓ+2≤ Cs2for large s>0.Moreover by the definition of f(s)and(A1),putting a:=a(t)>0,we also have f′(s)≤Thus from(H5),we obtain Now since(G1),(G3)and(G6)are satisfied,we can apply results in[5,6,17]to obtain the existence of a positive radial solution v∈H1∩C2(RN)of(4.3).Then by Lemma 4.3,we obtain the existence of a positive radial solution u∈X∩C2(RN)of(4.1). Finally we note that a positive radial solution of(4.1)obtained here is indeed a ground state of(4.1).To be more precise,we define the energy functional J:X→R by Moreover one can also show that w is positive and radially symmetric. In this subsection,we complete the proof of Theorem 4.1.By Theorem 1.1 and Lemma 4.3,it suffices to prove that(G1)–(G5)in Section 1 hold for Since we establish(G1)and(G3)in Subsection 4.2,it remains to show that(G2),(G4)and(G5)hold.To this end,let β,β>0 be constants in(H2)and define b:=f−1(β),b:=f−1(β),respectively. Lemma 4.5 The function g(s)defined in(4.4)satisfies(G2). Proof First we observe that g and h have same sign because f′>0.Thus from(H2),it follows that g(s)<0 for 0 Thus from(A1)and(H2),we obtain In a similar way,we can show that g(s)<0 on(b,∞)and g′(b)<0 when b< ∞.This completes the proof. ? In order to prove(G4)and(G5),we prepare the following lemma. Proof For simplicity,we put Then from(A1),it follows that φ ∈ C1[β,∞).Thus it suffices to show that φ′(t)≥ 0 on[β,∞). Now by a direct computation,one has Noticing that t≥ β,we have from(A3)that This implies that φ′≥ 0 on[β,∞)and hence the proof is completed. ? Lemma 4.7 The function g(s)defined in(4.4)satisfies(G4)and(G5). Proof First by the definition of Kg(s),Lemma 4.2(ii)and from(4.5),it follows that Since f(b)=β,we have only to show that is decreasing on[β,β).Now we can see thatKg(t)is rewritten as Thus from(A3),(H4)and by Lemma 4.6,the numerator is decreasing and the denominator is non-decreasing.So,(t)is positive and decreasing onthere existssuch that(t)is decreasing on[β,t]and(t)≤0 onIn either case,(G4)is satisfied. Next to prove(G5),it suffices to show that≤1 on(0,β).From(A1),(A2)and(H4),we have Thus(G5)holds.This completes the proof. In this subsection,we consider a special case a(t)=1+2κ|t|2,h(t)=|t|p−1t−λt,and study the uniqueness and the non-degeneracy of a complex-valued ground state,which are important in the study of the corresponding time-evolution Schrödinger equation. We consider the following modified Schrödinger equation where κ>0,p>1 and z:R×RN→C.For physical backgrounds,we refer to[7,19].We are interested in standing waves of the form:z(t,x)=u(x)eiλt,where λ >0 and u:RN→ C.Then we obtain the following quasilinear elliptic problem From physical as well as mathematical points of view,the most important issue is the stability of the standing wave.It is known that in the study of the stability of standing waves,the uniqueness and the non-degeneracy of ground states of(4.6)plays an important role(see[9,11,12]for results on the(in)stability of standing waves). Now we define the energy functional and the energy space by A solution w of(4.6)is said to be a ground state if it satisfies As for the existence and properties of a complex-valued ground state,we have the following.For the proof,we refer to[11]. Proposition 4.8 Suppose λ >0,κ >0 andThen problem(4.6)has a ground state w,which has a form w(x)=eiθ|w(x)|for some θ∈ R. Moreover let w be a real-valued ground state of(4.6).Then w satisfies the following properties (i)w∈C2(RN)and w(x)>0 for all x∈RN. (ii)w is radially symmetric and decreasing with respect to r=|x|. (iii)There exist c,c′>0 such that Proposition 4.8 tells us that up to a phase shift,we may assume that the ground state of(4.6)is real-valued.Moreover any ground states are positive and radially symmetric.Thus the uniqueness of the ground state of(4.6)follows from Theorem 4.1.Finally it is known that p=is the critical exponent for the existence of non-trivial solutions of(4.6).This can be proved by using the Pohozaev type identity(see[1]for the proof). Now let G be the set of ground states of(4.6).Since(4.6)is invariant under the translation and the phase shift,we have the following result. Theorem 4.9 Suppose that λ >0,κ >0 andLet w be the unique(real-valued)ground state of(4.6).Then we have Moreover we also have here L is the linearized operator of(4.6)around the unique(real-valued)ground state w,which is given by where φ is a complex conjugate of φ. Proof To prove Theorem 4.9,we put φ = φ1+iφ2with φ1,φ2∈ H2(RN,R)and decompose L into two operators L1,L2acting on φ1and φ2,respectively.By a direct computation,we have By Corollary 2.4,Lemma 4.3 and Theorem 4.1,it follows that Next we show that Ker(L2)=span{w}.Although the proof can be found in[28],we give a much simpler proof based on Corollary 2.4.By the definition of L2,one has w∈Ker(L2).We suppose by contradiction that there existsw∈H1(RN)such thatw 6≡w and L2(w)=0.This implies that 0 is not a simple eigenvalue of L2.Then by Corollary 2.4(v),it follows that the principal eigenvalue µ(L2)is negative and the corresponding eigenfunction ψ can be chosen to be positive. Since ψ satisfies multiplying(4.8)by w and integrating over RN,we get On the other hand,multiplying(4.6)with u=w by ψ,we also have Subtracting these equations,we obtain However sinceµ<0,ψ>0 and w>0,this is a contradiction.This implies that Ker(L2)=span{w}.This completes the proof of Theorem 4.9. ? Remark 4.10 In[3]and[28],the authors required a technical assumption 3≤p to obtain the non-degeneracy of the ground state of(4.6).We could remove this additional assumption in Theorem 4.9.The key is to obtain Proposition 2.3 even when the nonlinear term may have a sublinear growth. We also note that our result covers the case N=2.In[1],the uniqueness for the case N=2 is obtained under the assumption 3 ≤ p and some largeness condition on λ and κ.Theorem 4.9 enables us to obtain the uniqueness without any restrictions on κ,λ and p. Finally by Corollary 2.4,we can obtain more precise information on the linearized operator around the unique real-valued ground state.Indeed let L1be the linearized operator defined in(4.7).Then we have the following results,which answer the question raised in[1,Remark 5.6]and complete previous results on the non-degeneracy in[3,28]. (i) σ(L1)= σp(L1)∪ σe(L1),σe(L1)=[λ,∞)and σp(L1)⊂ (−∞,λ). (ii)Ifµ ∈ σp(L1),then the corresponding eigenfunction ϕ(x)satisfies for any small ε >0 and some Cǫ>0. (iii)Ifµ ∈ σp(L1)∩(−∞,0),then the corresponding eigenfunction is radially symmetric. (iv)The principal eigenvalueµ1(L1)<0 is simple,and the corresponding eigenfunction ϕ1can be chosen to be positive. (v)The second eigenvalueµ2(L1)is zero and Ker(L1)=span respectively on some interval(µ,ν) ⊂ [0,∞).Suppose that g and G are continuous,G ≥ g and G 6≡ g on(µ,ν).Assume further that one of the following conditions holds (a) µ >0 and U(µ)=U(ν)=0. (b) µ =0 and U′(µ)=V′(µ)=U(ν)=0. Then V has at least one zero on(µ,ν).
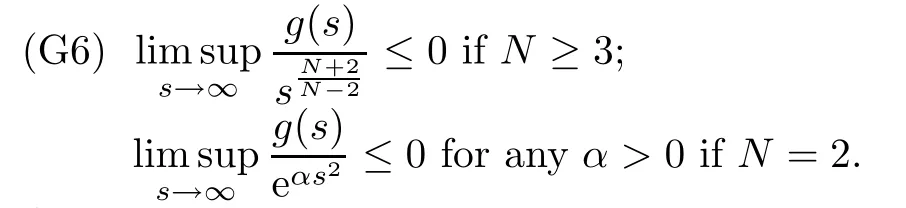


2 Classification of the Set of Initial Values and Preliminaries



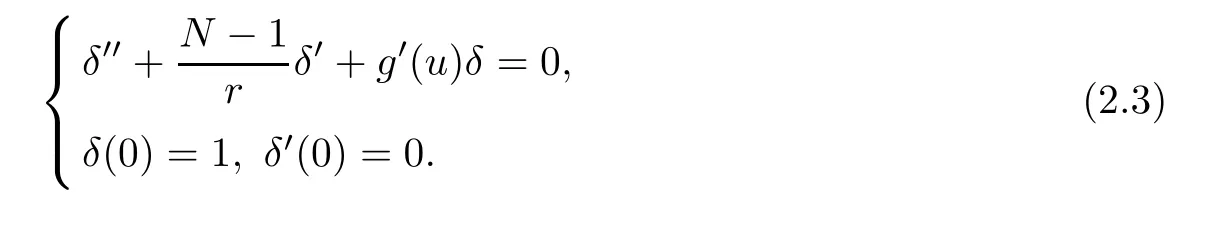









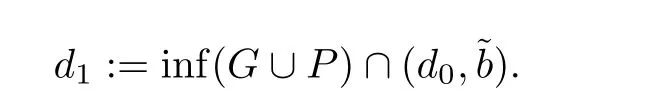
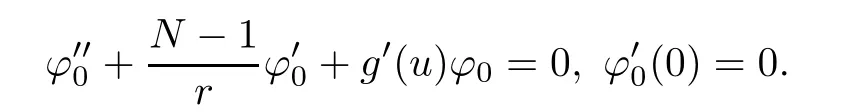

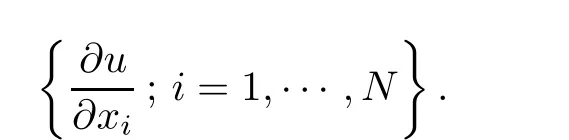





3 Proof of the Strict Admissibility



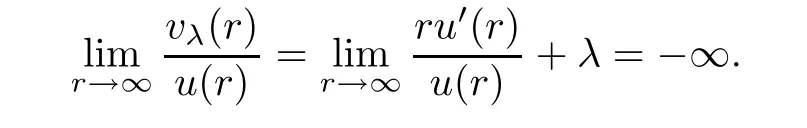

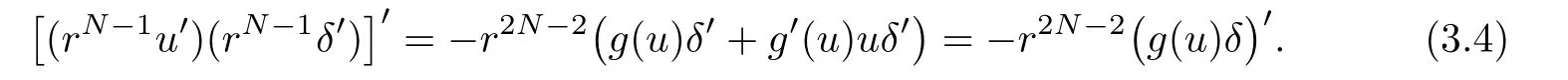

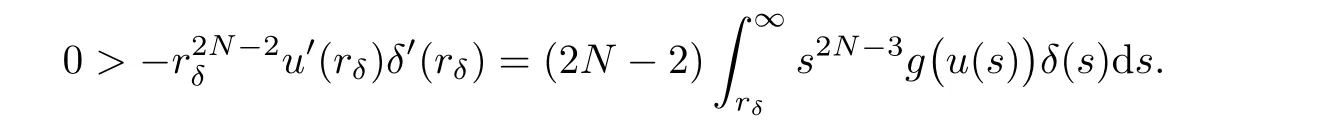

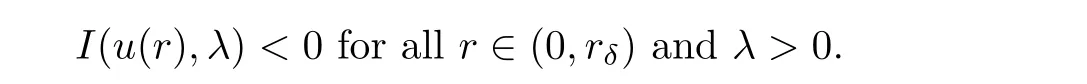


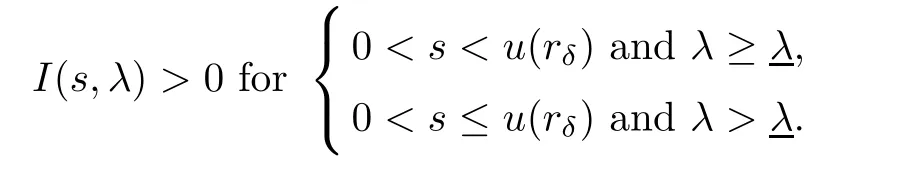

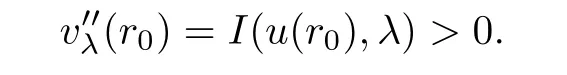












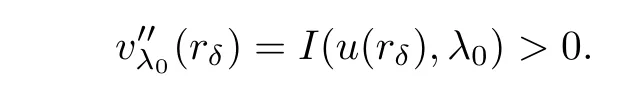
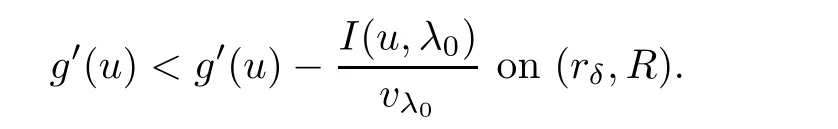

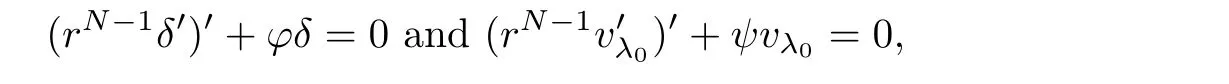






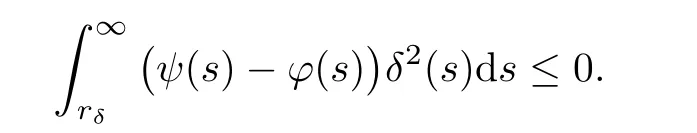
4 Application to Ground States of Modified Schrödinger Equations








4.1 Dual Approach and Auxiliary Lemmas
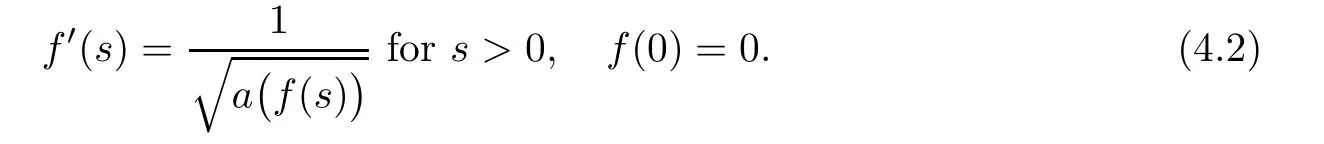
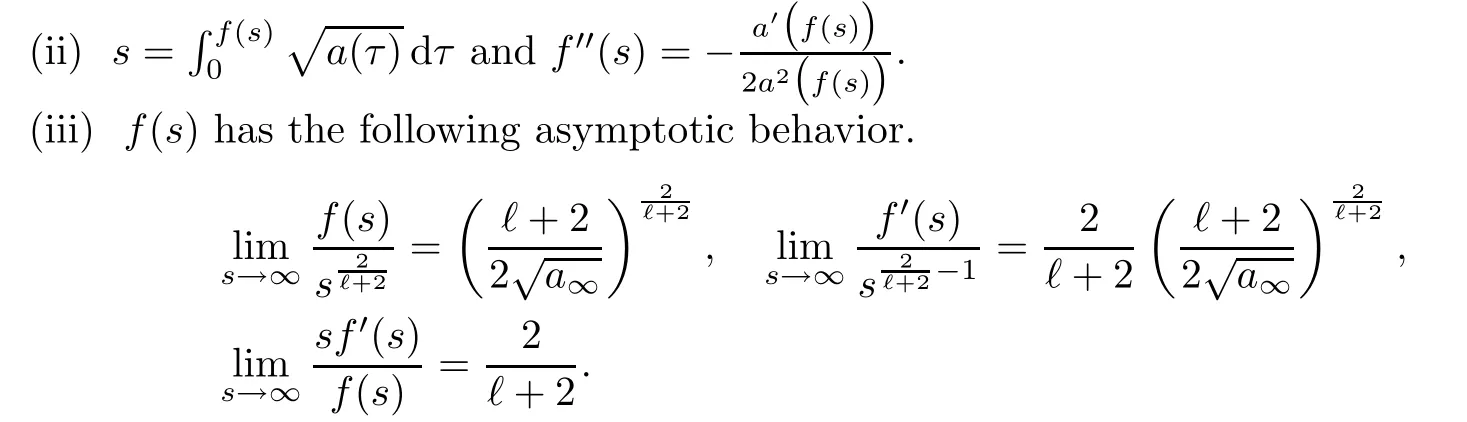


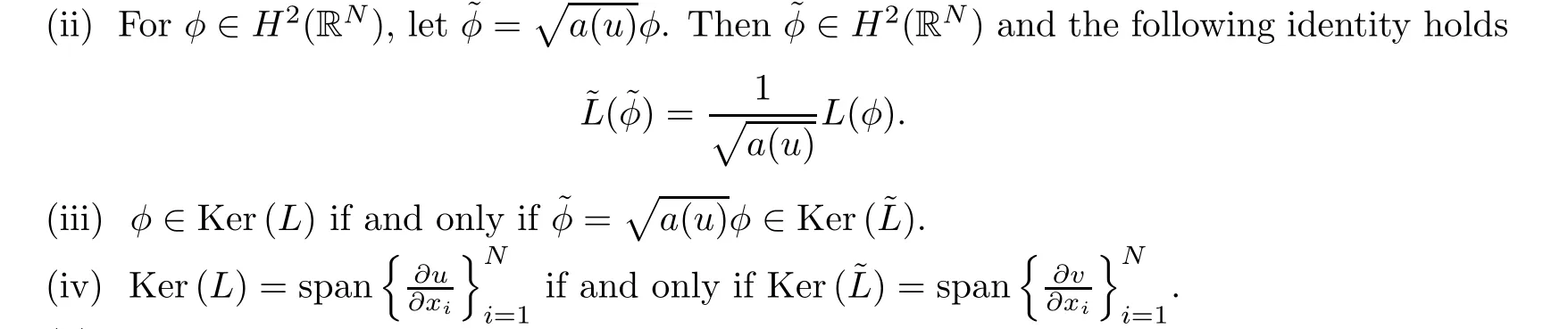

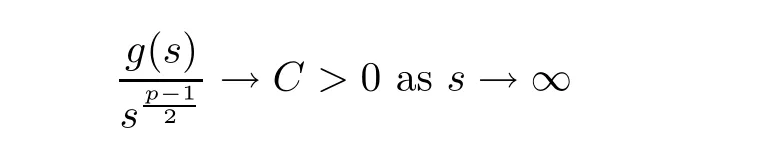
4.2 Existence of a Positive Radial Solution of(4.1)







4.3 Proof of Theorem 4.1





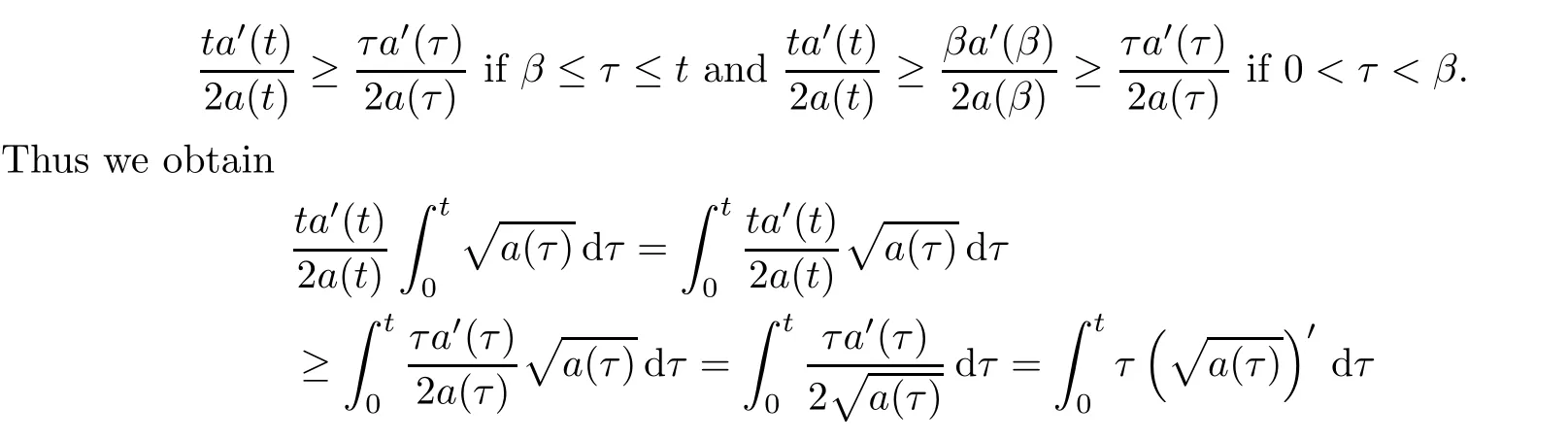
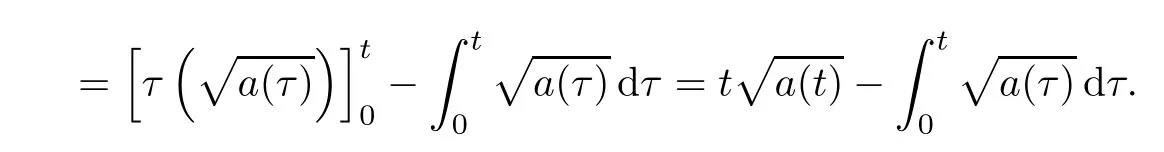
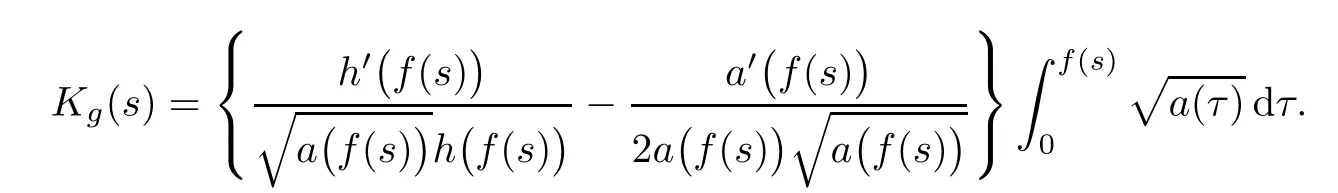
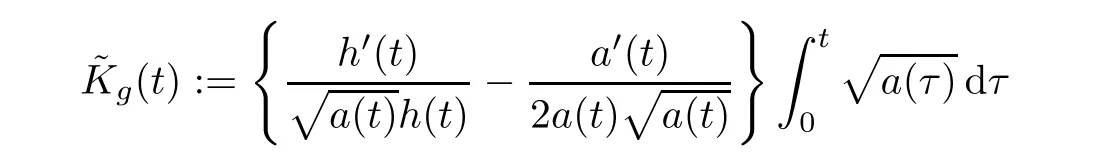


4.4 Results for the Complex Valued Ground State for Modified Schrödinger Equation


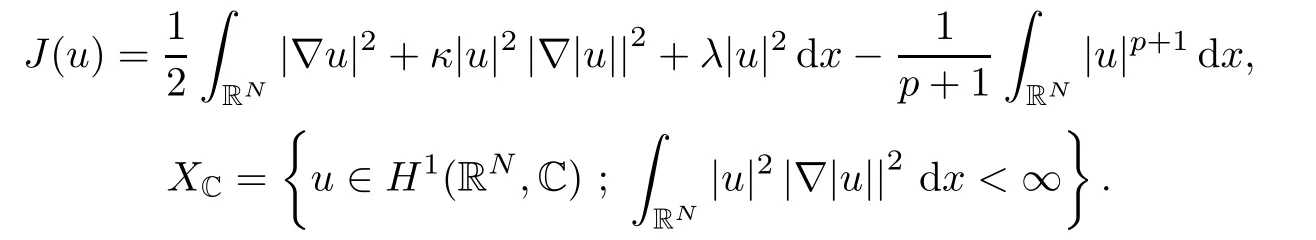


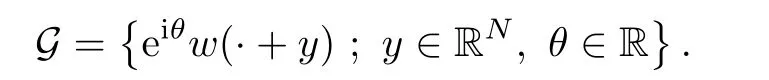

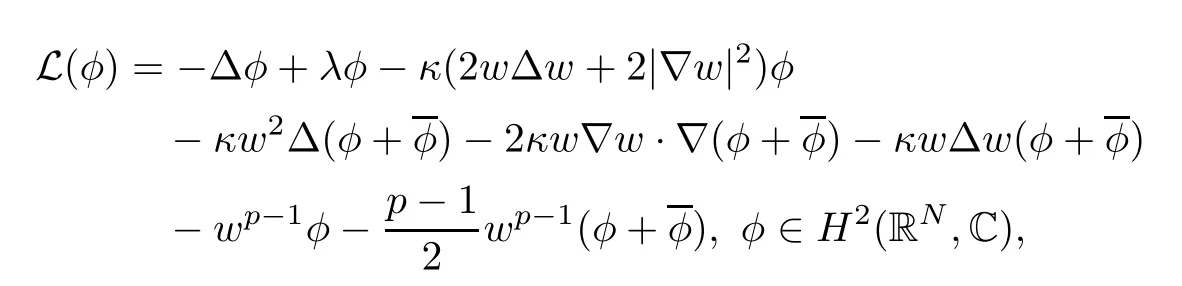


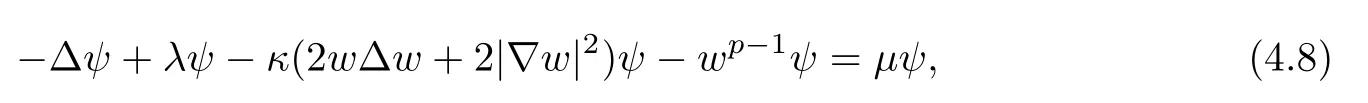


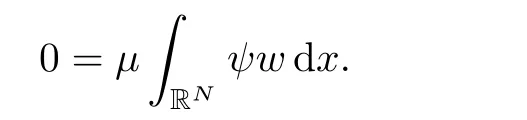


杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- PRODUCTS OF WEIGHTED COMPOSITION AND DIFFERENTIATION OPERATORS INTO WEIGHTED ZYGMUND AND BLOCH SPACES∗
- SOLUTIONS TO THE SYSTEM OF OPERATOR EQUATIONS AXB=C=BXA∗
- BURKHOLDER-GUNDY-DAVIS INEQUALITY IN MARTINGALE HARDY SPACES WITH VARIABLE EXPONENT∗
- CHAIN CONDITIONS FOR C∗-ALGEBRAS COMING FROM HILBERT C∗-MODULES∗
- SINGULAR LIMIT SOLUTIONS FOR 2-DIMENSIONAL ELLIPTIC SYSTEM WITH SUB-QUADRTATIC CONVECTION TERM∗
- THE REPRESENTATION OF THE SOLUTION OF STURM-LIOUVILLE EQUATION WITH DISCONTINUITY CONDITIONS∗
