基于特征能量函数的故障暂态量时频特征分析

胡加伟， 应 鸿， 邹 晖， 姜 涛， 张亚刚

(1.华北电力大学 电气与电子工程学院，河北 保定 071003； 2.浙江华云清洁能源有限公司，浙江 杭州 310008； 3. 国网浙江省电力有限公司 检修分公司，浙江 杭州 310008)

0 引言

随着我国电力系统向长距离、大容量、特高压、智能化、全国互联的方向发展，形成了以特高压为主干网，交直流混联的电网格局，这难免就对系统的安全稳定运行提出了更高的要求，而系统要具有高稳定裕度的前提是当线路发生各种类型故障的时候，继电保护装置能够快速的动作，将线路故障对系统带来的冲击影响降到最低。基于故障暂态分量的线路保护较当前的基于工频信号的保护原理具有不受系统震荡、过渡电阻和故障初始相角等因素的影响[1,2]，而且随着对线路故障机理的深入认识，信号采集和传输通道等相关技术的革新，以及小波分析及与小波分析相结合的分析算法的出现，使得基于暂态量的线路保护能够实现区内故障快速准确动作不拒动，区外故障可靠不误动[3,4]。由于基于故障暂态分量的线路保护较基于工频分量展现出来的一系列优势，新型的基于故障暂态分量的线路保护逐渐成为电力系统继电保护的重点研究方向。

暂态保护的思想是通过提取和放大线路发生各种类型故障后的暂态过程中产生的高频宽带信号来实现的线路保护。故障暂态量信号中包含了大量贯穿整个时间频域的关于线路故障类型、故障距离、故障持续时间等信息，通过合适的数学分析方法将这些故障信息提取出来，可以实现故障的类型判别、故障测距、故障选相、自适应重合闸等一系列功能[5,6]。由于超高压交流输电线路故障时会产生宽带高频的暂态电流，这些高频暂态电流成分在经过线路边界时能量会大幅度地衰减,进而造成高频成分能量的损失，故会形成天然的区内、外的故障判据[7]。

故障暂态电流信号由于频率高、幅值小，时域上的波形特征并不是特别明显。故单纯的提取信号的时域特征或者单纯的提取信号的频域特征是不够的，因为故障时产生的暂态电流信号具有奇异性和非平稳性，信号频率是时间的函数[8]。本文选择有“信号显微镜”之称的小波变换理论，利用其优良的局部化时频分析的特点[13]，并采用Db4正交基小波来对故障暂态信号进行故障信息提取，分析信号的局部化时频特征[9,10]。

1 暂态量来源及小波分析

1.1 故障高频暂态量来源

由故障分析理论可知：超高压交流输电线路发生各种类型的区内、外故障时，会产生从工频到上百千赫兹高频的暂态量。高频暂态分量主要由频率及能量都相对集中的部分和具有较宽频带、能量分布较均衡的部分组成[11,12]。线路故障时暂态信号的主要来源有以下3大方面：

(1)行波的透反射。线路故障时暂态行波在故障点和线路边界间的来回透、反射会产生一系列宽带高频的暂态分量。

(2)电弧的熄灭与重燃。线路故障后断路器中电弧的反复熄灭与重燃会产生一系列高频宽带的暂态分量。

(3)行波的色散现象。线路故障过程中不同频率的暂态行波在线路上的传播速度与衰减程度不同，也会产出一系列的宽带高频暂态分量。

输电线路故障时宽带高频的故障暂态分量来源多样，且其中包含了贯穿整个时频域的有关故障相别，故障类型及故障距离等故障信息，充分挖掘故障暂态电流中隐藏的这些故障信息，可实现故障测距、选相、自动重合闸等功能。

1.2 离散小波变换

目前，小波理论在电力系统继电保护领域的应用已相当广泛且成熟，如故障识别、故障选相、自适应重合闸等方面[13,14]，本文主要利用了小波变换的多分辨率及局部化时频分析的特点。

如果φ(t)∈L2(R)满足允许性条件：

(1)

则称φ(t)为基小波，其中Φω是φ(t)经过傅里叶变换在频域的形式。在基小波的基础上，通过改变尺度因子a和时间因子b值的大小生成的小波函数系可表示为：

(2)

式中：a,b∈R,a>0,a和b分别与频率和时间相关。将信号在这个函数系上做分解，就得到L2(R)的信号f(t)的连续小波变换(CWT)定义：

(3)

如果小波φ(t)∈L2(R)满足完全重构条件，信号f(t)可由其连续小波变换系数Wf(a,b)重构得到，变换公式如下：

φa,bWf(a,b)dadb

(4)

综上，还可以同时得到在不同尺度因子a和位移因子b下的小波变换时间窗和频率窗的定义，具体可表示为：

(5)

随着尺度因子a的变化，窗口函数的时间窗、频率窗也会跟着改变。即a增大，则时间窗变宽而频率窗变窄。可以通过选取不同的尺度因子a来调节时间窗和频率窗的比例，同时改变位移因子b来获取到信号在任何时间、任意感兴趣的频谱，由此可以看出小波变换较傅里叶变换的优势，不仅可以将时域及频域联系起来，更能实现对信号的局部化时频特征分析。

因为现在信号采样得到的数据都是离散的，而且为了提高小波变换的效率，消除不必要的变换冗余，故提出离散小波变换(DWT)，即将尺度参数a,b同时离散化，一般取对应的离散小波φj,k为：

j,k∈Z

(6)

则经过离散小波变换得到的小波系数可表示为：

(7)

将式(6)和式(7)代入式(4)可得到由离散小波变换的小波系数还原信号的重构公式为：

φj,k(t)

(8)

式中：C为常数，其大小与基小波及分解算法有关，而与分析信号无关，如果基小波是正交的，则离散小波变化即可去除冗余。则此时可表示为:

f(t)=fN(t)=

fN-M(t)+gN-M(t)+…+gN-1(t)=

(9)

在一定的精度下，gj(t)代表信号f(t)的高频细节系数，包含着信号f(t)的细节信息，对它进行相关处理，可实现信号降噪，图形复原等功能；fN-M代表信号f(t)的低频近似系数，它是信号的逼近，可以通过它来预测信号未来的趋势与状态。

2 基于小波能量的暂态量时频特征分析

由于小波变换具有敏感的变焦特性和多尺度检测的能力，可以实现对全频域各个频带信号的特征信息提取。本文基于离散小波变换，用位于窗函数固定窗内的离散小波变换系数的平方和来得到不同分解层数下对应的小波能量[14,15]。随着窗函数扫过全时间域，便可得到不同频带对应的小波能量谱，并在此基础上选择两个特定的频带，构造出特征能量函数。设小波变换在尺度2j1和2j2上的能量为Ej1和Ej2：

(10)

(11)

式中：ΔT为时间步长；K为比例系数；M为窗口采样数；KRatio为特征能量函数比值；WIm为固定窗内小波变换系数。若取j2>j1，即Ej1为高频部分，Ej2为低频部分。当输电线路发生故障时，Ej1和Ej2均会有显著突变，以此可作为保护的启动判据。由前面的分析，因为线路两端加有阻波器和母线对地电容等构成的线路边界的存在，区外故障的时候，高频暂态电流分量经过线路边界时，会有很大程度的衰减。即区内故障时，保护安装处电流互感器TA检测到的故障暂态电流中高频暂态电流的能量要远远大于区外故障时的，故区内故障时KRatio会比区外故障时大。调整合适的比例系数，可通过KRatio的大小来判别区内、外故障。为增强抗干扰能力，可用KRatio大于定值持续时间是否超过设定的时间阈值来判定区内故障。

3 算例仿真验证及分析

3.1 算例仿真验证

利用PSCAD/EMTDC仿真软件搭建了如图1所示超高压交流输电仿真系统。线路模型采用Bergeron模型，线路参数分别为：正序阻抗Z1= 0.015 4+j0.278 2 Ω/km，零序阻抗Z0=0.046 1+j0.833 6 Ω/km，线路对地正序电容为C1=0.013 0 μF/km，对地零序电容为C0=0.004 4 μF/km。母线对地电容CP=0.1 μF。

线路两端还装有线路阻波器，这里选用的型号为：XZF-3150-2.0/63-B1，详细参数如下：L1=2 mH、C1=528 pF、L2=0.338 mH、C2=3 125 pF、R=800 Ω，工作频率为48～500 kHz。线路MN长300 km,线路NP长100 km。故障点分别设置在区内距保护安装处105 km和区外正向出口10 km处。

图1 500 kV双端输电系统

这里采样频率为200 kHz，以Db4小波为基小波来对进行模量变换后的故障电流信号进行离散小波变换，得到模量Im在第一、二层分解上的离散小波变换系数D1(50～100 kHz)及D2(25～50 kHz)。窗函数的窗宽参数设置为M=500，即MΔT=2.5 ms，比例系数K整定为10。仿真时长为[0,0.15 s],在PSCAD/EMTDC仿真系统中设置在t=0.1 s时刻发生区内、外单相金属性接地故障。

3.2 数据分析

当高压交流输电线路发生各种类型的故障时，由于输电线三相之间甚至双回线路之间会存在互感耦合现象。为消除这种现象，电力系统继电保护领域中广泛应用了模变换技术，为了更加适应故障类型的任意性，本文选择模变换为Im=Ia+Ic-2Ib来对电流互感器TA测得的三相电流值进行解耦处理[16]。

对比图2和图3可得：三相故障电流信号经过模量变换后的波形，区内故障的模分量波形畸变要比区外发生故障时严重得多，说明在区内故障时，保护安装处电流互感器TA检测到的故障电流中，将包含更多的高频暂态分量；而发生区外故障时，绝大部分的高频暂态电流将会在经过线路边界时发生透、反射而衰减掉，故波形的畸变程度不大。且线路发生区内、外故障时，模量的波形差异并不是特别明显，故单纯的从时域上去判别区内还是区外故障是不现实的；而且，线路故障时产生的是宽带高频故障暂态电流，与基频稳态短路电流相比，无论是在幅值上、还是在频率上差距均较大，故单纯的从频率上进行分析也是行不通。所以要利用离散小波变换对信号进行局部化的时频特征分析。

图2 区内故障时故障电流

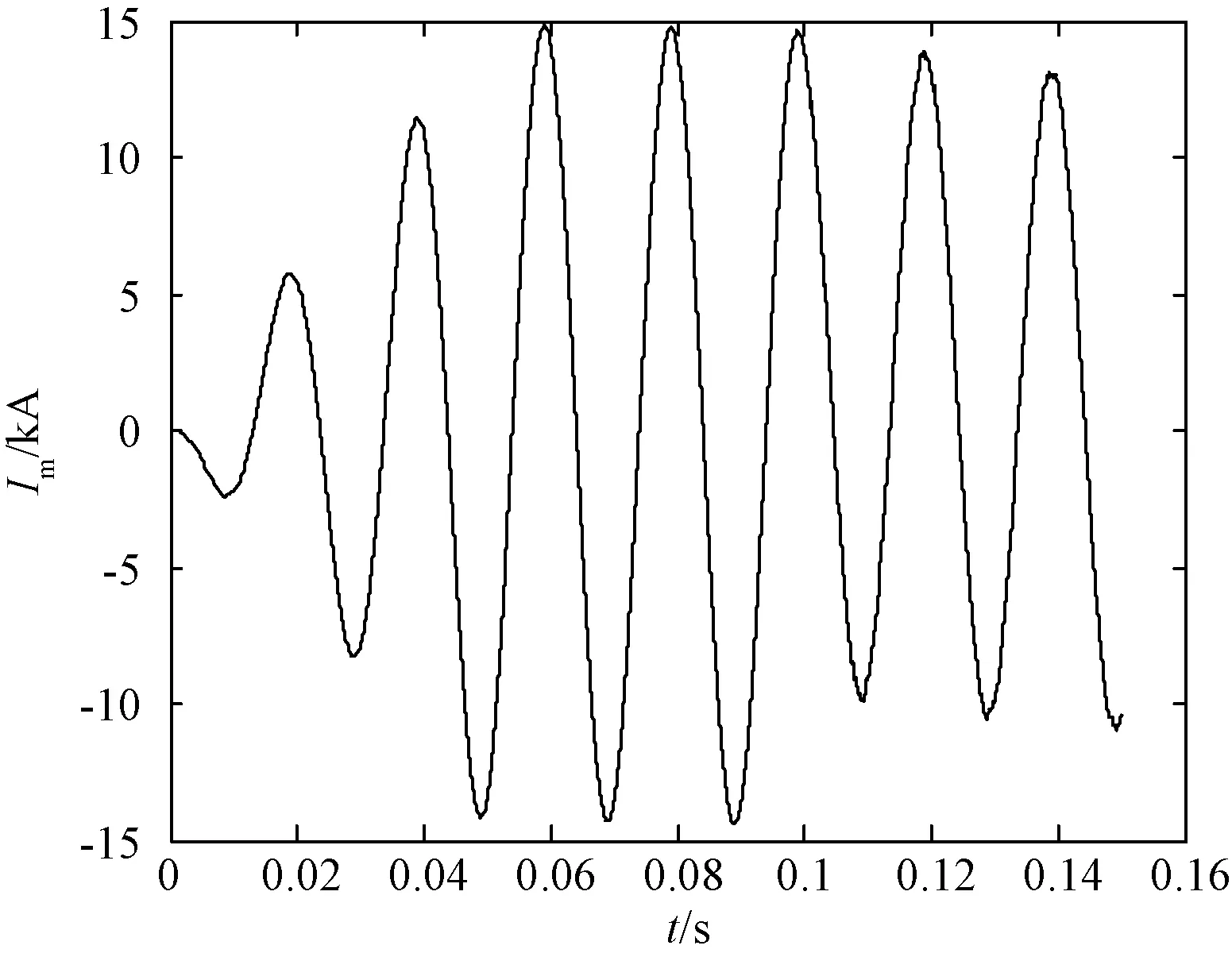
图3 区外故障时故障电流

进一步可得D1细节系数的小波能量谱，对比图4和图5可知，在t=0.1 s时发生故障，这时发生区内、外故障，能量谱均会发生突变，由此可作为保护启动的依据。

图4 区内故障D1的能量谱

图5 区外故障D1的能量谱

然后再利用特征能量函数比值KRatio的大小来区分究竟是发生了区内故障，还是发生了区外故障。根据以上的理论分析可知，当发生区外故障时，由于母线对地电容和线路高频阻波器组成的线路边界的存在，区外高频故障电流分量在经过线路边界时会大量的衰减，故高频部分的能量值大小较区内故障要大很多，故区内故障时的特征能量函数比值KRatio会远大于区外故障时的特征能量函数比值KRatio。如图6和图7所示，区外故障时KRatio<1,区内故障时KRatio>2，该判据可作为区分区内、外故障的判别依据。

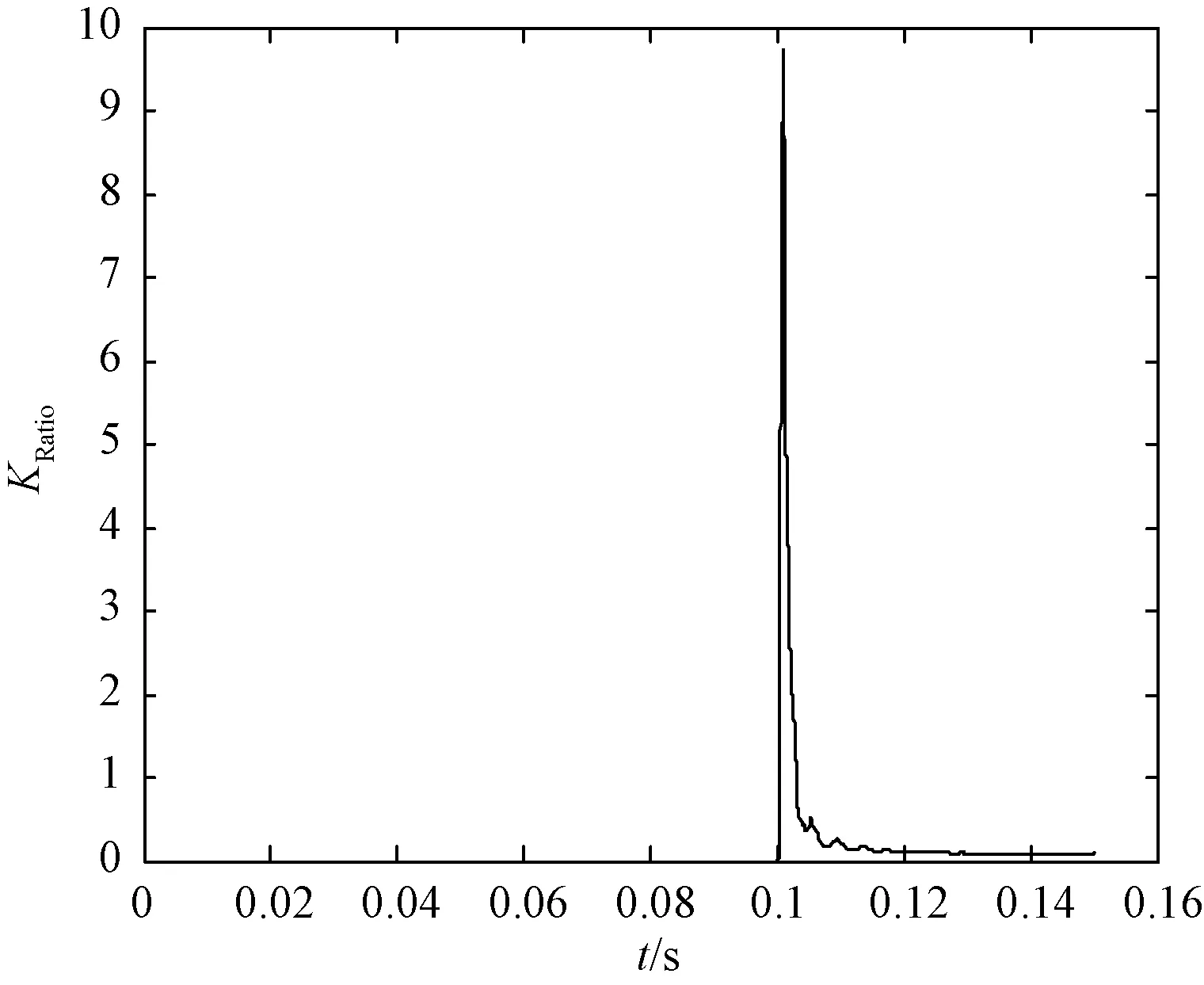
图6 区内故障时KRatio

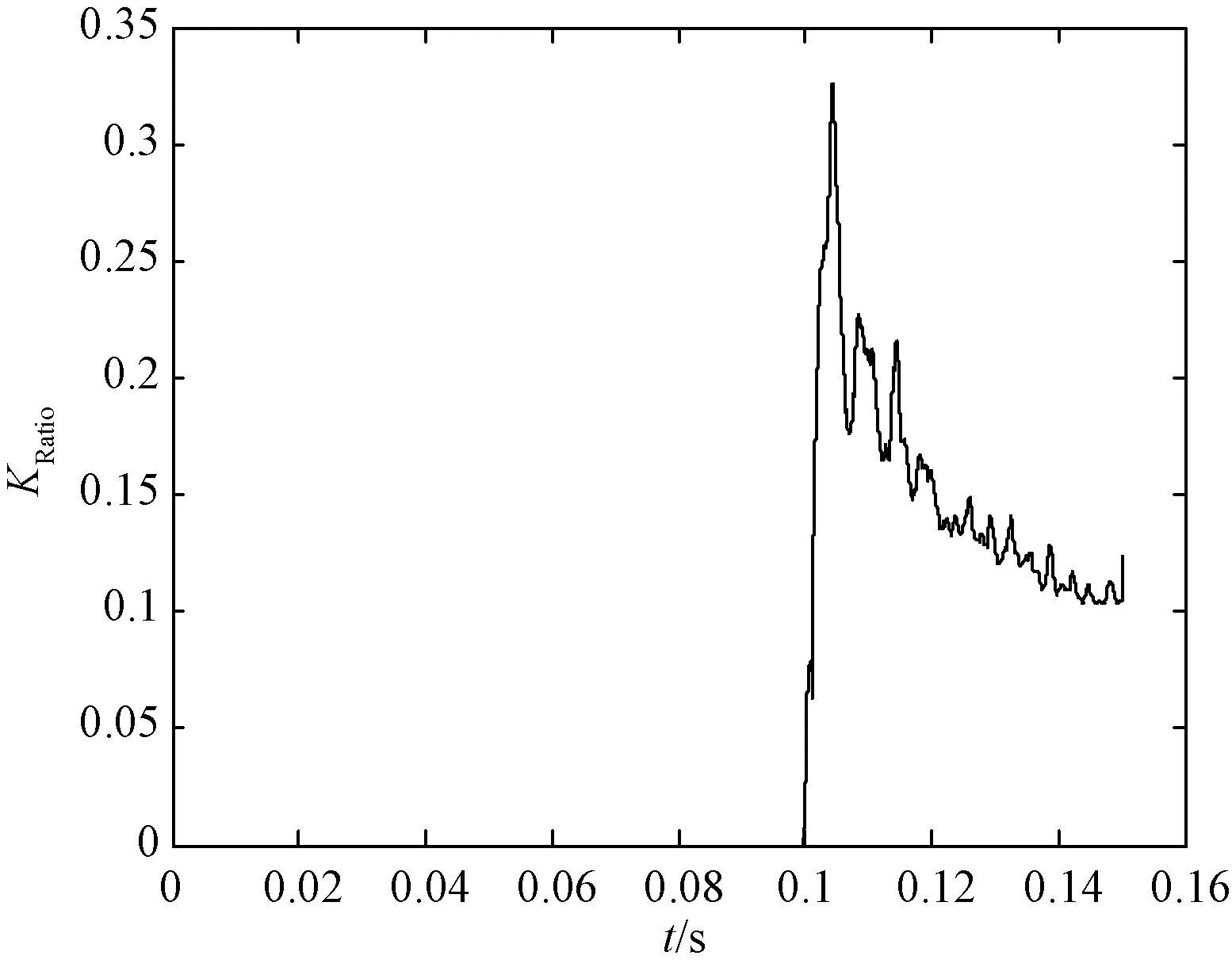
图7 区外故障时KRatio

当判别出区内故障的时候，需要对故障进行定位，由图8可知，区内故障时的特征能量函数的突变点要迟于PSCAD/EMTDC仿真系统设定故障时间(t=0.1 s)，这相当于暂态电流分量从故障点传播到TA端的时间，根据电力系统暂态过程分析理论可知：线路故障产生的暂态量将会在故障点和线路边界(TA安装处)之间来回的透反射，故可以根据这个原理来实现故障测距。

由于故障时刻未知，本文利用暂态电流两次到达TA的时间差，来实现故障测距，此后的波头由于暂态电流行波在来回透、反射的过程中发生了混叠而无法进行故障的测距。具体算法为：通过寻找D1细节系数的前两个模极大值之间的时间差，然后确定电流在线路上的传播速度，便可以通过速度与时间计算得到故障点到保护安装处的距离，实现故障测距。如图9可知，通过理论计算可得故障点L=106.5 km,误差为1.4%。

图8 区内故障时KRatio

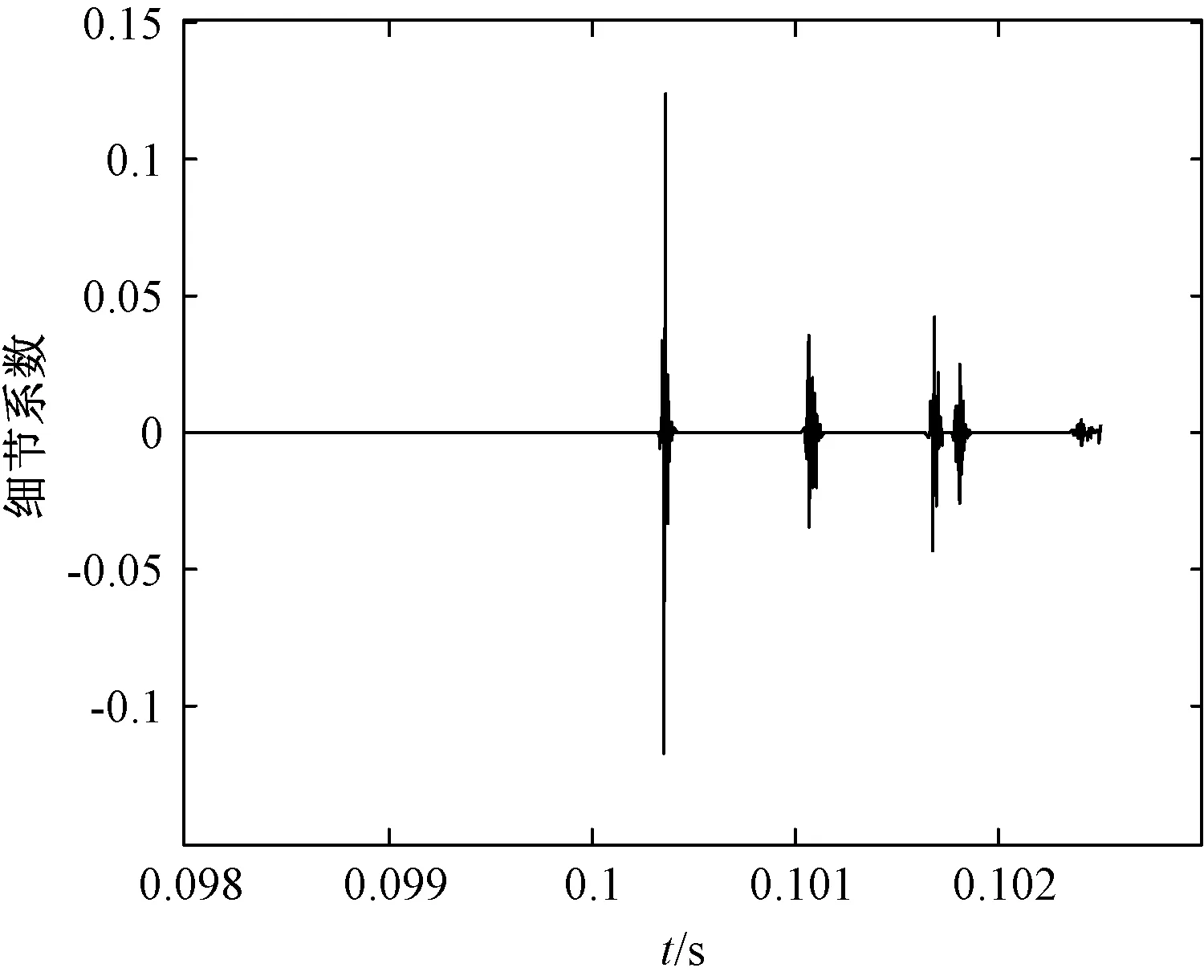
图9 D1细节系数

4 结论

本文基于对超高压交流输电线路故障时的暂态过程及故障后区内、外暂态量分布特征的深入研究，提出了利用小波能量谱来构造“特征能量函数”，进而对输电线路发生区内、外故障时产生的暂态量进行时频特征分析。通过该算法对数据进行时频特征提取可得：当线路发生区内、外故障时，细节系数D1的小波能量谱均会发生突变，可作为保护启动的判据；而当区内故障时KRatio>2,区外故障时KRatio<1，由此可作为保护动作的判别依据。经过大量仿真结果表明，该算法受故障类型、过渡电阻、故障初始相角等因素影响小，具有较好的适应性；整个暂态时频分析过程仿真计算方便、快捷，区内外故障特征明显，可为基于线路故障暂态分量保护提供新的保护判据，实现区内故障快速准确动作，区外故障可靠不误动，同时实现故障测距。