一种架空输电线路电气可靠度的评估分析方法

唐 巍， 李育兵， 黎 亮， 许 泳， 梁 明， 王理智

(西南电力设计院有限公司，四川 成都 610021)

0 引言

架空输电线路的可靠性是指输电线路能够安全、稳定运行的程度。输电线路可靠性评估是指根据线路的特性和多年来运行信息，运用统计学概率估计理论和方法，计算线路发生故障的可能性，即线路可靠度。

目前国内学者对电力系统、输电线路杆塔结构子系统的可靠性进行了大量的研究[1～5]，但对输电线路电气可靠性能评估尚缺乏系统性的研究，而输电线路往往爬山涉水、周围环境及气象等条件比较复杂，易发生因污秽、雷击、覆冰等引起的闪络跳闸故障。为了确保电网的安全运行,加强输电线路电气可靠性方面的研究,保障输电线路安全可靠运行已经迫在眉睫。

通过科学、先进的评估方法，充分利用各种信息对线路可靠度进行分析，首先，可以检验线路设备是否达到了可靠性要求，并验证可靠性设计的合理性；其次，可以预测线路各类电气事故的总故障率及故障易发地段，发现线路的薄弱环节，为工程建设及运行采取相应的防范措施提出建议[5]；再次，在当前在线监测、故障诊断等技术尚不完善，在线监测设备普遍比较昂贵的情况下，通过可靠性评估获知线路安全程度，也是一种行之有效的手段[6～9]。

1 架空输电线路闪络模型

架空输电线路各种情况下的闪络模型是建立线路电气可靠度模型的基础。针对引起输电线路闪络的原因，可将其分为污秽闪络、覆冰闪络和雷击闪络3种类型。

污秽闪络模型基于线路沿线污秽分布、盐密等级、绝缘子串型式等情况，将整条线路划分为不同的区段，利用污闪概率模型计算线路污秽闪络的发生概率。覆冰闪络模型依据线路沿线覆冰厚度及相应的覆冰天数，将整条线路划分为不同的区段，利用冰闪概率模型计算线路覆冰闪络的发生概率。雷击闪络模型利用电气几何模型(EGM)计算绕击闪络率，同时利用ATP模型计算线路的反击概率，结合绕击和反击模型计算线路雷电闪络概率。

2 线路电气可靠性评估理论基础

2.1 可靠性理论基础概述

可靠度是指元件在规定的条件下和规定的时间内完成规定功能的概率，与可靠度相对应的是不可靠度，它表示产品在规定的条件下和规定的时间内，不能完成规定功能的概率。可靠度与不可靠度呈互补关系。计算公式如下：

R+Q=1

(1)

式中：R为可靠度；Q为不可靠度。

输电线路是由导线、绝缘子、杆塔等元件通过串联[3]、并联或串并联[1，2]组成的系统。系统可靠性不仅与组成系统各单元的可靠性有关，而且也与组成该系统各单元间的组合方式和相互匹配有关。系统及其单元之间的可靠性逻辑关系和数量关系是通过系统可靠性模型来反映的，它是系统可靠性预测和分配的前提。

工程系统可靠性分析中，常利用网络图形的形式模拟元件或子系统的可靠性能以及相互间的影响。根据系统原理图、元件与系统的功能关系，按系统可靠性等效的原则绘制的网络图形，称之为可靠性框图。可靠性框图由代表元件的方框、逻辑关系连接和节点组成。实际工程系统一般由元件串联、并联、网状或者这三者组合的模式联结构成。

2.2 复杂系统的割集法

实际电力系统的结构往往不是简单的串联、并联或串并联关系，如图1所示的桥型网络结构，对于这类网络的分析往往非常复杂[4]，通常采用条件概率法、割集法、或连集分析法、树图法等进行可靠性分析。

图1 桥型网络

割集法中导致系统失效的元件集合的最小子集称为最小割集，只要最小割集中任何一元件没有失效，就不会造成整个系统失效。基于系统最小割集进行可靠性分析的方法即为最小割集法[6～8]。

在系统可靠性逻辑框图中，由于同一元件出现在多个最小割集中，故不能直接应用串联系统的概率计算公式，而需要应用“并”集的原理进行计算。计算公式如下：

Qs=P(C1∪C2∪C3…∪Ci∪…∪Cn)

(2)

式中：Qs为系统不可靠度；Ci为第i个最小割集；P(Ci)为第i个最小割集发生概率。

2.3 干涉模型法原理

若元件故障是由于外界的某种因素超过了该元件对该因素所能承受的绝缘强度，就可以采用干涉模型来描述。通常将该因素称为荷载，干涉模型也可称为荷载—强度分布干涉模型。由于荷载和强度都是随机变量，因此荷载、强度两概率密度函数曲线在一定条件下可能发生相交，其相交的区域称为干涉区域，即元件可能出现故障的区域。输电线路的荷载包括作用在绝缘子上的过电压、污秽和覆冰等，则元件的可靠度可表示为：

Pr=P(R-Q>0)

(3)

式中：Pr为元件的可靠度；Q为作用在绝缘上的荷载包括加过电压、污秽、覆冰等；R为原件的绝缘强度。

假设式(3)中R和Q的概率密度函数分别为fr(r)与fq(q)，累积概率密度函数分别为Fr(r)与Fq(q)，则失效概率与可靠度可用强度与荷载之差的概率密度函数积分求得。

设两个随机变量之差Z的联合概率密度函数为fz(z)，Z的概率密度函数可表示为：

(4)

Z<0时的概率既是失效概率可表示为：

(5)

3 污闪电压及污闪概率计算

在一定盐密值下的污闪电压通常具有一定的分散性，但一般认为其服从正态分布[10]，因此需要得到50%污闪电压及变差系数，50%污闪电压的大小通常与盐密值、绝缘子型号、绝缘子串长等有关。

3.1 盐密或灰密对污闪电压的影响

通过人工或自然污秽试验的目的是求得不同污秽度下绝缘子的耐受电压或闪络电压。完整的污秽试验先用一系列基础污秽度的试品，进行闪络和耐受试验，求得对应的耐受电压或闪络电压，对试验数据采用回归法分析，得到绝缘子污耐受或污闪电压随污秽度变化的规律。大量试验结果及其分析表明，污秽绝缘子的闪络电压与污秽程度有关，也就是说，既与等值附盐密度有关，也与不溶于水的惰性物质的密度即灰密有关，试验结果表明，盐密和灰密对污闪电压影响的规律是一致的[11～12]，均可以表示为：

Uf=K·X-p=A(SDD)-a=A·S-a

(6)

Uf=K·X-p=B(NSDD)-b=B·G-b

(7)

式中：Uf为绝缘子耐受或污闪电压；X为绝缘子的污秽度；K为系数，可通过人工污秽试验求得；a为污秽中盐密对污闪电压影响的特征指数；b为污秽中灰密对污闪电压影响的特征指数。

3.2 线路污秽闪络概率计算

绝缘子表面积污情况受运行时间、污秽环境、自然界雨水冲刷等众多因素的影响，但从长期来看绝缘子污秽程度通常不存在积累效应，而是一个随机概率值。绝缘子的污闪电压服从正态分布[10]，当绝缘子串的污闪电压及其标偏系数选定后，一串绝缘子在一次雾湿天气下发生污闪的概率可按下式计算：

(8)

式中：U线路运行电压；Uj(p)为绝缘子串的50%污闪电压；σj(p)为Uj(p)的标准偏差。

绝缘子的盐密值通常服从对数正态分布可按下式计算：

(9)

式中：ρ为盐密值；u为ρ的对数的平均值；为ρ的对数的标准差。

综上所述，在一次湿雾天气下绝缘子污秽闪络的概率[11]可采用下式计算：

(10)

若假设单串绝缘子闪络一次便发生一次故障，则I串绝缘子为串联系统。因此可计算一次湿雾天气下湿雾天气范围内线路的污闪概率：

PI=1-(1-P′(p))I

(11)

4 冰闪电压的影响因素及冰闪概率计算

在一定覆冰厚度下的冰闪电压通常具有一定的分散性，但一般认为其服从正态分布，因此需要得到50%冰闪电压及变差系数，50%冰闪电压的大小通常与覆冰厚度、绝缘子型号、绝缘子长度、盐密值有关。

4.1 绝缘子覆冰冰闪电压计算

国内外相关试验成果均表明，覆冰绝缘子冰闪电压与监测导体覆冰厚度、覆冰前染污程度、绝缘子型式以及覆冰水电导率均有关[13～17]。在实际运行线路所处的自然环境下，覆冰水电导率变化一般并不明显，绝缘子型式也是确定的，但覆冰厚度和覆冰前的污秽程度则是随机参量，因此，对于具体的输电线路，要确定的是覆冰前污秽程度和覆冰厚度综合作用下直流输电线路绝缘子串的冰闪特性。综合冰闪电压与覆冰厚度、覆冰前染污以及与串长的关系，可得绝缘子(串)的50%直流冰闪电压的一般关系按下式表示：

U50=Ad×d-md×S-a=

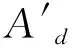
(12)

4.2 线路覆冰闪络概率计算

由于绝缘子覆冰情况，运行电压作用下线路塔头部分闪络引起跳闸的主要原因是覆冰绝缘子串闪络，故本文在计算时只考虑绝缘子在覆冰天气的闪络情况。

在一定覆冰厚度及盐密值下，绝缘子串的冰闪电压服从正态分布，当线路绝缘子串的冰闪电压及其标偏系数选定后，一串绝缘子在一次雾湿天气下发生冰闪的概率可按下式计算：

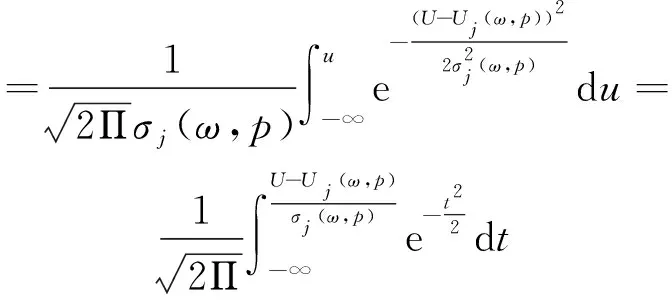
(13)

式中：U为线路运行电压；Uj(ω,p)为绝缘子串的50%冰闪电压；σj(ω,p)为Uj(ω,p)的标准偏差。

每年覆冰厚度按照覆冰最大值计算，年覆冰极值满足极值I型分布，设计重现期假设为T年，则有在T年间线路覆冰超过设计值的概率为1/T，其概率密度函数可按下式计算：

g(ω)=aexp{-a(ω-u)-exp[-a(ω-u)]}

(14)

式中：a为尺寸参数；u为位置参数；ω为覆冰厚度；σ为标准差。

因此在一次覆冰天气中绝缘子闪络的概率按照下式计算：

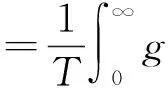
(15)

若假设单串绝缘子闪络一次便发生一次故障，则N串绝缘子为串联系统。因此可计算一次覆冰天气下线路的冰闪概率：

PN=1-(1-P′(ω))N

(16)

5 雷击闪络概率计算

根据文献[18～21]采用EGM击距法计算绕击闪络率，采用EMTP-ATP模型计算反击闪络率。

输电线路沿线采用塔型繁多，设在同一地形下各塔型的绕击闪络率为λi，考虑不同塔型的交叉使用，则线路的平均绕击闪络率可计算为：

(17)

式中：N为总塔型数目；ωi第i种塔型在全线所占的百分比。

考虑地形的多变性，即山区、丘陵与平地3种地形，则线路的绕击闪络率可计算为：

(18)

式中：η山地、λ丘陵、λ平地代表山地、丘陵与平地在全线所占的百分比。

若每年的雷暴天数为M，则可求出线路的不可靠度为：

(19)

6 算例

以糯扎渡送电广东±800 kV直流输电线路工程为例，应用前文中的方法计算其电气可靠度。糯扎渡送电广东线路工程途经云南、广西、广东共计3个省区，线路全长约1 438 km。线路经过地区大部分为山区，伴有丘陵、平地，其中高山大岭约409.6 km，占28.5%；一般山地约695.8 km，占48.4%；丘陵约266.1 km，占18.5%；平地约66.5 km，占4.6%。线路最高海拔2 200 m。导线采用6×LGJ-630/45钢芯铝绞线，地线采用LBGJ-180-20AC铝包钢绞线。设计基准风速取27 m/s、28 m/s、30 m/s、33 m/s四类风区。设计覆冰有0 mm、10 mm、15 mm三类冰区。

6.1 污闪可靠性计算

6.1.1 绝缘子污闪概率计算

由于湿雾天气影响范围并不大，因此考虑湿雾天仅对100 km以内的直流输电线路有影响。一年中湿雾天数为40天时各分组绝缘子串的闪络的概率如表1。

表1 污闪概率表

6.1.2 污闪可靠性灵敏度分析

(1)湿雾天数对线路污闪可靠度的影响

当年湿雾天数从10～70天变化时，线路可靠度的变化曲线如图2所示。

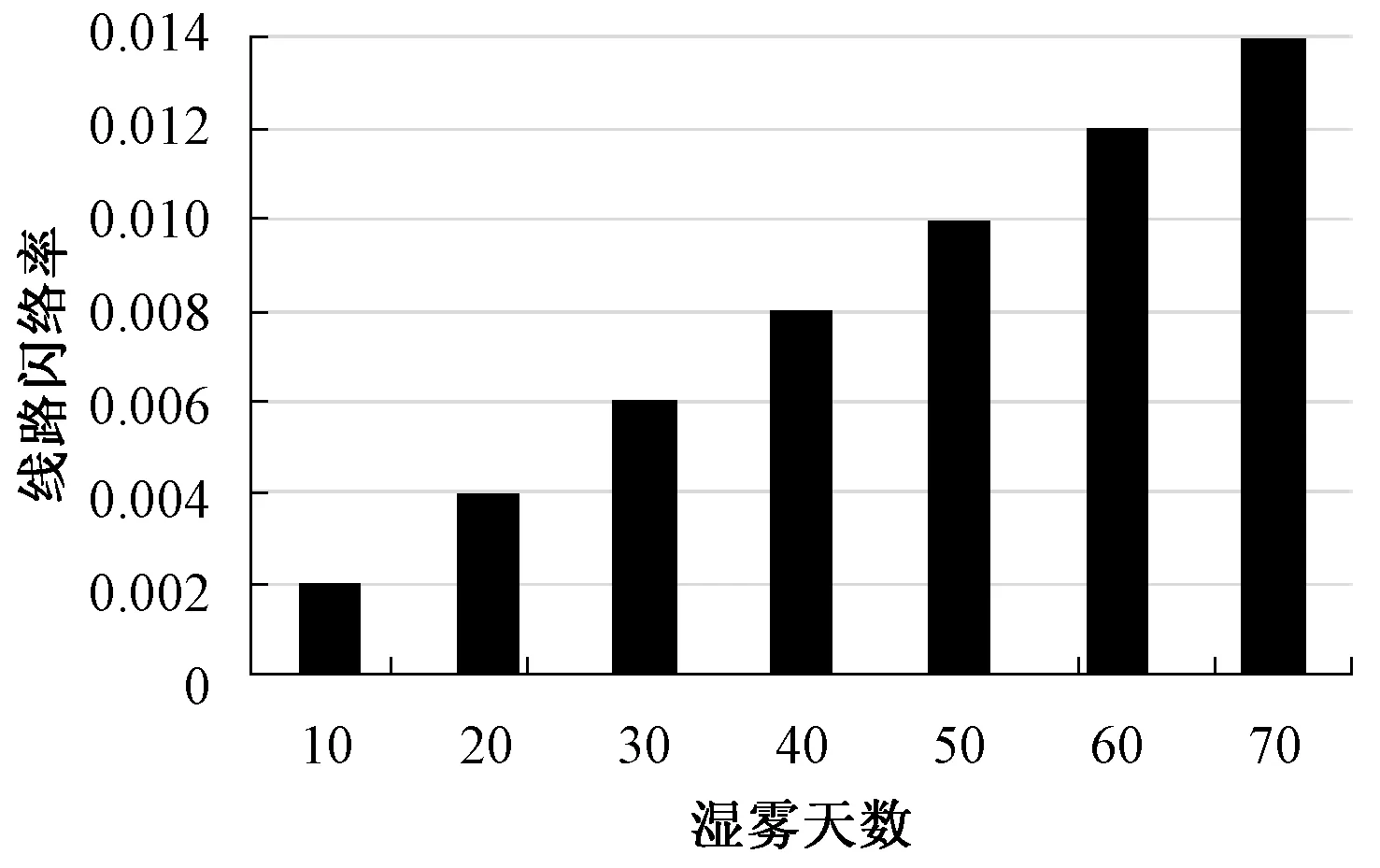
图2 湿雾天数对线路闪络率影响曲线

从图2可以看出，当湿雾天数从10～70天变化时，线路闪络率由0.002次/100 km·a上升到0.014次/100 km·a，说明年湿雾天数对线路的闪络率有一定的影响，但是影响不大，线路可靠性始终保持在一个较高的水准。

(2)湿雾天气影响范围对线路污闪可靠度的影响

当湿雾天气影响范围从100 km增大到400 km时，线路的不可靠度如图3所示。

图3 湿雾天气影响范围对线路可靠度影响曲线

随着湿雾天气影响范围的增大，线路可靠度逐渐降低，当湿雾天气影响范围增大到400 km时，线路可靠度降低到99.92%。线路可靠性始终保持在一个较高的水平，故障率较低。

6.2 冰闪可靠性计算

6.2.1 绝缘子污闪概率计算

各污区内等值盐密按照设计盐密常遇值取值，各冰区覆冰厚度服从极值I型分布，再考虑中冰区覆冰的情况。一年中覆冰天数取为15天时各分组绝缘子串的冰闪概率如表2。

表2 冰闪概率表

6.2.2 冰闪可靠性灵敏度分析

当年覆冰天数从0～30天变化时，线路闪络率的变化曲线如图4所示。

图4 覆冰天数对线路闪络率影响曲线

从图中可以看出，当覆冰天数从0～30天变化时，线路的闪络率由0次/100 km·a升高到了0.0016次/100 km·a，说明年覆冰的天数对线路的闪络率有一定的影响，但线路可靠性水平很高，影响不大。

6.3 雷击闪络可靠性计算

6.3.1 雷击闪络概率计算

全线在不同地形下的平均绕击闪络率、平均反击闪络率如表3。

表3平均绕击/反击闪络率(次/100 km.a)

角度平均绕击闪络率平均反击闪络率(双回)0°00.003 110°00.009 620°0.079 10.018 2

注：按全线平均雷暴日80天计算。

6.3.2 雷击闪络可靠性灵敏度分析

当年雷暴天数从0～80天变化时，线路可靠度的变化曲线如图5所示，线路不可靠度的变化曲线如图6所示。

图5 雷暴天数对线路可靠度影响曲线

从图5、图6中可以看出，当雷暴天数从0～80天变化时，线路的可靠率由1降低到了0.986 2，而线路不可靠度则由0升高到了0.013 8，说明年雷暴的天数对线路的可靠度有一定的影响。

综上，应用本文的可靠性评估方法计算得出糯扎渡送电广东线路工程在污秽、覆冰、雷击情况下的可靠性指标，表明线路工程可靠度位于一个较高的水平，线路能够稳定运行，计算数据与实际运行情况吻合。

7 结论

对架空输电线路进行可靠度分析评估，对提高输电线路安全运行能力具有重要意义。本文应用荷载—强度分布干涉模型，采用最小割集可靠性评估理论，结合输电线路污秽、覆冰、雷击3种闪络模型，提出了架空输电线路电气可靠度综合评估分析方法。通过算例糯扎渡送电广东±800 kV直流输电线路可靠度的分析计算可以看出，特高压直流线路的可靠度水平位于一个较高的水平，湿雾天数及其影响范围、覆冰天数、雷暴天数对输电线路电气可靠度存在一定影响，但不会影响输电线路的稳定运行。