导弹轨控喷流气动干扰全空域插值方法研究

李欣益，刘 伟，唐海敏，傅建明

(上海机电工程研究所，上海 201109)

0 引言

近年来，弹道导弹、超声速巡航导弹等高速目标的威胁日益增大。这类目标速度极快，一般都以超声速甚至高超声速在大气层中运动，导致防空导弹的拦截时间缩短，留给导弹末制导修正脱靶量的时间也被大大压缩，这对导弹的机动性、灵敏性提出了更高要求。传统空气舵控制的导弹对过载指令的响应速度为几百毫秒量级，滞后效应较严重，面对高速目标时，导弹响应速度需达到数十毫秒的量级，单纯采用空气舵控制的导弹难以有效减小脱靶量。而直接力控制的导弹对过载指令的响应速度可达10 ms量级，可满足防空导弹拦截高速目标的需求。

侧向喷流与来流相撞产生复杂的干扰流场。当喷流从飞行器表面喷出时，喷流本身会产生反作用力，和外流发生强烈碰撞后，会引起激波-边界层干扰、边界层分离、旋涡等复杂的流动现象，改变飞行器局部表面的压力分布，产生附加的力和力矩[1]，即产生气动干扰。

与常规气动力不同，侧向喷流气动干扰会随海拔高度(以下简称高度)的不同而发生显著变化。因此，为满足全空域使用轨控喷流的要求，必须提供不同高度下的喷流气动干扰数据。然而，受经费及研制周期的限制，往往只能对有限的高度进行喷流气动干扰计算，这就要求我们必须研究侧向喷流气动干扰随高度变化而发生变化的机理，从中发现规律，从而寻找到一种有效、可靠的插值方法，实现有限数据下不同空域的喷流气动干扰数据插值。

目前，国内外已针对侧向力直-气复合干扰做了大量研究工作[2-6]。中国空气动力学研究与发展中心、中国航天空气动力技术研究院等研究机构也进行了很多前沿性的探索[7-11]。文献[1]开展了一系列风洞试验，分析了侧向喷流干扰的流动机理和喷流参数的影响规律。文献[9-10]对侧向喷流计算的湍流模型、差分格式、网格生成方法进行了深入研究。然而，这些研究多侧重于对流动机理、流动现象的阐述和对数值计算方法的探索，较少涉及不同空域下喷流气动干扰对导弹气动特性的影响和相应的插值方法。

传统的全空域喷流气动干扰插值都是基于高度插值来进行的，该方法较为直观，然而在空气动力学的控制方程和边界条件中，高度的变化实际只体现在雷诺数和侧向喷流与来流的压力比的变化上。雷诺数会影响导弹边界层厚度，压力比会影响喷流马赫盘形状，从而导致侧向喷流气动干扰发生变化。因此，基于高度的插值方法在气动原理上缺乏理论依据。

本文通过数值计算，着重研究了不同空域下雷诺数和压力比对轨控喷流气动干扰的影响，提出了一种基于压力比的插值方法。与基于高度和雷诺数的插值方法相比，该方法精度更高，所需数据量更少，可为全空域喷流气动干扰建模提供依据。

1 相似准则及数值方法

本文主要通过数值方法来分析不同空域下不同参数对轨控喷流气动干扰的影响。工程上导弹采用的侧向喷流均为燃气喷流，因国内目前主要采用冷喷模拟热喷的方法来进行相应的风洞试验和数值模拟[1]，故首先必须明确冷热喷转换的相似准则，并验证数值方法计算结果的准确性。

1.1 相似准则

参考GJB4012-2000，按照动量相似、压力比相似、出口面积相似等原则确定喷管参数和喷流参数为

(1)

1.2 计算模型及数值方法

计算外形为尖拱-柱-舵的旋成体模型，选取“×”型布局进行计算。因侧向喷流流场中包含复杂的波系和涡系结构，且存在流动的分离与再附等复杂的流动现象，故选择三维可压缩雷诺平均N-S(Navier-Stokes)方程为控制方程[12-15]。通过有限体积方法进行离散，湍流模型采用一方程S-A(Spalart-Allmaras)模型。采用整体结构化网格，对壁面和喷口附近的网格进行加密处理。对近壁面网格开展网格无关性研究，最终选取的近壁面网格高度为0.05 mm，网格单元总量为1.4×107。网格拓扑及喷口处网格如图1、2所示。

图1 导弹空间网格视图Fig.1 Grid distribution of missile

图2 喷口网格视图Fig.2 Grid distribution of lateral jet

1.3 数值计算与风洞试验对比

为验证数值计算方法的准确性，将CFD (computational fluid dynamics)计算结果与某风洞试验结果进行对比，法向力和俯仰力矩系数的对比曲线如图3、4所示。图中：马赫数Ma=2.0，雷诺数Re=3 447 583，压力比pj/p∞=14.87。

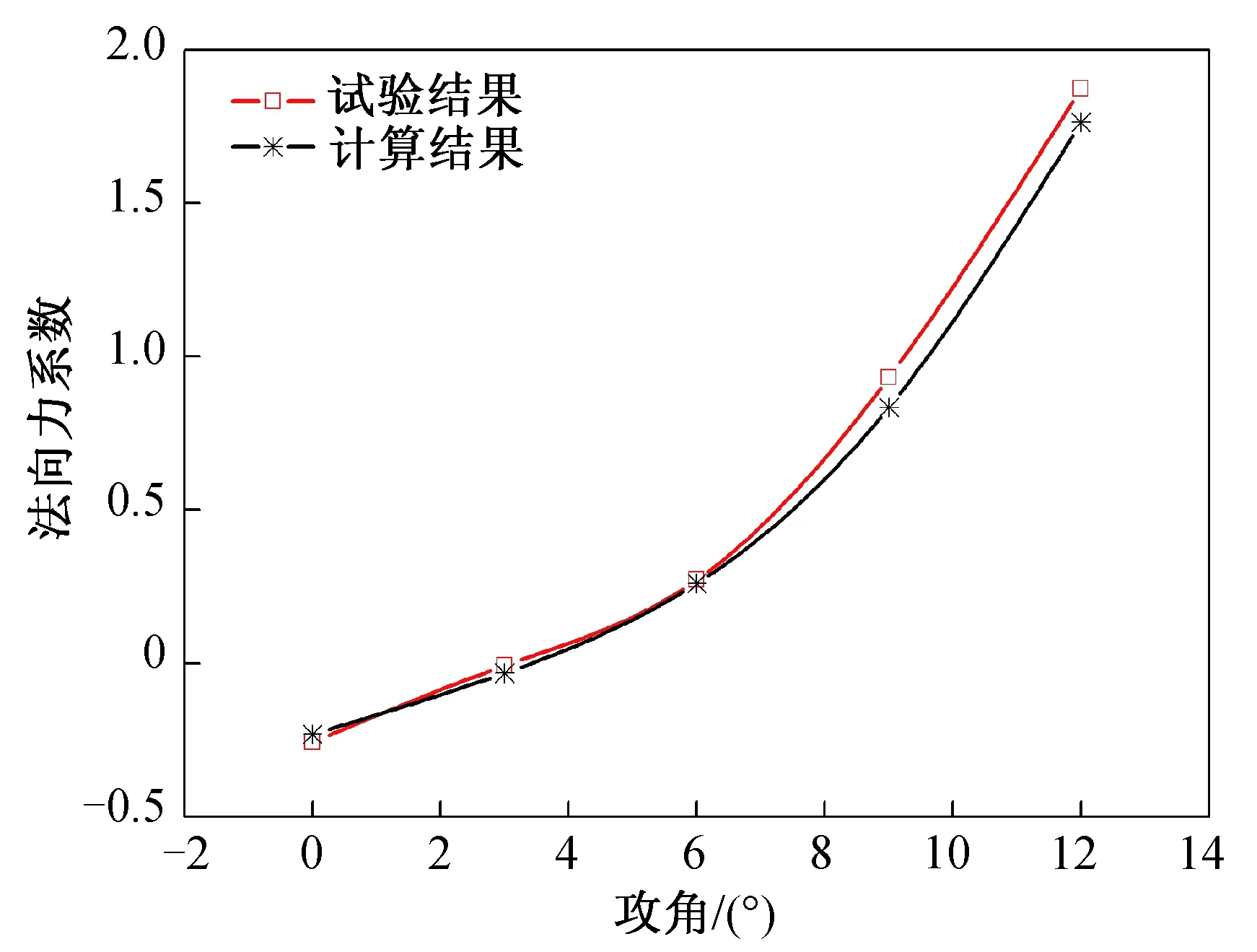
图3 法向力系数CFD计算与试验对比Fig.3 Comparison of normal force coefficients by CFD calculation and experiment

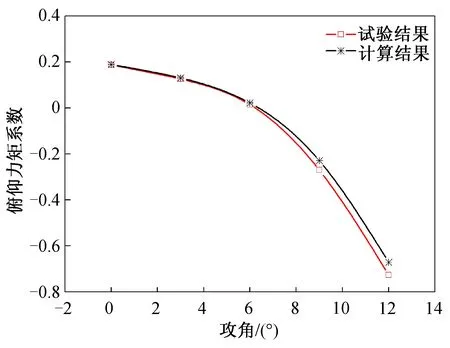
图4 俯仰力矩系数CFD计算与试验对比Fig.4 Comparison of pitching moment coefficients by CFD calculation and experiment

由图3、4可以看出，本文采用的数值模拟方法结果可靠，可用于侧向喷流干扰流场的特性分析。

2 雷诺数影响分析

雷诺数随高度的变化而变化，导致边界层厚度发生变化，从而对喷流气动干扰产生影响。为分析雷诺数对喷流气动干扰的影响程度，统一取8 km处的压力比计算不同高度的喷流气动干扰，相关计算参数见表1。

雷诺数的表达式为

Re=ρvl/μ

(2)

式中：Re为雷诺数；ρ为大气密度；v为导弹速度；l为导弹长度；μ为大气黏性系数。ρ，μ随高度变化而变化，从而影响雷诺数。

六分量的喷流干扰气动系数表示为

ΔCi=ΔCi_jet-ΔCi_nojet

(3)

式中：ΔCi_jet，ΔCi_nojet分别为气动系数六分量的有喷值(不包含喷流推力/力矩系数)、无喷值。计算结果见表2。

表1 计算参数

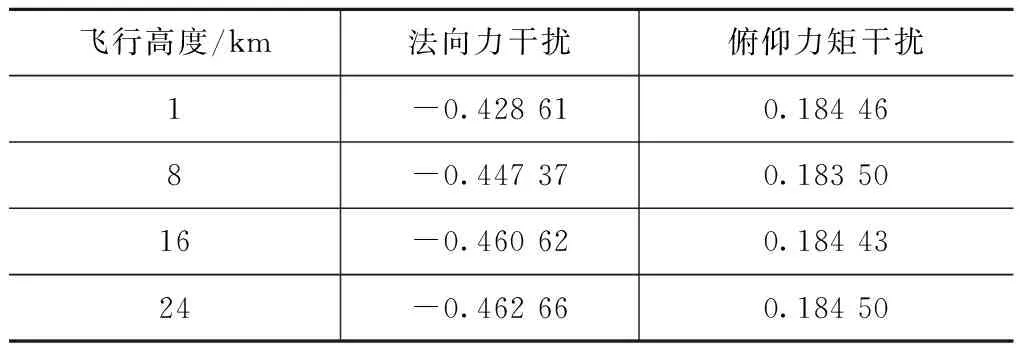
表2 计算结果

从表2可以看出，由于雷诺数不同，相比于8 km处的计算结果，不同高度的法向力干扰最大相差3%，俯仰力矩干扰最大相差1%。对于表1中1 km和8 km两种高度下的计算状态，图5、6分别给出了导弹上下表面中间线上的压强系数对比。可以看出，就轨控喷流而言，雷诺数的变化对气动干扰量影响较小。

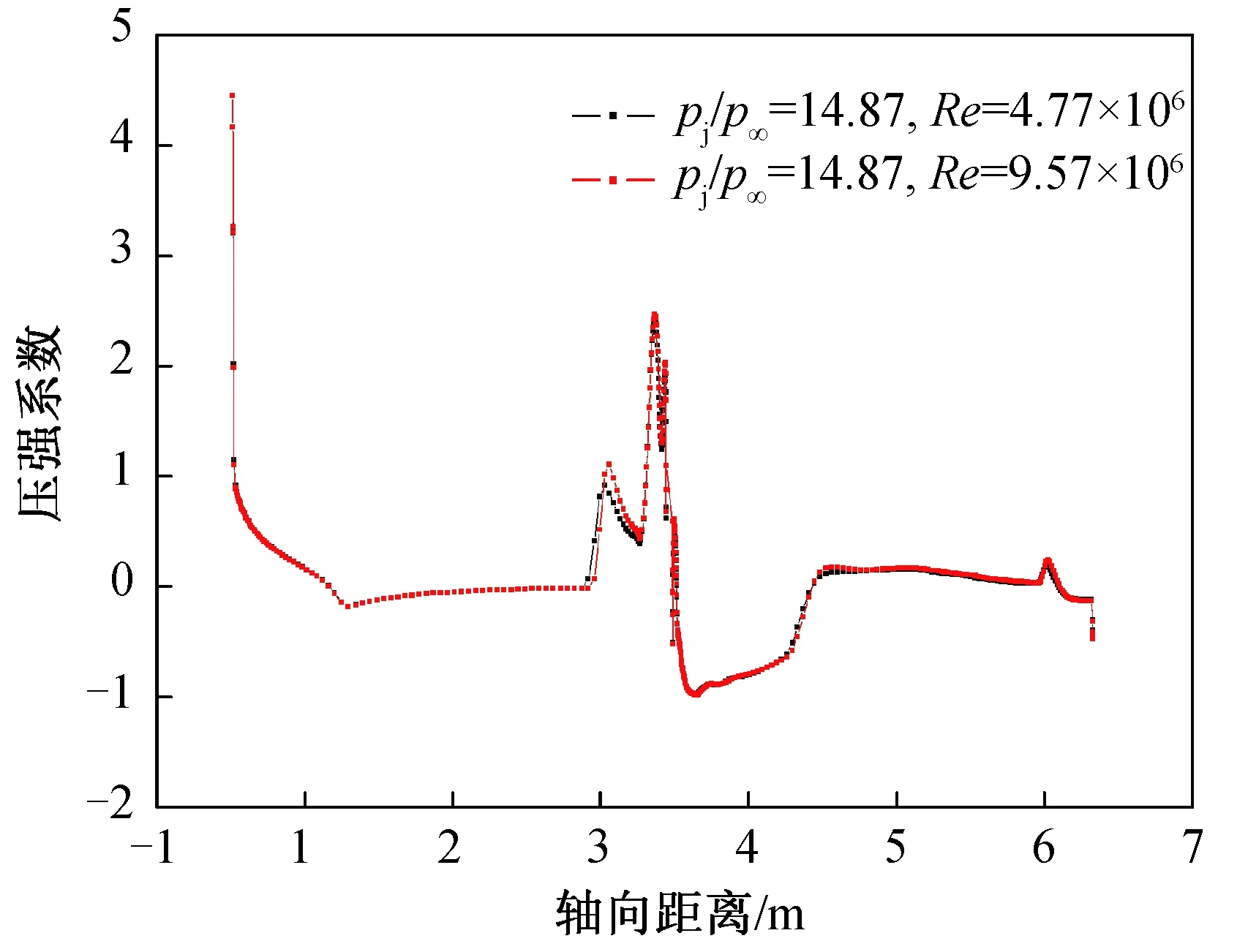
图5 不同雷诺数下对称子午线压强系数分布(下表面)Fig.5 Pressure coefficient distribution on symmetric meridian for different Reynolds numbers (lower surface)

图6 不同雷诺数下对称子午线压强系数分布(上表面)Fig.6 Pressure coefficient distribution on symmetric meridian for different Reynolds numbers (upper surface)

3 压力比影响分析

除雷诺数外，压力比也会随高度的变化而变化。此处，压力比为喷管出口静压与来流静压的比值。作为喷流模拟的重要相似参数，压力比的变化将造成波系结构、压力分布发生改变。

统一取8 km处的雷诺数，对不同压力比下的喷流干扰进行计算，相关计算参数见表3，计算结果见表4。

表3 计算参数

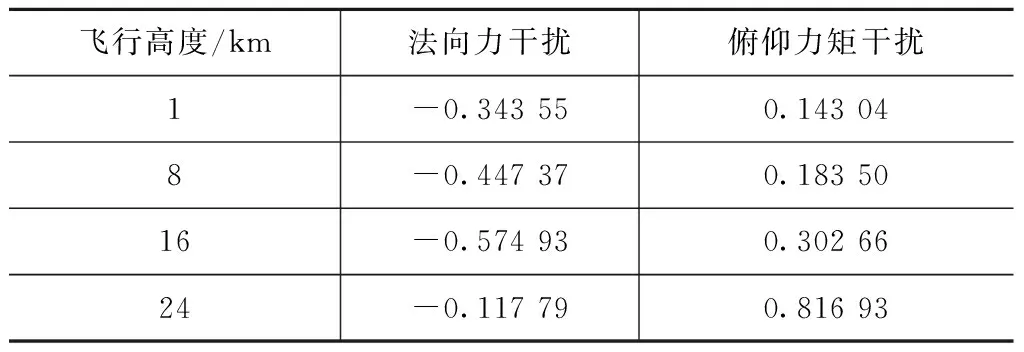
表4 计算结果

由表4可知，在不同高度，由于压力比发生变化，法向力干扰和俯仰力矩干扰变化显著。对于表3中1 km和8 km两种高度下的计算状态，图7、8分别给出了导弹上下表面中间线上的压强系数对比。可以看出，压力比变化带来的影响远大于雷诺数变化带来的影响。

图7 不同压力比下对称子午线压强系数分布(下表面)Fig.7 Pressure coefficient distribution on symmetric meridian for different pressure ratios (lower surface)

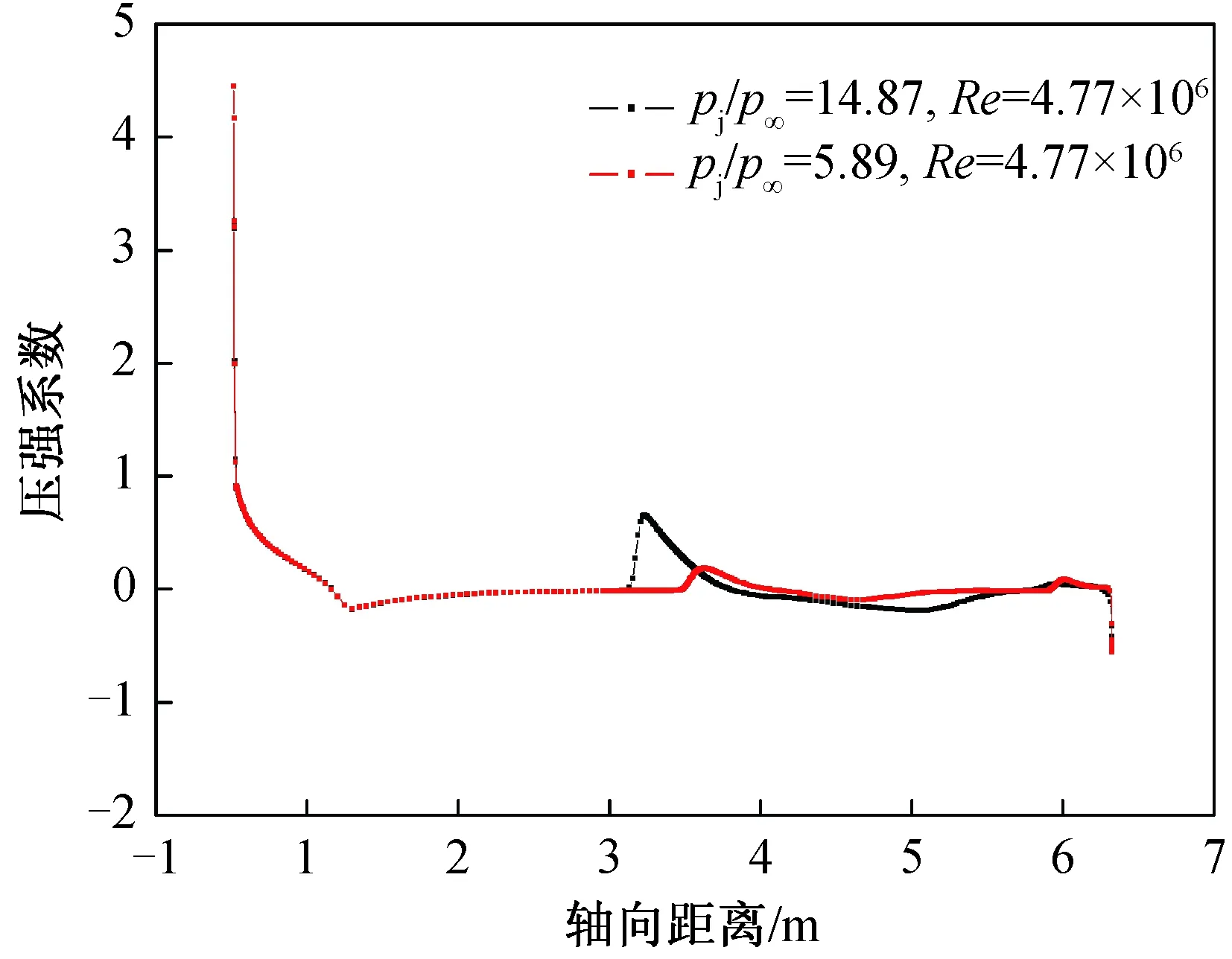
图8 不同压力比下对称子午线压强系数分布(上表面)Fig.8 Pressure coefficient distribution on symmetric meridian for different pressure ratios (upper surface)

4 不同海拔高度下喷流气动干扰插值

为满足不同高度条件下使用轨控的要求，需研究不同空域下喷流干扰的插值方法。对于该问题，传统方法是基于高度进行插值，但从前面章节的分析中可以看出，就轨控喷流而言，高度对喷流气动干扰的影响实际由雷诺数和压力比的变化造成，其中又以压力比变化带来的影响为主。喷流气动干扰的大小与高度值并无直接关系，传统的基于高度的插值方法在气动原理上缺乏理论依据。因此，本文认为应对基于雷诺数或压力比的插值方法进行研究。

为比较基于高度、雷诺数、压力比的3种插值方法的优劣，对表5中的状态进行了计算，并分别给出了喷流气动干扰随高度、雷诺数和压力比变化的曲线，如图9～14所示。

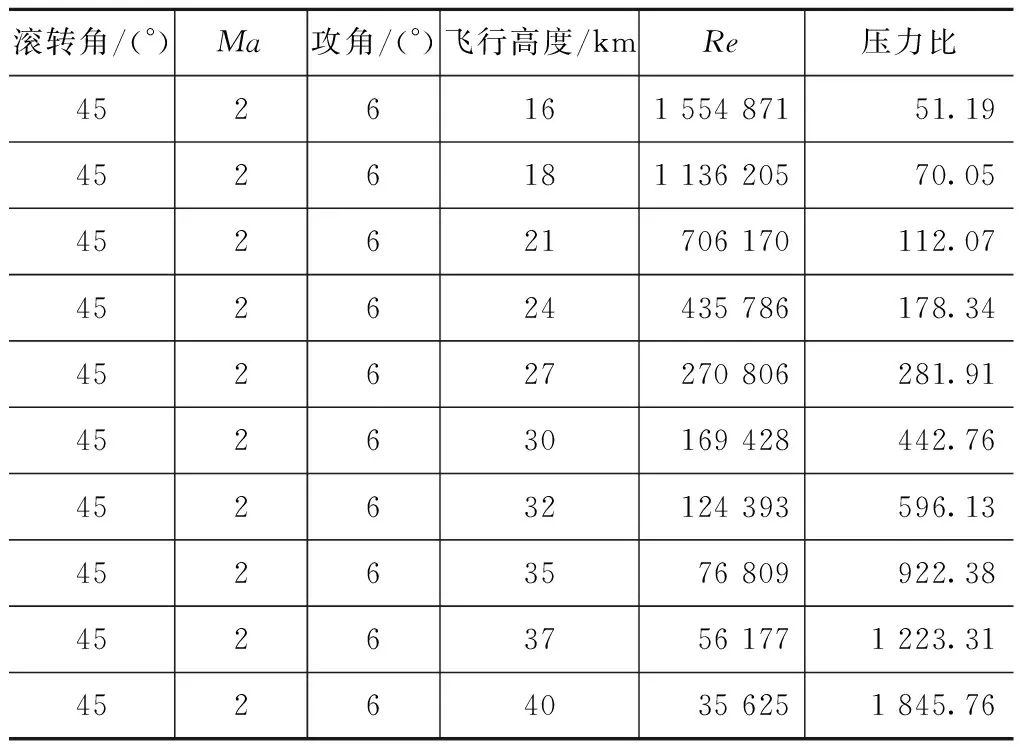
表5 计算参数

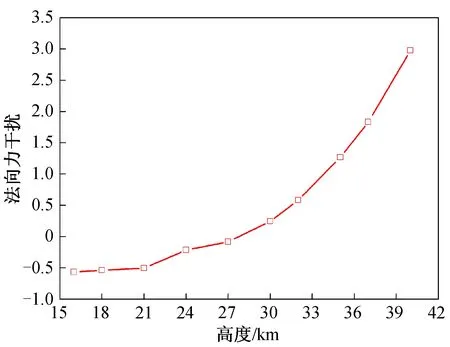
图9 法向力干扰随高度变化曲线Fig.9 Variation of normal force interaction with altitude

图10 俯仰力矩干扰随高度变化曲线Fig.10 Variation of pitching moment interaction with altitude

图11 法向力干扰随雷诺数变化曲线Fig.11 Variation of normal force interaction with Reynolds number

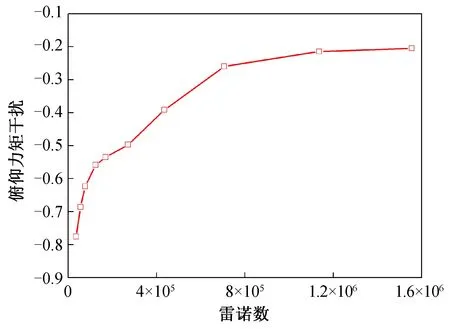
图12 俯仰力矩干扰随雷诺数变化曲线Fig.12 Variation of pitching moment interaction with Reynolds number

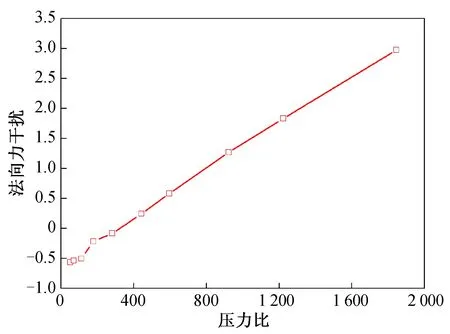
图13 法向力干扰随压力比变化曲线Fig.13 Variation of normal force interaction with pressure ratio

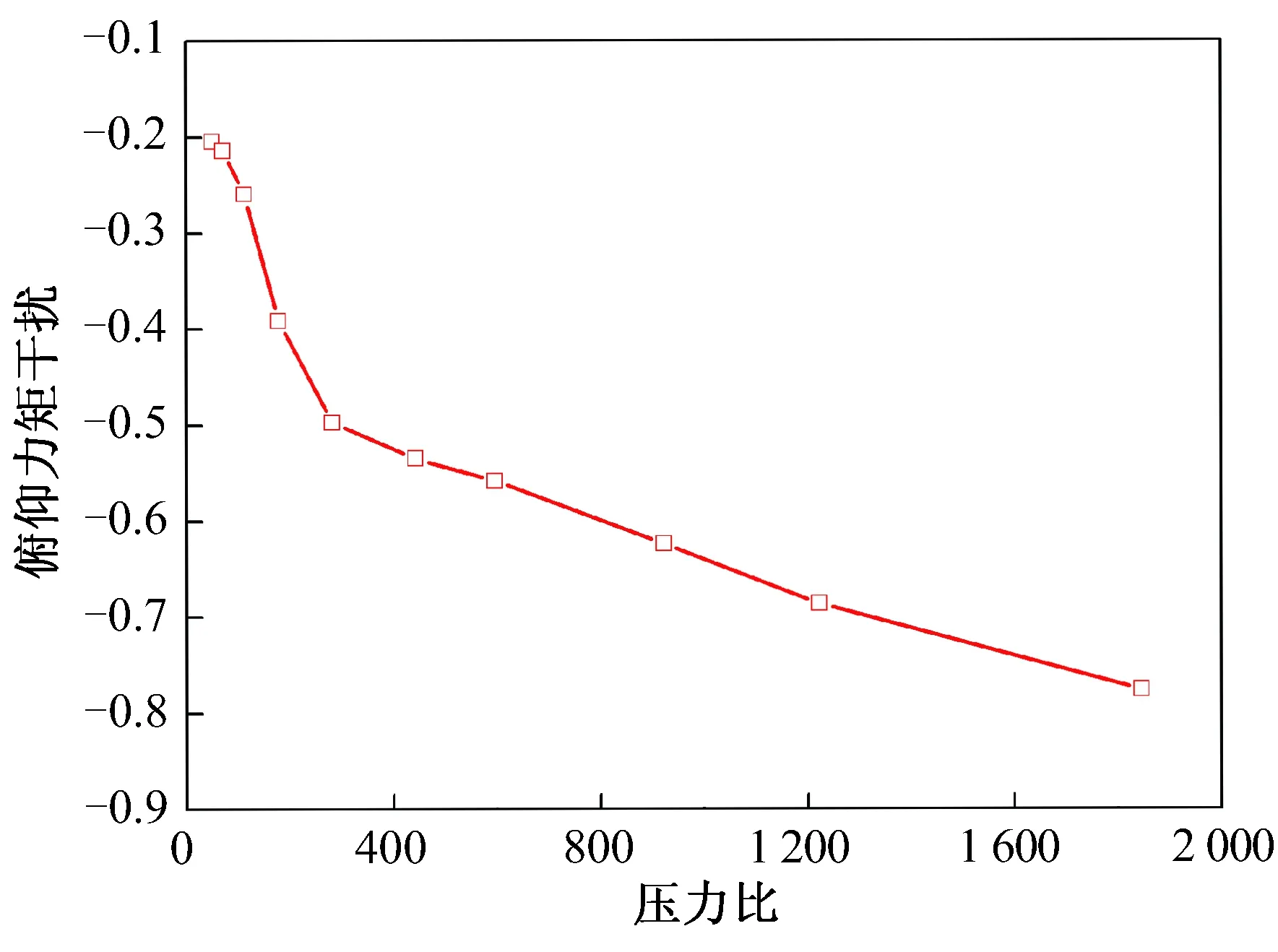
图14 俯仰力矩干扰随压力比变化曲线Fig.14 Variation of pitching moment interaction with pressure ratio

从图9～ 14可以看出，由喷流产生的法向力和俯仰力矩干扰随高度、雷诺数和压力比的变化均呈非线性变化，直接采用两点间线性插值会带来较大误差，必须划分出线性度较好的区间，采用分段线性插值来提高精度。其中：喷流干扰随压力比变化曲线的线性度最好，随高度变化曲线的线性度其次，随雷诺数变化曲线的线性度最差；喷流气动干扰在不同的区间随压力比呈现一定的线性关系。因此，可考虑采用基于压力比的分段线性插值来提高插值精度。

在进行分段线性插值的过程中，既要保证插值精度，又要尽量减少插值节点以减少计算量和成本。综合分析图9、10、13、14可以看出，在16～40 km范围内，21，27 km是喷流干扰的2个较为明显的拐点。因此，为在保证插值精度的同时减少计算量，如只能选取4个插值点，则可取16，21，27，40 km这4个高度作为插值节点，分别按高度和压力比线性插值，结果如图15～18所示。

图15 法向力干扰按高度线性插值Fig.15 Linear interpolation of normal force interaction with altitude

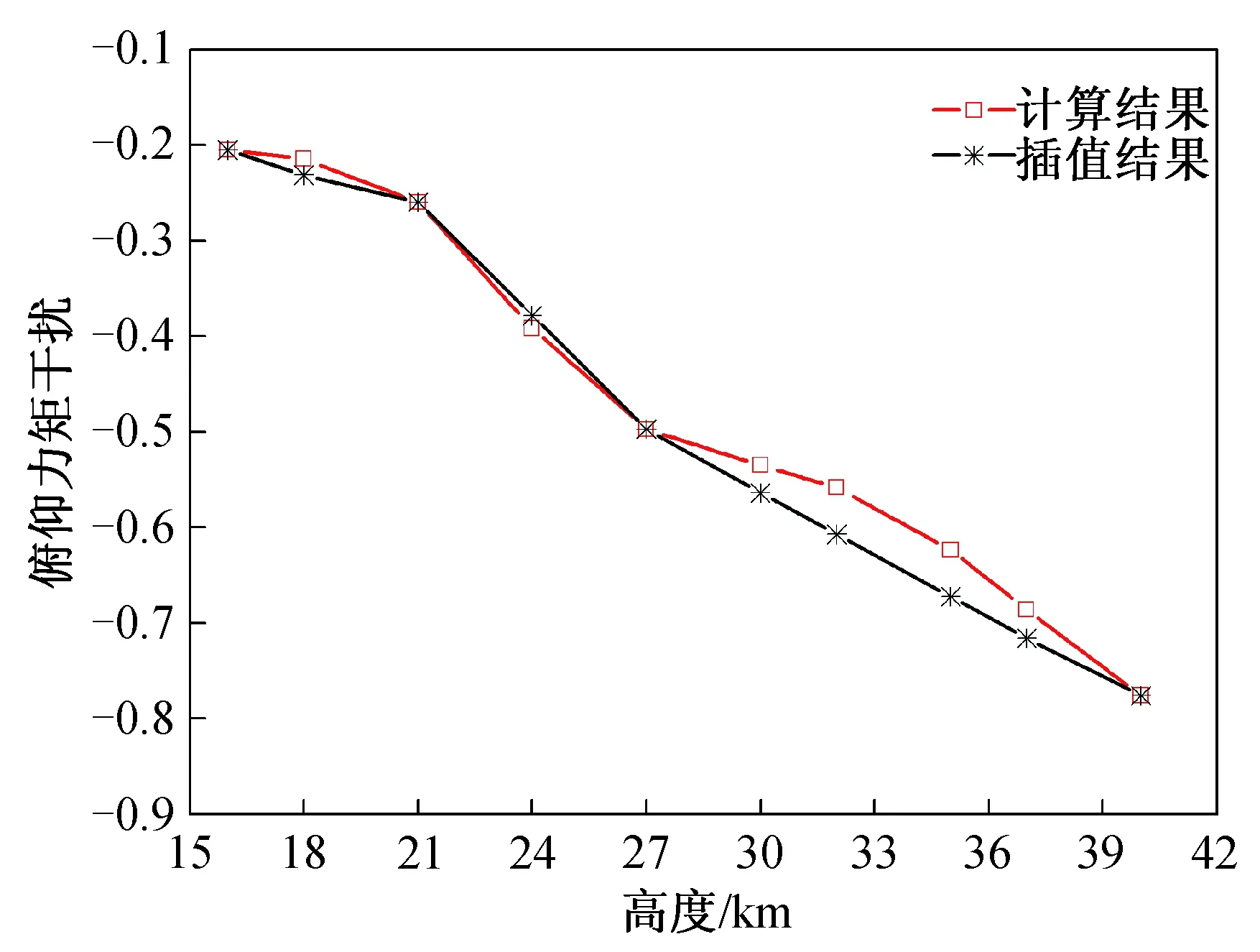
图16 俯仰力矩干扰按高度线性插值Fig.16 Linear interpolation of pitching moment interaction with altitude

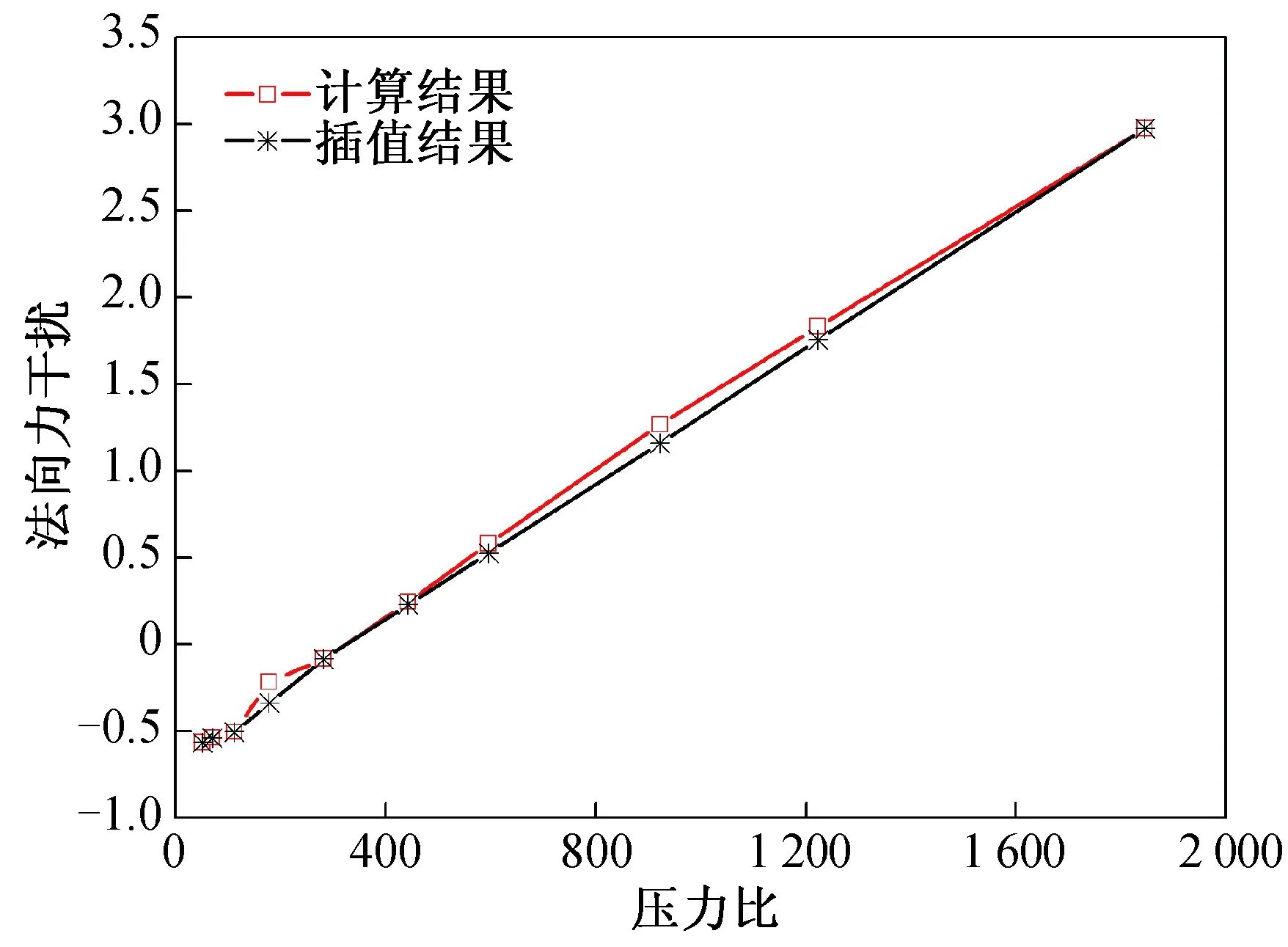
图17 法向力干扰按压力比线性插值Fig.17 Linear interpolation of normal force interaction with pressure ratio

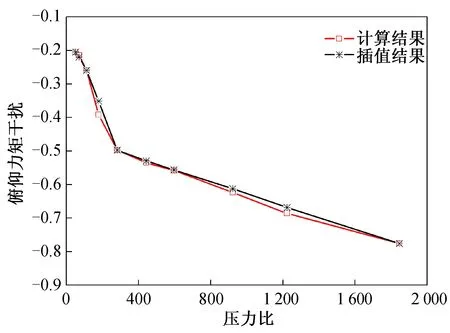
图18 俯仰力矩干扰按压力比线性插值Fig.18 Linear interpolation of pitching moment interaction with pressure ratio

从图15～18可以看出，在27 km以下，2种插值方法获得的结果均与计算值较为吻合，误差较小，而在27 km以上，按压力比线性插值的误差要明显小于按高度线性插值。在保证精度的条件下，如果要按高度线性插值，则必须在27～40 km范围内增加插值节点，这就导致计算量和成本大大增加。因此，与按高度线性插值相比，按压力比线性插值精度更高，同时能减少插值节点数。

5 结论

分析表明，在小攻角轨控喷流状态下，雷诺数对喷流气动干扰的影响相对较小，高度变化带来的影响主要由压力比变化造成。通过比较发现，喷流气动干扰随压力比变化的线性度最好，因而可以利用较少的数据进行线性插值来获得全空域的喷流干扰。与传统的按高度线性插值相比，本文提出的按压力比进行分段线性插值的方法误差更小，具有较强的创新性，并已实现工程应用。在型号研制过程中，应根据喷流干扰随压力比变化的规律，划分出线性度较好的区间，选择区间边界点作为计算状态，为全空域插值提供基础数据，这样既可减少计算量，又可提高插值精度。