某双脉冲发动机压力振荡产生机理及抑制方法分析

赵 瑜，李莎莎，刘 喆，薛牧遥

(上海航天动力技术研究所，上海 201109)

0 引言

在发动机工作过程中，燃烧室受到扰动时就会产生一定振型和频率的声波。当扰动产生的压力振荡频率与燃烧室声场的固有频率一致时，将产生共振现象，即声不稳定燃烧。此时，燃烧室内压强的振荡幅值将明显放大，从而导致发动机产生剧烈的机械振动、旋转，并破坏燃烧室壳体，甚至可能引起发动机爆炸并形成灾难性后果。

目前，固体火箭发动机装药形式越来越复杂，很多发动机采用分段式装药，段与段之间存在绝热环等障碍物，使燃气在流动过程中发生分离并出现漩涡，而固体发动机燃烧室内规律性的漩涡脱落被认为是引起声涡耦合的重要原因。声涡耦合理论指出：当流场中漩涡脱落频率接近燃烧室声腔的某一阶声模态的固有频率时，就有可能激发该模态并引起声场共振，导致燃烧室内压强振荡，出现不稳定燃烧现象[1]。国内外众多学者对此现象展开过研究。如：JACOB等[2]首次提出了声涡耦合是引起固体火箭发动机不稳定燃烧的潜在诱因；DOSTON等[3]研究了Tiatan IV RSRM的推力振荡特性，建立漩涡形成、脱落、碰撞、声反馈的4步模型，为固体火箭发动机涡声耦合研究奠定了基础；CULICK等[4]通过试验证实了旋涡脱落频率与发动机声腔内的声频率可相互耦合，当两者频率接近时会出现压力振荡。文献[5-7]用P230缩比冷流试验发动机对障碍物漩涡脱落进行了大量试验研究，并开展了相应的数值模拟工作，对涡声耦合引起的压力振荡现象进行了深入分析。国内以西北工业大学和北京理工大学为主，在不稳定燃烧的理论研究、试验测试、数值模拟等方面开展了一系列研究。文献[8-11]相继对固体火箭发动机内的声涡耦合现象进行了数值模拟，研究表明：大涡模拟技术能较好地捕捉燃烧室内漩涡的运动规律及压力振荡特性，是不稳定燃烧研究的有力工具。文献[12-14]详细分析了声涡耦合压力振荡现象，研究了固体发动机工作末期不稳定燃烧的机理，并提出了头部空腔抑制压力振荡的方法。苏万兴等[15]以VKI发动机为模型，采用大涡模拟开展了障碍物旋涡脱落引起的压力振荡现象研究，通过数值模拟、试验研究与理论分析相结合，系统研究了大长径比固体发动机工作稳定性的关键增益机理与阻尼特性。

本文以某双脉冲发动机为研究对象，探寻其二脉冲工作时压力振荡大幅上升的原因，以及扰流环抑振效果的内在机理。经初步分析，发动机燃烧室声腔的一阶轴向固有频率(由经典圆柱形声腔固有频率预估公式得到)与其内部的压力振荡频率(由傅里叶变化得到)十分接近，初步判断可能是声涡耦合诱发的不稳定燃烧现象。为验证该推测，采用有限元和大涡模拟算法分别对燃烧室声腔固有频率和漩涡脱落频率进行了深入分析，并在此基础上研究了使用扰流环后带来的影响。

1 计算模型与数值算法

1.1 有限元声振型计算方法

固体火箭发动机燃烧室空腔内充满燃气，受到初始扰动时会出现各种振型的自由声振荡，在声波的传播过程中，介质质点的振动会导致局部压力和密度在稳定值附近振荡，可表示为

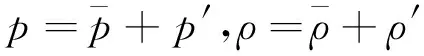
(1)

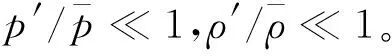
(2)

式中：a为声速。

有限元模型通用的矩阵方程为

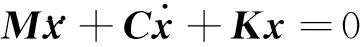
(3)

式中：M为结构质量矩阵；C为结构阻尼矩阵；K为结构刚度矩阵。为获得燃烧室空腔的振型及相应的频率，需要根据声压与声速关系，将式(2)转换为如下单元矩阵形式

(Kf-ω2Mf)p=0

(4)

式中：Kf为声刚度矩阵；Mf为声质量矩阵。使用有限元法求得声特征向量p及圆频率ω，由f=ω/2π即可求得声振频率。

1.2 大涡模拟控制方程

在声涡耦合诱发固体发动机不稳定燃烧的研究中，漩涡脱落频率的计算十分关键，因而需要采用大涡模拟的方式对发动机内部的湍流状态进行高精度求解。大涡模拟的控制方程可通过对原始N-S方程进行空间滤波后得到，以流动参数f为例，其空间滤波被定义为

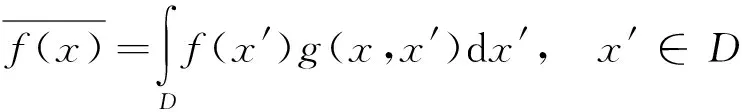
(5)

式中：D为积分区域；g为滤波函数。对于不可压流，经空间滤波后的N-S方程为

(6)

(7)

2 发动机压力振荡现象分析

2.1 发动机结构特点

发动机二脉冲为内孔燃烧加局部端面燃烧。二脉冲工作初期发动机空腔模型如图1所示。

图1 发动机燃烧室空腔模型Fig.1 Numerical model of motor’s combustion chamber

2.2 试验结果分析

发动机二脉冲试验过程压强-时间曲线如图2所示。从曲线中可看出发动机在工作后期出现了较为严重的压力振荡现象，在1.25 s之前发动机压强-时间曲线较为平稳，从1.25 s开始出现压力严重的压力振荡，直至发动机工作结束。

将1.25 s后发动机的振荡数据进行频域变换后，不同时间段内的振荡主频如图3所示，在1～1.25 s时刻内燃烧室压力振荡比较微弱，其振荡主频为320 Hz，对发动机工作特性几乎没有影响；当发动机工作至1.25 s，振荡幅值明显增加，1.25～1.5 s时域内的振荡主频率为314.7 Hz，随着发动机工作时间的增加，压力振荡主频率不断减小，在发动机工作末期压力振荡主频率将为284 Hz。

图2 发动机试验过程压力-时间曲线Fig.2 Pressure versus time for motor in test

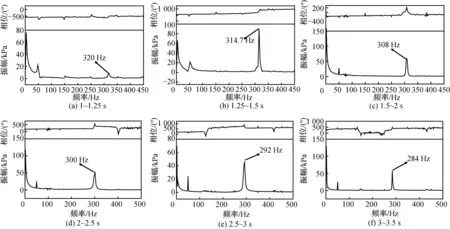
图3 试验中不同时刻发动机燃烧室压力振荡主频率Fig.3 Frequencies of motor’s pressure oscillationat various moments in test

2.3 压力振荡现象机理分析

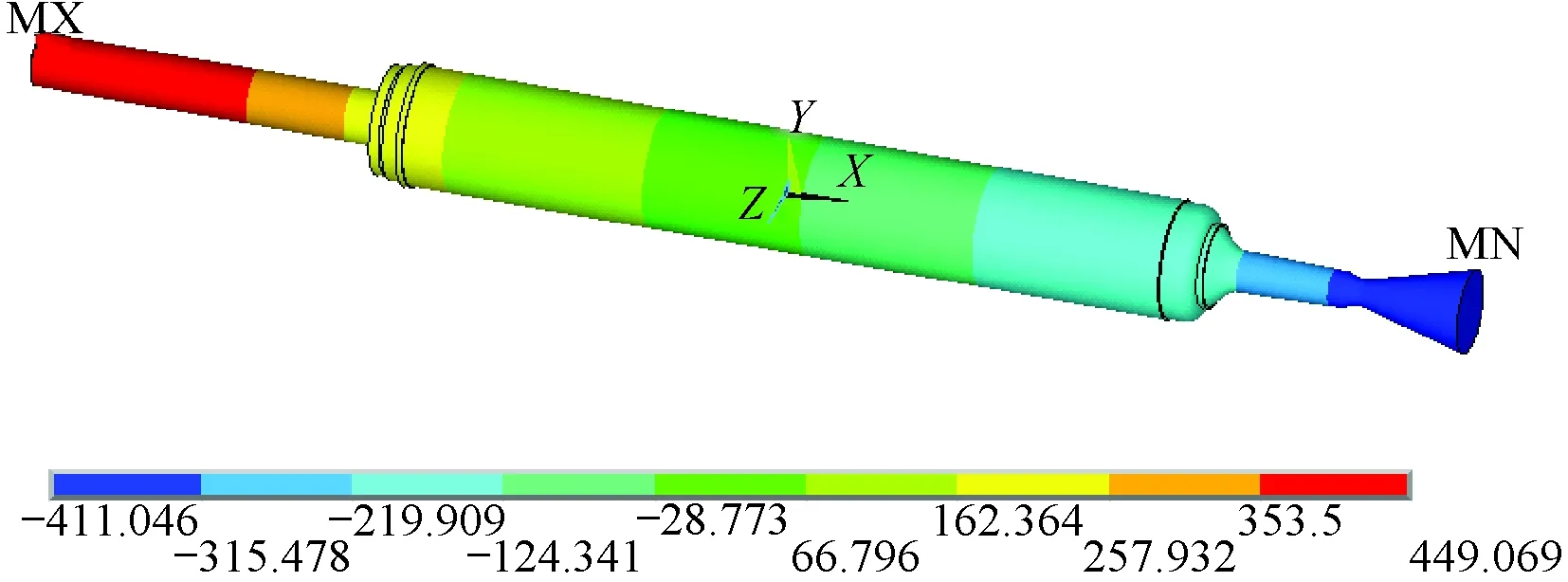
图4 发动机燃烧室空腔轴向一阶声振型Fig.4 Shape of motor chamber’s first axial acoustic model

根据药柱退移形式对不同时刻燃烧室空腔进行建模，利用ANSYS软件中的acoustic30声流体单元对不同时刻轴向一阶振型的声频进行仿真计算，模型表面定义零位移约束。初始时刻燃烧室内声介质密度为4.0 kg/m3，平均声速为1 127 m/s，计算所得初始时刻发动机轴向一阶声振型如图4所示，发动机的轴向一阶频率为351.5 Hz。采用相同方法，计算不同时刻燃烧室空腔的轴向一阶振型的声频，见表1。从表中可看出发动机燃烧室轴向一阶振型声频随着时间退移呈下降趋势，与试验过程中发动机压力振荡主频趋势一致，并且计算所得1.25 s后的声振频率与试验结果非常接近，说明发动机二脉冲工作时出现了以轴向一阶声振频率为主的不稳定燃烧。

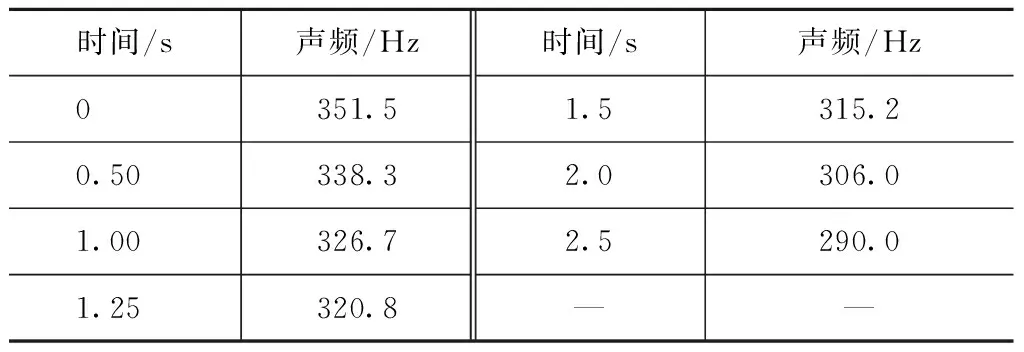
表1 不同时刻发动机轴向一阶振型声频

利用大涡模拟对不同时刻发动机燃烧室内的流动状态进行求解时，需要对网格无关性进行考察。考察结果如图5所示。当网格数量达到3.0×105以上时，计算得到的压力振荡主频率已基本保持不变。因此，计算中最终采用的网格量级为3.0×105左右。经数值模拟，发动机燃烧室内的漩涡脱落现象如图6所示。从图中可见，二脉冲装药的后向台阶是漩涡脱落的主要原因。该漩涡沿轴向不断向下游发展，并最终在喷管收敛段与管壁发生碰撞。同时，由图4可知，压力监测点1正好处于纵向一阶声振型的波腹，因此其声压振幅较大。所以，后续的数据处理主要针对压力监测点1，并将处理得到的燃烧室压力振荡主频率列在表2中。从表2中数据可见，发动机燃烧室内漩涡脱落形成的压力振荡主频率同样随时间推移不断下降。

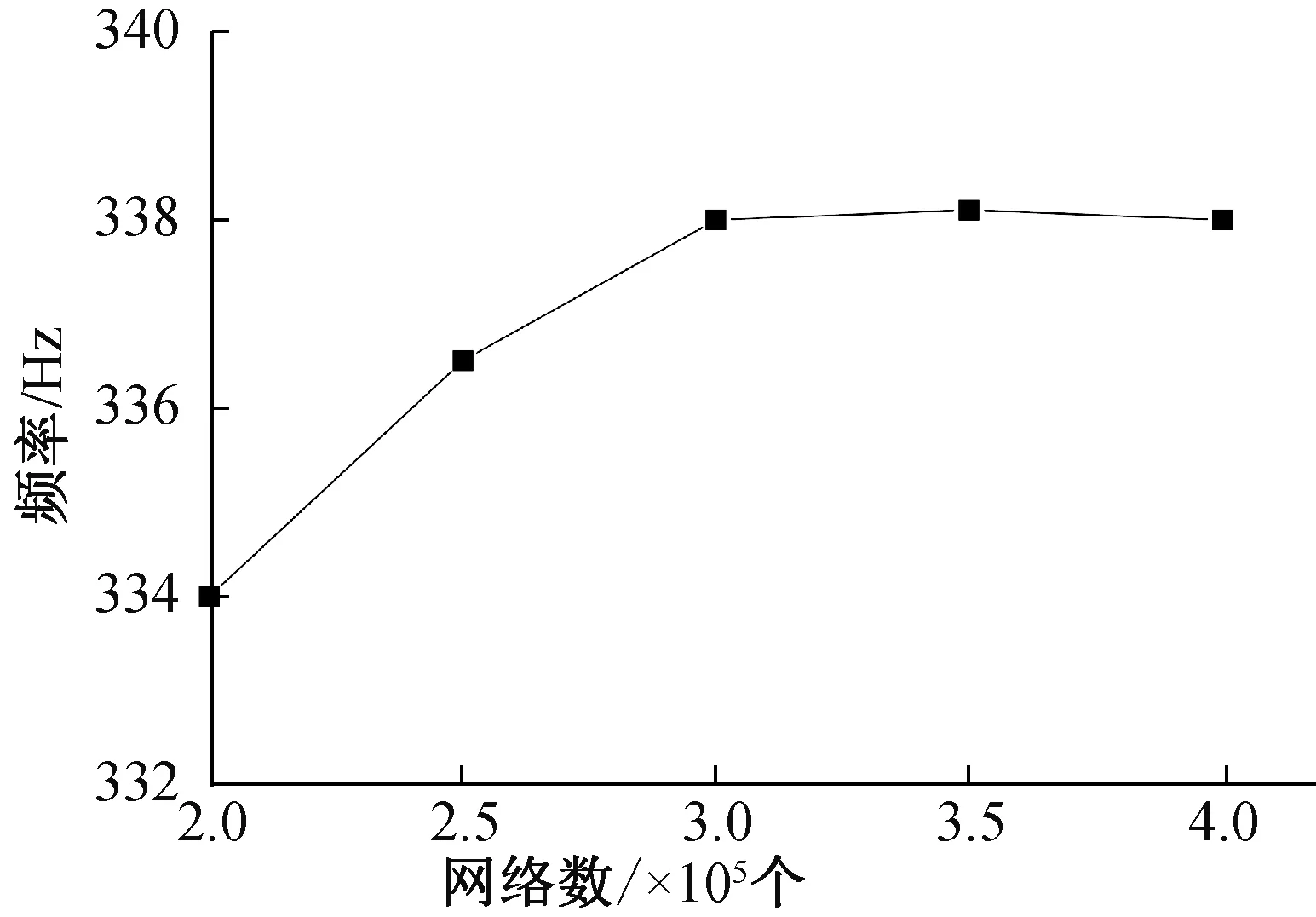
图5 压力振荡主频率与网格数量间的关系Fig.5 Relationship between pressure vibration’s frequency and mesh number

图6 发动机燃烧室内的漩涡脱落Fig.6 Vortex-shedding in motor chamber

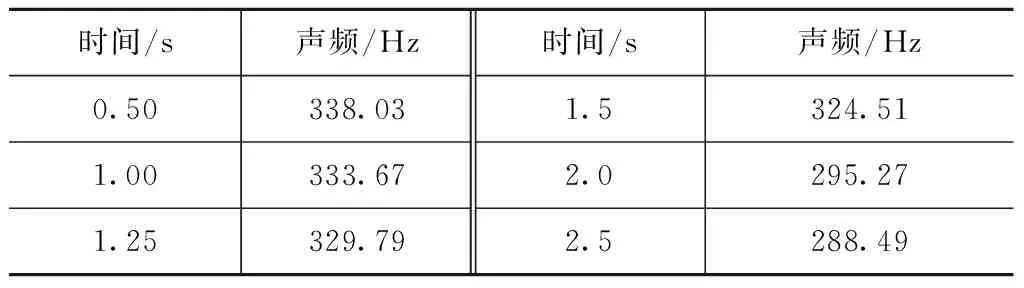
时间/s声频/Hz时间/s声频/Hz0.50338.031.5324.511.00333.672.0295.271.25329.792.5288.49

图7所示为各个时间段内试验测得的燃烧室压强振荡主频、燃烧室空腔一阶轴向声振频率和漩涡脱落形成的压力振荡主频三者之间的对比。从图7中可见，三者十分接近。因此，可以基本确定发动机工作时发生的压力振荡现象由声涡耦合引起，即由于燃气流经二脉冲药柱的后向台阶结构后形成了漩涡脱落，而该漩涡脱落的频率与发动机空腔的轴向一阶声振频率十分接近，从而形成了自激声振荡即声不稳定燃烧现象。而且试验中压力振荡现象发生后，压力振荡频率持续下降的原因主要是由于空腔声振频率和漩涡脱落形成的压力振荡主频同时下降造成的。

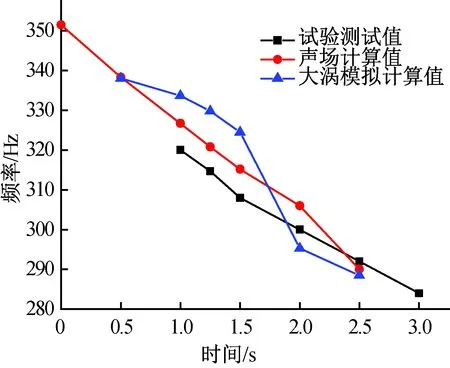
图7 发动机各组频率间的比较Fig.7 Comparison for various groups of frequencies

3 扰流环抑制压力振荡现象的机理分析

图8 不同通径扰流环下试验过程的压力-时间曲线Fig.8 Pressure versus time for motors using various flow-disturbing rings

为抑制发动机二脉冲压力振荡现象，在发动机一脉冲与二脉冲之间增加了扰流装置，并对扰流装置抑制压力振荡现象进行了试验验证。试验结果表明：当扰流环中心通径为95 mm时，试验结果无振荡；当扰流环中心通径为105 mm时，试验结果基本无振荡；当扰流环中心通径扩大为115 mm时，试验出现振荡。不同通径的扰流环消振试验过程的压力-时间曲线如图8所示。

针对试验中采用的3种不同通径的扰流环，建立带扰流环结构的发动机燃烧室空腔模型，如图9所示。对发动机二脉冲工作时的声腔频率和压力波动频率进行了计算，分析其抑制压力振荡的原理，并探索扰流环结构自身参数变化时对压力振荡的影响规律。

图9 带扰流环结构的发动机燃烧室空腔模型Fig.9 Numerical model of motor’s combustion chamber with flow-disturbing ring

图10为中心孔径Φ95 mm扰流环形成的漩涡结构。由于扰流环的存在，燃气在经过扰流环时会形成漩涡，漩涡在往下游移动过程中体积不断增大。

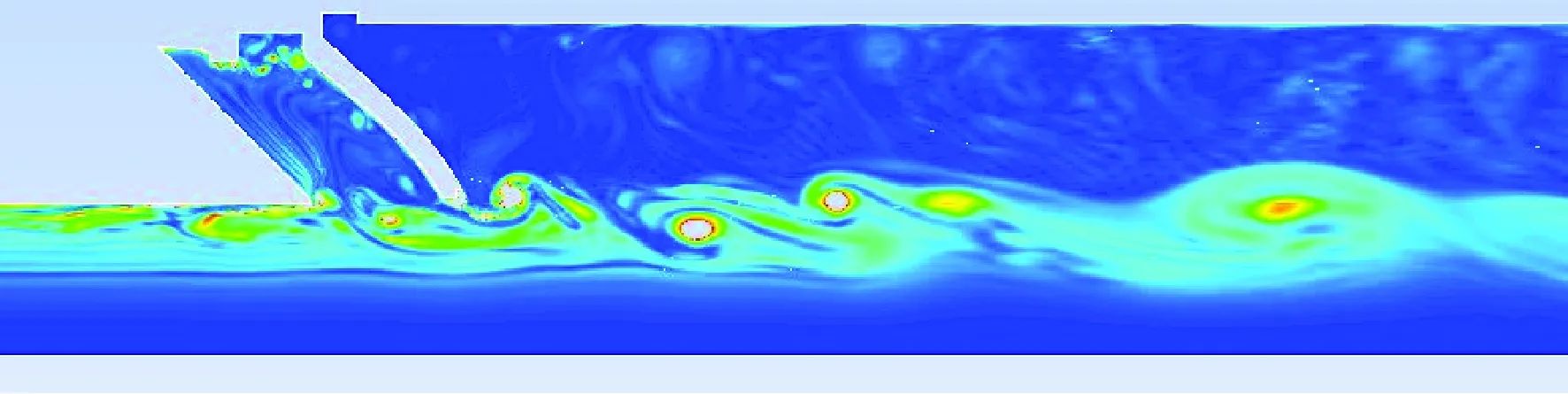
图10 中心孔径Φ95 mm扰流环形成的漩涡结构Fig.10 Structure of vortex shedding with flow-disturbing ring(Φ95 mm in diameter)

将带3种尺寸扰流环结构的发动机在不同时刻的声腔频率、大涡模拟频率与原发动机声腔频率、大涡模拟结果进行对比，如图11所示。

图11 原发动机与带不同通径扰流环 发动机各组频率间的比较Fig.11 Frequency comparison between motors with and without flow-disturbing ring

扰流环的存在并没有明显改变发动机的轴向一阶声频，但却使发动机工作初期的漩涡脱落频率得到明显提高，扰流环通径越小发动机的漩涡脱落频率越大，即发动机工作初期的漩涡脱落频率与发动机燃烧室空腔的轴向一阶声频差别越大，从而避免了压力振荡现象的出现，这一结论与发动机的试验结果相吻合，见表3。

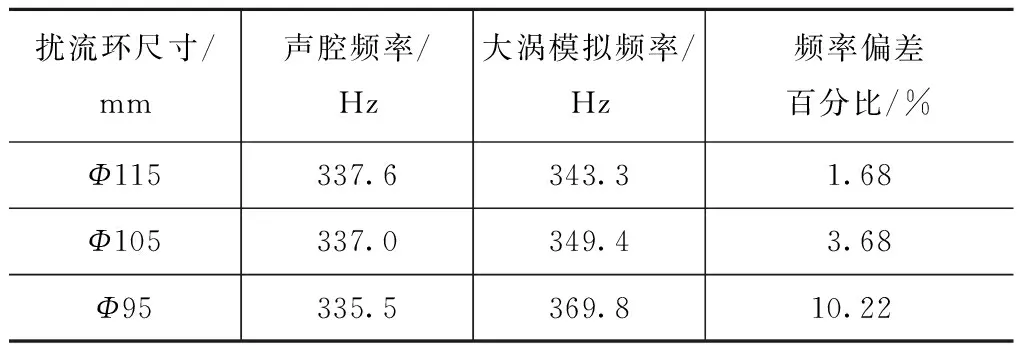
表3 不同扰流环尺寸下发动机工作初期(0.5 s时)的频率对比

4 结束语

本文采用声腔有限元及大涡模拟技术，对双脉冲发动机二脉冲工作过程中的压力振荡产生原因及抑制机理进行了研究。研究发现发动机二脉冲工作过程中出现的压力振荡现象主要由声涡耦合引起，当燃气流经二脉冲药柱的后向台阶结构后形成了漩涡脱落，而该漩涡脱落的频率与发动机空腔的轴向一阶声振频率十分接近，从而形成了自激声振荡现象；扰流环对压力振荡的抑制作用是由于其提高了发动机工作初期的漩涡脱落频率，扰流环孔径越小漩涡脱落频率越高，使该频率远离了发动机空腔的轴向一阶声频，从而抑制了压力振荡的形成。需要说明的是：当声涡耦合为主要诱因时，文中采用的不稳定燃烧分析方法是科学和有效的。所以，它对固体发动机设计工作具有较好的指导意义，特别是在装药设计和不稳定燃烧抑制手段的验证方面。但该方法在使用过程中并没有考虑两相流的影响，而凝相颗粒在压力振荡的抑制上有时又发挥着十分重要的作用。因此，后续研究需要加入这部分内容，以使计算模型更加逼近真实情况。