Exploring Channel Diversity in HF Communication Systems: A Matching-Potential Game Approach

Wen Li, Lang Ruan, Yifan Xu, Yuli Zhang, Yitao Xu,＊, Xinhong Shao

1 College of Communications Engineering, Army Engineering University of PLA, Nanjing 210000, China

2 Science and Technology on Communication Networks Laboratory, Shijiazhuang 050000, China

Abstract: This paper investigates the channel diversity problem in high frequency (HF) communication systems. Due to the limited HF spectrum resources, a HF communication system with shared channels is considered, where each user equipment (UE) has individual communication demand. In order to maximize the communication probability of the whole system, a matching-potential game framework is designed. In detail, the channel diversity problem is decomposed into two sub-problems.One is channel-transmitter matching problem,which can be formulated as a many-to-one matching game. The other is the transmitter allocation problem which decides the transmission object that each transmitter communicates with under channel-transmitter matching result, and this sub-problem can be modeled as a potential game. A multiple round stable matching algorithm (MRSMA) is proposed,which obtains a stable matching result for the first sub-problem, and a distributed BR-based transmitter allocation algorithm (DBRTAA)is designed to reach Nash Equilibrium (NE)of the second sub-problem. Simulation results verify the effectiveness and superiority of the proposed method.

Keywords: HF communication; channel diversity; game theory; many-to-one matching game; potential game.

I. INTRODUCTION

High frequency (HF) communication is an important way in wireless communication. With the advantages of no relay transmission, long communication distance and strong survivability,HF communication plays a significant role [1] in military and civil field. However, HF channels are very complex and unstable, containing many disadvantages. First, the channel characteristic is time-varying. Second, there exists complex interference and jamming such as natural interference and malicious jamming. Therefore, ensuring the reliability and stability of HF communication is important but challenging.

The researches on HF communication mainly focused on channel modeling [2, 3] and new methods to achieve reliable data transmission[4] [5]. However, the resources allocation problem, which is discussed widely in mobile communication, has been rarely considered in HF communication systems. As the communication resources are limited, it should be considered how to allocate the resources under the circumstance that the user equipments (UEs) have to compete for resources.

In HF communication systems, channel diversity is widely used to improve transmission reliability. Channel diversity means that the transmitter will transmit signals via sev-eral channels, and the UE receives signals via multiple channels. Once the UE demodulates signal correctly in more than one channel, it is considered that the signal transmission is successfully completed. Unlike traditional mobile communications, channel diversity consumes more channel resources to improve transmission reliability in HF communications.

The channel diversity scheme in existing HF communication systems is to assign available channels to all UEs uniformly without duplication. For example, when there are 80 available channels and 20 UEs, each UE is assigned four channels uniformly. When the number of channel diversity is determined, the number of UEs which can access in the system is limited. Although such channel diversity scheme can avoid co-channel interference,it is not effective when the scale of UEs are large. Although there are few works concerning about the channel diversity in HF systems,there exists many researches focusing on channel resources allocation and channel selection[6-9][14]. Different from mobile networks, the HF channels with electromagnetic wave reflection are more unstable and time-varying, and the transmission distance of HF communication is about dozens to hundreds of kilometers.Therefore, the reliable communication links in HF systems are more dif ficult to built, and the channel diversity is necessary to improve the communication probability in HF systems.The channel resources allocation in mobile networks mainly discuss system throughput or interference elimination. However, in HF communication systems, we pay great attention to obtain higher communication probability using better channel allocation, which is an evaluation for the UE to realize reliable communication.

An effective channel diversity optimization should be conducted so as to achieve higher communication probability for the whole HF system. Nevertheless, solving the channel diversity optimization problem is challenging due to the enormous strategy space. The game models are powerful and promising to address the resource allocation problem [10,11].Therefore, we propose a matching-potential game framework to investigate the channel diversity problem.

In this paper, the problem of channel diversity in HF communication systems was studied, which was modeled as a matching-potential game to maximize global communication probability.

For the sake of solving the channel diversity problem, it is decomposed into two sub-problem: The first one is a channel matching problem, that is, to find a transmitter-channel matching scheme which can achieve higher expected throughput for all UEs in the HF system; The second sub-problem is a transmitter allocation problem, that is, under optimal transmitter-channel matching scheme, and each user is allocated with several transmitters, so as to achieve highest communication probability. Moreover, the first sub-problem can be formulated as a many-to-one matching game between transmitters and channels [12-13], which can obtain a stable solution via distributed matching algorithm [15-17]. The second sub-problem can be regarded as a potential game from the UEs’ perspective, which can be proved to be an exact potential game(EPG), and the existence of Nash Equilibrium(NE) of the EPG can be proved as well.

The main contributions are summarized as follows:

• The problem is decomposed into two sub-problem, where the first one is formulated as a many-to-one matching game and the second one is formulated as a potential game.

• The theoretical analysis of the many-toone matching game as well as the potential game is presented, a multiple rounds stable matching algorithm (MRSMA) and a distributed BR-based transmitter allocation algorithm (DBRTAA) are designed for obtaining game solutions. Moreover, convergence and the performance of the proposed approach are presented.

The rest of the paper is organized as follows. In Section II, the system model is established. The game theoretic framework of the channel diversity problem is analyzed in section III. In section IV, the simulation results are presented, and the rationality of the results is investigated. Finally, the conclusion is shown in section V.

II. SYSTEM MODEL AND PROBLEM FORMULATION

we investigate a HF communication system consisting of a certain number of stations,and all stations can interact with each other through the gateway. Each station is equipped with a certain number of transmitters, which is able to transmit data to UEs through HF channels. We consider the downlink transmission process where the stations transmit data to UEs. Denote the set of transmitters as M, i.e., M={1,2,…,M}, and the set of HF channels as F={1,2,…,F}. Assume there are N UEs being served in the HF system and denote the set of them as N, i.e.,N={1,2,…,N}. Besides, the set of data traffic requirements of UEs is denoted as P = { p1, p2,… ,pn,… pN},0 ≤pn≤1. Specially, pn=0 represents there is no data traffic requirement in UE n.

Channel diversity is adopted to enhance the down-link transmission reliability for the HF communication system, which can receive the same signal from multiple channels. Let θm,f,ndenotes the available probability when

2.1 System model

transmitter m sends data to UE n using channel f. Hence, the three-dimensional matrixrepresents all the channel available probability1In this paper, the channel available probability is assumed to be fixed.As an improvement,in our on-going work,the probability matrix is constructed by actual data measured in HF channel. when different transmitters and UEs are communicating through a certain channel.. An example of the proposed HF communication system model is shown in figure 1, which involves four UEs and nine transmitters. It is shown that based on channel availability probability θ, the data transmission process may be interfered when the channel is reused among UEs and transmitters.

Furthermore, we characterize the communication selection strategy profiles as, w h e r e δm,f,n=1 indicates that transmitter m transmits to UE n through channel f transmission (link m− f−n), while δm,f,n=0 means the transmission link m−f−n is not available. For example, as shown in figure 1, we have δ1,1,1=1,δ2,2,4=1, δ3,3,2=1, δ4,2,1=1, δ5,4,2=1,δ6,5,4=1, δ7,1,2=1, δ8,3,3=1 and δ9,5,3=1, while others in δ are all equal to 0. The number of possible strategy selection profiles is(), where k is the number of channel diversity. For example, when one HF system contains 12 transmitters, 6 UEs, 10 HF channels and k is 3, the number of possible strategy selection profiles is about 1.1338e+26. The channel diversity problem is challenging due to the enormous strategy space.

2.2 Problem formulation

It is assumed all transmitters can sense all channels, but can only transmit data traffic through one channel, a collision may occur when two or more transmitters are transmitting simultaneously on the same channel. The channel availability probability θm,f,ncan be used as transmitter selection judgment for one channel. Hence, the transmitter decision function f(θm,f,n,θm1,f,n) is defined as:

Therefore, the transmission probability of link m−f−n can be expressed as follows:

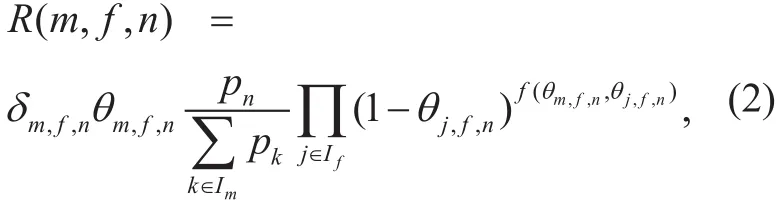
where Imrepresents all the UEs which select transmitter m, i.e.Im={n ∈ N :δm,f,n= 1, f ∈F}, Ifrepresents all the transmitters which select channel f, i.e.If={m ∈ M:δm,f,n=1,n ∈N }. Transmission probability R( m, f, n) is an evaluation of transmission link m−f−n, which reflects the probability that transmitter m can communicate with UE n successfully via channel f.

According to Eq. (2), the transmission probability of global system is given by:

Hence, the global objective of channel diversity optimization problem is to find the optimal transmitter and channel selection profiles for UEs to maximize the system’s transmission probability, i.e.,

However, solving problem P is extremely challenging due to the huge strategy space,which motivates us to design a matching-potential game framework to solve it.

III. A MATCHING-POTENTIAL GAME FRAMEWORK FOR CHANNEL DIVERSITY

In this section, the matching-potential game framework for the channel diversity optimization problem is shown. Moreover, the dimensionality reduction solving process and game solutions are also presented.

3.1 Dimensionality reduction solving process

Note that solving the channel diversity optimization problem P is challenging due to the enormous strategy space, a dimensionality reduction method is considered by dividing P into two subproblems: channel matching and transmitter allocation. The step design and the analysis are given in the following. Suppose that UE n is equipped with a set of transmitters mn∈M, and transmitter mnchooses a channel fm∈F for transmission, then we have δm,fm,n=1,m∈mn, indicating transmission link m−f−n is available. Specifically,denote A1mand A2nas the set of fmand mnrespectively, m∈M, n∈N.

Step 1→Channel matching:

Since the UE selection strategy has not been determined for transmitters, we consider the whole HF system and denote the expected throughput rmas follows:

where rmrepresents the whole HF system’s expected throughput which transmitter m can provide through channel fm.

Then, according to Eq. (6a), the channel matching problem is to find an optimal transmitter-channel matching scheme which can achieve higher expected throughput for all UEs in the HF system:

Step 2→Transmitter allocation:

Under optimal transmitter-channel matching scheme, calculate optimal transmitter allocation strategy for transmitters, so as to achieve the highest transmission probability of the whole system. Therefore, we have the following equation:

Finally, the solutions of sub-problem P1 and sub-problem P2 constitute the solution of P. Proof work will be performed in the next section that both P1 and P2 can be solved and have optimal solution.

Since there is no centralized controller available for the proposed model, and both problem P1 and P2 are discrete optimization problems which are NP-hard [18]. A matching-potential game [19] framework is adopted for the channel diversity optimization problem. The specific schematic of channel diversity optimization scheme is shown in figure 2. In the following, we will analyze the two subproblems separately.

3.2 Channel-transmitter matching game

In this subsection, we propose a channel matching game to solve the sub-problem P1.In P1, the channel-transmitter matching problem is mainly investigated. As is known, the channel allocation strategy space is FMfor all transmitters, which is extremely huge with a big F or M. Thus, it is hard to solve problem P1 via a centralized approach, which motivated us to explore the solution using a distributed scheme.

The game theory can effectively solve the distributed resources allocation optimization problem [20-25]. Therefore, we model the problem P1 as a channel matching game. The matching parties are transmitters M and HF channels F. As it is assumed that one transmitter can only occupy one channel, and each channel can be assigned to multiple transmitters. A many-to-one matching game model is suitable to model the problem P1 in HF communication system. The definition of the many-to-one matching game is as follows:

Definition 1. A many-to-one matching µis defined as a mapping from the set M∪F into the set M∪F and two preference relations ≻mand ≻f. 1) µ(f)∈M and|µ(f) |∈ {1,2 …,qc} for each HF channel. 2)u( m)∈F and |µ(m )|= 1 for each transmitter.3) f∈µ(m) if and only if m∈µ(f).

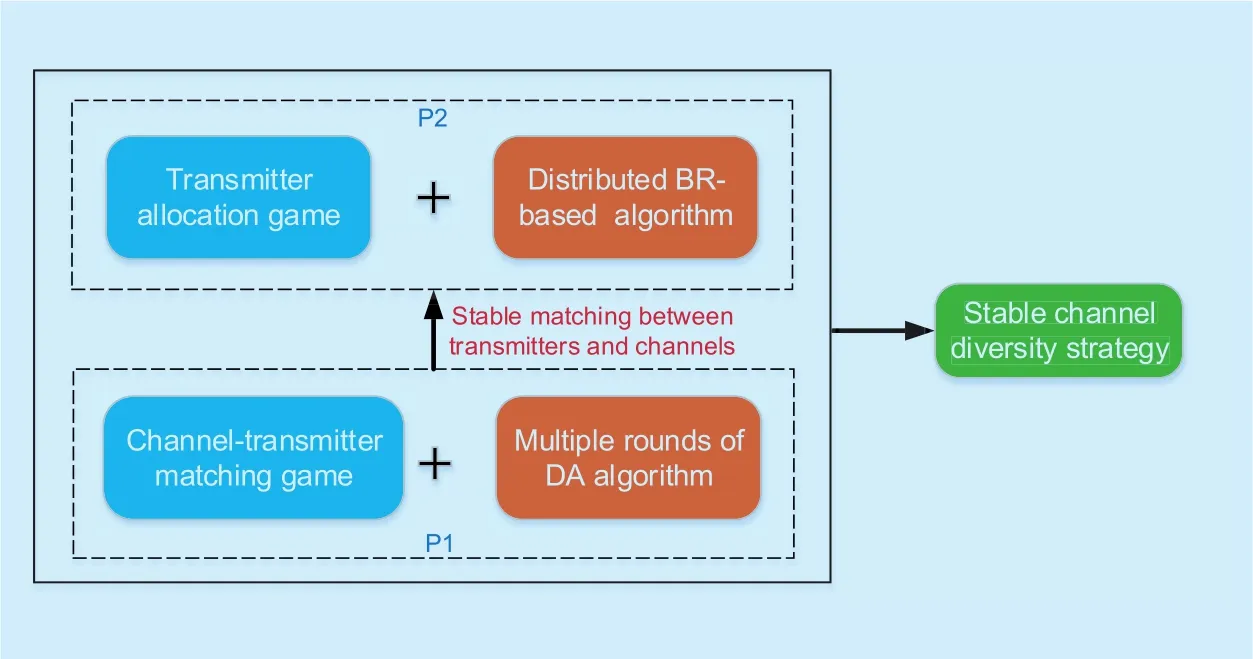
Fig. 2. Solving process flow diagram.

Preference relations ≻mand ≻frepresent transmitter m’s channel preference relation and channel f’s transmitter preference relation, respectively. µ(f) means the subset of transmitters using channel f, and µ(m) means the subset of HF channels which is accessed by transmitter m. The quota is the maximal number of transmitters each channel can match, which can be denoted byandmeans ceil. The final constraint ensures that the matching is the mutual consent between transmitters and HF channels. Therefore, the matching game can be defined as a tuple:

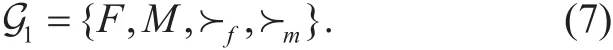
To describe the matching μ, we define the preferences by two sides of the game

1) For transmitter preferences: In HF communication system, each transmitter m seeks to find the channel with higher throughput according to (5). For two channels f1m,f2min the channel strategy space A1m, the preference of each transmitter m can be expressed as:

where rm(f 1m), rm(f2m) represent the average throughput of transmitter m under channel f1mand f 2m. Therefore, the channel which can provide higher average throughput will obtain higher priorities. The channel which can provide same average throughput to transmitter m will have the same priority.

2) For HF channel preferences: In HF communication systems, each channel f seeks to find transmitter with higher throughput so as to improve the system communication probability. For two transmitters m1, m2 in the available transmitter set, the preference of each channel f can be expressed as:

where rm1(f ), rm2(f) represent the average throughput of transmitter m1 and m2, when they use channel f. Therefore, the transmitter which can provide higher average throughput will obtain higher priorities. The transmitters which can provide same average throughput with channel f will have the same priority.

Definition 2. In each round, a matchingµ is stable, if and only if ∄m, n∈N, s.t.µ(n) ≻mµ(m) and m≻µ(n)n .

A channel matching algorithm based on the traditional deferred acceptance (DA) algorithm[30] is proposed to solve the channel matching problem. Preference lists for transmitters and HF channels can be fixed in the matching process. When the number of transmitters is larger than the number of HF channels, we consider to use a multiple rounds stable matching approach. In each round, there are two main stages: unmatched transmitters make a request and HF channels accept or reject. The specific process is shown in Algorithm 1.

Theorem 1. In each round, the proposed algorithm is guaranteed to converge to a local stable matching.

Proof: As the number of transmitters and HF channels is limited in each round, the preference lists of transmitters and channels are finite.All transmitters will be matched, because the number of channel is not less than the number of transmitters. when all transmitters are matched, we assume two different transmitter n and m which match to channel fnand fmrespectively, and satis fies fm≻nfn. In the matching process, each channel accepts its favorite transmitter after each request round. Therefore,we have fm≻nfnand m≻fmn, ∀m, n∈M.In each round, the matching is stable.

3.3 Transmitter allocation game

Given the transmitter-channel matching scheme from solving P1, transmitter allocation mechanism is proposed to determine the transmitter allocation for UEs. Note that the transmitter allocation mechanism is distributed because UEs interact with each other and make self-determined transmitter selection.This motivates us to formulate the problem as a potential game, which requires players take cooperative control in distributed multi-agent systems and achieve global objective through individual utility of each player.

?

The transmitter allocation problem is formulated as a strategic form game, which is characterized by the following elements: (1) A UE set N={1,2,…,N}. (2) A action profile set{A2n}n∈N, where mn∈ A2nis a transmitter selection strategy set of UE n due to channel diversity mechanism. (3) A utility function set u2n(mn, m−n), where m−nis the action profiles of all the UEs except n. Inspired by [27], we define the utility function based on transmitter allocation game as follows:

where Rk(mk, m−k) is UE k’s communication probability, defined as:

Jnis the UEs which choose the same transmitter as UE n and may cause interference to UE n. it can be expressed as:

where mnand mn′ mean the current selection strategy, and the prepared selection strategy of n, respectively. Only UEs in Jncan in fluence the communication probability of UE n. Thus,it can be found that,

Then, (10) can be simplified as

u2n(mn, m−n) represents the transmission probability of all UEs in, which is determined by UE n’s transmitter selection only.Thus, then the optimization object of the proposed game is:

according to object O2, the optimal individual utility of UE n was determined by n’s action profiles, i.e., transmitter allocations.

Definitions are given in the following to analyze the properties of the transmitter allocation game.

De finition 3. Nash Equilibrium (NE) [27]A state selection profileis a pure strategy NE of gameif and only if no player n can improve its utility by changing its action unilaterally, i.e.,

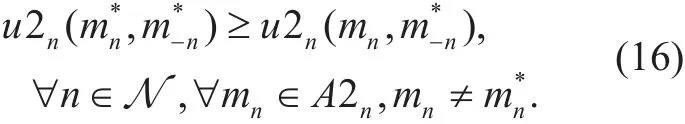
Definition 4. Exact Potential Game[29] For utility functions in a game, if there exists a potential function φ:A2→R, for arbitrary strategy selection changes from mnto mn′, the following equation is true:

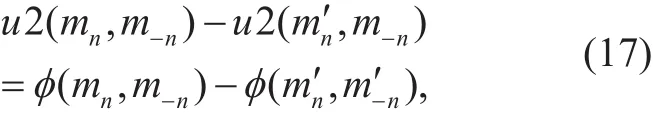
then this game is called exact potential game(EPG) and has at least one NE point.

Theorem 2. The transmitter allocation game G2 is an EPG, and has at least one pure strategy NE point. In addition, the optimal solution of transmitter allocation P2 is the pure strategy NE point of O2.

Proof: The following proof follows the lines given in [29]. we construct the whole communication probability as potential function, that is:

Suppose that an arbitrary UE n changes its action profiles from mnto mn′ in one step move, we calculate the change of the potential function caused by individual strategy selection as follows:

Intuitively, for each UE k ∈N Jn, its individual utility is completely unaffected by above action changes, thus the result of the last item from Eq.(19) is identically zero. The change of the utility function caused by individual strategy selection as follows:

In that case, combining from Eq.(19) and Eq.(20) yields the following equation:

which satisfies the characteristic of EPG according to definition 3. Thus, the formulated transmitter allocation game G2 is proved to be an EPG. According to [29], the properties of the EPG can be given, 1) Potential game has one pure Nash equilibrium(NE) at least; 2)Local or global maxima of potential function constitutes a pure NE. Therefore, the transmitter allocation game G2 has at least one pure strategy Nash equilibrium point. Furthermore,the designed potential function refers to whole coverage utility, indicating that the optimal solution of P2 turns to be the pure strategy NE point of O2.

3.4 Distributed BR-based transmitter allocation algorithm(DBRTAA)

In order to get the strategy NE point, the distributed best response(BR)-based[28] transmitter allocation algorithm (DBRTAA) is proposed in Algorithm 2, which consists of two steps: Utility computation of transmitters and Strategy evaluation.

Firstly, every UE chooses its transmitter strategy randomly. Then, for a random UE n, it finds the best strategy mn*according to (22) in stage I. In stage II, the UE n decides whether accept or not with the new strategy according to (23).

Theorem 3. With a suf ficiently large β, the global communication probability maximization can be achieved with an arbitrarily high,when the channel matching is given.

Proof: As the transmitter allocation problem has been formulated as an EPG, the optimal transmitter allocation strategy can get the maximal value of potential function in (18).With a large β, the probability to get the optimal transmitter allocation strategy converges to 1. For avoiding unnecessary repetition,the specific proof is not presented but can be found in [27].

IV. SIMULATION RESULTS AND DISCUSSION

4.1 Simulation scenario

In this section, the simulation results are shown. As shown in figure 3, HF stations and UEs are randomly distributed in a 500× 500 kilometre network topology. Each station is equipped with several transmitters.

In the simulation, we mainly consider two different scenarios: small-scale scenario and large-scale scenario. Different scenarios contain different number of transmitters, channels and UEs. The transmission power is same for each transmitter. All channel available probability and the data traffic requirements are known, and the number of channel diversity for UEs is fixed. To make a tradeoff between exploration and exploitation, β=k is chosen in Eq. (23), where k means the iteration in Algorithm 2. All results are obtained by simulating 300 times independently and then taken the average value.

4.2 Convergence performance

?

Fig. 3. The HF communication network topology of the simulation.

After getting a stable channel matching result via Algorithm 1, the global communication probability can be obtained. The results in figure 4 are tested in small-scale scenario with four transmitters, three channels and three UEs.The global communication probability is increasing as the number of iterations increases.The Algorithm 2 converges to a stable result,which is more than 90 percent of the optimal one. The result is acceptable, and the final channel diversity strategy is reliable as well.

The relationship between the cumulative distribution function (CDF) and the conver-gence iterations of Algorithm 1 is shown in figure 5. The simulation results are calculated by 1000 independent experiments in the large-scale network with 40 channels. The convergence iterations increase as the number of transmitters increases, for there are more matching con flicts. The Algorithm 1 can get a stable match, and the convergence iterations are no more than 30.

Fig. 4. Evolution results of communication probability with four transmitters, three UEs and three channels.

Fig. 5. The convergence performance of Algorithm 1 for channel-transmitter matching with diverse UEs in the HF communicaiton system with 40 channels.

Figure 6 shows the relationship between cumulative distribution function (CDF) and the convergence iterations of the distributed BR-based transmitter allocation algorithm(DBRTAA). The simulation resluts are calculated by 600 independent experiments in the small-scale scenario with 12 transmitters and 10 channels. From the figure, the average convergence iterations increase as UEs increase,for the increase in the number of UEs leads to more channel resources allocation con flicts in the system. Since the strategy space is so huge, the optimal result is hard to be obtained via the exhaustive method. The proposed approach can achieve a good global communication probability and convergence iterations are not huge.

4.3 Communication probability performance

The average communication probability level of the global system is defined aswhereis the global communication probability, and N is the number of UE. The high value ofmeans high performance of communication probability. In order to observe the communication probability, the effect of different numbers of transmitters are simulated.Figure 7 shows the performance comparison of the proposed algorithm and the exhaustive method by changing the number of UEs in the small-scale scenario, with four transmitters and three channels. As the number of UEs increases, the average communication probability continues to decrease, for there are more channel allocation conflicts in the system. Meanwhile, the result using the proposed algorithm is more than 90 percent of the optimal value. When UEs are more than six,the strategy space is so huge. It is hard to get the optimal result via exhaustive method but easy for the proposed approach to get the good strategy. We can also get the average communication probability in the large-scale scenario, with 20 channels, as shown in figure 8.The increase of UEs brings the worst average communication probability for fixed number of transmitters. More transmitter resources can bring higher average communication probability with fixed UEs.

The average communication probability under the small-scale scenario with three channels, three UEs and different number of transmitters is shown in figure 9. As the number of transmitters increases, the average communication probability in the system increases as well, since more transmitter resources can be chosen by UEs. The result using the proposed algorithm is also more than 90 percent of the optimal value. When UEs are more than seven, it is hard to find the optimal result via exhaustive method. The proposed approach can get the reliable strategy with large number of transmitters shown in figure 10. The increasing number of transmitters brings better average communication probability for fixed number of UEs. More UEs can bring worst average communication probability with fixed number of transmitters. For large-scale scenario, a good strategy can be found via the proposed approach.

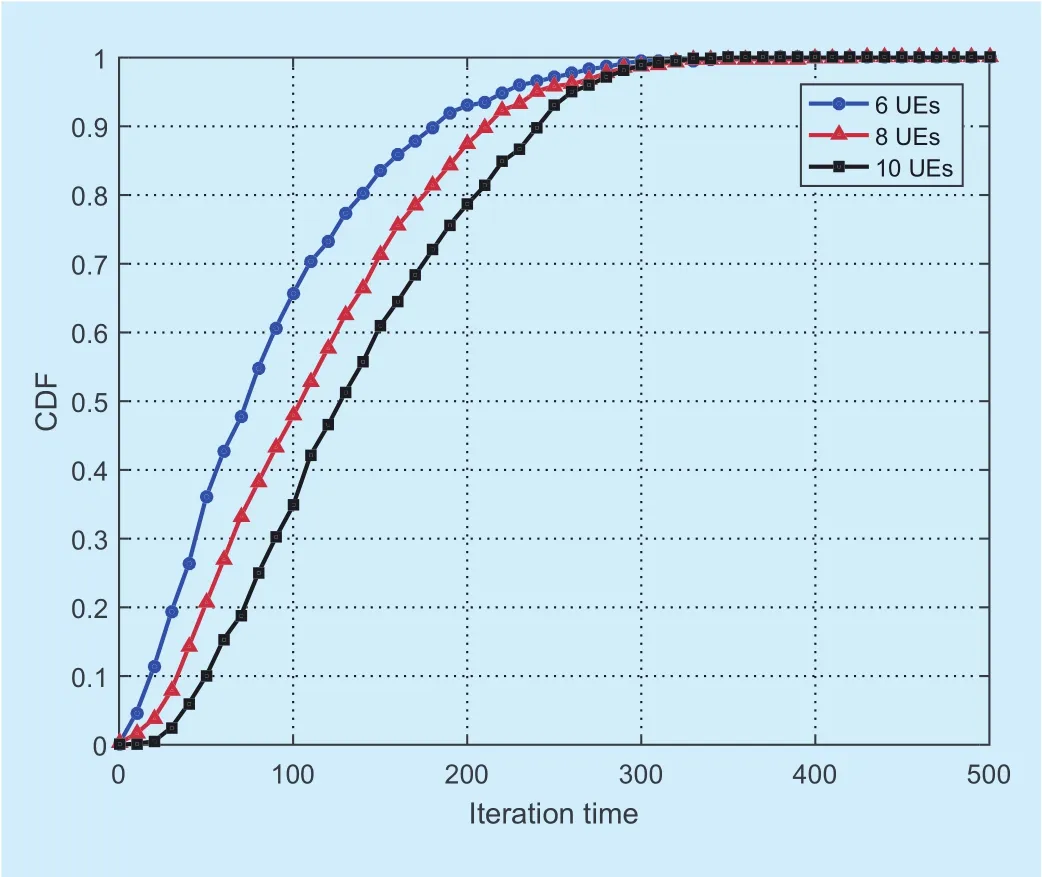
Fig. 6. The convergence performance of Algorithm 2 for transmitter allocation with diverse UEs in the HF communicaiton system with 12 transmitters and 10 channels.

Fig. 8. The convergence performance of Algorithm 2 for transmitter allocation with diverse UEs in the HF communicaiton system with 12 transmitters and 10 channels.

Fig. 7. The average communication probability with different number of UEs in small-scale scenario with four transmitters and three channels.

Fig. 9. The average communication probability with different number of UEs in small-scale scenario with four transmitters and three channels.

4.4 Fairness performance

Taking system fairness into consideration,Jains fairness index (JFI) [31] based on communication probability is introduced, which can be expressed as:

V. CONCLUSION

In this paper, the problem of channel diversity in HF communication systems was studied, the problem was modeled as a matching-potential game to maximize global communication probability. Due to the huge strategy space, the problem was divided into two sub-problems:the channel matching and the transmitter allocation. The first sub-problem was modeled as a many-to-one match game, and then a multiple rounds stable matching algorithm (MRSMA)was proposed. The second sub-problem was modeled as a potential game, which can be proved to be an exact potential game (EPG).A distributed BR-based transmitter allocation algorithm (DBRTAA) was designed to reach NE for this sub-problem. The proposed algorithms can achieve stable result, and they were compared with the exhaustive method. Simulation results showed that the proposed approach achieve more than 90 percent of the optimal global communication probability.

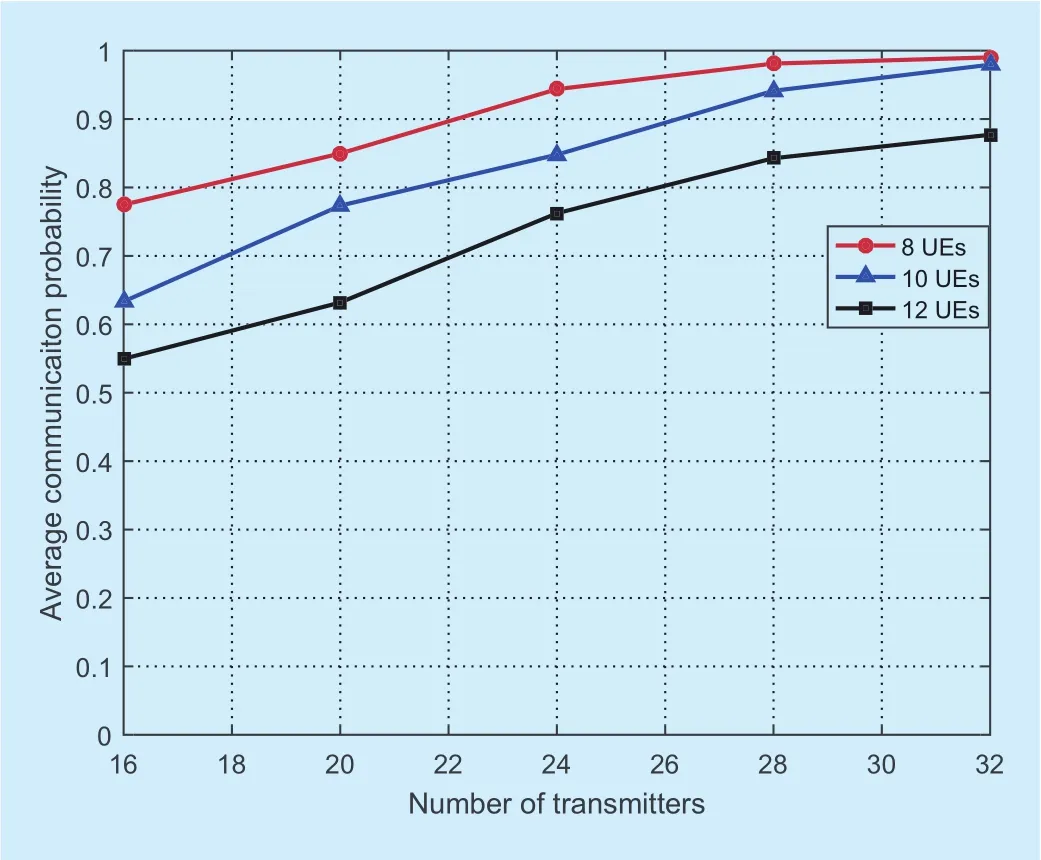
Fig. 10. The comparison of fairness performance of communication probability among UEs with heterogeneous requirements.

Fig. 11. The comparison of fairness performance of communication probability among UEs with heterogeneous requirements.

In our on-going work, the practical HF channel model will be used and the channel available probability matrix will be constructed by actual data measured in HF channel. We will think over more practical HF systems, which contain thousands of channels instead of dozens and more UEs. In practical HF systems, more factors need to be considered. Therefore, the new approaches will be found to solve the practical channel diversity problem.

ACKNOWLEDGEMENT

This work was supported by the Natural Science Foundation for Distinguished Young Scholars of Jiangsu Province under Grant No.BK20160034, in part by the National Natural Science Foundation of China under Grant No.61671473 and No. 61631020, and in part by the Open Research Foundation of Science and Technology on Communication Networks Laboratory.