Joint Non-Orthogonal Multiple Access (NOMA) &Walsh-Hadamard Transform: Enhancing the Receiver Performance

Muhammad Rehan Usman, Arsla Khan, Muhammad Arslan Usman, Soo young Shin,＊

1 Department of Electrical Engineering, The Superior College (University Campus), 55151 Lahore, Pakistan.

2 Department of IT Convergence Engineering, Kumoh National Institute of Technology (KIT), 39177 Gumi, South Korea.

3 Department of Electrical Engineering, COMSATS University Islamabad, Lahore Campus 59000, Pakistan

Abstract: Non-orthogonal multiple access(NOMA) is a new access method to achieve high performance gains in terms of capacity and throughput, so it is currently under consideration as one of the candidates for fifth generation (5G) technologies. NOMA utilizes power domain in order to superimpose signals of multiple users in a single transmitted signal.This creates a lot of interference at the receive side. Although the use of successive interference cancellation (SIC) technique reduces the interference, but to further improve the receiver performance, in this paper, we have proposed a joint Walsh-Hadamard transform(WHT) and NOMA approach for achieving better performance gains than the conventional NOMA. WHT is a well-known code used in communication systems and is used as an orthogonal variable spreading factor (OVSF) in communication systems. Application of WHT to NOMA results in low bit error rate (BER)and high throughput performance for both low and high channel gain users. Further, it also reduces peak to average power ratio (PAPR)of the user signal. The results are discussed in terms of comparison between the conventional NOMA and the proposed technique, which shows that it offers high performance gains in terms of low BER at different SNR levels,reduced PAPR, high user throughput performance and better spectral efficiency.

Keywords: Bit error rate (BER); non-orthogonal multiple access (NOMA); orthogonal frequency division multiplexing (OFDM); peak to average power ratio (PAPR); successive interference cancellation (SIC); throughput and Walsh-Hadamard transform (WHT).

I. INTRODUCTION

Today’s world telecommunication industry is shifting towards the era of future wireless networks providing the optimized solutions for consumer speed and connectivity, such as the concept of future radio access (FRA). The ease in availability of high-end consumer devices,such as smartphones and tablets etc., has given rise to intense cellular traffic growth. According to the forecast update by Cisco, the global mobile data traffic is expected to increase nearly eight-fold between the years 2015 and 2020 [1, 2]. With this growth rate comes the demand of high data speed, throughput and network capacity. To cope with this, the network operators are compelled to continuously look for new solutions and possibilities for meeting the high-end consumer requirements.With the advancement towards FRA and to go beyond 5th generation (5G) technologies,researchers are working to provide long term solutions for achieving high-end throughput.One of such recently proposed solutions is the use of power domain non-orthogonal multiple access (NOMA) technique, that can achieve better performance gains than the existing orthogonal multiple access (OMA)techniques [3, 4].

The concept of power domain NOMA is like superposition coding. The transmit information signal of the user equipments (UEs),connected to the same base station (BS), is superposed using power domain, by non-orthogonally multiplexing it over one transmit signal. In easy words, at the transmitter the non-orthogonal part allows this technique to overlap the signal information of multiple UEs, connected to the same BS, in one transmit signal. At the receiver side, the UEs use power domain to separate their own downlink signal from the superposed one [4]. To successfully implement the NOMA concept, it requires some advanced reception technique to separate the superposed signal information at the UE, such as successive interference cancellation (SIC). SIC enables a UE to separate its own required signal information from the superposed transmitted signal by canceling out the unwanted signal components [5]. For using SIC with NOMA, it is important to know that which UE should perform the SIC. The decision is made by the order of increasing channel gain [4, 6]. The user that has high channel gain, referred to as cell center user (CCU),performs the SIC to decode superposed information of the low gain user, referred to as cell edge user (CEU). As NOMA utilizes power domain in order to superimpose signals of multiple UEs in a single transmitted signal,this creates a lot of interference at the receiver side. Although this interference is suppressed by SIC, but to further enhance the receiver performance, in this work, we have presented a joint Walsh-Hadamard transform (WHT)and NOMA approach for achieving better performance gains compared to the conventional NOMA. WHT increases the constellation diversity of the used modulation scheme, hence,resulting in reduced bit error rate (BER) at the UE receiver. The general concept of NOMA with WHT is shown in figure 1.

In this paper, a novel scheme for improving the receiver performance of NOMA is presented.

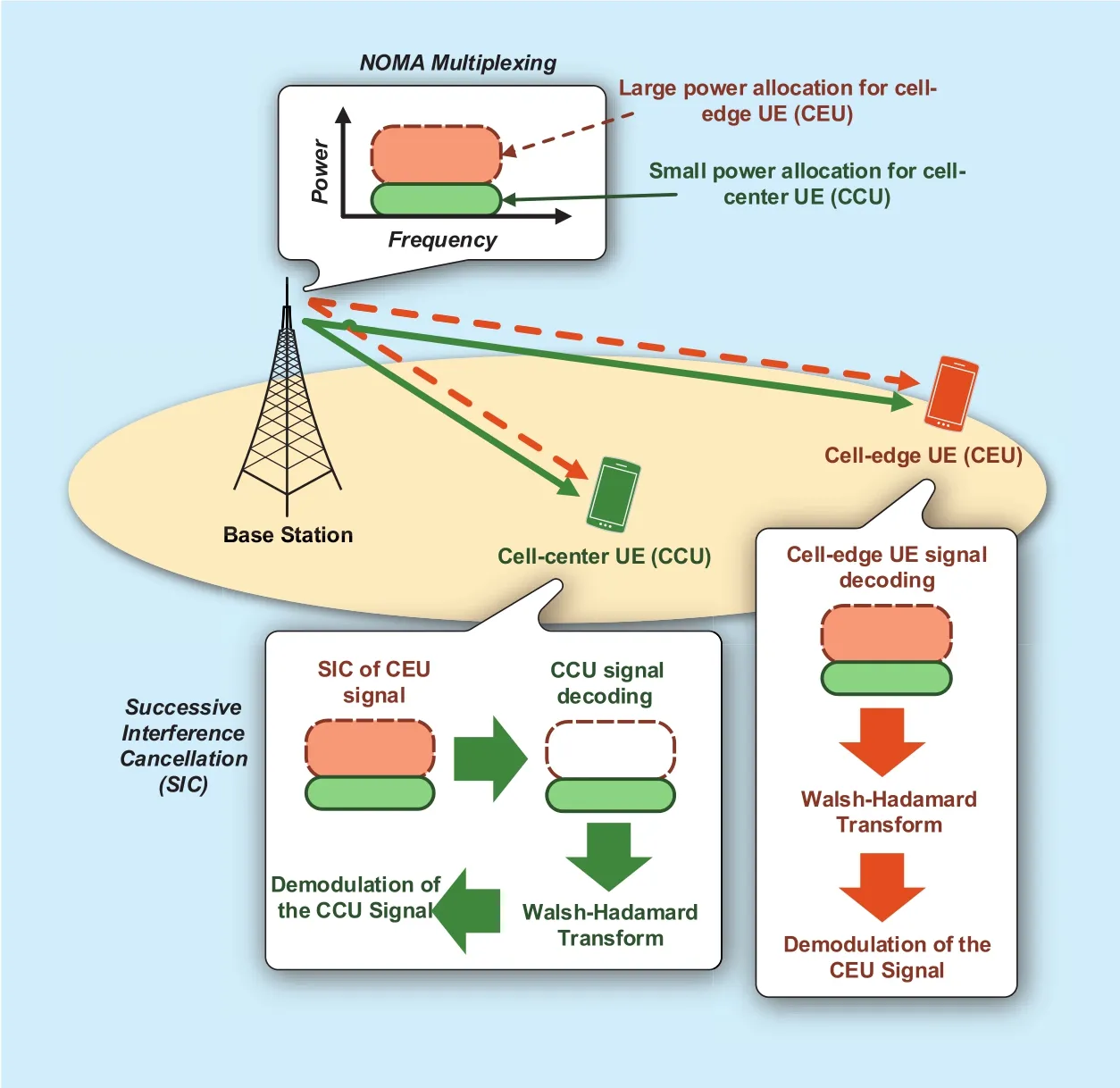
Fig. 1. The WHT-NOMA concept.

To date, a lot of research has been conducted on NOMA with SIC to reduce the BER and enhance the system performance and throughput. The significance of NOMA with SIC is well explained in [3], starting with cellular multiple access to the evolution of FRA. In[4], the importance of SIC-NOMA with an extension of BS antenna beam sectorization concept is detailed. Similarly, the authors in[5] and [7], investigated system-level and link-level performance respectively using SIC-NOMA in the cellular downlink. In [8],the application and importance of NOMA in LTE and 5G networks was elaborated. Similar study was conducted in [9]. The authors of [10], investigated the application of multi input multi output NOMA (MIMO-NOMA) in internet of things (IoT). Similarly, a design of massive MIMO-NOMA was proposed in [11],for limited feedback. Most of the research conducted so far provides new ideas to be implemented on SIC-NOMA for reducing the BER hence leading to better throughput performance. Similarly, we have also proposed a new approach in this work to be applied on SIC-NOMA for achieving better performance gain in terms of BER, peak to average power ratio (PAPR), user throughput and spectral efficiency. The proposed approach in this paper uses WHT together with the SIC-NOMA,referred to as WHT-NOMA. Furthermore,the approach is analyzed for both ideal and non-ideal SIC conditions in NOMA, explained in the later section of this work.

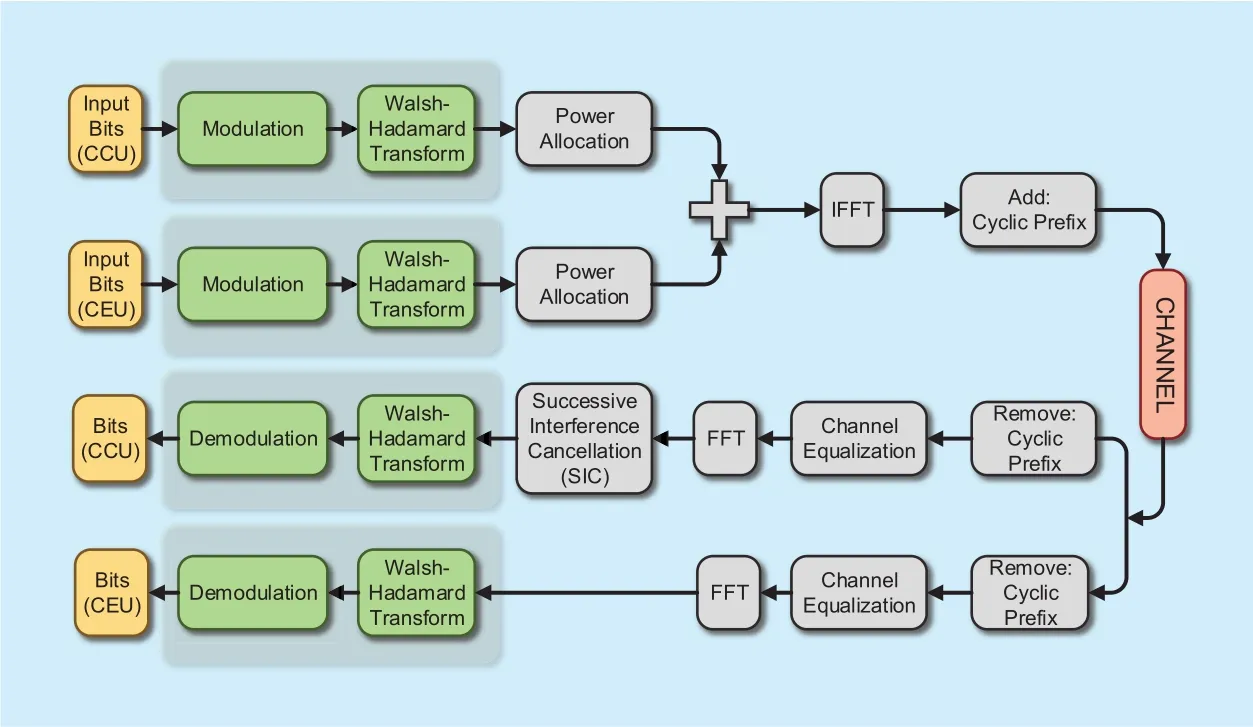
Fig. 2. The WHT-NOMA transceiver.

WHT is a well-known code used in communication systems [12]. It is used as orthogonal variable spreading factor (OVSF)in communication systems like code division multiple access (CDMA) and universal mobile telecommunications system (UMTS). Applying WHT to the transmit symbols of a modulation scheme, merges two or more symbols,dependent upon the order of WHT matrix, into one symbol. This results in constellation diversity, achieving high performance gains. Such work was performed in [13] for wireless communication networks using WHT with Alamouti scheme for reducing BER of the system.Authors in [14], applied WHT on IEEE 802.16 WiMAX system achieving high performance gains hence reducing the BER. In [15], WHT was combined with spatial modulation (SM)to achieve robustness against the wireless fading channels. A similar study was performed in [16], where the authors presented a combination of WHT and generalized frequency division multiplexing (GFDM) for reducing BER in wireless networks. To the authors best knowledge, application of WHT to downlink NOMA has never been investigated before and this work is the first to investigate BER,PAPR, spectral efficiency and user throughput performance using the joint WHT and NOMA approach. Although the main contributions have been mentioned before but they are summarized as follows:

• Application of WHT to power domain NOMA results in increased constellation diversity achieving higher performance gains than the conventional NOMA system.

• The proposed WHT-NOMA shows significant reduction in the PAPR and BER achieving better user throughput performance compared to the conventional NOMA. The claim is justified by performing MATLAB simulation in the last section of this paper.

Rest of the paper is organized as follows;Section II contains system model with details of proposed WHT-NOMA scheme along with throughput and PAPR description, Section III contains simulation results of the proposed WHT-NOMA, followed by the conclusion and future work in Section IV.

II. THE PROPOSED MODEL

This section starts with the detailed description of the basic NOMA model and the WHT technique. Following this, the system model of the proposed WHT-NOMA is provided with the analysis in ideal and non-ideal SIC conditions.Then the section ends with the throughput and PAPR analysis in WHT-NOMA. The block diagram of proposed WHT-NOMA transceiver is given in the figure 2.

2.1 Non-orthogonal multiple access(NOMA)

This part provides the description of basic NOMA model. Let’s suppose that a base station (BS) transmits a superposition coded signal S for k paired UEs given as:

where, k ∈{1,2,3,…,N }, skis the signal of kthUE and Pkis the total transmission power for the k paired UEs. According to the existing literature of NOMA, the maximum number of users in a pair is not yet standardized. As mentioned earlier in Section I, in user pairing there are two kinds of UEs, i.e., high gain CCUs and low gain CEUs. The ascending value of index k is assigned in the descending order of the UE channel gain, i.e., k=1 is the highest gain user, categorized as CCU, and k=N is the lowest gain user, categorized as CEU. The received superposition coded signal at the kthUE is given as:

Using (1) and (2) gives:

where, hkgives response of the transmission channel from BS to the kthUE, which in this work is considered as the Rayleigh fading channel and n represents noise, which in this case is considered as additive white Gaussian noise (AWGN) with zero mean and variance.Here Pkis the transmission power associated with the kthUE in the pair given as:

where, ∝kgives the ratio of power assignment to the kthUE, PBSrepresents the serving BS transmission power and no. of sub-bands in the system are given by NSB. In general, ∝kcan take any theoretical value [4].

Now as mentioned before, to extract the desired signal information from the received superposition coded signal of the k paired UEs, a UE-receiver must perform SIC. To do this correctly, it is very important that the UE receiver knows the optimum order of decoding within its paired UEs. This order is determined through the channel-gain of the k paired UEs in a way that only the high gain users (CCUs)perform SIC to remove the signal information of the low gain users (CEUs) as shown in figure 1. Let’s consider a high channel gain user m as CCU in k paired UEs. Then UE-m must perform SIC to extract its signal by removing the signal information of the low gain UEs within its pairing. The UE-m received signal is given as:

To simplify the problem and as per the existing literature for NOMA receiver, let’s consider a two-user case. So, for two UE case, the received signal at UE-1 is given by using (5)as:

where, s1, P1and h1are the signal-information, power, and channel-response respectively of the high gain user UE-1, and s2and P2are signal information and power respectively of the low gain user UE-2. For further investigation of the received signal at the receiver, two cases are considered, i.e., NOMA with ideal and non-ideal SIC.

1) NOMA Receiver with Ideal SIC

In this case, it is assumed that the CCUs have perfect knowledge of the CEUs signal information and the channel effects are not considered. This means that signal information of CEUs is perfectly cancelled at CCUs by performing SIC. If the CCU is UE-m in the k paired UEs, then it’s received signal, by performing ideal SIC, is given by using (5):

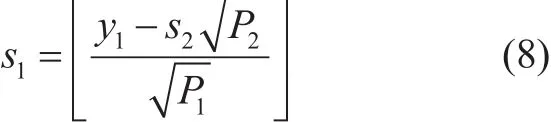
2) NOMA Receiver with Non-ideal SIC

In this case, the NOMA receiver performance is investigated in a non-ideal condition.The case is considered because it is more inclined towards a somewhat practical behavior.Here, the CCU performs SIC in presence of the channel effects produced by the transmission channel, which in our case is Rayleigh fading channel, hence creating a more practical approach than the ideal SIC case. Now let’s suppose that, in the k paired UEs, for the received signal at UE-m in (5), the signal information of the CEUs with non-ideal condition is given as:

where, n represents the AWGN and hkis the Rayleigh fading channel. Then the signal extraction of UE-m after performing SIC is given by using (9):

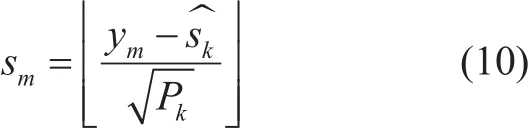
For the case of two paired UEs, the CEU is UE-2 and CCU is UE-1. So, in the received signal at UE-1, the signal information of UE-2, after including the effects of Rayleigh fading channel, is given by (9):

The extracted signal of UE-1 after performing SIC is given as:

After the description of NOMA receiver with the ideal and non-ideal SIC cases we move towards the WHT part.

2.2 Walsh-hadamard transform(WHT)

This part provides the basic WHT model, that is later used for the proposed WHT-NOMA.As explained in Section I, WHT is used as an OVSF in the communication systems, so, to achieve the constellation diversity, WHT is applied to the transmit symbols of the used modulation scheme. The transform is achieved by multiplying WHT matrix with input signal at the transmitter side. Similarly, the signal is recovered at the receiver side by multiplying same WHT matrix with the received signal.The input-output expression is given as:

where, S and y are the input and output signals respectively and Hiis the WHT matrix with i=2llength code (l∈ℤ+). In the WHT matrix, every two different rows represent two perpendicular vectors meaning that it has mutually orthogonal rows. To illustrate the WHT matrix, let’s suppose that if H is a Hadamard matrix then the partitioned matrix is given as:

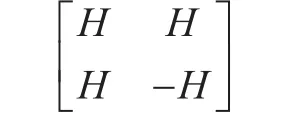
this observation gives the general sequence of WHT matrix as:

where, the normalization factor is given asand j represents the order of Hadamard matrix to derive the WHT matrix Hi. Let’s suppose that the complex constellation points of the modulator-output data (such as quadrature amplitude modulation (QAM) or phase shift keying (PSK)) are given as: xdata=[x1x2x3… xn]then the resultant, after WHT matrix application, is given as:

where, SHis reconstruct-able using (13). To have easy and better understanding of the process, let’s assume that the given data is xdata=[x1x2] with the WHT matrix of order 2, i.e., H2. So, then by using (14), Eq. (15) is written as:

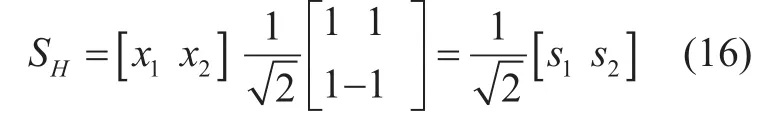
which yields:

The derived resultant points in (17) and(18) are then transmitted instead of the original data. If we consider a typical QPSK transmitter, then the modulator yields four complex constellation points, i.e., 00, 01, 10, and 11(example). The WHT application on these points is shown in table I, where xˆ1and xˆ2are complex constellation points of their respective x1and x2modulation points. The new constellation points after the WHT application are represented by s1and s2.

At the receiver side, for inverse WHT, the Hadamard matrix of the same order is applied to the received data. The inverse WHT process is given as:

The resulting Eq. (19) shows the diversity achieved by using the WHT technique.

After the description of WHT application for achieving the constellation diversity, next section provides the proposed NOMA with WHT.

2.3 Proposed WHT-NOMA

This part provides the description of the proposed NOMA with WHT technique. The block-diagram of the proposed technique is provided in figure 2. If superposition coded signal at the transmitter is given by (1), then after WHT application the transmit signal is given as:

where, sH,krepresents the signal of the kthUE after the WHT is applied. Similarly, at the receiver side using (3) the received signal at the kthuser is given as:

where, hkis the channel response, considered as Rayleigh fading channel and n represents noise, considered in this work as AWGN with zero mean and variance.

In WHT-NOMA, for the mthuser case in k paired UEs, the received signal of high gain user UE-m in (5) without performing SIC can be written as:

Similarly, for the two UE case in WHT-NOMA, the received signal at UE-1 without SIC will be given by using (22):

Here also, just like conventional NOMA in subsection A of this Section, two cases are considered for SIC at the receiver, i.e.,WHT-NOMA with ideal and non-ideal SIC.

1) WHT-NOMA Receiver with Ideal SIC

Just like the conventional NOMA receiverin subsection A of this section, it is assumed that the CCUs has perfect knowledge of the signal information of CEUs. The CCUs cancel the signal information of the CEUs completely from the combined signal using SIC. Then in WHT-NOMA receiver, the signal of high gain user UE-m, in the k paired UEs, is retrieved using (23):

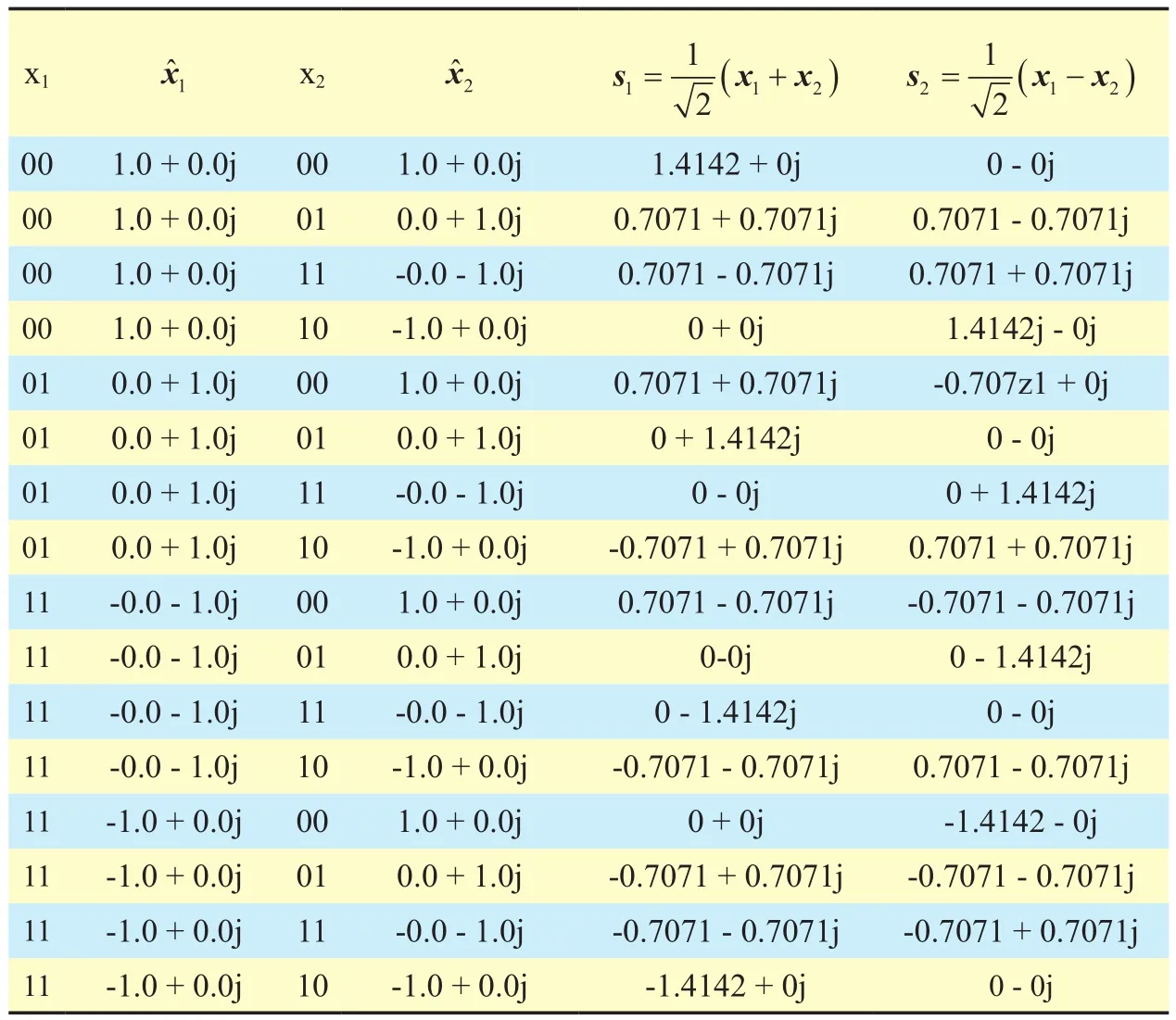
Table I. New constellation points after application of WHT.

where, Hiis the WHT matrix of the same order i as used for the transmitter anddenotes the demodulation and detection of the received signal. In the two paired UEs case, to retrieve the signal of high gain user UE-1, (24)is written as:

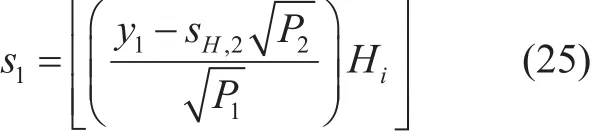
2) WHT-NOMA Receiver with Non-ideal SIC

In this case, just like the conventional NOMA receiver in subsection A of this section, CCUs perform SIC in the presence of channel effects produced by the transmission channel, i.e., in our case Rayleigh fading channel. Here, for WHT-NOMA, the signal information of CEUs at the UE-m is given by using (22):

where, n and hkrepresent AWGN and the Rayleigh fading channel respectively. The signal information of UE-m is extracted using(22) and (26) as:

For the two paired UEs case in WHT-NOMA, the signal information of UE-2 at UE-1,after including the effects of Rayleigh fading channel, is given using (26):

The UE-1 signal can be extracted using(23) and (28) as:

where, as aforementioned, Hiis the WHT matrix of the same order i as used for the transmitter andrepresents the demodulation and detection of the received signal.

After the description of WHT-NOMA receiver for both ideal and non-ideal SIC cases,next is the throughput performance for the proposed WHT-NOMA.

2.4 WHT-NOMA: throughput performance

In this section, we briefly discuss about the throughput calculation of conventional NOMA and the proposed WHT-NOMA. As explained in [17], throughput and BER are related to each other, thus, the throughput can be calculated using BER. So, in this work,for both cases, i.e., conventional NOMA and WHT-NOMA, throughput calculation is based on the BER performance given as [17]:

where, B is the bandwidth and Q is the modulation order of the transmitted signal.

The next section gives the details of PAPR in proposed WHT-NOMA.

2.5 WHT-NOMA: peak to average power ratio (PAPR)

This part presents the PAPR description for the proposed WHT-NOMA technique. In this work, NOMA is employed with orthogonal frequency division multiplexing (OFDM) as the signal waveform, same as LTE baseline[3, 7]. Use of OFDM induces high PAPR, one of the main drawbacks of multicarrier modulation (MCM) systems [18]. Such high PAPR makes high power amplifier (HPA) to operate in non-linear region and thus, lowers the energy efficiency of the system [19]. Therefore,PAPR reduction is a good measure to analyze the performance of any MCM system. For this reason, in this section, PAPR performance of the proposed WHT-NOMA is discussed.

The ratio of peak power to average power of the superimposed signal S in (20), after the

WHT application, is expressed as [20]:

where, E{.} represents expectation of the transmitted signal. Further, PAPR of the transmitted signal S is bounded by [21]:

where, L is the number of sub-carriers and γ is defined as:

where, ρSis the autocorrelation among the symbols. Therefore, low autocorrelation results in low PAPR value.

The idea behind application of the WHT in NOMA system is to reduce the autocorrelation of the input signal so that the amplitude of the resultant signal may not magnify after inverse fast Fourier transform (IFFT) operation. Implementation of WHT in NOMA spreads the energy of the superimposed signal either in the whole spectrum or some parts of the spectrum[22]. This spreading lowers the amplitude of the overlapped samples and thus, lowers the autocorrelation among samples, hence, resulting in reduced PAPR value.

In (31), the instantaneous mean power,, and the maximum power of the signal S are given respectively as [23]:

Thus, the overall PAPR of the precoded signal S in (20) can be expressed by using (34),(35) and (31) resulting as:

The PAPR of the transmitted signal S is also varied depending on the constellation size. Thus, the PAPR of signal modulated with QAM is given as [23]:

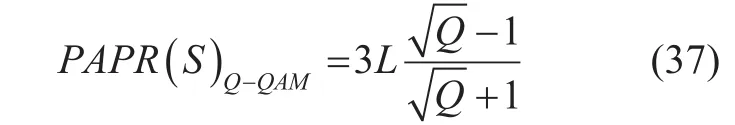
where, Q is the constellation size of the modulated signal for the k th user. Similarly, if the signal is phase modulated then PAPR is given as [23]:

PAPR is considered a random variable as its value is dependent on the OFDM signal which is random in nature. Therefore, properties of PAPR are best described using complementary cumulative distribution function (CCDF). The CCDF of the precoded signal S in (20) can be approximated from [24] as:

where, Pavgis the average power of the signal.

To date, different techniques have been proposed to reduce the PAPR, however in this work, application of WHT lowers the PAPR by minimizing the autocorrelation among samples as shown in Fig 3. The figure shows normalized autocorrelation function(ACF) among sequences from conventional NOMA and proposed NOMA system. It can be observed that the autocorrelation among sequences from conventional NOMA has high values which leads to high PAPR values. On the other hand, the proposed WHT-NOMA system breaks the autocorrelation and manages to reduce it, thus, resulting in low PAPR.Therefore, use of WHT with NOMA tends to increase the PAPR reduction gain which is further detailed in subsection C of Section III.

Fig. 3. Comparison of the normalized autocorrelation function (ACF) using conventional NOMA and WHT-NOMA.

Next section provides the simulated resultsof the proposed WHT-NOMA compared with the conventional NOMA.

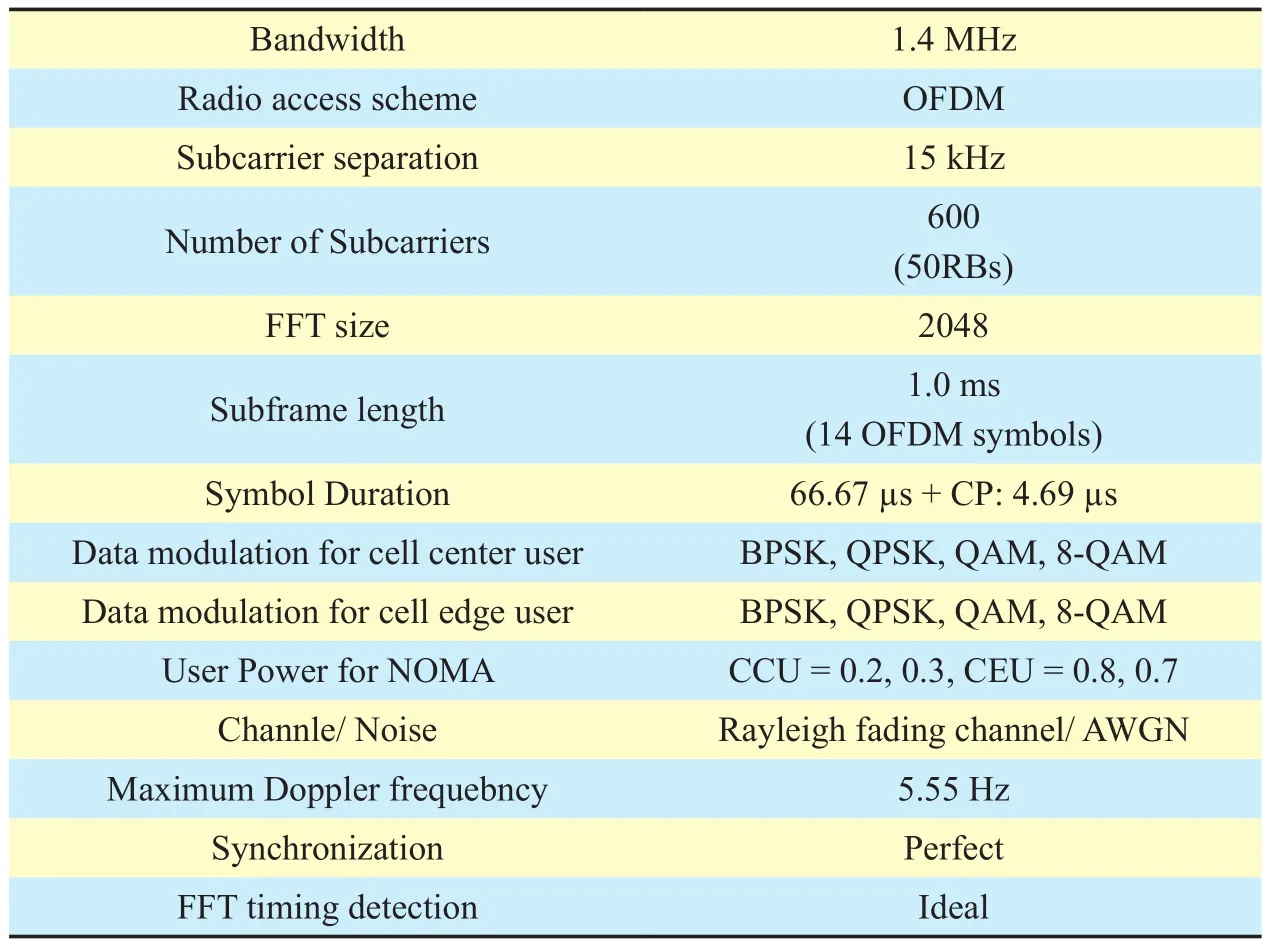
Table II. Simulation parameters.

Fig. 4. BER performance for downlink NOMA and WHT-NOMA using BPSK modulation and power allocation: CCU = 0.2 and CEU = 0.8.

III. SIMULATION RESULTS

This section provides simulation results for the proposed WHT-NOMA in comparison with the conventional NOMA scheme using ideal and non-ideal SIC conditions. The results are discussed in terms of BER, user throughput,PAPR, spectral efficiency and computational complexity. As NOMA has not been standardized yet, so the simulation parameters in this work follow the long-term evolution (LTE)standard as stated in the Third-Generation Partnership Project (3GPP) specifications. For the same reason, the basic signal waveform used for the simulations is also taken from the LTE standard. The simulation parameters are defined in table II. As the work concentrates on providing bene fits of WHT-NOMA so, any power allocation scheme could be used, here,for simplicity, we have used fixed power allocation for both CCU and CEU in the simulations, i.e., CCU = 0.2, 0.3 and CEU = 0.8, 0.7 respectively, where the total power is equal to 1, i.e., PCCU+ PCEU=1. For the WHT matrix order, we have used the same order as for the used modulation scheme, e.g., for BPSK modulation, the order of WHT matrix is 2 and for QPSK modulation, the order of WHT matrix is 4. As synchronization between different nodes in multi-user system is another crucial factor to improve the diversity of the system [25];however, in this article perfect synchronization is assumed to solely highlight the impact of WHT on NOMA. The results are given as follows:

3.1 WHT-NOMA: BER

This part shows the BER performance of WHT-NOMA compared with conventional NOMA, under the ideal and non-ideal SIC conditions using different modulation schemes.The results are provided in Figs. 4 to 9.

Fig. 5. BER performance for downlink NOMA and WHT-NOMA using QPSK modulation and power allocation: CCU = 0.2 and CEU =0.8.

Fig. 6. BER performance for downlink NOMA and WHT-NOMA using QAM modulation and power allocation: CCU = 0.2 and CEU =0.8.

Fig. 7. BER performance for downlink NOMA and WHT-NOMA using 8-QAM modulation and power allocation: CCU = 0.2 and CEU= 0.8.

Fig. 8. BER performance for downlink NOMA and WHT-NOMA using QPSK modulation and different power allocations for CCU and CEU.

In figure 4, the results are shown for conventional NOMA and WHT-NOMA using binary phase shift keying (BPSK) modulation. It can be observed for WHT-NOMA that there is a performance gain of almost 5～10dB in SNR for different BER values in both ideal and non-ideal SIC conditions. The receiver performance of WHT-NOMA is better than conventional NOMA for both ideal and non-ideal SIC cases. As CCU is the high gain user so it is assigned low power as compared to CEU. The performance of CEU is better than CCU as SIC is performed only by CCU. Similar trend can be seen in figure 5 where quadrature phase shift keying (QPSK) modulation is used with WHT matrix of order 4 (H4from (14)).

Fig. 9. BER performance for downlink NOMA and WHT-NOMA using 8-QAM modulation and different power allocations for CCU and CEU.

For higher order modulation schemes, we have used quadrature amplitude modulation(QAM) and 8-QAM in our simulation results.It can be observed that in Figs. 6 and 7, the trend in performance gains for WHT-NOMA is similar to the results in Figs. 4 and 5. In figure 7, BER value for conventional NOMA,with ideal SIC, at 15dB SNR is closer to 100,which is highly undesirable, whereas, for WHT-NOMA, BER is between 10-1to 10-2at 15dB SNR. Here also, the performance gain of WHT-NOMA stays the same for both ideal and non-ideal SIC conditions, i.e. 5～10dB.This shows that there is a significant receiver performance gain in the terms of BER for WHT-NOMA compared with the conventional NOMA.

To have further insight on the trend of BER performance, the results with different power allocations for CCU and CEU, i.e., CCU = 0.3,0.2 and CEU = 0.7, 0.8, are provided in Figs.8 and 9 using QPSK and 8-QAM respectively.It can be observed that by increasing the power of CCU and decreasing CEU’s power, the BER performance of CCU improves with little degradation in BER performance of CEU.

Further, we move towards our throughput results calculated by using the above BER performance.

3.2 WHT-NOMA: Throughput

This part of the paper provides the throughput performance of WHT-NOMA compared with the conventional NOMA under both ideal and non-ideal SIC conditions. The results are based on the BER performance shown in subsection A of this section. The results are provided in Figs 10 to 15.

In figure 10, the results are provided for BPSK modulation. It can be observed that WHT-NOMA provides better throughput performance than the conventional NOMA for both CCU and CEU in both ideal and non-ideal SIC cases. As an example, the results show that approximately 0.48Mbps increase in throughput performance of CCU can be achieved at 10dB SNR by using WHT with NOMA under the ideal SIC conditions.Similar trend is followed for the CCU with non-ideal SIC and CEU at 10dB SNR, achieving an increase of 0.32Mbps and 0.36Mbps in the throughput performance respectively.Similarly, the results shown in Fig 11. using WHT-NOMA with QPSK modulation follow the same trend, e.g., at 10dB SNR the increase in throughput performance is as; 1.29Mbps for CCU with ideal SIC, 1.30Mbps for CCU with non-ideal SIC and 0.96Mbps for CEU.

The results shown in Figs 12 and 13 are obtained using higher modulation schemes,i.e., QAM and 8-QAM. It can be observed that using WHT-NOMA with higher modulations,also show significant increase in the throughput performance of the users. For example, in Fig 13, for 8-QAM at 10dB SNR, the increase in throughput performance is as; 2.05Mbps for CCU with ideal SIC, 1.98Mbps for CCU with non-ideal SIC and 2.07Mbps for the CEU.

Like the BER performance, to understand the trend of throughput performance, the results with different power allocations for CCU and CEU, i.e., CCU = 0.3, 0.2 and CEU= 0.7, 0.8, are provided in Figs. 14 and 15 using QPSK and QAM respectively. It can be observed that increasing the power of CCU and decreasing CEU’s power, the throughput performance of CCU improves with little deg-radation in throughput performance of CEU.

Fig. 10. Throughput performance for downlink NOMA and WHT-NOMA using BPSK modulation and power allocation: CCU =0.2 and CEU = 0.8.

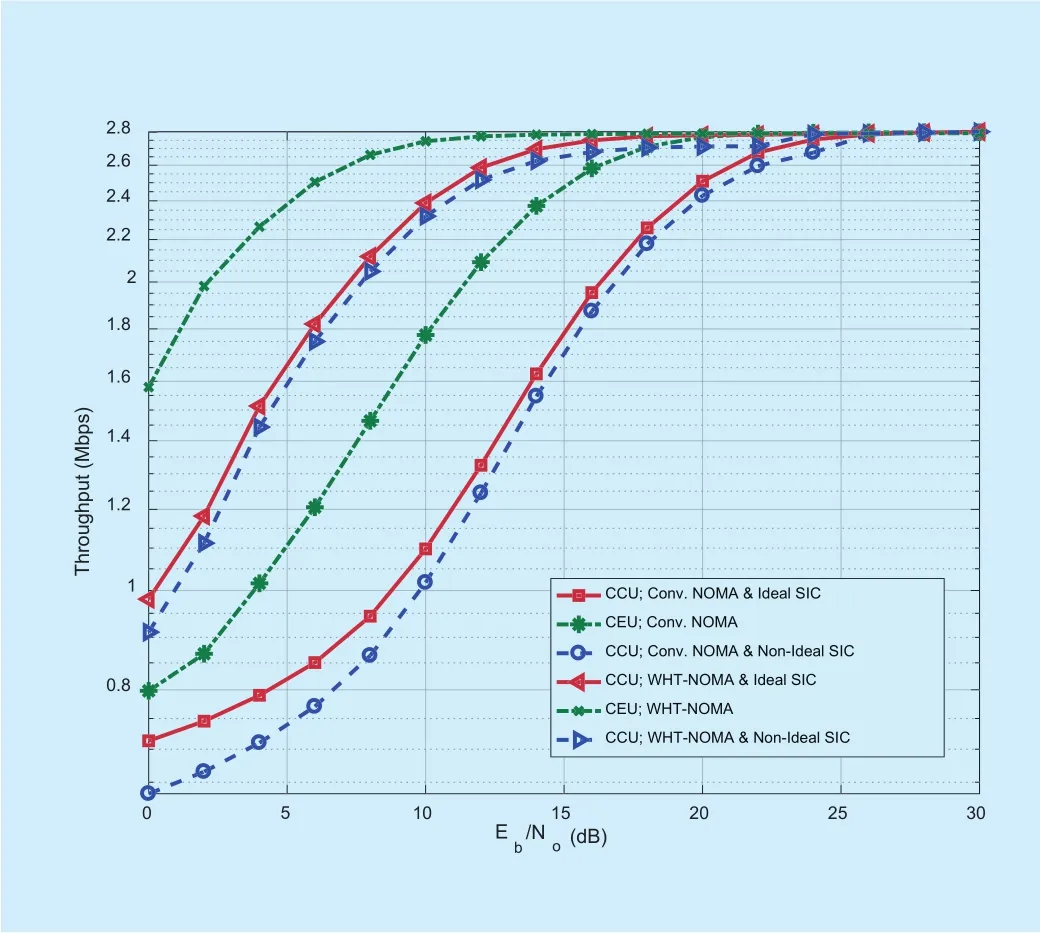
Fig. 11. Throughput performance for downlink NOMA and WHT-NOMA using QPSK modulation and power allocation: CCU =0.2 and CEU = 0.8.

Fig. 12. Throughput performance for downlink NOMA and WHT-NOMA using QAM modulation and power allocation: CCU =0.2 and CEU = 0.8.

Fig. 13. Throughput performance for downlink NOMA and WHT-NOMA using 8-QAM modulation and power allocation: CCU= 0.2 and CEU = 0.8.

Next, we provide the PAPR performance results using WHT with NOMA.

3.3 WHT-NOMA: PAPR

In this section, we have analysed the performance of proposed NOMA-WHT compared to conventional NOMA in terms of PAPR reduction gain. The simulations are carried out with both users using same modulation technique irrespective of their channel gains and with both users having different modulation technique depending on their channel gains.

Fig. 14. Throughput performance for downlink NOMA and WHT-NOMA using QPSK modulation and different power allocations for CCU and CEU.

Fig. 15. Throughput performance for downlink NOMA and WHT-NOMA using 8-QAM modulation and different power allocations for CCU and CEU.

Figure 16 presents the CCDF comparison of conventional NOMA and NOMA-WHT when both CCU and CEU are transmitting on same modulation technique, i.e., BPSK, selected because of its simplicity. It can be noticed that at a CCDF of 10−3, conventional NOMA with number of sub-carriers, L = 64 has PAPR equal to 11.2dB, whereas, WHT-NOMA for L = 64 at a CCDF of 10−3has PAPR equal to 8.9dB. It shows our proposed system achieves a PAPR reduction gain of 2.3dB. This result is supported from figure 3 where ACF for WHT-NOMA is lower than the conventional NOMA. Another comparison can also be drawn from this figure that when the number of sub-carriers are increasing, PAPR reduction gain is getting low. WHT-NOMA with L = 64,16 and 4 are also simulated in figure 16.

The trend of PAPR reduction for WHT-NOMA with the number of sub-carriers demonstrates that increment in sub-carriers leads to high PAPR.

Another comparison related to PAPR reduction, as displayed in figure 17, is for the scenario where adaptive modulation is simulated. Here CCU with high channel gain employs 8-QAM whereas CEU with low channel gain operates at QPSK. It is shown that at a

CCDF 10−3, PAPR value for conventional NOMA with L = 64 is 12.8dB whereas for WHT-NOMA its value is 10dB. It means that with proposed approach, the system achieves a PAPR reduction gain of 2.8dB. However,this gain can be increased by decreasing the number of sub-carriers as demonstrated in figure 17, where WHT-NOMA with L = 16 and 4 is achieving gain of 0.5dB and 3.3dB over WHT-NOMA with L = 64. This trend validates the findings in the literature [26] and[27]. Although, in this paper classical OFDM is employed; however different evolutional multicarrier variants of OFDM have been adopted in literature [28, 29] to analyse the performance of multicarrier systems. Investigations on the performance of these OFDM variants with NOMA based systems opens a new direction of research to evaluate the PAPR performance of the system.

3.4 WHT-NOMA: spectral efficiency

This section presents the comparison of WHT-NOMA with classical NOMA on the basis of spectral efficiency. The Signal to noise distortion ratio (SNDR) for NOMA system can be expressed as [30]:

Fig. 16. Comparison of PAPR reduction performance of conventional NOMA and WHT-NOMA with CCU and CEU = BPSK modulation. Power allocation: CCU = 0.2 and CEU = 0.8.

Fig. 17. Comparison of PAPR reduction performance of conventional NOMA and WHT-NOMA with adaptive modulation (CCU =8-QAM, CEU = QPSK). Power allocation: CCU = 0.2 and CEU =0.8.

where, Psand Pnrepresent signal and noise power respectively, and PDis the distortion caused by HPA. Therefore, the data rates for CCU and CEU, in NOMA system, in the presence of AWGN and HPA non-linear distortion,such that CCU is able to detect the CEU, can be defined as:

where, RCCUand RCEUare the data rates for CCU (UE-1) and CEU (UE-2) respectively.The ergodic sum rate Rsumof the NOMA system can therefore, be written as:

The results in figure 18 show the spectral efficiency of the CCU and CEU for conventional and proposed NOMA system in the presence of noise and distortion. Spectral efficiency for CCU in conventional NOMA system, at SNDR of 25dB, is 3.379 bps/Hz whereas for WHT-NOMA, its value is 3.678 bps/Hz. Thus, WHT-NOMA achieves almost 0.3 bps/Hz improvement in spectral efficiency for CCU as compared to conventional NOMA.Similarly, for CEU, the gain in terms of spectral efficiency reaches up to 0.06 bps/Hz.Figure 19 exhibits the ergodic sum rate of the system for conventional and WHT-NOMA in the presence of AWGN and amplifier distortion. WHT-NOMA outperforms conventional NOMA with a gain of 0.36 bps/Hz when SNDR is equal to 25dB. The increment in spectral efficiency for WHT-NOMA can be supported by the fact that presence of WHT introduces diversity in the system. Moreover,WHT also increases the resistance of system against non-linear distortion caused by HPA which follows a boost in spectral efficiency.

3.5 WHT-NOMA: computational complexity

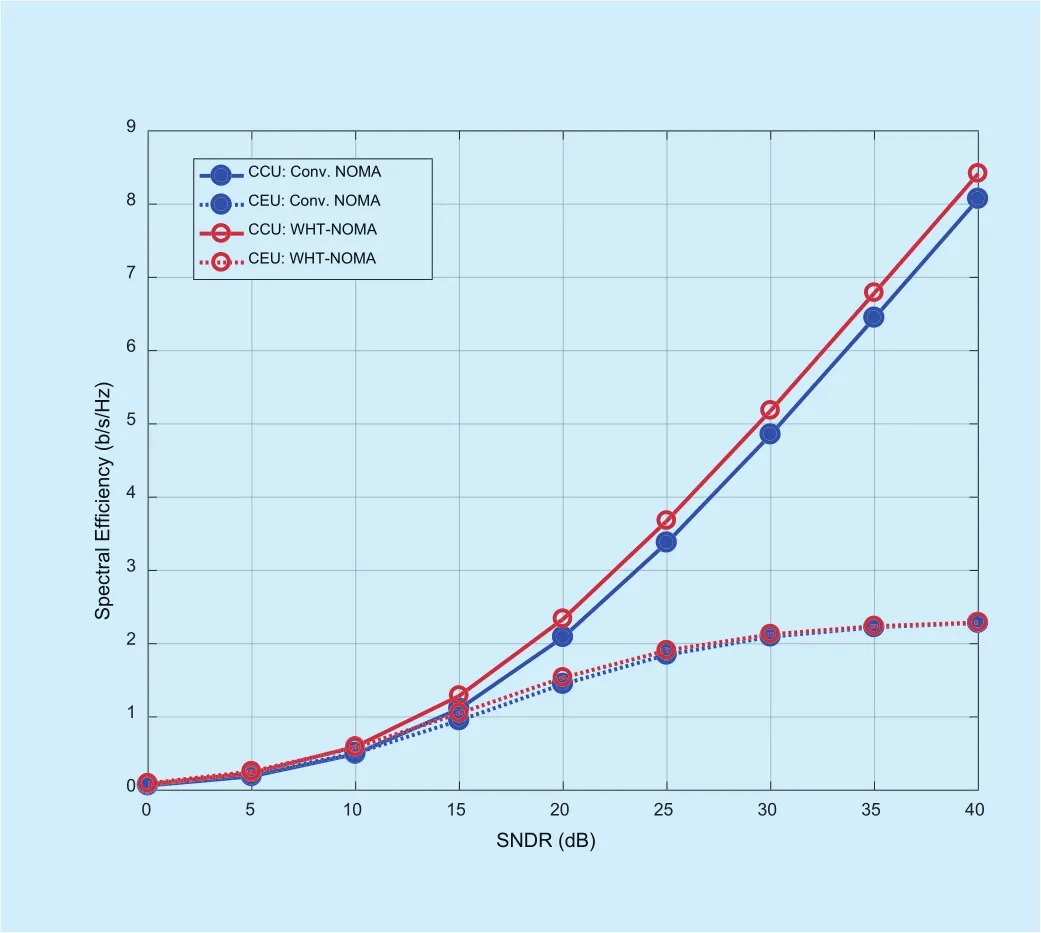
Fig. 18. Average rate achieved by CCU and CEU for conventional NOMA and WHT-NOMA in the presence of AWGN and HPA distortion, power allocation: CCU = 0.2 and CEU = 0.8.

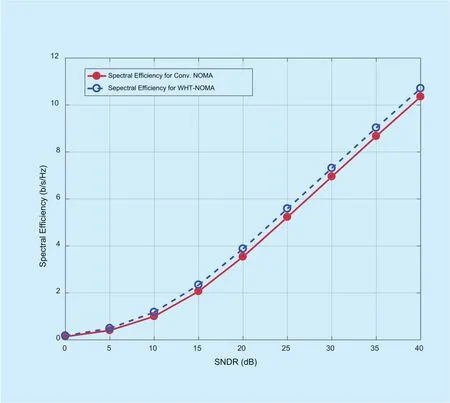
Fig. 19. Ergodic sum rate achieved by CCU and CEU for conventional NOMA and WHT-NOMA in the presence of AWGN and HPA distortion.

Computational complexity is another important performance metric to decide the feasibility of any proposed technique. This section analyses the computational complexity for classical NOMA and proposed WHT-NOMA.Both conventional and proposed NOMA systems require inverse discrete Fourier transform(IDFT) and discrete Fourier transform (DFT)at the transmitter and receiver sides respectively; however, an additional block of WHT is required for the proposed WHT-NOMA system. If L is the total number of sub-carriers in the system, then the number of complex multiplications and additions required at the transmitter (Tx) and receiver (Rx) for conventional NOMA and proposed WHT-NOMA system is shown in table III. In addition, the overall computational complexity for NOMAand WHT-NOMA in the form of number of complex operations as a function of number of subcarriers (L) is also exhibited in figure 20.It is evident from the figure that WHT-NOMA has high complexity as compared to conventional NOMA. Thus, the advantages of WHT-NOMA in the form of better BER, reduced PAPR, better throughput and improved spectral efficiency comes at the expense of slight increment in the computational complexity.

Table III. Computational complexity.

After the simulation results section, the concluding remarks are provided in the next section of this work.

IV. CONCLUSION

In this work, a novel scheme for improving the receiver performance of NOMA is presented. The proposed scheme WHT-NOMA provides better throughput and BER performance at low SNRs as compared to the conventional NOMA. As visible from the simulation analysis, it is shown that WHT-NOMA can improve the receiver performance gains up to a significant level. The WHT matrix works as a catalyst for the conventional NOMA and improves the BER with a SNR gain of up to 10dB. Further, PAPR reduction is also achieved using WHT-NOMA compared with the conventional NOMA which is also shown with the help of simulation results. Receiver design of NOMA needs careful consideration as multiple users are paired together in power domain and this creates a lot of interference at the receiver.The presented technique improves BER and throughput performance of the both high and low channel gain users.

The work is underway to include more interference cancellation techniques like iterative SIC and parallel interference cancellation(PIC) etc. The work will also be extended to multiuser case for checking the performance of WHT-NOMA in more complex environments. Further, the extension will analyze the performance of proposed method with various transmit and receive diversity techniques such as MIMO-NOMA.

Fig. 20. Number of complex operations for conventional NOMA and WHT-NOMA based systems.

ACKNOWLEDGEMENTS

This work was supported by Priority Research Centers Program through the National Research Foundation of Korea(NRF) funded by the Ministry of Education, Science and Technology (2018R1A6A1A03024003).