Asymptotic Analysis for Low-Resolution Massive MIMO Systems with MMSE Receiver

Kai Liu, Cheng Tao,＊, Liu Liu,2, Tao Zhou,2, Yinsheng Liu

1 Institute of Broadband Wireless Mobile Communications, School of Electronics and Information Engineering,Beijing Jiaotong University, Beijing 100044, China.

2 National Mobile Communications Research Laboratory, Southeast University, Nanjing 210096, China.

3 State Key Laboratory of Rail Traf fic Control and Safety, Beijing Jiaotong University, Beijing 100044, China.

Abstract: The uplink achievable rate of massive multiple-input-multiple-output (MIMO)systems, where the low-resolution analog-to-digital converters (ADCs) are assumed to equip at the base station (BS), is investigated in this paper. We assume that only imperfect channel station information is known at the BS. Then a new MMSE receiver is designed by taking not only the Gaussian noise,but also the channel estimation error and quantizer noise into account. By using the Stieltjes transform of random matrix, we further derive a tight asymptotic equivalent for the uplink achievable rate with proposed MMSE receiver.We present a detailed analysis for the number of BS antennas through the expression of the achievable rates and validate the results using numerical simulations. It is also shown that we can compensate the performance loss due to the low-resolution quantization by increasing the number of antennas at the BS.

Keywords: massive MIMO; low-resolution quantization; MMSE receiver.

I. INTRODUCTION

Massive multiple-input multiple-output(MIMO), as well-known as one of the key techniques for 5G wireless communication,has attracted a lot of research interest currently. The main idea of massive MIMO is to equip hundreds of antennas at the base station such that simple detection processing or transmit precoding can be employed in order to reduce the effect of noise and user interference, and hence, the spectral efficiency can be significantly improved [1]–[4].

During the process of the massive MIMO deployment, howerver, perhaps the most important issue that hinders its commercialization is the system power consumption and economic cost. On one hand, since massive MIMO systems have hundreds of BS antennas, the hardware cost might be unaffordable and prohibited if a dedicated radio frequency(RF) chain is equipped for each antennas. This motivates the use of hybrid precoding architectures in order to potentially reduce the hardware cost of the massive MIMO systems [5]–[8]. On the other hand, an alternative method to reduce the hardware cost is decreasing the resolution of the ADCs since the power consumption of the ADCs scales not only linearly with the bandwidth but also exponentially with the resolutions [9]–[12].

By considering the exact nonlinear property of a quantizer, the authors in [13] first evaluated the communication transmission limits imposed by low-resolution ADCs. However, it is dif ficult to deal with a nonlinear operation in general. Then in order to simplify the analysis,[14] proposed an additive quantization noise model (AQNM), which approximately reformulates the nonlinear quantizer as a linear one by treating the quantizer noise as additive and independent noise. By employing AQNM,there has been many work on the performance analysis for the low-resolution massive MIMO systems [15]–[23]. [16] investigated the effect of ADC resolution and bandwidth on the achievable rate for a multi-antenna system using the AQNM. [17] derived an approximation of the uplink achievable rate for low-resolution massive MIMO systems with maximum-ratio combining (MRC) receiver over Rayleigh fading channels. Then the result to the Rician fading channels has been extended in [18]. Then the authors in [19] investigated the performance of full-duplex relaying systems by employing the AQNM and derived the closed-form expression for the achievable sum rate with MRC/maximum-ratio transmission(MRT) processing. In order to reduce the performance loss of the low-resolution massive MIMO systems, [20] investigated the spectral efficiency performance of a mixed-ADCs massive MIMO system, in which low-resolution ADCs are equipped while few high-resolution ADCs are reserved. However, most of these prior work simply assumed that perfect channel state information (CSI) is known at the BS, which is not well justified in practical systems.

In this paper, the asymptotic uplink achievable rate for low-resolution massive MIMO systems is investigated. More precisely, we assume that imperfect CSI, which is acquired by pilot training, is known at the BS. Then,in contrast to prior work, we properly design the MMSE receiver that takes not only the AWGN but also the channel estimation error and quantization noise into account. Employing the proposed MMSE receiver, we then derive an asymptotic equivalent for the uplink achievable rate using the Stieltjes transform of random matrix. Finally, we present numerical results to verify our theoretical analysis.

In this paper, the uplink achievable rate performance of the low-resolution massive MIMO systems is investigated.

II. SYSTEM MODEL

In this section, a K single-antenna users and M BS-antenna massive MIMO system, where each antenna is assumed to be equipped with low-resolution ADCs, is considered. Since the uplink transmission is considered in this paper,we assume that the data transmitted from all K users to BS is independent, thus the analog signal received at the BS is

where G=HD1/2∈CM×Kis the channel matrix, n ～ CN (0, I )∈CM×1is the AWGN, and x∈CK×1is the data symbol vector, which satis fies the assumption of E{xxH} = I. More precisely, D∈ CK×Kis a diagonal matrix with the kth diagonal term dkbeing the largescale fading coefficient of the kth user, and H ∈CM×Kdenotes the small-scale fading channel matrix. In order to facilitate the representation, we vectorize the channel matrix G as= vect(G), and hence we have～ CN (0,Σg).

In this paper, the Rayleigh fading is assumed and hence, according to the definition of channel matrix G, we can readily obtain the covariance matrix Σgas

After the low-resolution ADCs, the quantized digital signal obtained can be represented as

where Z(.) is the quantizer function. As we can see from (3) that the quantized signal is complicated to deal with due to the nonlinear quantizer function. However, it is shown in[14] that if the gain of the automatic gain control is set appropriately and quantizer input is distributed as Gaussian, then the additive quantizer noise model (AQNM) can be employed to reformulate the quantized signal as

where κ=1−α and α is the inverse of the signal-to quantization-noise ratio [14].

More precisely, [17] listed the values of α for ADCs with 1-3 quantization bits.qu～ CN (0, Σqu)∈CM×1is the additive Gaussian quantizer noise that is independent with y.According to [17], the covariance matrix Σquof quantizer noise qufor individual channel realization is given by

It should be noted that the covariance matrix of the quantizer noise Σqudependents on the channel realizations.

III. CHANNEL ESTIMATION AND DATA TRANSMISSION

There has been limited prior work on the achievable rate analysis for the low-resolution massive MIMO systems with MRC/ZF receiver [17], [18], [21]. However, these prior work only assumed an ideal case that perfect CSI is known at the BS.

In contrast to these prior work, we assume that the CSI needs to be estimated at the BS by transmitting pilot sequences. Owing to the nonlinear quantization function, the channel estimation problem is challenging in low-resolution massive MIMO systems. Up to now,there has been many literatures working on this problem and different algorithms are proposed [12], [24]. Inspired by the recent work in [12], we will employ the LMMSE method to estimate the channels in the following.

3.1 Channel estimation stage

In the channel estimation stage, K users are assumed to transmit orthogonal pilot sequences to the BS simultaneously, i.e., FHF=τIK,where F∈Cτ×Krepresents the pilot matrix and τ is the length of the pilot. Then according to the AQNM, the quantized pilot signal matrix can be expressed as

where ppis the pilot transmit power,Np∈CM×τis the AWGN matrix. Qp∈CM×τis the quantizer noise in the channel estimate stage.

After vectorizing Zpas zp, we have

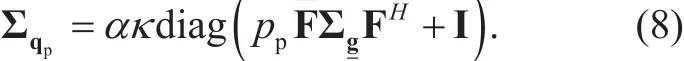
By following the standard reasoning of LMMSE method, then the LMMSE channel estimate can be given by

where

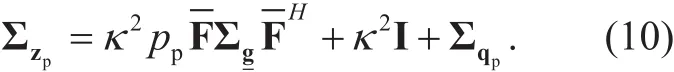
Considering (9), we can further obtain the covariance matrix ofg^ as

Inspired by [12], we consider a discrete Fourier transform (DFT) matrix as the pilot matrix in order to derive a concise expression of the covariance matrix. Therefore, by notingΣg= D ⊗I, we can obtain the covariance matrix Σqpof the quantizer noise qpas

Substituting (2) and (12) into (11) and employing the matrix inverse lemma, we can easily obtain

Similarly, the covariance matrix Σekof channel estimate errorcan be expressed as

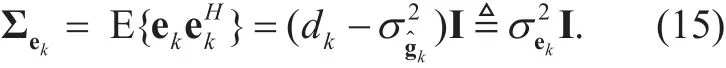
According to [25], we can see that the channel estimateis independent of the estimation error ekif the channel estimator in (9) is used. In addition, we denoteas the channel estimate matrix for all K users.

3.2 Uplink transmission stage

In the uplink transmission phase, we denote RHas the linear receiver. Then the quantized signal is processed as

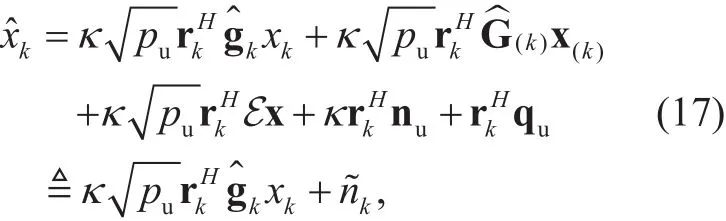
where rkis the kth column of R,iswith the kth column removed and so as well as x(k). We also refer the term n~kas the effective noise.

Since G^and E are independent for LMMSE channel estimation, the uplink SINR of the kth user is given by

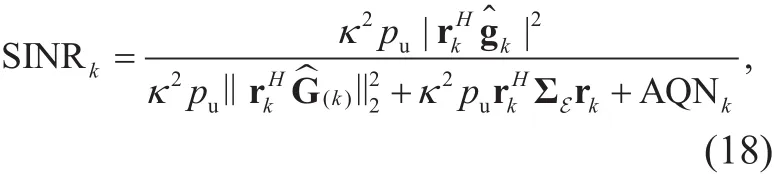
where

It is shown in [26] that for unquantized system, the MMSE channel estimator is the only estimator renders the additive channel estimation error uncorrelated with the data signals.For the quantized system considered in this paper, we can also readily obtain the correlation between the additive noise due to the estimation error and the data symbols based on the orthogonality property of MMSE as

This implies that in the low-resolution systems, the channel estimation error obtained by the LMMSE channel estimator (and hence the effective noise) are uncorrelated with the desired signal. Therefore, the achievable rate of the kth user can be given by

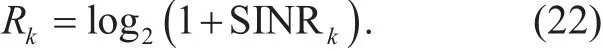
It should be noted that [22] is a lower bound, which is based on the fact that the additive Gaussian noise minimizes the mutual information between the input and output since the quantizer noise is treated as independent additive Gaussian noise for AQNM model.

IV. ASYMPTOTIC ACHIEVABLE RATE ANALYSIS WITH LMMSE RECEIVER

In this section, we will focus on deriving the achievable rate with MMSE receiver, which is properly designed by taking not only the AWGN noise, but also the channel estimation error and the quantizer noise into account,for low-resolution massive MIMO system.We also assume that both the number of users K and BS antennas M approach infinity with their ratio ξ= K/ M → ∞ is bounded.As can be seen later, the Stieltjes transform of the large dimension channel matrix G is employed in order to obtain the asymptotic achievable rate.

According to [25], the MMSE receiver of the kth user for a given channel estimate G^can be expressed as

where

It should be noted that, in contrast to the typical MMSE receivers, the receiver in (23)takes not only the AWGN but also the channel estimation error and the quantization noise into account. As we will see later, this improves the system performance.

In order to derive an asymptotic equivalent expression of Rk, we first provide an approximation of the covariance matrix Σqu. Based on the AQNM model, we note that the covariance matrix Σquis a diagonal matrix, which depends on the individual channel realization.For massive MIMO systems with K→∞, we can approximate Σquas

This is due to the approximation thatwhen K→∞. Thus, in the massive MIMO con figuration, the MMSE receiver in (23) for the kth user can be approximated as

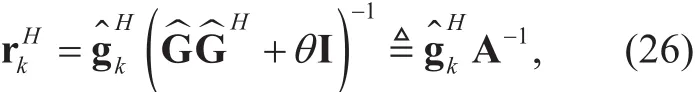
Accordingly, the kth user’s achievable rate in [22] can be approximated by

With the approximation above, we can obtain the asymptotic equivalent of Rkshown in Theorem 1.

Theorem 1: If the LMMSE channel estimator in (9) and the proper designed MMSE receiver in (23) are used in the low-resolution massive MIMO systems, then the asymptotic equivalent for the kth user’s achievable rate can be expressed as (28) shown below, where ψ and λ can be calculated as (38) and (40),respectively.

Proof: We first focus on deriving the asymptotic equivalent of the desired signal term. By observing thatand applying matrix inverse lemma, we have

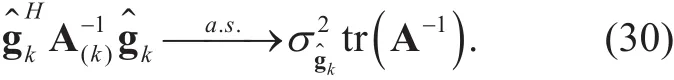
Thus the asymptotic equivalent of the desired signal power is given by

Then we deal with the asymptotic equivalent of the user interference term. In order to eliminate the dependence betweenand A, we rewrite

According to Lemma 7 in [27], we can obtain the asymptotic equivalent ofas

where the second step in (34) is based on the rank-1 perturbation lemma. Therefore, combining with (29) we can further obtain the asymptotic equivalent ofas

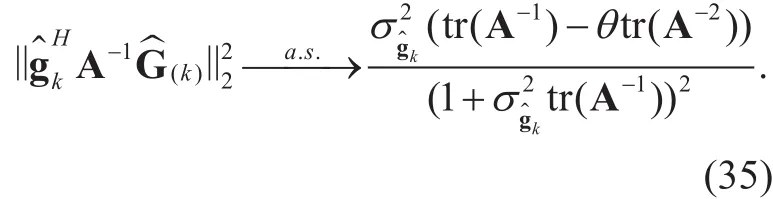
Next we focus on the quantization noise and white noise term. Note that in the massive MIMO system with large M and K, we can approximateas

The last step in (36) is due to

We can see from (30), (35) and (36) that the SINRkis related to the terms of tr(A−1) and tr(A−2). Fortunately, tr(A−2) is the derivative of −tr(A−1) and the term of tr(A−1) can be obtained by using the Stieltjes transform of. More precisely, by using the Stieltjes transform of matrix, we can further obtain

where ψ is the unique real positive solution of

where

Combining all the asymptotic equivalents obtain above, we can finally arrive Theorem 1.

Note that the asymptotic equivalent for the achievable rate in (28) includes implicit equation, which is dif ficult to obtain insights into the performance for the low-resolution massive MIMO systems. In order to simplify the analysis and obtain insights into the performance for the low-resolution massive MIMO systems, we consider the special case of ignoring the large scale fading coefficients and provide the asymptotic equivalent for the achievable rate as in Proposition 1.

Proposition 1: For the special case of d1= ...= dK=1, the asymptotic equivalent expression in (28) can be reduced as

where a and b are given by (42) and (43), respectively. And

P ro o f: I n t h e s p e c i a l c a s e o f d1= ...= dK=1, the Stieltjes transform of matrixat the point −θ converges to (42)shown below almost surely [28, Example2.8].Thus, by calculating the derivative of tr(A−1)along θ, we can obtain tr(A−2) as shown in(43) on the next page.

Therefore, in this case of d1= ...= dK=1,we derive the asymptotic equivalent of the achievable rate as in Proposition 1.

4.1 Performance evaluation

In this subsection, we will employ the asymptotic equivalent expression as in Proposition 1 to obtain the insights into the performance of the low-resolution massive MIMO system.

Remark 1: With fixed pp, pu, M and K,when the quantization resolution increase to in finity, then (41) reduces to

respectively. a1and b1are the same with (42)and (43), but replacing the parameters σ and θ with σ1and θ1, respectively.

This conclusion is reasonable because in the systems with the in finity resolution ADCs, the quantizer noise can be ignored (i.e., κ→1).We also notice that the quantization process affects both the desired signal term and the effective noise term since the parameters a, b and σ2contains the quantization factor κ.This implies that the quantization noise cannot be simply modeled as an additive noise that independent with the quantizer input signal as shown in [29].

Remark 2: With fixed M, K and quantization resolution, when the transmit power puand ppboth increase to in finity, then (41) converges to

respectively. a2and b2are the same with (42)and (43), but replacing the parameters σ and θ with σ2and θ2.

As we can see from (47) that the achievable rate is fixed when the transmit power increase to infinity and depends on the quantization factor κ. This implies that, in contrast to the traditional massive MIMO systems with infinite quantization resolution, the performance loss caused by the low-resolution ADCs cannot be compensated for by simply increasing the transmit power. Moreover, (48) reveals that when the pilot transmit power increase to in finity, the variance of the channel estimator converges to a fixed point. That is to say, in contrast to the traditional systems with in finite resolution ADCs, perfect CSI cannot be acquired by merely increasing the pilot transmit power in the low-resolution systems.

Next we will study how to compensate the performance loss due to the low-resolution ADCs. As it is known that for traditional massive MIMO systems, the achievable rate achieved by MMSE receiver will increase to infinity with increasing the transmit power,while the achievable rate saturates to a fixed point with in finite transmit power for low-resolution massive MIMO systems. Therefore,we will investigate the problem of how many more antennas would be needed in low-resolution massive MIMO systems to achieve the same achievable rate as that in traditional massive MIMO systems.

We assume that the number of antennas in low-resolution massive MIMO and traditional massive MIMO systems are Mlowand Mconv, respectively. We also assume that, in both scenarios, the number of users K is fixed,the transmit power of users is p, such that pp= pu= p and the training length τ=K.We aim to seek for the minimum value of Mlowsuch that both quantized and unquantized systems achieve the same achievable rate and provide the following optimization problem:

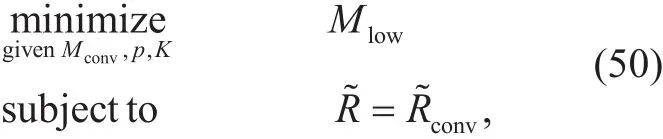
V. NUMERICAL RESULTS

In this section, numerical results are provided,where the low-resolution massive MIMO systems with K=50 and τ=K is considered.

Fig. 1. Average achievable rate versus the SNR with the number of antennas M =100 for different quantizers with 1, 2, 3 and ∞ bits.

Fig. 2. Average achievable rate versus the SNR with the number of antennas M =100 for different quantizers with 1, 2, 3 and ∞ bits.

We first evaluate the validity of the asymptotic equivalent for the achievable rate given in Theroem 1 and Proposition 1. Figure 1 and figure 2 show the average achievable rate versus the SNR with the number of antennas M=100 for four different quantizer bits with 1, 2, 3 and ∞ bits, where the solid lines represent the achievable rate plotted by using Monte-Carlo method, and the markers are calculated by using the asymptotic expression given in (28) and (41), respectively. The average achievable rate in both figures is given by

In figure 1, we assume the users are randomly distributed in a disk cell with the maximum radius of 1000m and the minimum radius of 100m. The large-scale coefficients are modeled by dk= zk/(rk/100)3.8, where zkis a log-normal random variable with standard derivation of 8dB and rkis the distance between the kth user and the BS. While in figure 2, the large scale coefficients for all users are assume to be equal, i.e., d1= ...= dK=1.It can be easily see from figure 1 and figure 2 that the results obtained by our analysis almost overlaps with the Monte-Carlo simulations.This verifies the accuracy of our obtained result in both (28) and (41).

We then compare the average achievable rate between the low-resolution and traditional massive MIMO systems. In figure 3, the average achievable rates versus the number of receive antennas for with transmit power pp= pu=0 dB is illustrated. We can see from figure 3 that, compared with the traditional system, the low-resolution massive MIMO systems can still achieve a reasonable high average achievable rate. For example, with M=200, the system with 1 quantization bits and 2 quantization bits can still achieve an average rate of 3.36 bits/s/Hz and 5.48 bits/s/Hz, respectively, which amounts to 54.9% and 87.8% of the average achievable rate of the traditional system. We can also see from figure 3 that we can increase the number of antennas at the base station to compensate for the performance loss due to the low-resolution ADCs.

In order to elaborate how to compensate the performance loss in low-resolution massive MIMO systems by increasing the number of antennas, Figure 4 illustrates the ratio of η=Mlow/Mconvwhen both low-resolution and traditional systems achieve the same achievable rate with the assumptions of Mconv=100 and K=50. We can see that in the low SNR region (i.e., SNR ＜ −10dB), the systems with 1-bit quantization needs to equip around 1.5 times more antennas to achieve the same average achievable rate as the traditional systems, while for the systems with 2-bit quantization bits, the ratio decrease to 1.1.This is because that with higher quantization bits, the performance loss is less. Moreover,as the SNR grows large, the ratio also goes to in finity. This is because that the achievable rate of the traditional systems increase to infinity with the increasing SNR. However, as shown in Remark 2, the achievable rate of the low-resolution systems saturates to a fixed point even if the SNR increases to in finity.

VI. CONCLUSIONS

In this paper, we investigated the uplink achievable rate performance of the low-resolution massive MIMO systems. By using the AQNM,we derived a tight asymptotic equivalent for the uplink achievable rate with a proper designed MMSE receiver assuming imperfect CSI is known at the BS. It was shown that the performance loss due to the low-resolution quantization is not as severe as might be imagined.Numerical results demonstrated that for 2-bit quantization systems, only 1.1 times more antennas are needed to be installed at the BS for low-resolution massive MIMO systems such that the performance loss can be compensated.

ACKNOWLEDGEMENTS

This work was supported by the Beijing Natural Science Foundation under Grant No.L172030, the Beijing Municipal Natural Science Foundation under Grant No. 4174102,NSFC Project under Grants No. 61471027, the National Natural Science Foundation of China under Grant No. 61701017 and Grant No.61601018, the Open Research Fund through the National Mobile Communications Research Laboratory, Southeast University, under Grant No. 2017D01.

Fig. 3. Average achievable rate versus number of receive antennas for different quantizers with 1, 2 and ∞ bits with average transmit power pp = pu = 0dB.

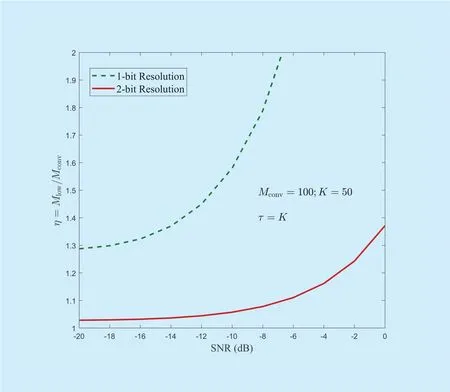
Fig. 4. The ratio of = Mlow=Mconv versus SNR with Mconv = 100 and K = 50 for different quantizer bits.