基于优化最小化的加强稀疏性的稀疏信号恢复算法

王 琛,方 勇, 黄青华,张立明

(1.上海大学通信与信息工程学院,上海200444;2.澳门大学科学与技术学院,澳门999078)

非零元素个数远远小于其向量维度的稀疏信号的恢复问题[1]在信号处理领域受到高度关注,并成功地应用于大规模天线阵列的无线信道估计[1-2],水声信道[3-4]估计和生理信号的节能远程观测[5]中.利用远小于其向量维度的观测准确地恢复稀疏信号的本质是对欠定的线性系统求最优稀疏解[6].

目前,稀疏信号恢复算法主要分为两大类.第一大类算法是基于凸松弛的方法,这类算法用L0范数的近似,即L1范数作为稀疏惩罚函数,从而将基于L0范数的稀疏信号恢复问题转化为可以追踪并求解的凸优化问题,其中包括基追踪[7]以及高效的基于交替方向乘子(alternating direction method of multiplier,ADMM)的最小绝对收缩和选择算子(least absolute shrinkage and selection operator,LASSO)算法[7-8].第二大类算法是基于贪婪追踪(greedy pursuit)的方法,包括正交匹配追踪(orthogonal matching pursuit)[9]及其最近针对特定应用背景而发展的改进算法,如改进子空间追踪[10].贪婪算法使用迭代方式确定非零元素,在每一次迭代中选择和当前残差最相关的一个或多个元素,并且这一相关性是使用基于L2范数的内积的绝对值来衡量的.上述两类方法分别通过L1范数和L2范数对L0范数进行松弛,虽然能够达到恢复稀疏信号的目的,但由于对于待恢复信号的稀疏约束性不够强,导致基于L1范数的稀疏优化方法容易倾向于较大值的元素,而基于L2范数的方法容易受到异常值的影响.

近年来,为了获得比L1范数和L2范数对L0范数更好的近似,利用非凸稀疏惩罚函数恢复稀疏信号的方法引起了广大学者的关注.这类算法主要使用非凸的Lp(0＜p＜1)范数作为惩罚函数来恢复稀疏信号.L1范数是凸的,而Lp(0＜p＜1)范数是非凸的,这就使得目前很多基于凸分析的理论不能再应用于基于Lp(0＜p＜1)范数的稀疏信号恢复问题,从而导致算法解的唯一性和算法的收敛性都变得难以保证,并且算法十分复杂.虽然利用非凸稀疏惩罚函数增加了算法设计的难度,但是Lp(0＜p＜1)范数比L1范数对L0范数有更好的近似,因此能够取得更好的稀疏信号恢复性能[11].为了得到基于Lp(0＜p＜1)范数的稀疏恢复问题的闭式解,Chartrand[12]提出用迭代p-收缩算法(iterative p-shrinkage algorithm)进行稀疏信号的恢复,并进一步证明了这一算法的收敛性[13].值得注意的是,迭代p-收缩算法作为迭代软阈值算法(iterative soft thresholding algorithm,ISTA)[14]的拓展,其本质是对目标函数的凸部分建立一阶近端凸上界[15],再对这一凸上界进行迭代求解,从而最终得到原稀疏信号的估计值.虽然Woodworth等[13]证明了如果算法收敛到全局最优点,那么这一全局最优点即是原稀疏信号,但是由于目标函数本身含有非凸部分,迭代p-收缩算法只能收敛于平稳点,而这一平稳点是局部最优解,并非全局最优.对于目标函数中含有非凸函数的优化算法,目前均无法保证算法收敛于全局最优.算法能够收敛于平稳点,即局部最优解,已经是目前理论所能达到的最好结果[15].因此,算法局部最优解的优劣对算法的性能起着决定性影响.目前,迭代p-收缩算法的局部最优解主要有以下问题:第一,局部最优解受参数p的影响,在0＜p＜1时,不能有效地确定最优的p值,且当p值选取不恰当时,算法局部最优解的性能会有所下降[16];第二,在进行迭代学习时,由于迭代收缩算法的特性,梯度下降方向只在目标函数的凸部分,而没有包含目标函数的非凸部分,这导致迭代p-收缩算法在迭代过程中容易收敛到性能较差的局部最优解.

基于稀疏贝叶斯学习的稀疏信号恢复算法在很多应用领域取得了比基于L1范数和L2范数算法更好的稀疏信号恢复效果[17-20].这是因为稀疏贝叶斯学习使用的收缩函数可以有效地降低算法对错误信号的估计倾向,并且只需要估计信号的噪声参数,而不受参数p的影响.但是稀疏贝叶斯学习要求预先了解信号及噪声的先验概率密度函数,这大大局限了该算法的应用范围.为了利用稀疏贝叶斯学习收缩函数的优势,同时又不受局限,在了解稀疏贝叶斯学习收缩函数的情况下,可以通过改进现有的迭代p-收缩算法对稀疏信号进行求解.但是迭代p-收缩算法是基于ISTA的,在迭代学习中梯度下降的方向只在其凸部分,而忽略了非凸部分,从而容易收敛于性能较差的局部最优解.为了提高稀疏信号的恢复性能,了解稀疏贝叶斯学习所对应的惩罚函数的显式对改进稀疏恢复算法,从而提高恢复性能至关重要.事实上,迭代p-收缩算法也是在了解惩罚函数的显式即Lp(0＜p＜1)范数的基础上,通过对其目标函数的凸部分进行近端上界近似后,再进行优化求解得到的.

为了突破上述稀疏信号恢复算法的缺点,提高稀疏信号的恢复性能,本工作利用收缩函数和惩罚函数的关系,基于稀疏贝叶斯学习中使用的收缩函数得到了一种新的非凸稀疏惩罚函数,然后将这一非凸稀疏惩罚函数作为惩罚函数加强恢复信号的稀疏性,利用优化最小化(majorization-minimization,MM)算法对这一非凸惩罚函数建立凸上界,并对这一凸上界和目标函数的凸部分同时进行迭代求解,得到最后的恢复信号.相比其他稀疏信号恢复算法,本工作提出的非凸的稀疏惩罚函数比L1范数对L0范数有更严格的逼近,即比L1范数拥有更强的稀疏约束性,也不似Lp(0＜p＜1)范数受参数p的影响.为了解决基于ISTA的迭代p-收缩算法中梯度下降方向只包含目标函数凸部分这一问题,本工作利用MM算法对目标函数中的非凸惩罚函数建立凸上界,这就使得迭代优化过程中梯度方向同时包含目标函数的凸部分和非凸部分,从而使提出的算法收敛于更好的局部最优解,提高了稀疏信号的恢复性能.最后,将提出的算法应用于稀疏无线信道的估计问题,仿真实验的结果表明,算法在噪声环境下可以用更少的导频,取得更准确的信道估计结果.

1 加强稀疏性的非凸惩罚函数

1.1 稀疏信号恢复

稀疏信号的恢复问题可以转化为对如下目标函数进行优化的问题,即有

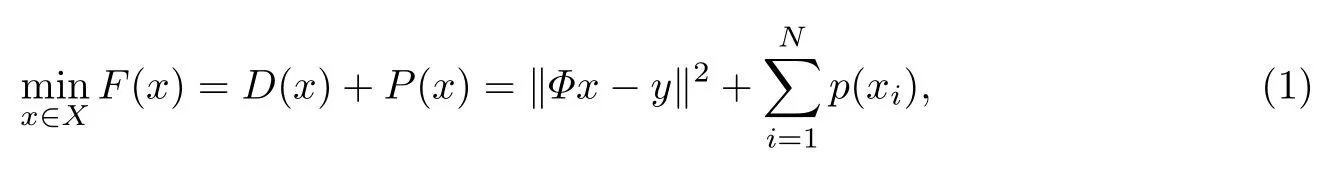
式中,向量x∈RN×1为未知的稀疏信号(L0范数为M ≪N的测量矩阵,向量y∈RM×1为测量结果,凸函数为数据保真函数,为惩罚函数.在稀疏信号恢复问题中,P(x)的作用是约束x的稀疏性,使恢复出的信号x的非零元素的个数远远小于其维度.通过式(1),稀疏信号恢复的问题转化为已知y和Φ的情况下优化求解问题(1)从而恢复出x的问题.

1.2 收缩函数和惩罚函数的关系

为了更好地说明惩罚函数的作用,考虑标量形式的带有惩罚函数的优化问题,即已知求解使得如下目标函数最小:

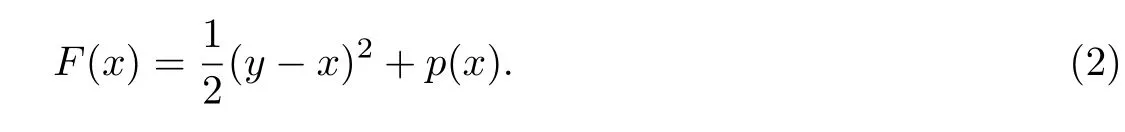
为了突出目标函数对x求最小值时和y的关系,定义

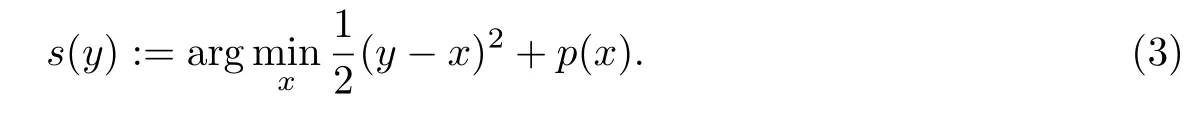
s(y)就是收缩函数,这是因为在稀疏信号恢复问题中,s(y)使得y向0收缩.为了得到收缩函数和惩罚函数的关系,对F(x)求关于x的导数,可得,

令导数为0,可得

即

1.3 惩罚函数

传统的L1范数的惩罚函数为p1(x)=λ|x|,其收缩函数为软阈值函数,定义为

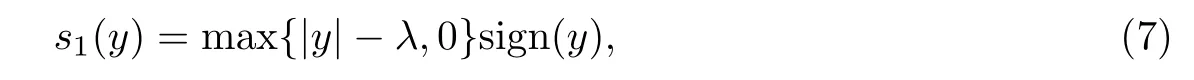
将p1(x)=λ|x|带入式(1),则需要优化的问题变为直观上,λ的作用是控制稀疏性和数据保真性之间的权重,但本质上主要目的是为了对抗噪声.由式(7)容易发现,满足|y|＞λ的估计值y会被当作待恢复的原信号保留,而不满足|y|＞λ的估计值y会被当作噪声滤掉,因此λ也被称为噪声参数[17].

由式(7)可以发现,软阈值函数的估计倾向于具有较大值的元素,这就导致原信号中的非零元素由于具有较小的值而被忽略,而较大值的噪声元素会被重点估计.

非凸的Lp(0＜p＜1)范数的惩罚函数为其收缩函数为p-收缩函数,即

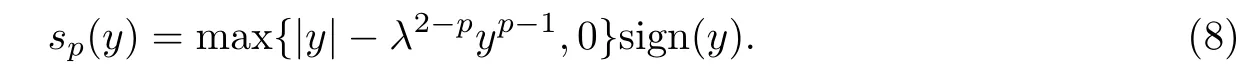
由式(8)可以发现,p-收缩函数受参数p的影响.参数p不同对恢复算法的性能影响不同,当选择不恰当的参数p值时,算法性能会有所下降[16].

稀疏贝叶斯学习比传统的基于L1范数的优化方法有更好的稀疏信号恢复性能[17].特别地,当观测矩阵正交时,稀疏贝叶斯学习中使用的收缩函数为

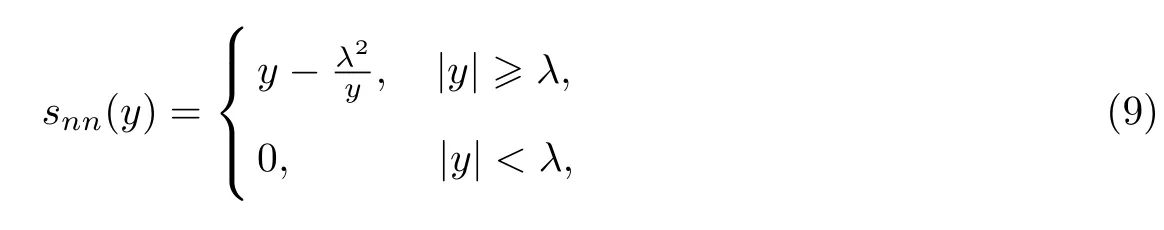
即非负garrote函数[21].由式(9)可以发现,非负garrote函数中λ2在收缩函数的分子上,这就导致收缩函数snn(y)对较大值的元素有较小的倾向性,从而使得稀疏贝叶斯学习在很多应用中得到了比传统L1范数更好的稀疏信号恢复结果[17-20].

为了利用稀疏贝叶斯学习中的收缩函数snn(y)提高稀疏优化问题解的准确性,需要求得snn(y)对应的惩罚函数pnn(x)的显式.文献[17-20]中的稀疏贝叶斯学习框架并未给出对应惩罚函数pnn(x)的表达式.下面利用收缩函数和惩罚函数的关系,即式(2)∼(6),由snn(y)得到对应的pnn(x),从而提出了一种新的惩罚函数.

将式(10)代入式(6),可得

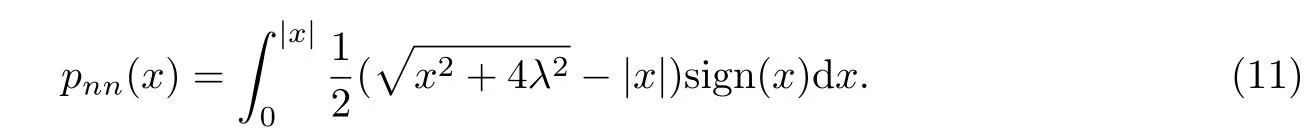
进一步求解式(11),可得

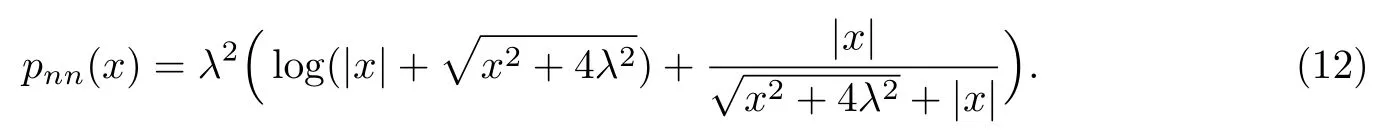
式(12)即为snn(y)对应的惩罚函数pnn(x)的显式.

我们都知道识字写字教学在小学语文教学中占有极其重要的基础地位，因此，我们需要扎实上好每一堂识字写字课。汉字教学不同于普通的汉字研究，而小学生的记忆、想象、思维及其他活动主要基于图像。在识字教学中，我们需要挖掘汉语言文字在几千年历史发展中积累的大量文化信息，从而增加识字教学的知识内容。整个过程应该集科学、知识和趣味为一体，也让学生进一步感受语言文字的独特魅力。

1.4 惩罚函数的增强稀疏性

对pnn(x)在x∈(0,∞)上求导数,可知一阶导数在x∈(0,∞)上是严格大于0的,二阶导数在x∈(0,∞)上是严格小于0的.因此,对于是非递减的严格凹函数,这使得pnn(x)可以促进稀疏性,并比L1范数对有更严格的逼近[17].可以发现,总是存在一正常数R＜∞,使得实数域中对于任一以0为中心,以r＞R为半径的球面Sr内满足

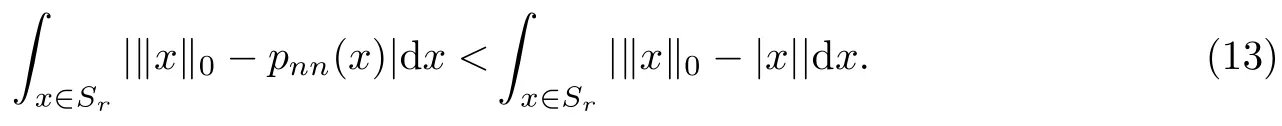
由式(13)可以看出,只要对足够的区域取平均,就可以使pnn(x)逼近‖x‖0的误差比|x|逼近的误差小.另外,噪声参数λ的引入也可以增加pnn(x)的稀疏性.式(12)可以变换为

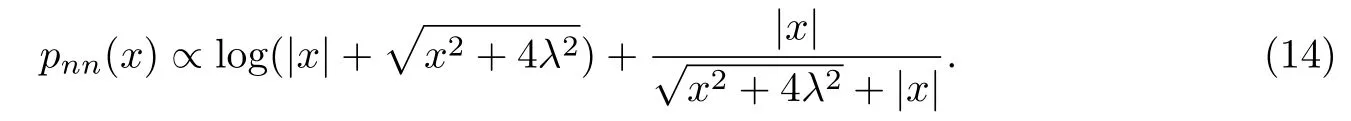
可以发现,当λ→0时,式(14)的第一项趋近于log(|x|),第二项趋近于也是对的一种较|x|更严格逼近,这是因为而但是λ并不能取0,这是因为由式(12)可知,当λ=0时惩罚函数将失去作用,从而无法促进稀疏性.同时,由式(9)可知,如果λ小于噪声值,噪声信号将无法被滤掉,从而降低了算法的性能.综上所述,λ的理想取值应为大于或等于噪声的最小值.

由以上分析可知,本工作提出的非凸惩罚函数pnn(x)比L1范数|x|对‖x‖0有更小的逼近误差,即比L1范数|x|有更强的稀疏约束性,同时不似Lp(0＜p＜1)范数受参数p的影响.

2 非凸稀疏信号恢复算法

使用L1范数|x|作为惩罚函数的稀疏信号恢复问题本质上是一个凸稀疏优化问题.在本工作中,由于使用加强稀疏性的非凸函数pnn(x)作为惩罚函数,稀疏信号的恢复问题就变成了一个非凸稀疏优化问题.因此,常规的凸优化算法无法解决这一问题.另外,目前基于迭代软阈值算法的迭代p-收缩算法中,梯度下降方向只包含目标函数的凸部分,从而导致算法容易收敛于性能较差的局部最优解.因此,本工作利用MM方法解决以上问题.

2.1 非凸稀疏优化数学模型

基于非凸惩罚函数的稀疏信号恢复问题可以表达为[22]

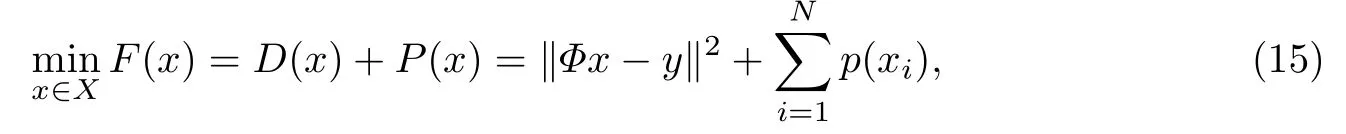
2.2 迭代p-收缩算法

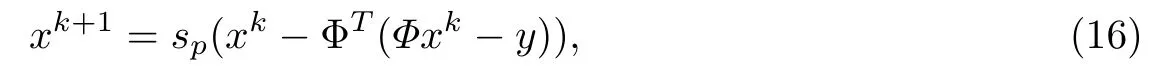
式中,sp是pp(x)对应的收缩函数(见式(8)),xk是在第k次迭代中产生的最优点.由式(16)可知,这一梯度迭代方法可以看作是在xk处先进行线性化函数D(x)的近端正则化[14],再求其最小值,如下式所示:

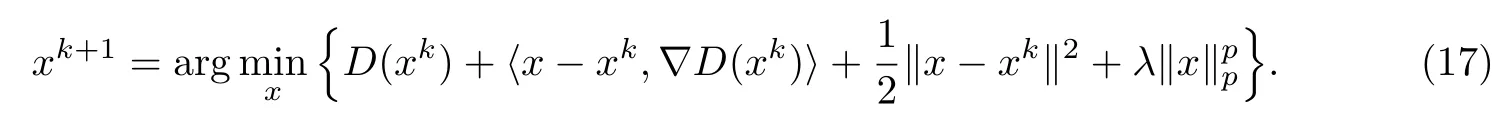
由式(16)和(17)可以发现,基于ISTA的迭代p-收缩算法的实质是对原非凸目标函数在其凸部分D(x)=‖进行近端上界近似后,再经由收缩函数sp滤波,最终得到第k次迭代中的估计点.这是一种拓展的ISTA,其中目标函数的下降梯度只包含凸部分,而不包括非凸部分.非凸部分产生的收缩函数只起滤波作用.直观地,如果梯度下降中得到的估计点含有误差,那么对错误的估计再进行稀疏滤波也很难进一步提高算法的性能.为了解决这一问题,本工作提出用MM算法对目标函数的非凸部分建立近似凸上界,同时在梯度学习中考虑目标函数的凸部分和非凸部分,从而提高稀疏信号恢复算法的性能.

2.3 加强稀疏性的稀疏信号恢复方法

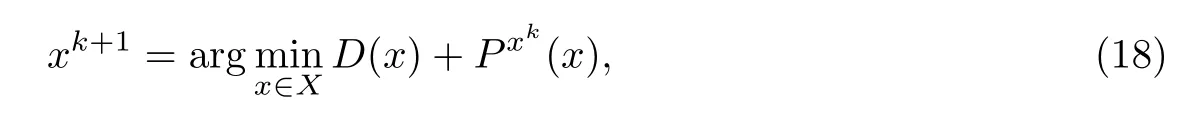
式中,xk是在第k次迭代中产生的最优点,Pxk(x)是在xk的Majorization函数.在MM算法中,Pxk(x)通常是P(x)的凸上界近似,且在x=xk时与P(x)相等,即

因为D(x)和Pxk(x)都是凸的,所以式(18)可以用Fermat定理求解[23].

定理1 令(xk)k∈N是由式(18)产生的解,那么序列(F(xk))k∈N单调递减且收敛.

这里使用局部二次近似寻求P(x)的凸上界,因为该近似方法有较好的性能表现[24].由p(x)的非凸性(式(15))可得

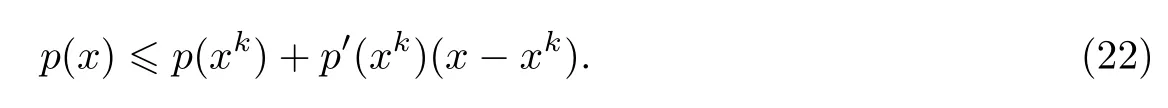
将式(22)和(23)联立,并经过简单变换可以得到凸上界近似为

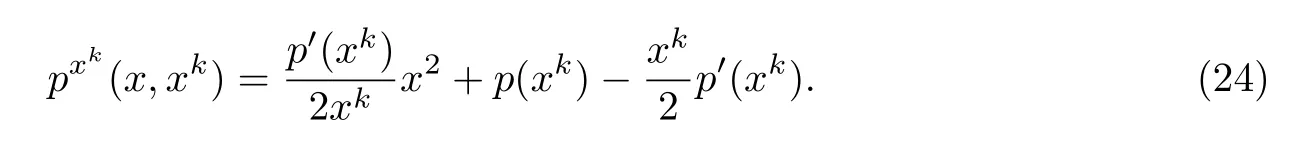
式(24)对应的矩阵形式为

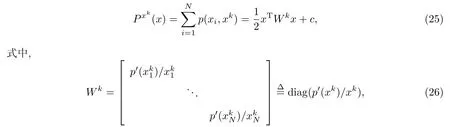
c是与x无关的常数.因此在第k次迭代,稀疏信号恢复问题变为如下优化问题:

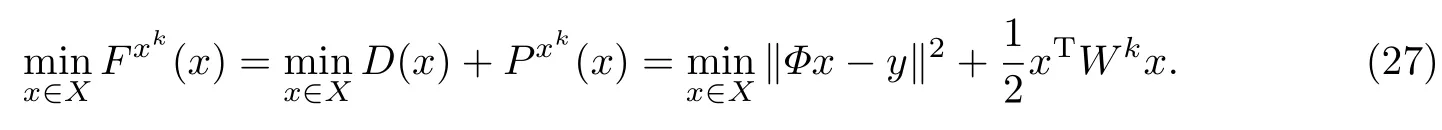
与基于ISTA的p-收缩算法使用非凸的pp(x)=λ‖x‖pp作为稀疏惩罚函数不同,这里使用式(12)表示的非凸的pnn(x)作为稀疏惩罚函数.现将本工作提出的加强稀疏性的稀疏信号恢复算法(E-sparse算法)的实现步骤总结如下.

步骤1 初始化,给定任一初始点x0.

步骤3 在第k次迭代中,令

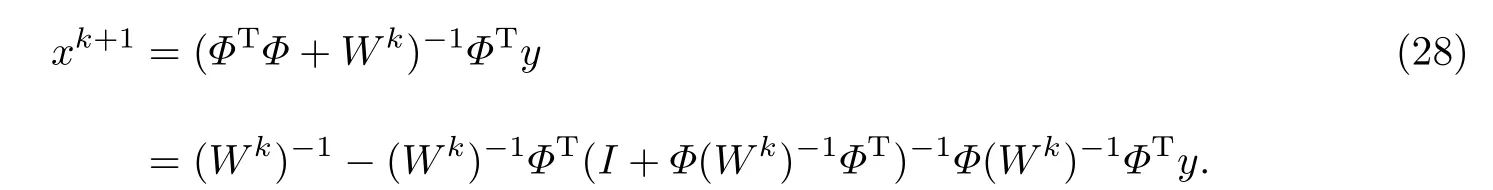
步骤4 若达到迭代次数要求或算法收敛,则停止迭代,输出恢复的稀疏信号xk+1;否则转到步骤3继续执行.

通过观察可以发现,在迭代过程中,E-sparse算法的优化梯度方向同时包含目标函数的凸部分和非凸部分(即Wk).

3 仿真实验与分析

下面通过仿真实验验证E-sparse算法的优越性.将提出的E-sparse算法应用于稀疏无线信道的估计[25].稀疏无线信道估计的数学模型可以表示为

式中:A是Nr×Nh维的导频矩阵,且Nr≪Nh;h是Nh×1维的信道增益矩阵;n为加性高斯白噪声.通过分析和实际测量可知,在大部分情况下,无线信道通过特定变换后是稀疏或近似稀疏的,这使得h中大部分元素为0,只有很少一部分元素非0.非零元素的个数即稀疏无线信道矩阵h的稀疏度,可以用S表示.式(29)可以转化为对以下优化问题的求解:

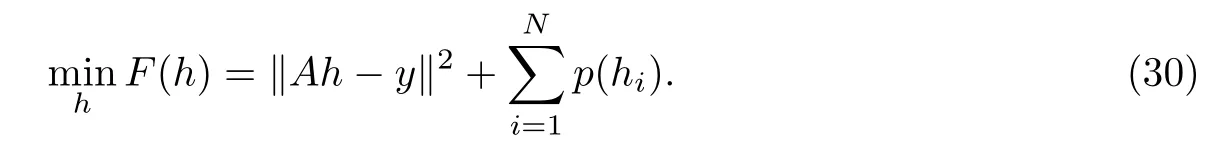
式(30)和(15)具有相同的形式,可以用E-sparse算法进行求解.为了满足稀疏恢复的有限等距性质(restricted isometry property,RIP)条件,令矩阵并对进行列归一化,得到最后的导频矩阵A.稀疏无线信道h的Nh=180,S=12.噪声n∼N(0,σ2I).

使用归一化均方误差(normalized mean square error,NMSE)衡量算法对于无线信道估计的性能,即NMSE=其中是原始无线信道h的估计值.设置ADMM算法和E-sparse中的λ=0.05.令E-sparse算法的初始估计为使用导频得到的小二乘解,并设置最大迭代次数kmax=50.

使用以下算法进行实验并进行比较:①基于L1范数的ADMM-LASSO算法[7];②基于L2范数的正交匹配追踪算法(orthogonal matching pursuit,OMP)[9];③基于Lp范数的迭代p-收缩算法.为了验证迭代p-收缩算法的性能受参数p的影响,令p=0.1,0.3和0.7.与文献[13]相同,这里也使用基于ADMM的迭代p-收缩算法,该算法和AMDD-LASSO的不同之处在于使用的收缩函数为式(8).

3.1 噪声对无线信道估计性能的影响

图1为E-sparse算法与AMDD-LASSO,OMP在不同噪声方差时的性能比较,其中Nr=45.从图1中可以看到,迭代p-收缩算法虽然比基于L1范数的ADMM-LASSO算法有更好的性能表现,但随着噪声的变化,算法表现不稳定,即没有一个稳定的p值可以一直取得比其他p值更好的算法性能,即算法受p值的影响.E-sparse算法的估计误差比其他算法明显要小,估计性能具有明显优势.E-sparse算法对ADMM-LASSO和OMP的优势说明了使用非凸的惩罚函数增强稀疏约束性的优势.E-sparse算法与基于Lp范数的迭代p-收缩函数算法相比较,其优势表明:①非凸的稀疏增强函数不受参数p影响,性能表现稳定;②基于MM方法的E-sparse算法,在迭代学习中下降梯度同时包含目标函数的凸部分和非凸部分,能够在第k次迭代中得到性能更好的估计点.

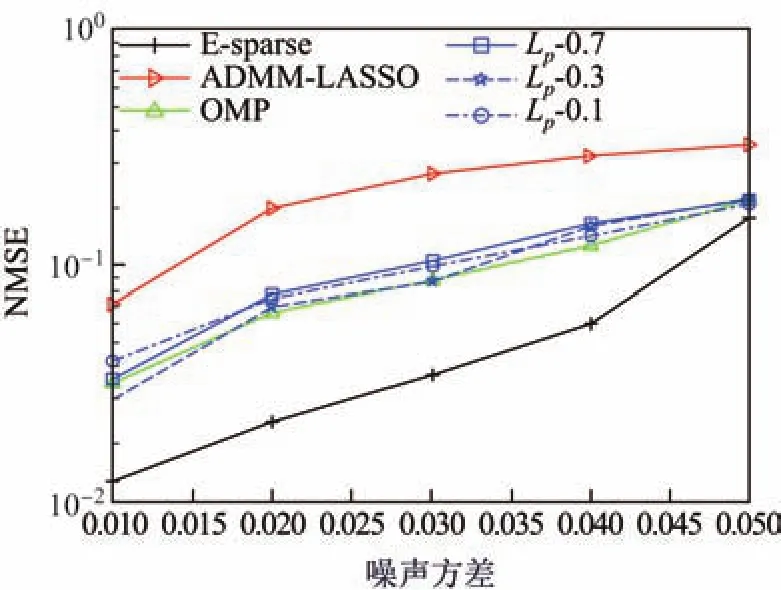
图1 NMSE随噪声方差的变化Fig.1 NMSE versus noise variance

3.2 导频比例对算法性能的影响

图2所示为E-sparse算法与AMDD-LASSO,OMP,迭代p-收缩算法(Lp-0.1,Lp-0.3和Lp-0.7)在导频比例Nr/Nh不同时的性能比较,其中Nr/Nh为10%∼35%,噪声方差σ2=0.01.从图2可以看出,E-sparse算法在噪声环境下可以用更少的导频,得到更准确的信道估计结果.另外,迭代p-收缩算法除了在Nr/Nh=0.25时比AMDD-LASSO具有明显优势之外,在其他导频比例时,优势并不明显.在Nr/Nh=0.2时,迭代p-收缩算法比ADMM-LASSO性能更差.与之前的仿真结果相似,由于估计效果受p值的影响,基于迭代p-收缩算法无法选出最优的p值.

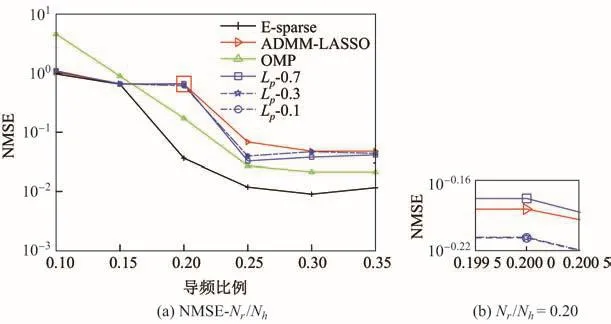
图2 NMSE随Nr/Nh的变化Fig.2 NMSE versus the ratio of Nr/Nh

4 结束语

本工作通过分析收缩函数和惩罚函数的关系,从稀疏贝叶斯学习使用的收缩函数中得到了一种新的非凸稀疏惩罚函数.这一非凸惩罚函数比L1范数拥有更强的稀疏约束性,即对L0范数有更好的逼近,也不似Lp范数受参数p的影响.由于引入了新的非凸稀疏惩罚函数,目标函数变为难以求解的非凸目标函数.为了解决非凸目标函数的优化问题,提出利用MM算法.由于MM算法迭代的优化梯度方向同时包含目标函数的凸部分和非凸部分,因此得到了比基于ISTA的迭代p-收缩算法更好的性能表现.特别地,将提出的算法应用于稀疏无线信道的估计问题,仿真结果表明本算法在在噪声环境下可以用更少的导频,取得更准确的信道估计结果.

由于基于非凸函数的优化算法理论上只能收敛于局部最优解,探索基于MM方法的局部最优解和全局最优解的关系,并使局部最优解尽可能的接近全局最优解,从而提高稀疏信号的恢复性能,将是以后研究的重点.