基于直觉模糊集的模糊C均值聚类改进算法

李 婧,于丽英

(上海大学管理学院,上海200444)

在科学研究中,人们常常需要把研究对象按照它们的自身性质和用途等进行分类,以便进一步研究.聚类分析是指对具体或抽象事物进行分类,使得同类事物之间具有极高的相似度,而不同类事物之间高度相异.模糊C均值(fuzzy C-means,FCM)算法是一种常用的聚类分析方法,最早由Dunn[1]提出.之后,Bezdek[2]对FCM聚类算法进行了推广.目前,FCM聚类算法已在医疗图像分割[3]、环境污染状况分类[4]、水下目标识别[5]和电力客户分类[6]等领域得到了广泛应用.

传统的FCM算法中聚类对象的特征值通常是精确值,而在许多实际问题中,聚类对象的信息是模糊的,因此模糊环境下的FCM聚类算法被很多学者关注.于春海等[7]提出了聚类对象具有不确定性区间数多指标信息的聚类分析问题的算法.张洪美等[8]提出了基于直觉模糊集的聚类方法,但当样本数量较大且实时性要求较高时,该方法无法满足需要.吴成茂[9]提出了基于直觉模糊集的FCM聚类算法,但该算法随机选择初始聚类中心,鲁棒性较差.申晓勇等[10]和昌燕等[11]分别研究了基于直觉模糊集的FCM聚类算法初始聚类中心的选择问题,但均未考虑聚类样本的特征权重对聚类结果的影响.目前,已有很多学者将基于直觉模糊集的FCM聚类方法应用现实问题中.王昭等[12]提出了一种融入局部信息的直觉模糊C均值聚类算法,并应用于图像分割领域.耿秀丽等[13]将直觉模糊C均值聚类方法应用于客户聚类和识别中.针对上述研究中未同时考虑特征权重和初始聚类中心的问题,本工作提出了一种改进的基于直觉模糊集的FCM聚类算法.

1 预备知识

1.1 直觉模糊集

Atanassov[14]首次提出了直觉模糊集的概念,并利用隶属度与非隶属度两个标度刻画数据的模糊性.

定义1[14]令集合X={x1,x2,···,xn},X上的一个直觉模糊集可表示为

式中,µA(xi)∈[0,1],νA(xi)∈[0,1]分别表示元素xi对A的隶属度与非隶属度,且对于∀xi∈X,都有0≤ µA(xi)+νA(xi)≤ 1.记πA(xi)=1−µA(xi)−νA(xi)为犹豫度,则πA(xi)∈[0,1].

定义2[15]设A={〈xi,µA(xi),νA(xi)〉|xi∈ X}和B={〈xi,µB(xi),νB(xi)〉|xi∈ X}为两个直觉模糊集,则直觉模糊集A与B的欧氏距离为

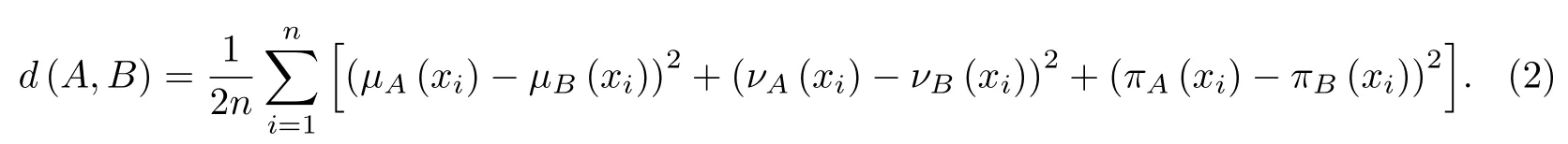
由X中的元素xi对A的隶属度和非隶属度所组成的有序对〈µA(xi),νA(xi)〉称为直觉模糊数[16].为方便起见,直觉模糊数记为〈µi,νi〉,犹豫度记为πi.

定义3[16]设为直觉模糊数,则有

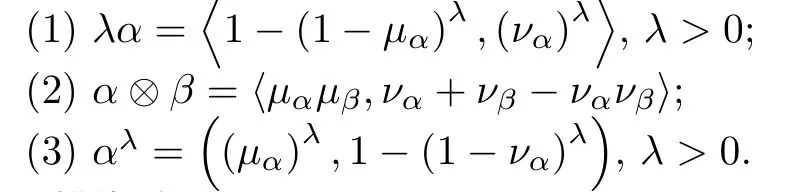
1.2 模糊熵

直觉模糊熵是直觉模糊集理论中的一个重要概念,由Burillo等[17]最先给出定义.直觉模糊熵是一种反映直觉模糊集模糊程度的量化指标.

定义4[18]设F(X)表示非空集合X上的所有直觉模糊集的集合,直觉模糊集A∈F(X),称函数E:F(X)→[0,1]为直觉模糊集A的直觉模糊熵E(A),则有

(1)E(A)=0,当且仅当∀x ∈ X,〈µA(x),νA(x)〉= 〈1,0〉或〈0,1〉;

(2)E(A)=1,当且仅当∀x ∈ X,〈µA(x),νA(x)〉= 〈0,0〉;

(3)E(A)=E(Ac);

(4)∀A,B ∈F(X),若A⊆B,则E(A)≤E(B).

定义5[19]设X={x1,x2,···,xn}为非空集合,A∈F(X),则有

式中,E(A)为A的直觉模糊熵.

2 改进的FCM聚类算法

2.1 问题描述

设有限集Y={y1,y2,···,yn}是n个待聚类样本组成的集合,G={g1,g2,···,gs}为样本的s个特征组成的特征集.P=(P1,P2,···,Pn)T为样本的特征值矩阵,Pi=(pi1,pi2,···,pis),i=1,2,···,n是样本yi的特征矢量,pij(i=1,2,···,n,j=1,2,···,s)是样本yi关于特征gj的特征值.c(c＜ n)为聚类类别数,Z={Z1,Z2,···,Zc}是聚类中心集,Zk=(zk1,zk2,···,zks),k=1,2,···,c是聚类中心.U=[uik]n×c是划分的隶属度矩阵,uik∈ R是样本yi关于聚类中心Zk的隶属度.d(Pi,Zk)是yi的特征矢量Pi和聚类中心Zk间的欧式距离.m为模糊度参数,表示聚类效果的模糊程度,其值越大,聚类结果越模糊.由于目前尚无被广泛接受的模糊度参数,在FCM算法中常取m=2[20].定义样本集Y对于聚类中心集Z的广义欧氏距离平方和为

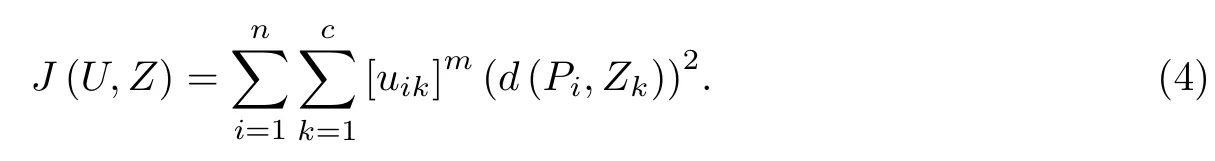
传统的FCM聚类算法有3点不足:①聚类样本yi(i=1,2,···,n)关于特征gj(j=1,2,···,s)的特征值pij都是精确数值,而现实中聚类问题的复杂性、多样性使得决策者很难给出精确数值;②未考虑样本特征权重对聚类结果的影响;③对初始聚类中心敏感.

因此,本工作提出一种改进的FCM聚类算法,对一个待聚类的样本集Y={y1,y2,···,yn}合理分类,其中样本Y的s个特征组成的特征集为G={g1,g2,···,gs}. 样本yi关于特征gj的特征值为直觉模糊数形式pij= 〈µij,νij〉,i=1,2,···,n,j=1,2,···,s, 其中µij,νij∈R+.样本的直觉模糊数特征值已知,而样本特征权重未知.

2.2 计算加权样本特征值

模糊熵描述了模糊集合的模糊程度和不确定程度.如果集合越模糊,它的模糊熵就越大,权重就越小;反之亦然.样本的特征权重必须反映各特征的相对重要程度.为避免赋权过程中的主观随意性,本工作采用直觉模糊熵确定特征gj的权重wj,有

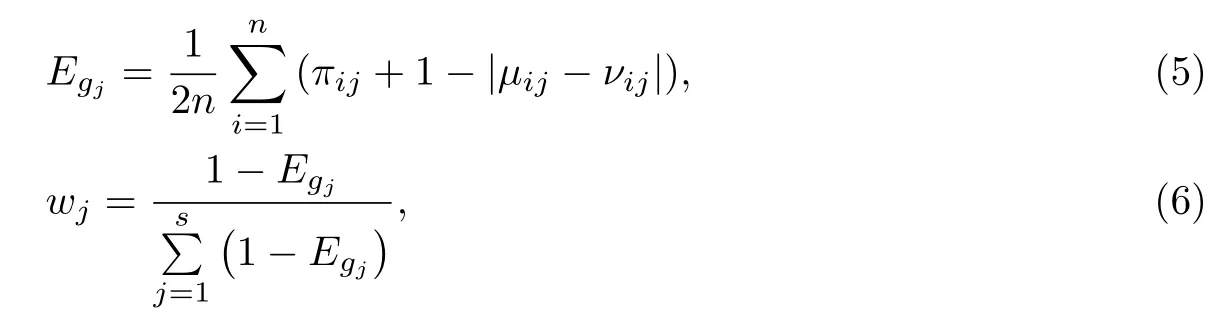
式中,犹豫度πij=1−µij−νij.Egj反映了样本集Y在特征gj下的特征值的模糊性和不确定性.Egj的值越大,模糊程度越高,说明聚类结果对特征gj的依赖程度越小.

此时,样本yi所对应的加权后的特征矢量为

2.3 确定初始聚类中心

由于传统的FCM算法对初始聚类中心敏感,不同的初始聚类中心往往对应不同的聚类结果.若利用欧氏距离作为距离度量工具,选择待聚类样本集中相互距离最远的c个样本的特征值为初始聚类中心,则有时会取到噪声点,从而影响聚类结果.袁方等[21]为消除传统的FCM算法对初始聚类中心的敏感性,定义了聚类对象的密度参数,有效地避开噪声点.赖玉霞等[22]提出采取对象分布密度方法确定初始聚类中心.本工作认为,在直觉模糊的大环境下,可以将初始聚类中心的选择区域进行密度细分,有效避开低密度区域的噪声点,取高密度区域中相互距离最远的c个点.

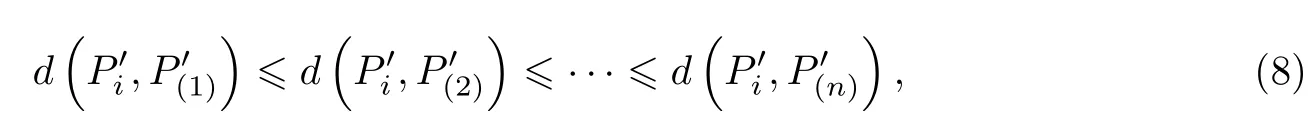
式中,0＜C＜n且为整数,具体数值视情况而定.ρi越大,说明的区域密度越大;反之,ρi越小,说明的区域密度越小.

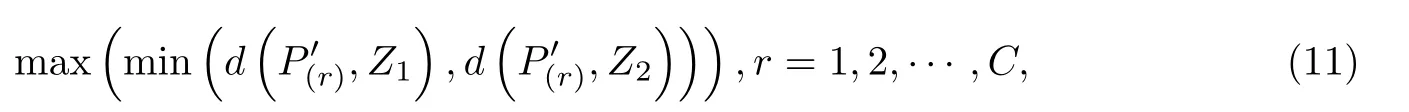
的特征矢量为第三个聚类中心Z3;最后,计算H中所有特征矢量到Z1,Z2,···,Zk−1的距离,在H中取出满足

的特征矢量为第k个聚类中心Zk(k=1,2,···,c).依此求得聚类中心Z={Z1,Z2,···,Zc},其中c个聚类中心取自特征矢量集H中的C个特征矢量.在确定初始聚类中心时,要避免过于集中,且H中的特征矢量的选取要避开噪声点.本工作中取C∈((n+c)/2,n)且为整数.

2.4 更新聚类中心和隶属度矩阵

在基于直觉模糊集的FCM聚类算法中,需要利用聚类中心计算对应的隶属度矩阵.

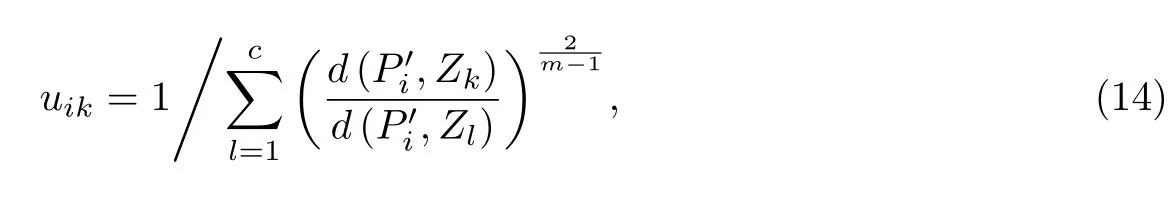
式中,m为模糊度参数.

利用隶属度矩阵更新聚类中心[9],其中第k个聚类中心记为Zk,

式中,

此时,样本集Y对于聚类中心Z的广义欧氏距离平方和[9]为

2.5 算法步骤

改进的FCM聚类算法的具体步骤如下.

步骤1 输入样本特征值矩阵P,聚类数目c,模糊度参数m,停止迭代的阈值ε,迭代次数δ.

步骤2 采用式(5)和(6)计算特征权重,再采用式(7)计算加权特征值矩阵P′.

步骤3 令t=0,确定初始聚类中心Z(t),并采用式(13)和(14)计算出隶属度矩阵U(t).

步骤4 判断t是否小于δ.若是,继续步骤5;若不是,跳转到步骤7.

步骤5 令t=t+1,采用式(12)更新聚类中心Z(t),再采用式(13)和(14)更新隶属度矩阵U(t).

步骤 6 采用式(18)计算J?U(t−1),Z(t−1)?和J?U(t),Z(t)?, 判断J?U(t−1),Z(t−1)? −J?U(t),Z(t)?＜ε是否成立.若成立,继续步骤7;若不成立,跳转到步骤4.

步骤7 输出隶属度矩阵U和聚类中心Z.

3 算例验证

文献[8]最早研究了基于直觉模糊集的聚类问题,因此本工作选取其中的算例进行验证.某汽车市场欲对5款不同的汽车Y={y1,y2,···,y5}进行分类,每款汽车有6个可供评价的特征G={g1,g2,···,g6},其中g1为燃料消耗量,g2为摩擦系数,g3为价格,g4为舒适度,g5为设计,g6为安全系数.每种汽车在各特征下的特征值用直觉模糊数表示,那么该聚类样本的特征值矩阵如表1所示.

表1 聚类样本特征值矩阵Table 1 Characteristic value matrix of clustering samples

假设c=3,m=2,ε=10−6,δ=100.通过表1计算各特征权重,进而得到加权后的样本特征值矩阵,如表2所示.根据本工作提出的计算方法确定初始聚类中心,得到的3个聚类中心初始值分别为和再由隶属度计算公式计算初始聚类中心相应的隶属度矩阵?迭代结束?后得到?的聚类中?心为和具体如表3所示.经过2次迭代后,得到JU(1),Z(1)−JU(2),Z(2)=6.971 0×10−7＜ ε,隶属度迭代结果如表4所示.从表4可以看出,若根据最大隶属原则对样本分类,第一类为{y1,y2,y3},第二类为{y4},第三类为{y5},该结果与文献[8]和[23]中的聚类结果相同.表5为在同样考虑特征权重的前提下,本工作提出的改进算法与文献[8]和[23]中算法的比较.由表5可以看出,文献[8]和[23]中的基于直觉模糊集的聚类算法目标函数的初始值较大,迭代次数多.由以上分析可见,采用本工作提出的方法,可以极大地提高聚类性能.由于初始聚类中心有效地避开了噪声点,获得了较小的目标函数初始值,因此大大减少了迭代次数,克服了目标函数在寻优过程中易陷入局部最优值的缺陷,同时加快了收敛速度.综上可知,本工作提出的聚类算法在聚类样本数较多、样本特征权重之间差异明显的实例中,可取得更好的聚类效果.

表2 加权后的样本特征值矩阵Table 2 Weighted characteristic value matrix of clustering samples

表3 聚类中心Table 3 Clustering center

表4 隶属度矩阵Table 4 Membership matrix

表5 聚类算法结果的比较Table 5 Comparison of clustering results

4 结束语

本工作给出了一种改进的基于直觉模糊集的FCM聚类算法,该算法考虑到样本的特征权重对聚类效果的影响,利用直觉模糊熵对特征值进行加权;考虑到传统FCM聚类算法中随机选取初始聚类中心的不合理性,定义了区域密度,通过比较每个样本的区域密度,在高密度区域中选取初始聚类中心.最后通过算例验证了该聚类方法的正确性和有效性.由于算法在计算机上易于实现,可用于解决大数量以及实时性要求较高的聚类问题.需要指出的是,样本的聚类数目和加权指数的确定等还需要进一步探讨,这些问题的解决直接关系到最终聚类结果的有效性.