相邻交叉口混合交通流鲁棒多目标信号优化控制

陈 娟,余雨轩,荆 昊

(上海大学悉尼工商学院,上海201899)

我国城市交通的一个显著特点是路网中机动车、非机动车、行人等多种出行方式并存.在以往的大多数研究中,更多的是强调路网中机动车流的协调运行,而忽略了非机动车流、行人流等慢行交通的出行需求,从而导致通行权分配不合理,交通流间的冲突现象较为严重.这与城市可持续发展中倡导的绿色出行理念相违背.

混合交通流环境下的交通信号控制问题,需要从多交通效益的角度出发,综合道路使用率、出行者时间效益和环境效益,在各种出行方式的混合组成结构下,对配时参数进行优化,全面地优化交通性能指标,因此是一个典型的多目标优化控制问题.对于该问题,以往的处理方法主要有两种:一是采用线性加权的方法[1],将多目标优化或控制问题描述为单目标优化或控制问题来解决,由于加权法很难确定权值,而且无法处理非凸控制问题,因此采用该方法存在较大的风险;二是采用多目标优化或控制方法.多目标进化算法作为一种有效的多目标优化和控制方法,近年来已经越来越多地被应用于多目标交通信号控制研究中.陈小红等[2]针对各种交通方式混行的信号控制交叉口,以通行能力最大、车辆停车率及出行者平均延误最小为目标,以饱和度为约束条件,建立了交叉口信号配时多目标优化模型,并根据不同交通状态下各种交通方式的混合比例确定各性能指标的重要程度,最后运用遗传算法进行求解.肖婧等[3]提出了一种基于高维多目标进化算法的交叉口混合交通流信号智能优化控制方法,设计了基于GRMODE算法的交叉口混合交通流高维多目标信号优化控制模型,该方法能够使交叉口机动车平均延误、停车次数、通行能力、非机动车平均延误及行人等待时间等多项性能指标同时达到最优,提升了交叉口智能信号控制效率.韩印等[4]以区域路网机动车总延误为优化目标,建立了非机动车影响条件下的区域交通信号控制优化模型,优化了信号周期时长、绿信比和相位差等参数,并利用遗传算法求解模型.Yin[5]提出了3个模型来确定对交通流波动敏感的鲁棒最优信号配时,研究结果表明,即使在最差的情形下,该模型也能够在不损失很多最优性的前提下,保证一定程度的系统性能指标的鲁棒性.

目前,现有的多目标交通信号控制方法仍存在一定缺陷:一是现有的控制方法主要针对交叉口机动车流进行信号控制,较少考虑非机动车和行人的影响,无法适应实际交叉口混合交通流的信号控制需求;二是绝大多数研究都是假设交通流的动态运行环境是静止不变的,这种假设忽略了交通流变化的波动性、动态性和不确定性,导致信号控制方法难以实时适应其波动,也不能很好地分析交通流性能指标对交通参数和环境变化的敏感性.这属于鲁棒多目标优化问题,目前普遍采用单目标进化算法和带精英策略的非支配排序的遗传算法(improved non-dominated sorting genetic algorithm,NSGA-Ⅱ)等传统的多目标进化算法进行求解,存在收敛精度差、耗时和无法获取最优解等问题.

针对以上问题,本工作设计了综合机动车平均延误、道路通行能力,慢行交通平均延误,机动车平均停车率等交通性能指标的相邻交叉口鲁棒多目标信号优化控制模型.为了成功且高效地求解该模型,设计了鲁棒度非支配排序遗传算法IDR-NSGA-Ⅱ,通过对多项关键技术的改进,提升现有多目标进化算法的求解精度和运行速度,并提出了多属性决策方法进行配时方案的选择.

1 模型

针对高峰期交通信号的定时配时问题,目前绝大多数的研究是根据某段时间(比如一周)内的同一高峰期(比如早高峰,每天8:30—9:30)的平均交通流量来确定.但是,这种仅把某一固定流量作为依据的配时方法,使得配时方案对流量波动非常敏感,鲁棒性较差.因此,本工作采集多个高峰期的交通流量进行信号配时,期望获得的配时方案对于交通流波动较大的高峰期信号交叉口具有较好的鲁棒性,提升交通安全性能.

模型假设条件如下:①相邻交叉口间无机动车出入,机动车沿主干道正常行驶,无转向或停留;②相邻两交叉口之间只有一个人行横道;③两交叉口混合交通结构相当;④交叉口与人行横道均为定时控制;⑤机动车均以饱和流率驶离交叉口或人行横道;⑥不考虑机动车驶离交叉口时非机动车产生的干扰;⑦不考虑停车线前机动车排队长度对路段长度的影响.

假设交通流均匀到达交叉口,分析时段Tm包含w个高峰期,不同高峰期的交通流量值存在较大的波动.选择Tm内,相邻交叉口的机动车平均延误/道路通行能力,慢行交通平均延误,机动车平均停车率,交通流延误鲁棒优化模型(robust optimization model for traffic delay,ROMTD)为优化目标,设计如下鲁棒多目标优化控制模型:

2 算法

传统的交通信号配时多目标优化问题的研究,以获取符合决策者偏好的全局最优解为主要目的.随着研究的深入,最优解的鲁棒性的研究日益引起学者们的关注.Ide等[6]采用目标函数的期望或方差衡量解的鲁棒性,但该方法难以直观地进行解的鲁棒性控制.本工作采用鲁棒度作为解的鲁棒性衡量指标,根据目标函数值对决策变量扰动的响应情况确定解的扰动邻域,从而获得鲁棒最优解.针对鲁棒度指标计算过程中解邻域的抽样样本大小的确定问题,本工作提出了一种自适应抽样技术,降低了算法时间复杂度.

2.1 基于ALHS鲁棒度计算平均有效函数

2.1.1 平均有效函数

Deb等[7]提出采用平均有效函数获得鲁棒最优解,实现最优解和鲁棒解的折中.基于此,交通信号配时多目标鲁棒优化问题描述如下:

显然,精确的平均有效函数值依赖于抽样方法的可靠性.简单的随机抽样法较为粗糙,精度较低,因此采用拉丁超立方体抽样(Latin hypercube sampling,LHS)进行个体的邻域抽样,以提高平均效目标函数的计算精度.周期C的邻域Nδ可以视为一个超立方体

2.1.2 鲁棒度计算

Deb等[8]采用鲁棒度度量决策变量的鲁棒性,该方法以等差数列的形式固定邻域kσ的抽样规模,在一定程度上保证了求解的准确度,但是也增加了计算的工作量.本工作提出一种自适应拉丁超立方体抽样(adaptive LHS,ALHS)方法,在计算过程中自适应调整样本大小.该方法的基本思想为:解X的邻域kσ,其两次抽样获得的目标函数值属于f(X)邻域η的百分比间的误差小于规定的精度µ,则返回较小的样本数Sk及其对应的百分比Pk.

步骤2 采用LHS进行抽样,计算样本对应的目标函数值,属于f(X)邻域η的百分比令是第m次抽样获得的样本数.

步骤3 采用LHS进行抽样,计算样本对应的目标函数值,属于f(X)邻域η的百分比是第m次抽样获得的目标函数值属于f(X)邻域η的百分比.

基于ALHS算法计算改进后的鲁棒度,具体方法如下.

步骤1 初始化Q,δ,Hmin,Hmax,令k=1.

步骤2 应用算法,获得解X,当前k的样本数Sk及其对应的百分比Pk.

步骤3 当k=1时,转到步骤4,否则,判断Pk＜Q是否成立.若成立,令解X的鲁棒度k=k−1,返回对应样本数Sk,结束程序;

步骤4 令k=k+1,转到步骤2.

基于ALHS计算鲁棒度的方法,能够根据解X的鲁棒度k自适应确定其扰动邻域及抽样大小Sk.相对于固定样本规模的抽样方法,该方法可减少的总样本规模为采用多目标优化算法求解平均有效函数时,进化代数为G,种群规模为N,可减少的总样本规模为其中Si,j,k为第i代种群中第j个个体(解)采用ALHS-DR(ALHS degree of robust)算法在邻域kσ的样本规模,则为相应的固定样本规模.

2.2 基于鲁棒度的NSGA-Ⅱ算法

本工作对NSGA-Ⅱ[9]进行改进,提出了IDR-NSGA-Ⅱ,该算法将鲁棒度融入进化过程中,获得相应的鲁棒Pareto前沿,主要措施如下:采用鲁棒度衡量解的鲁棒性,应用鲁棒度初步确定个体的扰动邻域范围和参与平均目标函数计算的样本规模;建立鲁棒外部种群,确保鲁棒精英解进入下一代进化流程;将基于鲁棒度改进的偏序关系,作为构建新种群的参考依据;基于鲁棒度设计选择算子,参与评价个体适应度值.

(1)鲁棒外部种群.通过建立外部种群存放每代进化中获得的鲁棒解,引导进化流程,搜索到期待的鲁棒解.鲁棒外部种群选择个体时,首先选择鲁棒度较大者.若鲁棒度相同,则根据非支配排序选取优者,非支配排序较小的更优;若个体鲁棒度及非支配排序均相同,则比较拥挤距离,取拥挤距离较大者.依次类推,直至外部种群数到达最大.

(2)鲁棒偏序关系.对文献[7]中的偏序关系进行改进,定义如下鲁棒偏序关系:

式中,ir1表示个体i的非支配序,ir表示个体i的鲁棒度,id表示个体i拥挤聚集度.从该鲁棒偏序关系可以看出,当两个个体非支配序不同时,非支配序小的个体占优;当两个个体非支配序相同时,鲁棒度较大的个体占优;当两个个体的非支配序和鲁棒度均相同时,拥挤聚集较大的个体占优.

(3)基于鲁棒度的选择机制.多目标遗传算法中,选择算子为搜索最优解指定方向.本工作基于鲁棒度提出如下选择方法:在种群选择任意两个个体时,首先比较个体的非支配排序,排序较小者更优;若非支配排序相同,则比较个体的鲁棒度,鲁棒度较大者更优;若个体的非支配排序和鲁棒度均相同,则进行拥挤距离比较,取拥挤距离较小的解作为最优解.

3 基于极限学习机(extreme learning machine,ELM)的多属性智能决策分析

采用IDR-NSGA-Ⅱ求解ROMTD,获得候选信号配时方案集.从候选信号配时方案集中选择最优配时方案,属于多属性决策问题.考虑到实际问题中存在的不确定性,偏好信息往往呈现出复杂的非线性关系,很难建立线性模型直接描述决策者的偏好函数.因此,提出新的决策方法ELM-MADMA(ELM multi-attribute decision making analysis).首先采用文献[10]中提出的主客观信息偏差最小法(minimum deviation analysis for subjective and objective information,MDASOI)获取或构造决策者的偏好结构信息,完成候选方案的排序,然后采用ELM算法[11]进行非线性回归,获得最优配时方案.

多属性决策的实质是利用已有的决策信息,通过一定的方式对一组备选方案进行排序,其实质是模式匹配的数学映射问题.设置配时方案Mi的属性值向量(xi1,xi2,···,xin)作为输入,决策者对方案Mi的效用评价ui作为输出,首先采用文献[10]中的MDASOI法获得方案贴近度作为效用评价值,然后建立基于ELM的决策模型,得到逼近F的非线性映射即将决策方案作为ELM的输入向量,效用评价值ui作为ELM的目标值,构造学习样本集建立ELM回归模型.

ELM-MADMA决策方法分为学习阶段和执行阶段.学习阶段由构造学习样本、训练和测试3个阶段构成,其中学习样本一般反映决策者的偏好信息,采用MDASOI方法兼顾决策矩阵的客观信息.将学习样本分为训练集和测试集,通过对训练集的学习,由ELM方法建立决策模型,并由测试集检验该决策模型.学习阶段完成后,ELM存储了决策者的决策经验、知识、主观判断以及对不同评价指标的重要性看法等偏好信息和信息推理机制.执行阶段则根据学习阶段建立的决策模型完成候选方案的排序或选择.此时,决策者的偏好信息可通过ELM来体现,从而不需要进行评价指标权重确定、确定排序方法等,就可以对决策问题做出快速合理的判断,得到最优方案.

4 实例分析

4.1 基础数据

选取上海市天目西路与恒丰路交叉口(交叉口1)、天目西路与民立路交叉口(交叉口2)作为研究对象,进行数值分析.该路段高峰期交通负荷较大,且由于临近上海火车站,交通流波动较大,对信号配时方案的鲁棒性需求较高.相领交叉口的几何构型如图1所示.

实测获得两个交叉口一周内早高峰期(早上8:30—9:30)的交通流数据,为使信号配时方案适应尽量大的交通流波动,选取交通流量差最大的2个高峰期数据进行研究,具体数据如表1所示.基于表1,采用四相位机制对交叉口1和交叉口2进行信号协调控制,建立ROMTD模型,设定周期时长约束为62≤C≤160,各相位最小绿灯时间5 s,损失时间为10 s.应用IDR-NSGA-Ⅱ求解上述模型,获得候选信号配时方案集,其中算法参数设置如下:种群规模200,鲁棒外部种群规模33,最大进化代数300,交叉概率0.95,变异概率0.05,周期扰动邻域5≤kδ≤30,δ=5,鲁棒度k∈{1,2,3,4,5,6},指定百分比参数Q=0.75,目标函数邻域η={0.5,0.5,0.5}.

4.2 鲁棒优化

采用IDR-NSGA-Ⅱ获得相应的鲁棒Pareto前沿,结果如图2所示.由图2可知:机动车平均延误/道路通行能力,慢行交通平均延误以及机动车平均停车率,三者之间彼此冲突;随着ROMTD值的增大,机动车平均停车率随之降低,二者存在明显的冲突关系.

4.3 智能决策

智能决策方法ELM-MADMA的参数设置如下:定义道路通行能力和解的鲁棒度为效益型指标,机动车平均停车率及慢行交通平均延误定义为成本型指标,机动车平均延误为区间型指标,机动车平均延误的最佳区间是[25.0,28.0].建立200组配时方案作为学习样本,随机选取180组数据作为训练集,剩余20组作为测试集.ELM核函数为sigmoid函数,隐含层个数为75.

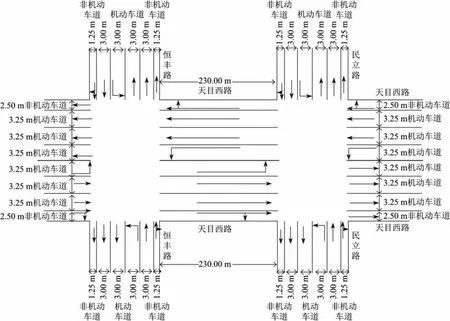
图1 相邻交叉口的几何构型Fig.1 Geometry structure of the adjacent junction

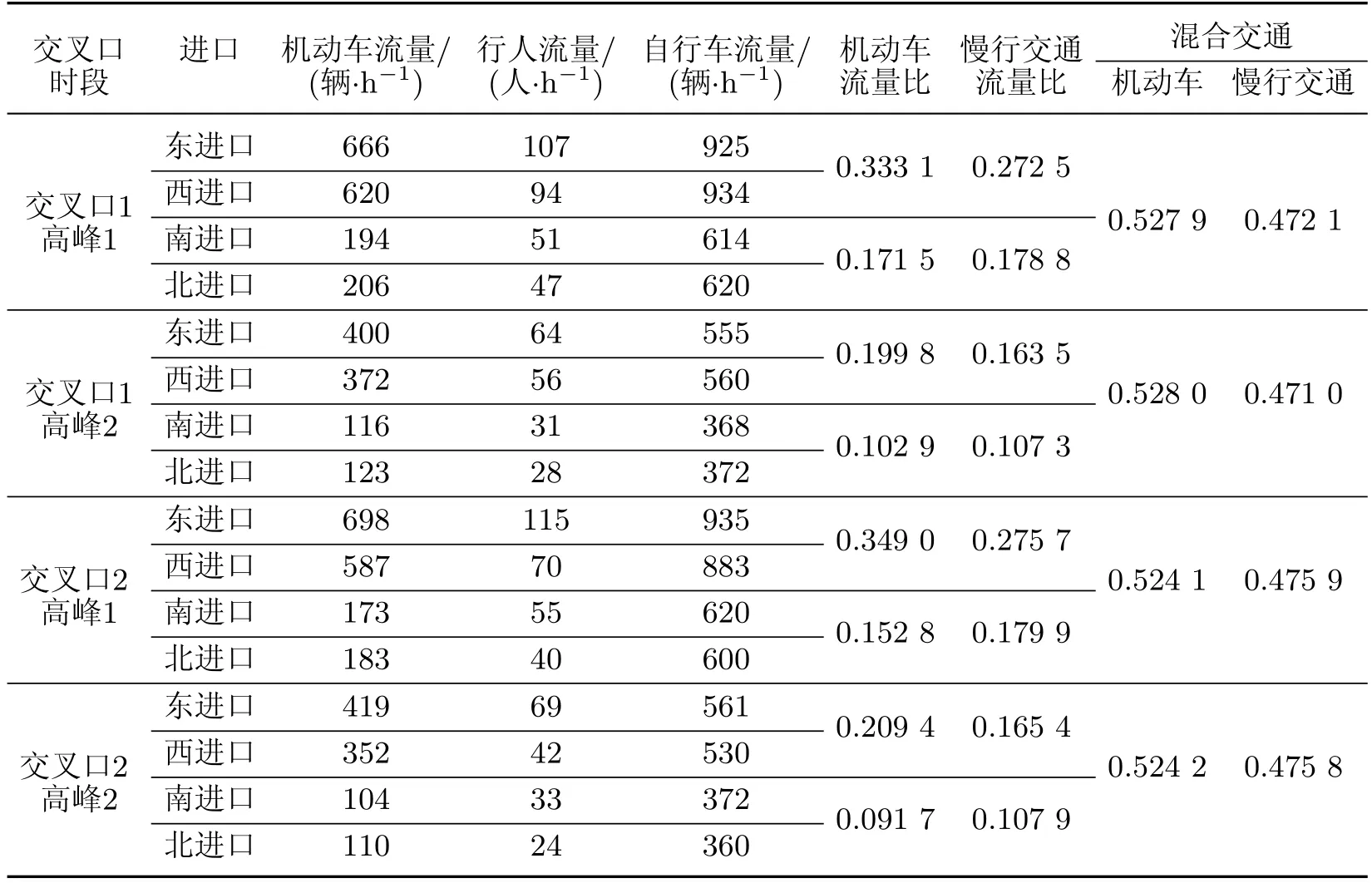
表1 相邻交叉口的高峰期交通流量Table 1 Traffic f l ow of the adjacent junction

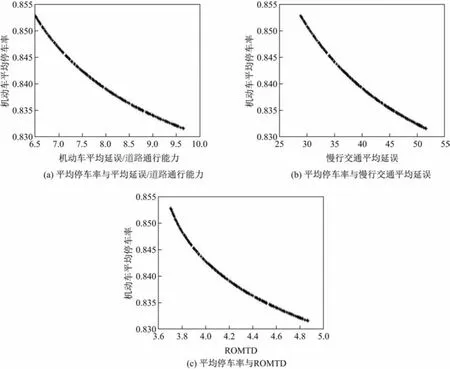
图2 Pareto前沿结果Fig.2 Result of the Pareto front

表2中给出了基于BP神经网络(back propagate neruon network,BPNN)、支持向量机(support vector machine,SVM)和超限学习机(extreme learning machine,ELM)的智能决策法对相同配时方案集M 进行排序的回归分析结果.由表2可知:ELM-MADMA的测试集均方误差(mean-square error,MSE),远低于BPNN-MADMA和SVM-MADMA,表明ELM-MADMA的输出效用评价者值和期望评价值间差异最小,ELM-MADMA更好地学习了评价效用决策信息;ELM-MADMA所得非线性回归模型的方程确定性系数R2最大且更接近1,进一步表明本工作采用交通性能评价指标基本上完全解释了决策者期望的效用评价,采用ELM-MADMA进行信号配时决策分析具有一定的应用前景;ELM-MADMA的运行时间也远低于BPNN-MADMA和SVM-MADMA,表明ELM-MADMA算法可有效地提升决策效率.综上可知,ELM-MADMA的决策效果最好.

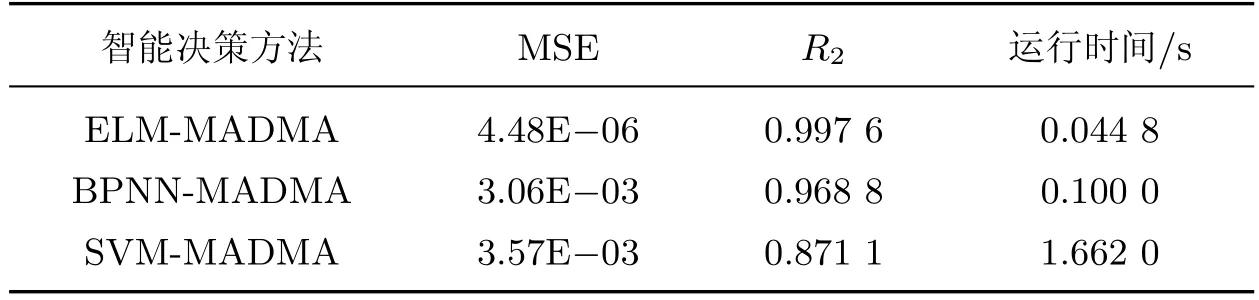
表2 不同智能决策方法的对比结果Table 2 Result of different intelligent decision making methods

4.4 性能指标

基于图1和表1,利用VISSIM软件搭建交通路网,并完成各个进道口的交通流量输入,然后将ELM-MADMA法获得的配时方案输入VISSIM仿真系统.表3给出了不同信号配时法下相邻交叉口系统的性能指标.由表3可知,与高峰期2相比,高峰期1的交叉口交通流饱和度更高.与文献[12]中的单点控制方法相比,本工作中的方法能够有效地降低高峰期1的平均行驶时间.在交叉口1到交叉口2的路段上,利用本工作提出的方法得到平均行驶时间是117.931 7 s,比文献[12]中的方法减少了56.85%,机动车平均延误降低了17.12%,慢行交通平均延误和机动车平均停车率分别降低了0.75%和1.8%.

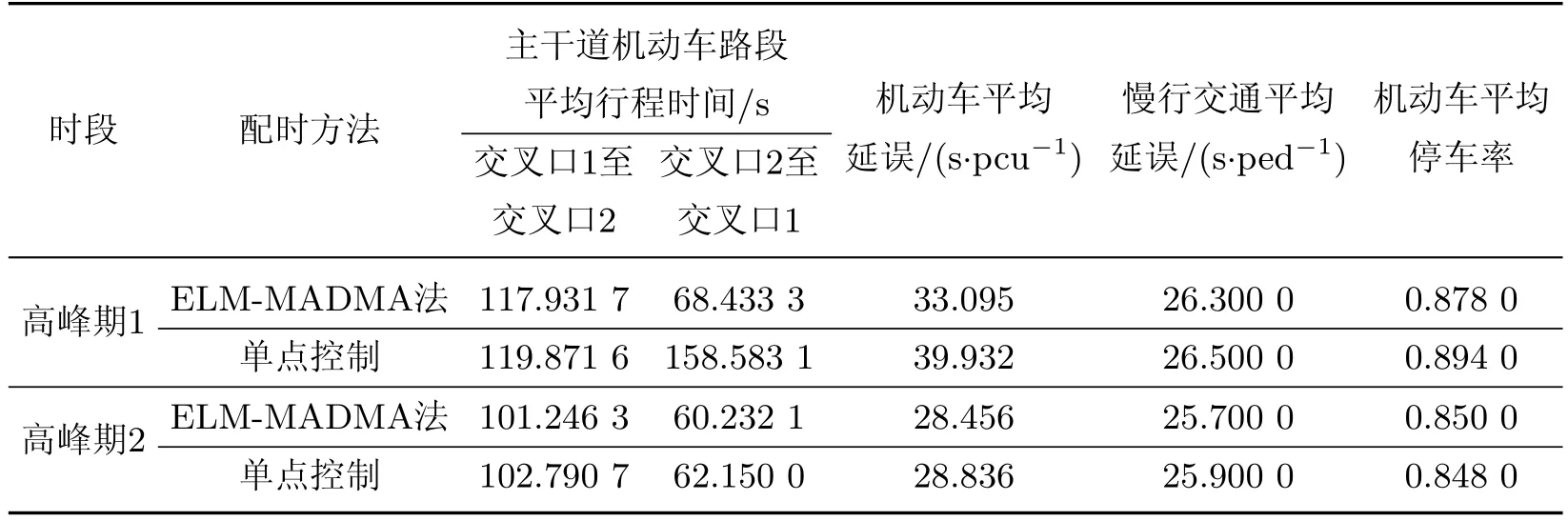
表3 信号配时方法不同时的性能指标Table 3 Result of different intelligent decision making methods

5 结束语

针对我国城市道路相邻交叉口在混合交通流环境下信号控制中的不确定性和效率问题,提出一种基于鲁棒多目标进化算法IDR-NSGA-Ⅱ的智能优化控制方法,进行了周期时长扰动和交通流波动下机动车平均延误,道路通行能力,慢行交通平均延误,机动车平均停车率多项性能指标的最优化控制.为了高效求解基于鲁棒模型的多目标优化控制问题,提出了新的鲁棒多目标优化算法,包括自适应抽样技术、鲁棒度定义、鲁棒偏序关系定义等多项关键技术,同时提出新的多属性决策方法ELM-MADMA选择配时方案.克服了国内外现有算法求解精度低、计算耗时大、不适用于实际工程优化的缺陷.仿真实验的结果表明,本工作提出的算法能够有效地提升相邻交叉口混合交通流高峰小时流量水平下的智能控制效率,具有较短的运行时间,为智能交通系统的开发和研究提供了必要的理论支持.